Item C sold half as many times as item D. Altogether, you sold 54 of these items. How many of items C did you sell today? How many of items D did you sell?

Answer:

8, 1, and 3

Step-by-step explanation:

Range is the y in (x, y)

Hope it helps

The solution for x in the equation is x = 4/7

from the question, we have the following parameters that can be used in our computation:

-x + 3/7= x - 5/7

Collect the like terms

So, we have

2x = 8/7

Divide both sides of the equation by 2

So, we have

x = 4/7

Hence, the solution is x = 4/7

Read more about equation at

https://brainly.com/question/32583193

#SPJ1

Answer:

The difference between the maximum and the minimum temperature on that day is \(18^0C\)

Step-by-step explanation:

The maximum temperature of an island was recorded \(15.5^0C\)

The minimum temperature was recorded \(-2.5^0C\)

Difference in temperature

\(=15.5--2.5\\\\=18^0C\)

Answer:

the difference between 15.5 and -2.5 is 18

Step-by-step explanation:

You didn't include a picture/ diagram

Answer:

B. 4^13

C. -1/64

Step-by-step explanation:

Answer:

B. \(4^{13}\)

C -1/64

Step-by-step explanation:

7. \((4^{4} )^{3} (4)(3^{0} )=(4)^{12} (4)(1)=4^{13}\)

8. \(-(4)^{4} (4)^{-7} =-(4)^{-3} =-\frac{1}{4^{3} } =-\frac{1}{64}\)

Hope this helps

The correct answer is A) 16. It would take 16 hours to fill the container if 5/8 of a gallon is added each hour.

If 5/8 of a gallon is added to the container each hour, we can calculate the number of hours it would take to fill the container.

Let's assume it takes "h" hours to fill the container. In each hour, 5/8 of a gallon is added. Therefore, in h hours, the total amount of water added would be (5/8) * h gallons.

According to the problem, the container holds 10 gallons of water. So, we can set up the equation:

(5/8) * h = 10

To solve for h, we can multiply both sides of the equation by 8/5:

h = 10 * (8/5)

h = 16

for more such questions on equation

https://brainly.com/question/22688504

#SPJ8

The probability of randomly selecting a red marble from the jar is 1/4 or 0.25 (25%).

The probability of randomly selecting a red marble from the jar can be calculated by dividing the number of red marbles by the total number of marbles in the jar. In this case, there are 10 red marbles and 30 blue marbles, so the total number of marbles is 40. Therefore, the probability of selecting a red marble is 10/40 or simplified to 1/4. This means that there is a 25% chance of selecting a red marble from the jar at random. The answer to your second question is 10/30, 10/40, 1/10, and 1/40 are all potential answer choices, but the correct answer is 1/4.

A jar contains 10 red marbles and 30 blue marbles, making a total of 40 marbles in the jar. To find the probability of randomly selecting a red marble from the jar, you need to divide the number of red marbles by the total number of marbles.

The probability of selecting a red marble is:

(10 red marbles) / (40 total marbles) = 10/40

Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 10:

10/40 = 1/4

So, the probability of randomly selecting a red marble from the jar is 1/4 or 0.25 (25%).

Learn more about probability at: brainly.com/question/30034780

#SPJ11

Answer:

Step-by-step explanation:

from the angles we understand that it is an isosceles right triangle, therefore x is also 13, we find y with the Pythagorean theorem

y = √(13² + 13²)

y = √(169 + 169)

y = √338

y = 18.38 (you can round to 18.4)

Answer:

x = 13 , y = 18.38

Step-by-step explanation:

p.s. There is two ways to answer it.

In Triangle,

if there is a right angle, other angles are the same.

It the angles are the same, the two sides are the same.

So, x = 13

By the Converse of the Pythagorean Theorem , these values make the triangle a right triangle.

(hypotenuse)² = (side of right triangle)² + (other side of right triangle)²

(hypotenuse)² = 13² + 13²

(hypotenuse)² = 169 + 169

(hypotenuse)² = 338

hypotenuse = 18.38

so y = 18.38

Answer:

a7=-1

Step-by-step explanation:

Arithmetic Sequences

The arithmetic sequences can be identified because each term n is obtained by adding or subtracting a fixed number to the previous term n-1.

The equation to calculate the nth term of an arithmetic sequence is:

\(a_n=a_1+(n-1)r\)

We know: a12=29, a16=53, now we use the above equation for n=12 and n=16:

\(a_1+(12-1)r=29\)

\(a_1+(16-1)r=53\)

Simplifying both equations:

\(a_1+11r=29\)

\(a_1+15r=53\)

Subtracting:

\(4r=53-29=24\)

Solving:

r=24/4

r=6

The 7th term can be found as 9 terms before the 16th:

\(a_7=a_{16}-9r\)

\(a_7=53-9*6=53-54=-1\)

Thus: a7=-1

Answer:

3/2

Step-by-step explanation:

"Negative" means take the opposite sign.

"reciprocal" means flip it over.

Answer:

\(\left(ab^2x-b^4a^3\right)^2:\quad a^2b^4x^2-2a^4b^6x+a^6b^8\)

Step-by-step explanation:

Given the expression

\(\left(ab^2\:x\:-b^4a^3\right)^2\)

solving the expression

\(\left(ab^2\:x\:-b^4a^3\right)^2\)

\(\mathrm{Apply\:Perfect\:Square\:Formula}:\quad \left(a-b\right)^2=a^2-2ab+b^2\)

\(a=ab^2x,\:\:b=b^4a^3\)

so the expression becomes

\(=\left(ab^2x\right)^2-2ab^2xb^4a^3+\left(b^4a^3\right)^2\)

\(=a^2b^4x^2-2a^4b^6x+a^6b^8\)

Thus,

\(\left(ab^2x-b^4a^3\right)^2:\quad a^2b^4x^2-2a^4b^6x+a^6b^8\)

The price that would yield maximum revenue is $260  and maximum revenue is $1,690,000

What is the revenue function?

The fact that total revenue of  the company is the price per purse multiplied by the number of purses sold, means that the revenue modelled function is simply price multiplied by the quantity sold as shown below:

R(x)=P*x

R(x)=Px

R(3000)=$400*3,000

R(3000)=$1200,000

Note for every 500 more purses, the price reduces by $20

R(3500)=$380*3,500

R(3500)=$1,330,000

R(4000)=$360*4000

R(4000)=$1,440,000

R(4500)=$340*4500

R(4500)=$1,530,000

R(5000)=$320*5000

R(5000)=$1,600,000

R(5500)=$300*5500

R(5500)=$1,650,000

R(6000)=$280*6000

R(6000)=$1680,000

R(6500)=$260*6500

R(6500)=$1,690,000

R(7000)=$240*7000

R(7000)=$1,680,000

The total revenue fell at 7,000 purses, which means that the maximum revenue is $1,690,000 at 6500 purses

Find out more about revenue on:brainly.com/question/14305184

#SPJ1

Answer:

AB = A'B'

BC = B'C'

AC = A'C'

angle ABC = angle A'B'C'

angle CAB = angle C'A'B'

angle CBA = angle C'A'B'

Step-by-step explanation:

use different axomes to show relation,

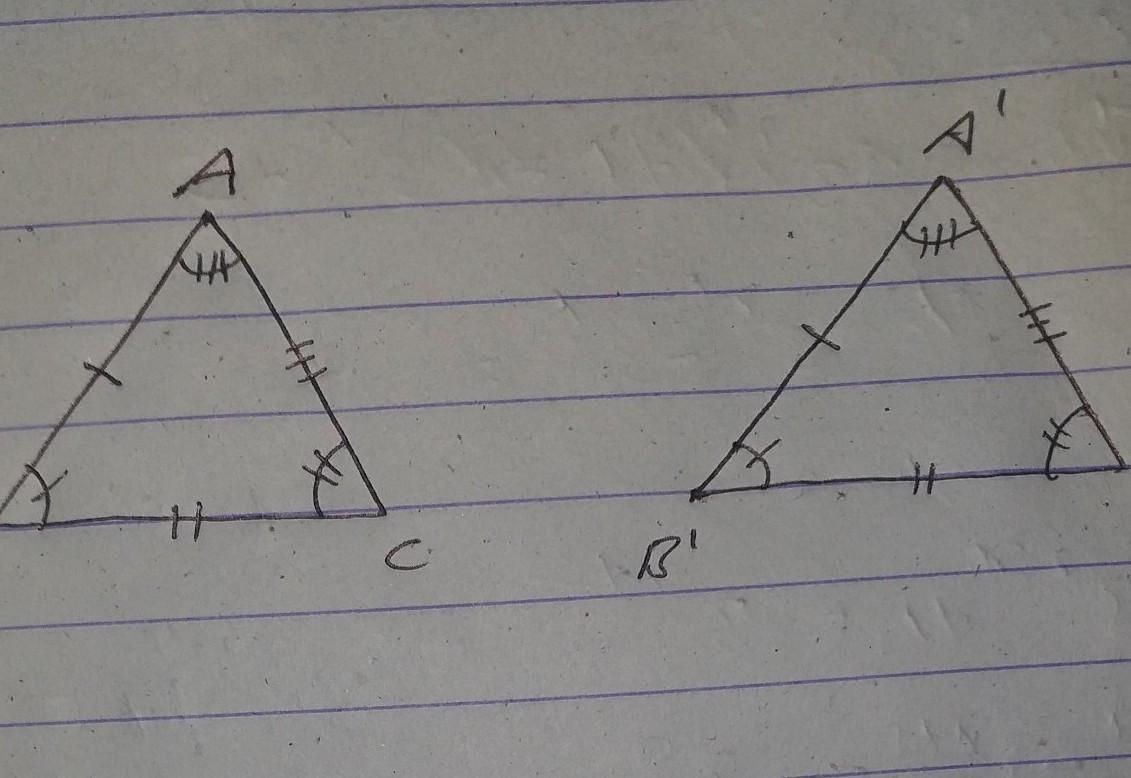
Answer: Reflect ABC across the vertical line passing through C

Step-by-step explanation:

given :- tanA=4/3

we already know that tanA=P/B

From Pythagorean theorem we get..

H²=P²+B²

H²=4²+3²

H²=16+9

H²=25

H²=5²

H=5

SinA=P/H

CosA=B/H

from that

SinA= 4/5

CosA=3/5

In this context, the dependent variable is t (amount of tax due) and the independent variable is c (cost of the order).In this scenario, the variables are t (the amount of tax due) and c (the cost of the order).

To determine which variable is independent and which is dependent, we need to understand their relationship.In this case, the amount of tax due, t, is calculated based on the cost of the customer's order, c. The tax amount is dependent on the cost of the order because it is directly influenced by the value of c. As the cost of the order changes, the amount of tax due will also change accordingly.

On the other hand, the cost of the order, c, is independent. It is not influenced or determined by the amount of tax due. The customer can choose the cost of their order, and the tax will be calculated based on that chosen amount.

For more such questions on variable

https://brainly.com/question/27894163

#SPJ8

Answer: 4bx^2

Step-by-step explanation:

Answer:

Hey there!

I got the answer

4bx^4

Step-by-step explanation:

All you have to do is simplify the radicand up into a product of known factors , assuming positive real numbers.

Answer: Just time 2 x 73 and you will get 146

Step-by-step explanation:

The segment UV = 22 1/4 inches, using the segment addition postulate.

According to the segment addition postulate, a third point B will only be located on the line segment AC if and only if the equation AB + BC = AC is true for a line segment with two endpoints, A and C.

In the question, we are given that point W bisects segment UV.

We are asked to find UV if WV = 11 1/8 inches.

For the segment UV, if point W bisects it, then point W is on the segment, and by the segment addition postulate, we can write that UW + WV = UV.

Now, as we are given that W bisects UV, we can conclude that UW will be equal to WV.

Thus, we can write that UW = WV = 11 1/8 inches.

Substituting the values of UW and WV in the equation UW + WV = UV, we get:

11 1/8 + 11 1/8 = UV,

or, UV = 11 1/8 + 11 1/8,

or, UV = 89/8 + 89/8,

or, UV = 178/8,

or, UV = 89/4,

or, UV = 22 1/4.

Thus, the segment UV = 22 1/4 inches, using the segment addition postulate.

Learn more about the segment addition postulate at

https://brainly.com/question/2134445

#SPJ9

Yes, the quadratic function f(x) and the linear function g(x) will intersect. The x-coordinate of the point of intersection could be positive, negative or zero, depending on the specific functions.

From the data given, it's not possible to determine the x-coordinate of the point of intersection.

A quadratic polynomial in mathematics is a polynomial of degree two in one or more variables. The polynomial function defined by a quadratic polynomial is known as a quadratic function.

Linear functions are usually written as y = mx + b and graphed as straight lines.

Begin with the y-intercept or b value, then use the slope to identify a second point on the graph. Quadratic functions are graphed as curved parabolas and have the formula y = ax2 + bx + c.

For more questions on quadratic function

https://brainly.com/question/24737967

#SPJ4

Answer:

d=8

Step-by-step explanation:

Okay we've got 68/17 and d/2

68/17 = 4 meaning d/2 is also 4. Since 4 × 2 is 8, we know the answer is 8.

The length of the shorter leg is 16 units which was found using the given data.

A quadratic equation is a second-degree algebraic equation in x. In its usual form, the quadratic equation is ax² + bx + c = 0.

Given: The larger leg of a right triangle is twice more than three times the shorter leg, and the triangle's area is 400.

We know that,

Area of triangle = 1/2(larger leg)(shorter leg)

                  400=1/2(larger leg)(shorter leg)   Equation(1)

larger leg = 2 + 3(shorter leg)

We need to substitute this in Equation(1)

400 = 1/2[2+3(shorter leg)](shorter leg)

800 = 2(shorter leg) + 3(shorter leg)²

3(shorter leg)² + 2(shorter leg) - 800 = 0

Solving this quadratic equation,

we get, shorter leg = - 16 or +16

Thus, we found that the length of the shorter leg is 16 units as -16 cannot be the length because it is negative.

Learn more about quadratic equation here:

https://brainly.com/question/1214333

#SPJ4

Answer:

U did not add a picture but if u do I will help.

Step-by-step explanation:

It should be 8 to the right and 12 to the left which should end at -4

Answer:

The answer is 4?? tell me if it's wrong or not.

Answer:

D.

Step-by-step explanation:

So first you need to find the circumference.

22π ≈ 69.08

3600 ÷ 69.08 = 52.1134916039

Closest = D.

Answer:

a) 8cm

b) 19.8cm

Step-by-step explanation:

The key to these types of questions is to keep proportions in mind.

To solve the first question, you want to find the proportion of the smaller triangle to the bigger triangle. The length of AE is 6cm, but the length of AD is (6+4) = 10cm. So the proportion of the bigger triangle to the smaller triangle is 10/6. So to find the lengths of the sides of the bigger triangle, we want to keep this number in mind.

The BE side is parallel to CD, so we have to use length of BE multiplied by the proportion in order to get the length of CD.

CD = 4.8 * (10/6) = 8

CD = 8cm

For the second question, you use the same concept to find all the other side lengths. The only one you need left for the shape EBCD is side BC. Do the same thing you did before, take the length of the side of the smaller triangle that corresponds with side AC on the bigger triangle. In this case, it's AB, which is 4.5cm. Multiply this by 10/6 to get AC.

AC = 4.5 * (10/6) = 7.5

AC = 7.5

But we're not done. We just found the length of AC, but we need the length of BC to calculate the perimeter. To do this, we want to take the length of AC - the length of AB.

7.5 - 4.5 = 3

So the length of BC is 3cm. Now, to find the perimeter, just add all the sides of EBCD together.

4.8 + 4 + 8 + 3 = 19.8cm.

Hope this helps.

Answer:

a) CD = 8 cm

b) Perimeter of EBCD is 19.8 centimeters

Step-by-step explanation:

For this question, you can assume that ΔABE and ΔACD are similar. That's proven by BE ║ CD, but that's not directly relevant to the question so I won't explain it unless you would like me to.

In 2 similar triangles, all corresponding angles are congruent and all corresponding sides have the same scale factor.

For example, in ΔABC and ΔXYZ:

\(\frac{AB}{XY} =\frac{AC}{XZ} =\frac{BC}{YZ}\)

Using those relationships, you can solve for any side in one triangle given the corresponding side in the other triangle.

A)

In the given triangles ΔABE and ΔACD, CD corresponds to BE, so:

\(\frac{CD}{BE} =\frac{AD}{AE}\)

where AD is just 6 + 4 = 10.

\(\frac{CD}{4.8} =\frac{10}{6} \\\\\frac{CD}{4.8} =1.6667\\\\CD=8\)

CD = 8cm

B)

Doing the same thing as above, now find the length of AC:

\(\frac{AC}{AB} =\frac{AD}{AE} \\\\\frac{AC}{4.5} =\frac{10}{6}\\\\\frac{AC}{4.5} =1.6667\\\\AC=7.5\)

Now, to find BC:

\(BC=AC-AB\\BC=7.5-4.5\\BC=3\)

Finally, add up the sides to find the perimeter of EBCD:

\(4.8+3+8+4\\19.8\)

Perimeter of EBCD is 19.8 centimeters

The independent set in a graph is a set of vertices that contain no edges. So, no neighboring vertices are included. The max independent set problem is to get an independent set of maximum size in graph G.

The solution for this question is discussed below:

a) The integer linear program for the max independent set problem is as follows:

maximize ∑x_i Subject to: x_i+x_j ≤ 1 {i,j} ∈ E;x_i ∈ {0, 1} ∀i. The variable x_i can represent whether the ith vertex is in the independent set. It can take on two values, either 0 or 1.

b) The LP relaxation for the max independent set problem is as follows:

Maximize ∑x_iSubject to:

xi+xj ≤ 1 ∀ {i, j} ∈ E;xi ≥ 0 ∀i. The variable xi can take on fractional values in the LP relaxation.

c) The family of graphs is as follows:

Consider a family of graphs G = (V, E) defined as follows. The vertex set V has n = 2^k vertices, where k is a positive integer. The set of edges E is defined as {uv:u, v ∈ {0, 1}^k and u≠v and u, v differ in precisely one coordinate}. It can be shown that the size of the max independent set is n/2. Using LP, the value can be determined. LP provides a value of approximately n/4. Therefore, the ratio LP-OPT/OPT is at least c/4. Therefore, the ratio is in for a constant c>0.

d) The size of a max-independent set is equivalent to the number of vertices minus the minimum vertex cover size.

e) The 2-approximation algorithm for vertex cover implies a 2-approximation algorithm for the max independent set.

To know more about the independent set, visit:

brainly.com/question/31418821

#SPJ11

Answer:

b=12.2-8

b=4.2

thus

4.2+8=12.2

Answer:  B=4.2

Step-by-step explanation:

b+8=12.2

Subtract 8 from both sides

b+8-8= 12.2 - 8

Simplify

b=4.2

Answer:

Step-by-step explanation:

Given

Find \(a_{43}\)

We know that

Appy this to the two known terms and find the first term and the common difference

Find the coomon difference

Find the first term

Now find the 43th term

Answer:

-98

Step-by-step explanation:

General form of an arithmetic sequence:

  \(a_n=a+(n-1)d\)

where:

Given:

To find the 43rd term we need to construct an equation for the nth term.  To do this, find the first term and the common difference by substituting the given information into the general formula to create a system of equations that can be solved.

\(\begin{aligned} \underline{\textsf{Equation 1}}} \\ a_{21} & =-32 \\ \implies a+(20-1)d & = -32 \\a+20d & =-32 \end{aligned}\)

\(\begin{aligned} \underline{\textsf{Equation 2}}} \\ a_{50} & =-119 \\ \implies a+(50-1)d & = -119 \\a+49d & =-119 \end{aligned}\)

Subtract Equation 1 from Equation 2 to eliminate a:

\(\begin{array}{r l}a+49d & = -119\\- \quad a+20d & = -32\\\cline{1-2}29d & = -87\end{aligned}\)

Solve for d:

\(\implies d=\dfrac{-87}{29}=-3\)

Substitute the found value of d into one of the equations and solve for a:

\(\implies a + 20(-3)=-32\)

\(\implies a=28\)

Substitute the found values of a and d into the general formula to create an equation for the nth term:

\(\implies a_n=28+(n-1)(-3)\)

\(\implies a_n=31-3n\)

Finally, substitute n = 43 into the found formula to find the 43rd term of the sequence:

\(\implies a_{43}=31-3(43)=-98\)

Learn more about arithmetic sequences here:

https://brainly.com/question/27806372

https://brainly.com/question/27783089

Answer:

40

Step-by-step explanation:

-50 + 90 = 40

Solution

We will