in the context of the measures of reliability, correlating the total score of the first 20 questions on a test with the total score of the last 20 questions on a test is an example of
Answers
In the context of measures of reliability, correlating the total score of the first 20 questions on a test with the total score of the last 20 questions on the same test is an example of test-retest reliability.
Test-retest reliability is a measure of the consistency of test scores over time. It assesses the degree to which test scores are consistent when the same test is administered twice to the same group of individuals at different times.
In the example given, the first total score represents the results of the first administration of the test, while the second total score represents the results of the second administration of the test. By correlating the two scores, we can assess the degree of consistency between the two sets of scores and determine the test-retest reliability of the test.
If the correlation between the two total scores is high, it indicates that the test is reliable and produces consistent results over time. If the correlation is low, it suggests that the test may not be reliable and that the results may be subject to random variation or measurement error.
Learn more about "Test-retest reliability" : https://brainly.com/question/13860893
#SPJ11
Related Questions
(-5, -4) and (-13,2)
Answers
The slope of the line passing through the points (-5, -4) and (-13, 2) is -3/4.
What is the slope of the line through the given points?Slope is simply expressed as a change in y over the change in x.
It is expressed as
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
Given the points:
(-5, -4) and (-13,2)
Point (-5, -4):
x₁ = -5
y₁ = -4
Point (-13,2):
x₂ = -13
y₂ = 2
Plug the given x and y values into the slope formula and simplify.
\(m = \frac{y_2 - y_1}{x_2 - x_1}\\\\m = \frac{2 - (-4)}{-13 - (-5)}\\\\m = \frac{2 + 4}{-13 + 5}\\\\m = \frac{6}{-8}\\\\m = -\frac{3}{4}\)
Therefore, the slope of the line is -3/4.
Learn more about slope formula here: brainly.com/question/24578307
#SPJ1
AB=CD what is the property
Answers
Find the quotient for the following problems.
16/224=
38/792=
42/504=
47/5,170=
58/7,211=
Answers
Answer:
14,20.84,12,110,124.32
Help! I’ll mark brainly list
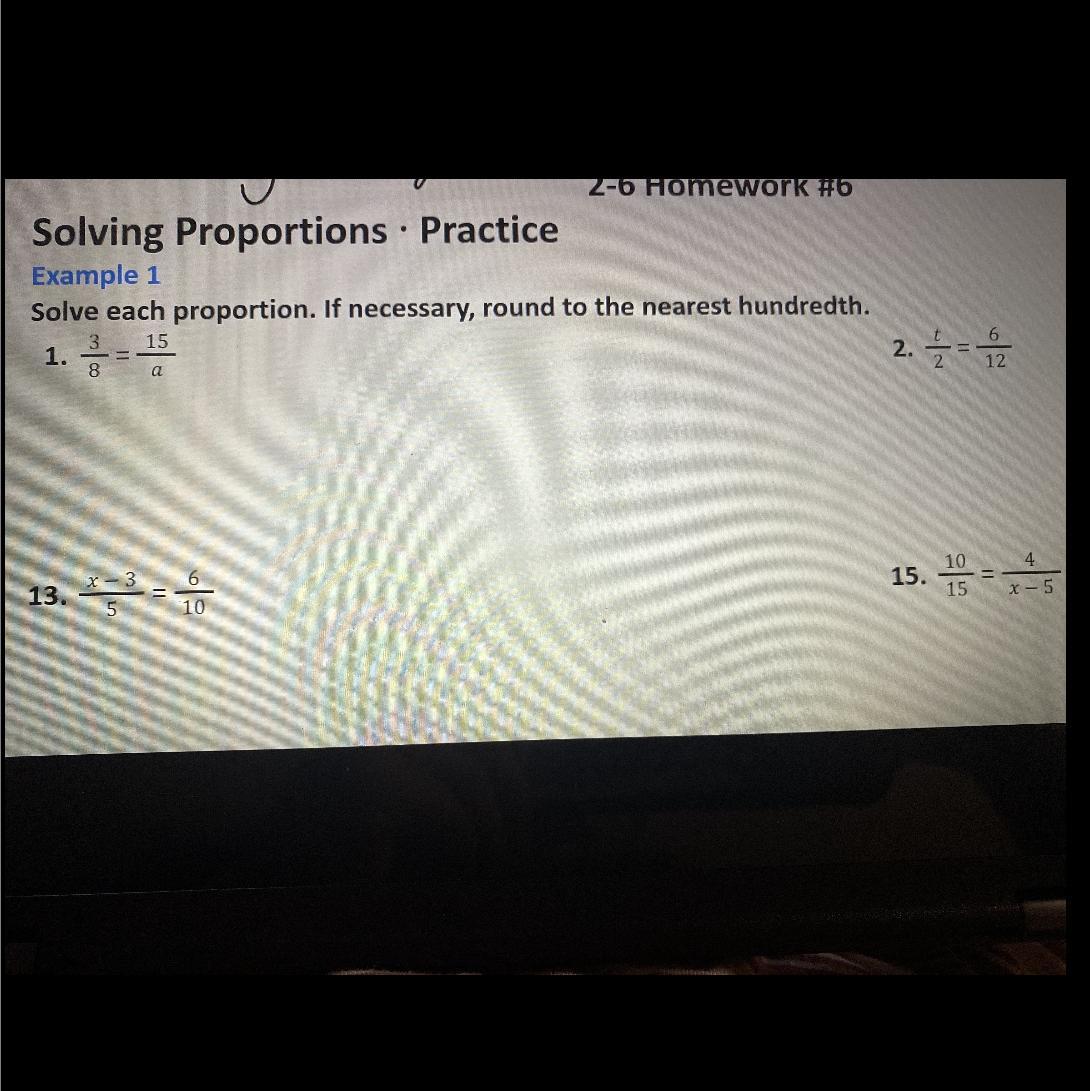
Answers
Answer:
a = 40
t = 1
x = 6
x = 11
Step-by-step explanation:
1.
3/8 = 15/a
multiply both sides by a, then multiply by the reciprocal of 3/8
a = 8*15/3
2.
multiply both sides by 2
t = 1
3.
multiply both sides by 5
x - 3 = 30/10
x = 6
4.
multiply both sides by x - 5, then multiply by the reciprocal of 10/15
60/10 = x - 5
x = 6
Tawny wrote an expression to represent "the quotient of 82 and a number, decreased by 26." She then evaluated the expression when n = 2. Which statements are true about the expression and its value? Check all that apply.
Answers
Answer:
D, E, G
Step-by-step explanation:
Quotient of 82 and a number=82/n
Decreased by 26
82/n-26
She evaluate the expression when n=2
82/n-26
When n=2
82/2-26
=41-26
=15
Answer
D. The correct expression is 82/n-26
E.The operations include division and subtraction.
G.The value of the expression is 15
Answer:
The correct answer is b,d,e,g
Step-by-step explanation:

The hypotenuse of an isosceles right triangle has length 4. How long is each leg?
Answers
Answer:
you know 2 sides are the same on an a silly triangle.. I mean isosceles.. so the hypotenuse will be longer but the other two sides are the same
use \(C^{2}\) = \(A^{2}\) + \(B^{2}\) ( Pythagoras theorem )
Step-by-step explanation:
\(4^{2}\) = \(A^{2}\) +\(A^{2}\) ( b/c the side are the same length the can both be called A )
16 = 2\(A^{2}\)
8 = \(A^{2}\)
\(\sqrt{8}\) = A
not a whole number but.. it's still a good answer square root of 8 is about 2.8284 on my calculator
. Lucy orders books from an online bookstore. She pays $12 per book and $8.95 for shipping and handling. How much does she pay in all for 13 books?
Answers
Answer:
If the shipping is for all books then the total cost is 164.95
y=2x+3=
please help me i have test
Answers
\( \: \: \: \: \: \)
\( = \: \: \: x = - \frac{3}{2 } \\ \\ \)
hope it helpsrefer to attachment
\( \: \: \: \: \: \)
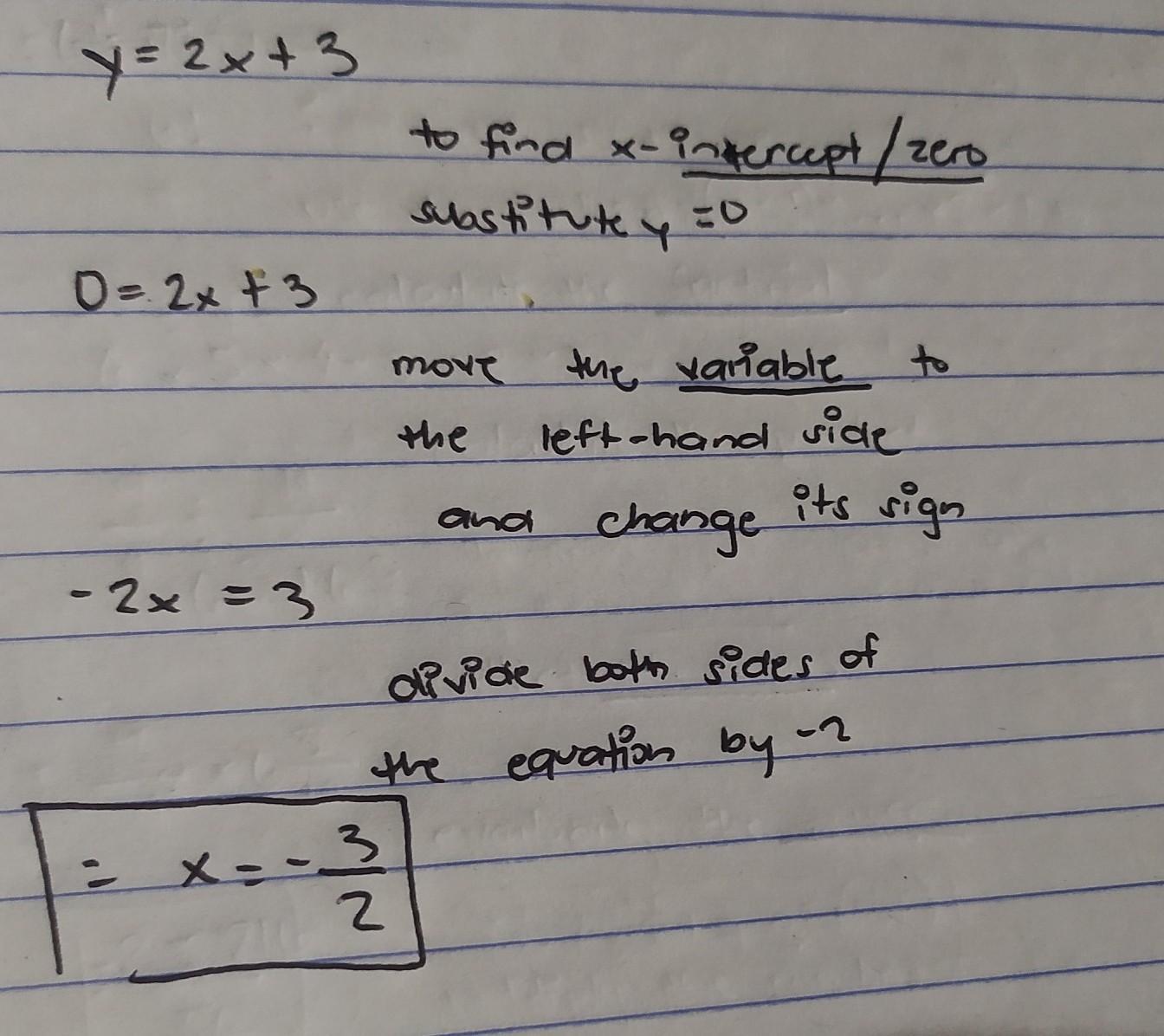
4. Round the number 5,997 to the nearest hundred.

Answers
Answer:
6,000
Step-by-step explanation:
Solve for x. Please highlight your final answer.
I NEED HELP ASAP ITS DUE TODAY

Answers
Answer:
1. square root 187.61 OR 13.7
2. square root 115 OR 10.7
Step-by-step explanation:
I believe these are right, if they are not tell me
Prove the identity.
tan^5x = tan x (sec² x - 2 sec² x + 1)

Answers
goal:tan^5x=tanx(sec²x-2sec²x+1)
proof: from l.h.s to r.h.s
tan^5x=(tanx)^5=((tanx)(tan²x)(tan²x))
from trigonometry identity
(tan²x)=sec²x-1
tan^5x=(tanx(sec²x-1)(sec²x-1))
=(tanx(sec^4x-sec²x-sec²x+1))
=(tanx(sec^4x-2sec²x+1))
proved
what is the wavelength (in nm) of an electron moving with a speed of 5.97 mms-1, the mass of an electron is 9.11 x 10-28 g.
Answers
the wavelength of the electron is approximately 122 nm To find the wavelength of an electron, we can use the de Broglie wavelength formula:
wavelength (λ) = h / (m * v)
where:
- h is Planck's constant (6.63 x 10^-34 Js)
- m is the mass of the electron (9.11 x 10^-28 g, which needs to be converted to kg)
- v is the speed of the electron (5.97 mm/s, which needs to be converted to m/s)
Step 1: Convert the mass of the electron to kg:
9.11 x 10^-28 g * (1 kg / 1000 g) = 9.11 x 10^-31 kg
Step 2: Convert the speed of the electron to m/s:
5.97 mm/s * (1 m / 1000 mm) = 5.97 x 10^-3 m/s
Step 3: Plug the values into the de Broglie wavelength formula:
λ = (6.63 x 10^-34 Js) / (9.11 x 10^-31 kg * 5.97 x 10^-3 m/s)
Step 4: Calculate the wavelength:
λ = (6.63 x 10^-34 Js) / (5.44 x 10^-33 kg m/s) ≈ 1.22 x 10^-10 m
Step 5: Convert the wavelength to nm:
1.22 x 10^-10 m * (1 x 10^9 nm / 1 m) ≈ 122 nm
So, the wavelength is approximately 122 nm.
to learn more about wavelength click here :
brainly.com/question/24452579
#SPJ11
The amount of interest earned every year with simple interest is constant.
true or false
Answers
Answer:
True.
Step-by-step explanation:
If I = prt, They are all being multiplied together, therefor being constant.
Which equation can you solve to find the potential solutions to the equation log2x log2(x – 6) = 4? x2 – 6x – 4 = 0 x2 – 6x – 8 = 0 x2 – 6x – 16 = 0.
Answers
To solve the question we must know about Logarithm.
LogarithmA log function is a way to find how much a number must be raised in order to get the desired number.
\(a^c =b\)
can be written as
\(\rm{log_ab=c\)
where a is the base to which the power is to be raised,
b is the desired number that we want when power is to be raised,
c is the power that must be raised to a to get b.
For example, let's assume we need to raise the power for 10 to make it 1000 in this case log will help us to know that the power must be raised by 3.
\(\rm{log_{10}1000=3\)
The value of input can not be negative, the value of x is 8.
Given to us\(\rm{ log_2x+log_2(x-6)= 4\)Solution\(\rm{ log_2x+log_2(x-6)= 4\)
Using \(log_ab + log_ac = log_a(bc)\),\(\rm{ log_2x(x-6)= 4\)
Taking antilog,\( x(x-6)= 2^4\)
Doing factorization\(x^2 -6x -16=0\\ x^2 -8x +2x-16=0\\ x(x-8)+2(x-8)=0\\ (x+2)(x-8) = 0\)
Equating factors against 0,
1. \((x+2)=0\\ x=-2\)
2. \((x-8)=0\\ x=8\)
As the value of input can not be negative, the value of x is 8.
Hence, the value of x is 8.
Learn more about Logarithm:
https://brainly.com/question/3072484
Answer:
The answer is C
Step-by-step explanation:
C) x2 – 6x – 16 = 0
What is the volume of the cylinder below?
Use 3.14 for pi.

Answers
Answer:
about =502.65
Step-by-step explanation:
a) What is the size of angle f?
Give the angle fact that you used for your answer.
b) Which angle fact shows that angle f and angle g are equal?

Answers
Answer:
a. The size of angle x is 126
b. alternate angles are equal
Step-by-step explanation:
a. Angles on a straight line add up to 180
This implies 54+x=180
×=180-54
x=126
The length of the longer leg of a right triangle i 6inche more than twice the length of the horter leg. The length of the hypotenue i 9inche more than twice the length of the horter leg. Find the ide length of the triangle
Answers
The length of shorter leg is 15 inches, length of longer leg is 36 inches and the length of hypotenuse is 39 inches.
What is right triangle?
A right triangle, also known as a right-angled triangle, an orthogonal triangle, or formerly a rectangled triangle, is a triangle with one right angle, meaning that its two sides are perpendicular. Trigonometry's foundation is the relationship between the right triangle's sides and other angle.
Let,
x = Longer leg of triangle
y = Shorter leg of triangle
h = Hypotenuse of triangle
Given: The length of the longer leg of a right triangle is 6inches more than twice the length of the shorter leg.
The length of the hypotenuse is 9inches more than twice the length of the shorter leg.
⇒ x = 6 + 2y
h = 9 + 2y
The given triangle is a right angled triangle.
⇒ x^2 + y^2 = h^2
(6 + 2y)^2 + y^2 = (9 + 2y)^2
36 + 24y + 4y^2 + y^2 = 81 + 36y + 4y^2
36 + 24y + 5y^2 = 81 + 36y + 4y^2
36 - 81 + 24y - 36y + 5y^2 - 4y^2 = 0
-45 - 12y + y^2 = 0
y^2 - 12y - 45 = 0
y^2 - 15y + 3y - 45 = 0
y(y - 15) + 3(y - 15) = 0
(y - 15)(y + 3) = 0
y - 15 = 0, y + 3 = 0
y = 15, y = -3
Since the length is not negative.
So, y = 15
Hence,
Shorter leg = 15 inchs
Longer leg = 6 + 2y = 6 + 2(15) = 36 inches
Hypotenuse = 9 + 2y = 9 + 2(15) = 39 inches
To know more about right triangle, click on the link
https://brainly.com/question/29801705
#SPJ4
if a confusion matrix shows 46 tp, 6 fn, 500 tn, and 4 fp, what is the precision ratio? (round your answer to 2 decimal places.)
Answers
Answer:
Step-by-step explanation:
Precision is defined as the ratio of true positives (TP) to the total predicted positives (TP + FP). In this case, the confusion matrix shows 46 TP and 4 FP, so the precision can be calculated as:
precision = TP / (TP + FP) = 46 / (46 + 4) = 0.92
Rounding to 2 decimal places, the precision ratio is 0.92.
HELP ME PLEASE!!! it’s for algebra and i really need to get this awnser right!! please literally anyone help me

Answers
Answer:
Below
Step-by-step explanation:
Start with point (3,5) slope (5/3) form:
(y-5) = 5/3 (x-3) expand
y-5 = 5/3 x -5 re-arrange by adding 5 to both sides
y = 5/3 x done!
Please help me
-5 x (-5)
Answers
Answer:
25x
Step-by-step explanation:
\(-5x\left(-5\right)\)
Frist Multiply the numbers: 5(-5) = -25
\(=-\left(-25\right)x\)
remove the parentheses.
=25x
Answer: 25x
Step-by-step explanation:
According to a recent survey of 1,001 adult Canadians, of respondents do not want to be unionized 27 percent 54 percent 19 percent 35 percent (E) 77 percent
Answers
According to a recent survey of 1,001 adult Canadians, 27 percent of respondents indicated that they do not want to be unionized.
The survey of 1,001 adult Canadians asked respondents about their preference regarding unionization. Out of the total respondents, 27 percent expressed that they do not want to be unionized. This percentage represents the proportion of individuals who indicated a lack of interest or desire to be part of a labor union.
It is important to note that without additional information about the survey methodology, sample representation, and any potential biases, the result should be interpreted within the context of the survey's limitations. The percentage obtained from the survey reflects the preferences of the respondents in the sample but may not necessarily represent the opinions of the entire population of adult Canadians.
Learn more about proportion here:
https://brainly.com/question/31548894
#SPJ11
I WILL GIVE BRAINLIST enter the correct answer in the box. Write your answer in the form y=mx+b using the appropriate inequality symbol in place of the equal sign

Answers
Answer:
y > 4x + 1
Step-by-step explanation:
Look at the graph. The y-intercept is 1, so we have
y = mx + 1
Now let's find the slope.
Go from the intercept 4 units up and 1 unit to the right. You are at point (1, 5) which is a point on the graph.
slope = m = rise/run = 4/1 = 4
The equation of the dashed line is
y = 4x + 1
The shaded area is "above" the line, so the inequality is
y > 4x + 1
Answer:
y > 4x + 1
Step-by-step explanation:
Hope this is right.
1. If n=590 and ˆpp^ (p-hat) =0.27, find the margin of error at a 90% confidence level
Give your answer to three decimals
2. In a recent poll, 550 people were asked if they liked dogs, and 10% said they did. Find the margin of error of this poll, at the 99% confidence level.
Give your answer to three decimals
3. If n = 500 and ˆpp^ (p-hat) = 0.85, construct a 95% confidence interval.
Give your answers to three decimals
< p <
4. A political candidate has asked you to conduct a poll to determine what percentage of people support her.
If the candidate only wants a 4% margin of error at a 90% confidence level, what size of sample is needed?
Give your answer in whole people.
5. Out of 100 people sampled, 7 preferred Candidate A. Based on this, estimate what proportion of the voting population (ππ) prefers Candidate A.
Use a 90% confidence level, and give your answers as decimals, to three places.
< ππ <
6. You work for a marketing firm that has a large client in the automobile industry. You have been asked to estimate the proportion of households in Chicago that have two or more vehicles. You have been assigned to gather a random sample that could be used to estimate this proportion to within a 0.04 margin of error at a 99% level of confidence.
a) With no prior research, what sample size should you gather in order to obtain a 0.04 margin of error? Round your answer up to the nearest whole number.
n = households
b) Your firm has decided that your plan is too expensive, and they wish to reduce the sample size required. You conduct a small preliminary sample, and you obtain a sample proportion of ˆp=0.2p^=0.2 . Using this new information. what sample size should you gather in order to obtain a 0.04 margin of error? Round your answer up to the nearest whole number.
n = households
7. In a sample of 240 adults, 161 had children. Construct a 95% confidence interval for the true population proportion of adults with children.
Give your answers as decimals, to three places
< p <
8. The confidence interval for a population porportion is (0.48, 0.68). What the the sample proportion and the margin of error. I
ˆp=p^=
Margin of Error =
Answers
1. The margin of error can be determined by using the following formula: Margin of error = z*√(p^(1-p^)/n)Where z is the z-score for the confidence level, p^ is the sample proportion, and n is the sample size.
For a 90% confidence level, the z-score is 1.645. Therefore, the margin of error is:Margin of error = 1.645 * √((0.27*(1-0.27))/590)≈ 0.0472 or 0.047 (rounded to three decimal places)
2. To find the margin of error at a 99% confidence level, we can use the formula:Margin of error = z*√(p^(1-p^)/n)For a 99% confidence level, the z-score is 2.576.
Therefore, the margin of error is:Margin of error = 2.576 * √((0.1*(1-0.1))/550)≈ 0.0464 or 0.046 (rounded to three decimal places)
3. The formula for a confidence interval for a proportion is:p^ ± z*(√(p^(1-p^)/n))where z is the z-score for the desired confidence level.For a 95% confidence level, the z-score is 1.96. Therefore, the confidence interval is:0.85 ± 1.96*(√(0.85*(1-0.85)/500))≈ 0.819 to 0.881 (rounded to three decimal places)
4. The formula for sample size required to achieve a desired margin of error is:n = (z^2 * p^*(1-p^))/E^2where z is the z-score for the desired confidence level, p^ is the estimated proportion, and E is the desired margin of error. Rearranging this formula to solve for n, we get:n = (z^2 * p^*(1-p^))/E^2For a 90% confidence level and a desired margin of error of 4%, the z-score is 1.645 and the estimated proportion is 0.5 (assuming no prior information is available).
Therefore, the sample size required is:n = (1.645^2 * 0.5*(1-0.5))/(0.04^2)≈ 426.122. Rounded up to the nearest whole number, the sample size required is 427.5. To obtain a margin of error of 4% with a 99% confidence level, the z-score is 2.576. The estimated proportion is 0.5 (assuming no prior information is available).
Therefore, the sample size required is:n = (2.576^2 * 0.5*(1-0.5))/(0.04^2)≈ 676.36. Rounded up to the nearest whole number, the sample size required is 677.7. To obtain a margin of error of 4% with a 99% confidence level, given that the sample proportion is 0.2, we can use the following formula to calculate the required sample size:n = (z^2 * p^*(1-p^))/E^2where z is the z-score for the desired confidence level, p^ is the sample proportion, and E is the desired margin of error.
Rearranging this formula to solve for n, we get:n = (z^2 * p^*(1-p^))/E^2For a 99% confidence level, a margin of error of 4%, and a sample proportion of 0.2, the z-score is 2.576. Therefore, the sample size required is:n = (2.576^2 * 0.2*(1-0.2))/(0.04^2)≈ 1067.78. Rounded up to the nearest whole number, the sample size required is 1068.7. The formula for a confidence interval for a proportion is:p^ ± z*(√(p^(1-p^)/n))where z is the z-score for the desired confidence level.For a 95% confidence level, the z-score is 1.96.
Therefore, the confidence interval is:161/240 ± 1.96*(√((161/240)*(1-161/240)/240))≈ 0.627 to 0.760 (rounded to three decimal places)8. The sample proportion is the midpoint of the confidence interval, which is: (0.48 + 0.68)/2 = 0.58The margin of error is half the width of the confidence interval, which is: (0.68 - 0.48)/2 = 0.1
For more such questions on confidence level
https://brainly.com/question/30540650
#SPJ8
Iran's puppy weighed 3/4 pounds. His kitten weighed 1/5 pounds. What was the total weight of Ira's two pets?
Answers
Answer:
19/20 punds
Step-by-step explanation:
I graduatiated 4th grade
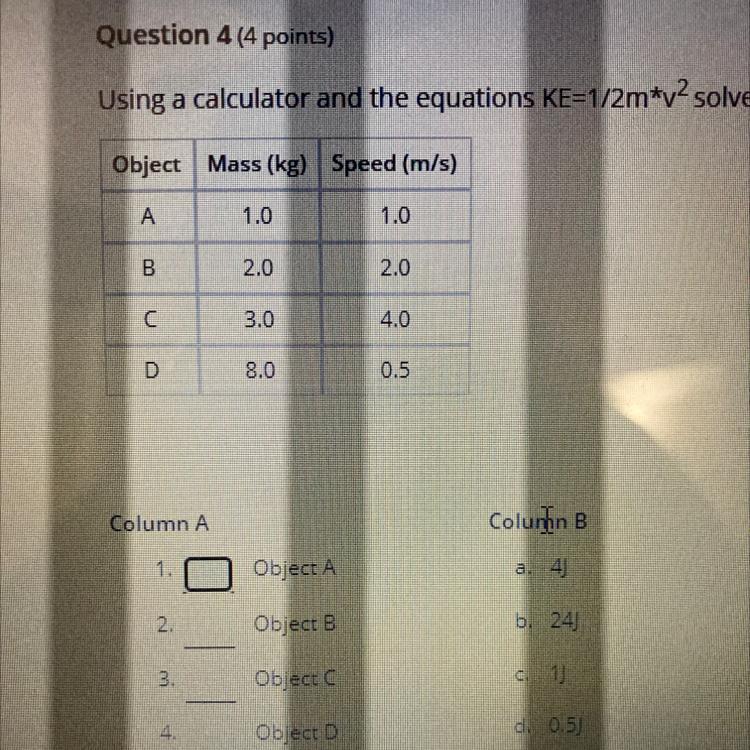
Hi I really need help thx.
Answers
Answer:
A. KE=1/2; B. KE=4; C. KE=24; D. KE=1
Step-by-step explanation:
A. KE=1/2*1*1²=1/2
B. KE=1/2*2*2²=1*4=4
C. KE=1/2*3*4²=1.5*16=24
D. KE=1/2*8*0.5²=4*0.25=1
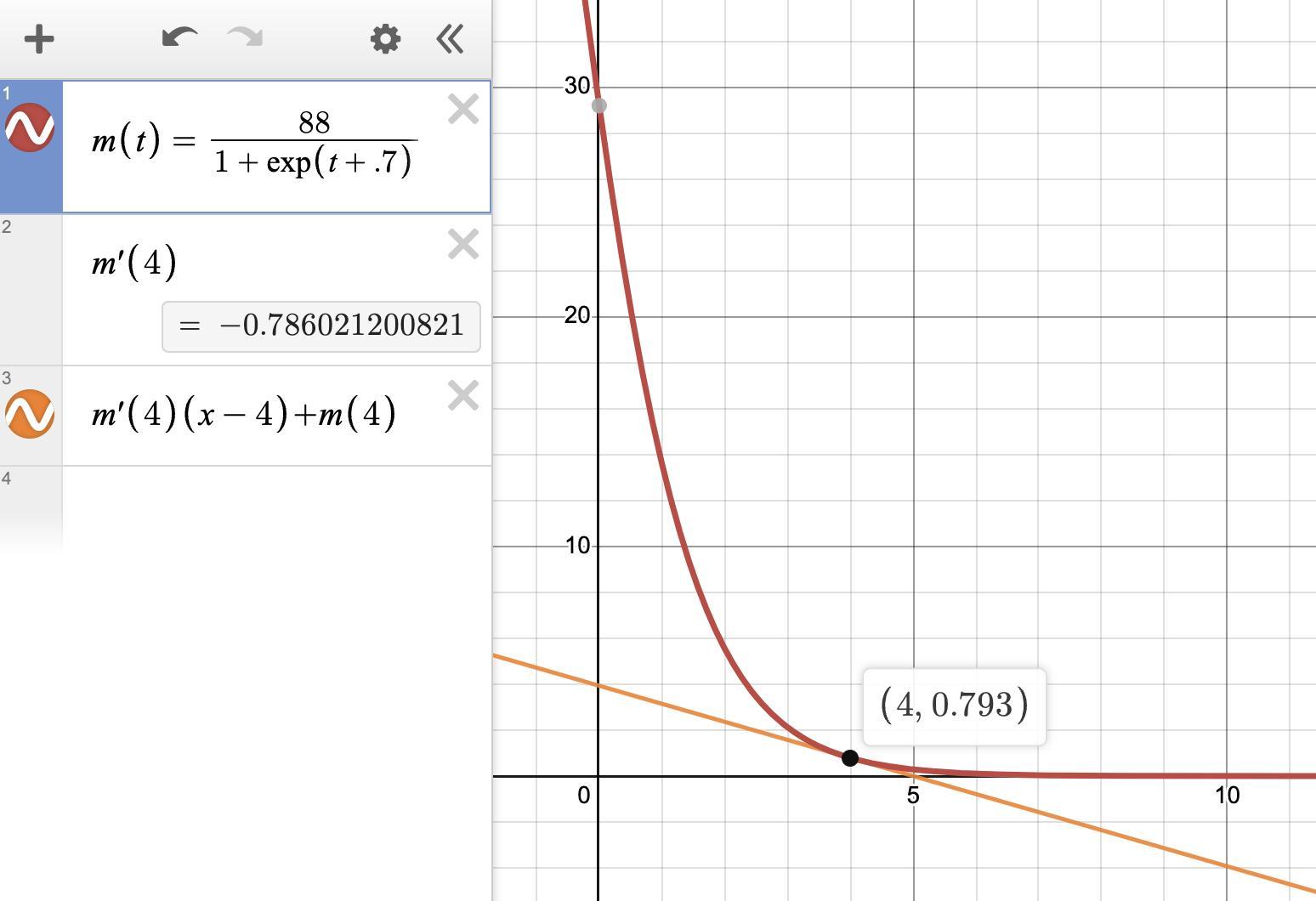
the amount of medication, in milligrams, in a patient's bloodstream after t hours, can be represented by the following function: m of t equals 88 over the quantity 1 plus e to the x plus 7 tenths power end quantity what is the rate of change for the amount of medication in the patient's bloodstream after 4 hours?
Answers
Answer:
about -0.79 mg/hour
Step-by-step explanation:
You want the rate of change of the amount of medication in a patient after 4 hours if the amount after t hours is modeled by y=88/(1+e^(t+0.7)).
Rate of changeThe rate of change is found by taking the derivative of the function with respect to time. Let u = 1+e^(t+0.7). Then du/dt = e^(t +0.7).
The function can be written ...
y = 88/u = 88·u^-1
so its derivative is ...
dy/dt = (-88·u^-2)·du/dt
dy/dt = -88(e^(t +0.7))/(1 +e^(t +0.7))^2
At t=4The value of the rate of change at t=4 is ...
dy/dt = -88(e^(4 +0.7))/(1 +e^(4 +0.7))^2 ≈ -88(109.95)/(1 +109.95)^2
dy/dt ≈ -0.78602 ≈ -0.79 . . . . . . mg/h
The rate of change in the amount of medication is about -0.79 mg/h.

The following relationship is know to be true for two angles A and B : sin(A)cos(B)+cos(A)sin(B)=0.985526 Express A in terms of the angle B. Work in degrees and report numeric values accurate to 2 decimal places. A= Enter your answer as an expression. Be sure your variables match those in the question. If sinα=0.842 and sinβ=0.586 with both angles' terminal rays in Quadrant-I, find the values of (a) cos(α+β)= (b) sin(β−α)= Your answers should be accurate to 4 decimal places.
Answers
sin(β−α) = -0.9345 is accurate to four decimal places.
Let's find the solution to the given problem.The given relationship is sin(A)cos(B) + cos(A)sin(B) = 0.985526. The relationship sin(A)cos(B) + cos(A)sin(B) = sin(A+B) is also known as the sum-to-product identity. We can therefore say that sin(A+B) = 0.985526.
Let sinα = 0.842 and sinβ = 0.586. This places both angles' terminal rays in the first quadrant. We can therefore find the values of cosα and cosβ by using the Pythagorean Identity which is cos²θ + sin²θ = 1. Here, cos²α = 1 - sin²α = 1 - (0.842)² = 0.433536 which gives cosα = ±0.659722.
Here, cos²β = 1 - sin²β = 1 - (0.586)² = 0.655956 which gives cosβ = ±0.809017. From the problem, we need to find the values of cos(α+β) and sin(β−α).
a) Using the sum identity, cos(α+β) = cosαcosβ - sinαsinβ, which is cosαcosβ - sinαsinβ = (0.659722)(0.809017) - (0.842)(0.586) = 0.075584.Therefore, cos(α+β) = 0.0756. This is accurate to four decimal places.b) Using the difference identity, sin(β−α) = sinβcosα - cosβsinα, which is sinβcosα - cosβsinα = (0.586)(0.659722) - (0.809017)(0.842) = -0.93445Therefore, sin(β−α) = -0.9345. This is accurate to four decimal places.
To know more about decimal refer here:
https://brainly.com/question/30958821
#SPJ11
hey! i’ll give brainliest please help

Answers
Answer:
conjunction
Step-by-step explanation:
Answer:
Conjunction is correct answer. (I think)
You are working with a satellite image of Anchorage, AK (∼150
∘
W) with the time stamp 0300Z, Dec. 3 2011. This means that it was 3AM on Dec. 3 at the Prime Meridian when the image was taken. What was the local time and day in Anchorage when the image was taken?
Answers
the local time in Anchorage when the image was taken was 5:00 PM, and the local day was Dec. 2, 2011.
To determine the local time and day in Anchorage when the satellite image was taken, we need to consider the time difference between the Prime Meridian (0 degrees longitude) and Anchorage, Alaska (approximately 150 degrees west longitude).
Each time zone is approximately 15 degrees wide, representing a one-hour difference in local time. Anchorage is in the Alaska Standard Time (AKST) zone, which is typically UTC-9 (nine hours behind UTC) during standard time.
Given that Anchorage is about 150 degrees west of the Prime Meridian, we can calculate the time difference as follows:
150 degrees / 15 degrees per hour = 10 hours
Therefore, when the image was taken at 0300Z (3:00 AM), Dec. 3, 2011, at the Prime Meridian, the local time and day in Anchorage were:
3:00 AM - 10 hours = 5:00 PM, Dec. 2, 2011
So, the local time in Anchorage when the image was taken was 5:00 PM, and the local day was Dec. 2, 2011.
learn more about degrees here:
https://brainly.com/question/364572
#SPJ11
According to the rational root theorem, the following are potential roots of f(x) = 6x4 + 5x3 – 33x2 – 12x + 20. negative five-halves, –2, 1, ten-thirds which is an actual root of f(x)?
Answers
As per the rational root theorem, the actual root of the polynomial is - 5/2
The term polynomial refers the algebraic expression in which the exponents of all variables should be a whole number
Here we have given that f(x) = 6x⁴ + 5x³ – 33x² – 12x + 20. and we need to find which is an actual root of f(x).
In order to find the root for the polynomial we have to apply each value as the replacement of x in the polynomial.
And then we have to find in which one makes the polynomial result as zero.
First we have to take the value of x as -5/2, then the polynomial equation be like,
Here we have to substitute x=-5/2, then we get
=> f(-5/2) = 6(-5/2)⁴ + 5(-5/2)³ - 33(-5/2)² - 12(-5/2) + 20
=> f(-5/2) = 6(625/16)-5(125/8)-33(25/4)+30+20
when we simplify this one then we get,
=> f(-5/2)=(1,875-625-1,650+400)/8
=> f(-5/2)=0/8
Here we know that if we zero by any number we get the result as zero.
Therefore, f(-5/2)=0 then x=-5/2 is a root of f(x)
To know more about Polynomial here.
https://brainly.com/question/11536910
#SPJ4
Answer:
its A
Step-by-step explanation:
Just took the test