HELP ILL GIVE YOU 50 POINTS IF SOMEONE HELPS ME What is the total area of the figure below?
28 ft
4 ft 6 ft
14 ft
2 11
A. 47 ft2
B. 52 ft2
C. 168 ft2
D. 402 ft2

Answers
Answer:
D: 402 ft squared
Step-by-step explanation:
Trapezoid: 4 + 6 over 2 multiplied by 2 equals 10
28 x 14 = 392
392 + 10 = 402
hopes this helps plz mark me brainliest
Related Questions
Question in picture solve

Answers
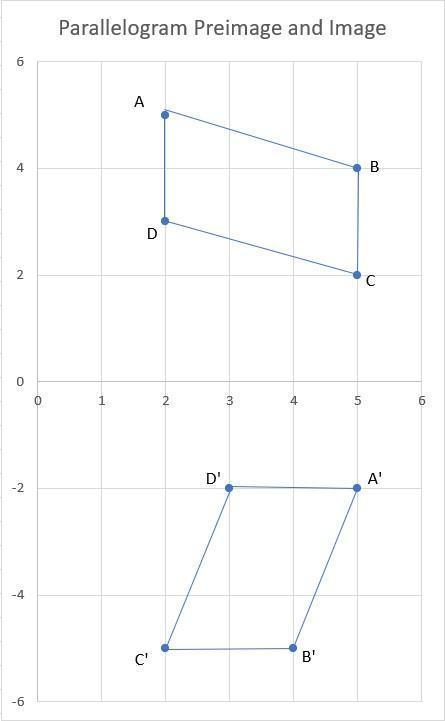
Parallelogram ABCD is rotated to create image A'B'C'D'.
Answers
The transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
The rule that describes the transformation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
To understand this, let's apply the transformation rule to each vertex of the original parallelogram ABCD:
Point A (2, 5) becomes A' (-5, 2).
Point B (5, 4) becomes B' (-4, 5).
Point C (5, 2) becomes C' (-2, 5).
Point D (2, 3) becomes D' (-3, 2).
By applying the transformation rule, we observe that the x-coordinate of each point becomes the negative of the original y-coordinate, and the y-coordinate becomes the original x-coordinate.
This transformation is a 90-degree counterclockwise rotation about the origin (0, 0) on the coordinate plane. The image parallelogram A'B'C'D' is obtained by rotating the original parallelogram ABCD by 90 degrees counterclockwise.
Visually, this transformation can be seen as the original parallelogram being rotated around the origin, where the x-axis becomes the y-axis, and the y-axis becomes the negative x-axis.
Therefore, the transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
For more such questions on parallelogram visit:
https://brainly.com/question/970600
#SPJ8
Find (a) f(g(x)), (b) g(f(x)), and (c) f(f(x)).
f(x) = 2x², g(x) = x-1
a. f(g(x)) =
b. g(f(x)) =
c. f(f(x)) = .
State the domain and range of each composition.
Answers
Required value of f(g(x)), g(f(x)), f(f(x)) are 2x²- 4x + 2 , 2x² -1 and 8x⁴ respectively.
the range of f(g(x)) is [0, ∞), the range of g(f(x)) = = 2x²-1 is [-1,∞) and the range of f(f(x)) is [0, ∞).
What is composition of functions?
Suppose we are given two functions f(x), g(x). We construct a new function h(x) as follows. plug 'x' into g(x) and find its value. then plugin this value into f(x), that is find f(g(x)). Now set h(x) = f(g(x)). This new function h(x) is called the composition of functions f(x) and g(x).
a. f(g(x)) = 2 * (x - 1)² = 2(x² - 2x + 1) = 2x²- 4x + 2 Since fg(x)) is a polynomial its domain is all real numbers. to find the range note that f(g(x)) = 2 * (x - 1) ² . and the range of the square is all non-negative real numbers. So the range of f(g(x)) is [0, ∞).
b. g(f(x)) = (2x²) - 1 =2x² -1.g(f(x)) is a polynomial function, so the domain of g(f(x)) is (-∞, ∞). Note that the range of 2x² is [0, ∞). So the range of g(f(x)) = 2x²-1 is [-1,∞)
c. f(f(x)) = 2 * (2x²)² = 2(4x⁴) = 8x⁴ . Since this is a polynomial function, the domain is (-∞, ∞), and clearly the range is [0, ∞).
To know more about composition of functions, visit:
https://brainly.com/question/5614233
#SPJ1
you have been given the following data: x 1 3 4 6 9 8 10 y 1 8 15 33 75 70 95 test to determine whether there is evidence of a linear relationship. please write the test hypothesis:
Answers
To test whether there is evidence of a linear relationship between the given data (x and y values), we can perform a hypothesis test.
Step 1: State the null hypothesis (H0) and the alternative hypothesis (H1).
H0: There is no linear relationship between x and y (i.e., the correlation coefficient, r, is equal to 0)
H1: There is a linear relationship between x and y (i.e., the correlation coefficient, r, is not equal to 0)
Step 2: Calculate the correlation coefficient, r, using the given data. You can do this using a statistical calculator or software.
Step 3: Determine the critical value for the correlation coefficient at a chosen significance level (e.g., 0.05).
Step 4: Compare the calculated correlation coefficient, r, to the critical value. If |r| is greater than the critical value, reject the null hypothesis (H0) in favor of the alternative hypothesis (H1), indicating evidence of a linear relationship. If |r| is less than or equal to the critical value, fail to reject the null hypothesis (H0), suggesting there is not enough evidence to support a linear relationship.
By following these steps, you can test the hypothesis and determine if there is evidence of a linear relationship between the given data points.
Learn more about test hypothesis here, https://brainly.com/question/15980493
#SPJ11
Drag the term to the corresponding probability. Each term may be used only once. CertainLikelyUnlikelyImpossible Probability Term Probability < 12 Probability = 0 Probability = 1 Probability > 12
Answers
Thus, the probability are Zero represents the impossibility.
1/2 equals probable and unlikely
1 = event happens.
Because we don't know how something will turn out, we might talk about the probability of one outcome or the potential for several outcomes.
Typically, the likelihood is stated as the proportion of favourable events to all other potential outcomes in the sample space.
The probability of an event is calculated using the formula P(E) = (Number of favourable outcomes) (Sample space).
Given that probability can only be a number between 0 and 1,
The zeroth value is the impossible.
so there is a 50% chance for both likely and unlikely.
If 1, the event must take place.
To know more about the probability , click the below link
brainly.com/question/795909
#SPJ4
Please answer correctly !!!!!!!!!!!!!!! Will mark brainliest !!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
I believe it is 14.
Step-by-step explanation:
Answer: The value of x is 14°
Step-by-step explanation:
Since line m is parallel to n, then then the two given angles will have the same measures. Meaning that 136 degrees has to equation (9x+10).
Set them to equal each other and solve for x.
9x + 10 = 136
- 10 -10
9x = 126
x= 14
(Chapter 12) If u * v = 0 and u X v = 0, then u or v = 0
Answers
Therefore, in either partial derivatives, we have u = 0 or v = 0.
The given information implies that two vectors u and v satisfy:
u * v = 0, where * denotes the dot product between vectors.
u X v = 0, where X denotes the cross product between vectors.
From the first equation, we know that the angle between u and v is either 90 degrees or 270 degrees. That is, u and v are orthogonal (perpendicular) to each other.
From the second equation, we know that the magnitude of the cross product u X v is equal to the product of the magnitudes of u and v multiplied by the sine of the angle between them. Since u and v are orthogonal, the angle between them is either 90 degrees or 270 degrees, which means that the sine of the angle is either 1 or -1. Therefore, we have:
|u X v| = |u| * |v| * sin(θ)
= 0
Since the magnitudes of u and v are non-negative, it follows that sin(θ) must be zero. This can only happen if the angle between u and v is either 0 degrees (i.e., u and v are parallel) or 180 degrees (i.e., u and v are anti-parallel).
In the case where u and v are parallel, we have:
u * v = |u| * |v| * cos(θ)
= |u|²
= 0
This implies that |u| = 0, which means that u = 0.
In the case where u and v are anti-parallel, we have:
u * v = |u| * |v| * cos(θ)
= -|u|²
= 0
This again implies that |u| = 0, which means that u = 0.
To know more about partial derivatives,
https://brainly.com/question/21661447
#SPJ11
How much is 159 pounds in Kg?
Answers
The value 159 pounds is equal to 72.12 kilograms. The kilogram (kg) is a unit of mass, used for measuring weight.
It's worth noting that the kilogram is defined as the mass of a particular cylinder of platinum-iridium alloy kept at the International Bureau of Weights and Measures, while the pound is based on the historical use of a pound of wrought iron as a unit of mass. In everyday usage, however, the kilogram is often preferred for its use in scientific research and international trade.
This can be calculated by dividing 159 by 2.20462.
= 159/ 2.20462
= 72.12 kg
So, 159 pounds is equal to 72.12 kilograms.
To know more about pounds click here:
https://brainly.com/question/29181271#
#SPJ11
easy prob pls help i need

Answers
The dimensions of the rectangular poster are 9 inches by 22 inches.
Let's assume the width of the rectangular poster is x inches.
According to the given information, the length of the poster is 4 more inches than two times its width. So, the length can be expressed as 2x + 4 inches.
The formula for the area of a rectangle is length × width. In this case, the area is given as 198 square inches.
Therefore, we have the equation:
(2x + 4) × x = 198
Expanding the equation:
\(2x^2 + 4x = 198\)
Rearranging the equation to standard quadratic form:
\(2x^2 + 4x - 198 = 0\)
To solve this quadratic equation, we can use factoring, completing the square, or the quadratic formula. Let's use the quadratic formula:
x = (-b ± √\((b^2 - 4ac\))) / (2a)
Plugging in the values:
x = (-4 ± √\((4^2 - 4(2)(-198)))\) / (2(2))
x = (-4 ± √(16 + 1584)) / 4
x = (-4 ± √1600) / 4
x = (-4 ± 40) / 4
Simplifying:
x = (-4 + 40) / 4 = 9
x = (-4 - 40) / 4 = -11
Since we are dealing with dimensions, the width cannot be negative. Therefore, the width of the poster is 9 inches.
Substituting the value of x back into the length equation:
Length = 2x + 4 = 2(9) + 4 = 18 + 4 = 22 inches
For more such questions on rectangular visit:
https://brainly.com/question/2607596
#SPJ8
samantha wants too pour 3 gallons of water into cups. How many cups will be used? Picture your solution or write I'll make it the brainliest!
Answers
Answer:
48
Step-by-step explanation:
there are 16 cups in a gallon therefore you would multiply 16 times the number of gallons she uses which is 3 so 16 times 3 or you could do 16+16+16 which both would get you 48 so she would need 48 cups to make 3 gallons. hope this helps have a good rest of your night :)❤
On a coordinate plane, a graph shows Street on the x-axis and Avenue on the y-axis. A line is drawn from Tia to Lei. Tia is at (4, 8) and Lei is at (12, 20). Tia lives at the corner of 4th Street and 8th Avenue. Lei lives at the corner of 12th Street and 20th Avenue. The fruit market is Three-fourths the distance from Tia’s home to Lei's home.
Answers
Answer:
(10, 17)
Step-by-step explanation:
It might be easier to explain with a picture or drawing, but I am new to this, so I would try using words.
Assuming the fruit market is on that straight line from Tia's home to Lei's, So we look at both address (coordinates)
From Tia to Lei, x coordinate is from 4 to 12, that's increased by 8, divide by 4, one step is 2.
y coordinate is from 8 to 20, an increase of 12, divide by 4 again, one step is 3.
The fruit market is at 3/4 distance, so 3 steps, on both x and y coordinates.
x: 4+6 = 10
y: 8+9=17
The fruit market is at point (10,17)
What is graph?
A graph can be defined as a pictorial representation or a diagram that represents data or values.
The point (x,y) which divides the segment AB with endpoints at A(x₁,y₁) and B(x₂,y₂) in ratio m:n has cordinates
\(x= \dfrac{nx_1+nx_2}{m+n}\)
\(y= \dfrac{ny_1+ny_2}{m+n}\)
Tia is at P(4, 8) and Lei is at Q(12, 20).
The fruit market (F) is three-fourths the distance from Tia’s home to Lei's home, then PM : PQ = 3:4 or PM : MQ = 3:1
So,
\(x= \dfrac{1.4+3.12}{3+1} = \dfrac{4+36}{4} = \dfrac{40}{4} = 10 \\y= \dfrac{1.8+3.20}{3+1} = \dfrac{8+60}{4} = \dfrac{68}{4} = 17\)
Hence, the fruit market is at point (10,17) which means it is placed at the corner of 10th Street and 17th Avenue.
Learn more about graph here:
brainly.com/question/16608196
#SPJ5
Jane and Jim collect coins. Jim has five more than twice the amount Jane has. They have 41 coins altogether. How many coins does Jim have? How many coins does Jane have?
Answers
Jane has 12 coins and Jim has 29 coins.
What is the equation?We know that this is a word problem and the first thing that we have to do is to form the equation from the problem that have been given to us here. This is what we shall now proceed to do below.
Let the number of coins that Jane has be x
Number of coins that Jim has = 5 + 2x
Total number of coins = 41
Thus we have that;
x + 5 + 2x = 41
3x + 5 = 41
3x = 41 - 5
3x = 36
x = 12
This implies that Jane has 12 coins and Jim has 5 + 2(12) = 29 coins
Learn more about equation:https://brainly.com/question/29657983
#SPJ4
Using the vertical angle image from problem 1, let ∠2 = 4x-4 and ∠4 = x+50.
A. What is the value of x?
B. What is the measure of ∠2?
C. Find the measure of ∠3.

Answers
Answer:
A) x = 18, B) ∠2 = 68°, C) ∠3 = 112°Step-by-step explanation:
According to vertical angles theorem, when two lines intersect the opposite angles are equal and adjacent angles are supplementary.
Given∠2 = 4x-4 and ∠4 = x+50A) Find the value of x:
4x - 4 = x + 504x - x = 50 + 43x = 54x = 54/3x = 18B) Find the measure of angle 2:
∠2 = 4*18 - 4 = 72 - 4 = 68C) Angles 2 and 3 are supplementary so their sum is 180°.
∠2 + ∠3 = 18068 + ∠3 = 180∠3 = 180 - 68∠3 = 112°Answer:
A. x = 18
B. m∠2 = 68°
C. m∠2 = 112°
Step-by-step explanation:
Given:
\(\angle 2=4x-4\)\(\angle4=x+50\)Part AVertical Angles Theorem
When two straight lines intersect, the opposite vertical angles are congruent.
Therefore:
\(\implies \angle 2 = \angle 4\)
\(\implies 4x-4= x+50\)
\(\implies 4x-4-x= x+50-x\)
\(\implies 3x-4= 50\)
\(\implies 3x-4+4= 50+4\)
\(\implies 3x=54\)
\(\implies 3x\div 3=54 \div 3\)
\(\implies x=18\)
Part BTo find the measure of ∠2, substitute the found value of x into the given expression for ∠2:
\(\implies m\angle 2 =(4x-4)^{\circ}\)
\(\implies m\angle 2 =[4(18)-4]^{\circ}\)
\(\implies m\angle 2 =(72-4)^{\circ}\)
\(\implies m\angle 2 =68^{\circ}\)
Part CAngles on a straight line sum to 180°:
\(\implies m\angle 2 +m\angle 3=180^{\circ}\)
\(\implies 68 ^{\circ}+m\angle 3=180^{\circ}\)
\(\implies m\angle 3=180^{\circ}-68 ^{\circ}\)
\(\implies m\angle 3=112 ^{\circ}\)
A homeowner bought a homeowner's insurance policy. The homeowner pays an annual $650 premium for property coverage with a deductible is $1,175 for each claim. A windstorm causes $42,500 in damages. If a claim for the full amount of damages is approved, how much will the homeowner's insurance company pay for the damages?
$42,500
$41,325
$41,975
$40,825
Answers
Answer:
The homeowner’s insurance company will pay for the damages after the homeowner pays the deductible of $1,175 for each claim. Therefore, the amount that the homeowner’s insurance company will pay for the damages is $42,500 - $1,175 = $41,325.
I hope that helps! (´▽`ʃ♡ƪ)
Step-by-step explanation:
What will be the remainder if x³ 2x² X 1 is divided by x 1?.
Answers
After solving, the reaminder is 1 if x^3-2x^2+X+1 is divided by x-1.
In the given question we have to find the remainder if x^3-2x^2+X+1 is divided by x-1.
The given equation is x^3-2x^2+X+1.
We have to divide this equation by x-1 to find the remainder.
To find the remainder we firstly find the value of x from x-1. Then we put the value of x in the given equation then we can easily find the remainder.
Putting the x-1 equla to zero, so
x=1
Now putting the value of x in the given equation.
=x^3-2x^2+X+1
=(1)^3-2(1)^2+1+1
=1-2+1+1
=1
Hence, the remainder is 1 if x^3-2x^2+X+1 is divided by x-1.
To learn more about division method link is here
brainly.com/question/12520197
#SPJ4
A middle school club is planning a homecoming dance to raise money for the school. Decorations for the dance cost $80, and the club is charging $10 per student that attends.
Which graph describes the relationship between the amount of money raised and the number of students who attend the dance?
graph with the x axis labeled number of students and the y axis labeled amount of money raised and a line going from the point 0 comma negative 80 through the point 2 comma negative 100
graph with the x axis labeled number of students and the y axis labeled amount of money raised and a line going from the point 0 comma negative 80 through the point 2 comma negative 60
graph with the x axis labeled number of students and the y axis labeled amount of money raised and a line going from the point 0 comma 80 through the point 2 comma 60
graph with the x axis labeled number of students and the y axis labeled amount of money raised and a line going from the point 0 comma 80 through the point 2 comma 100
Answers
The graph shows the relationship between the number of students who attend a homecoming dance and the amount of money raised. The graph is a straight line with a slope of $10, passing through the point (0, $80) and another point on the line. The fixed cost for decorations is $80, which is a constant cost that does not depend on the number of students attending the dance. For each additional student that attends the dance, the amount of money raised will increase by $10.
Answer:
y = 10x - 80
Therefore your answer is B, hope this helps! :)
Felipe has a business where he builds and sells birdhouses. To build 12 birdhouses, he needs \large 5\frac{1}{4} meters of wood. During the holiday season, Felipe was asked to make \large 4\frac{1}{2} times the number of birdhouses he usually makes. How many meters of wood does Felipe need to make that many birdhouses?
Answers
Based on the number of birdhouses that Felipe has to build in the holiday season, the meters of wood that Felipe needs would be 23 ⁵/₈ meters
How many meters of wood are needed?First, find out the number of birdhouses Felipe needs to make:
= Normal number of birdhouses x Increase in holiday season
= 12 x 4¹/₂
= 54 birdhouses
The meters of wood he needs are:
= Number of birdhouses to be made / Number of bird houses he usually makes x Meters of wood needed for birdhouses Felipe usually makes
= 54 / 12 x 5¹/₄
= 23 ⁵/₈ meters
Find out more on solving for quantities needed at https://brainly.com/question/2740942
#SPJ1
Find the equation of the axis of symmetry of the following parabola algebraically.
y=-x^2+12x-38
Answers
the independent variable is the one that's squared, namely the "x", that means that the parabola is a vertically opening parabola, so its axis of symmetry will simply be the equation of the vertical line that passes through the vertex, hmmm what's its vertex anyway?
\(\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{-1}x^2\stackrel{\stackrel{b}{\downarrow }}{+12}x\stackrel{\stackrel{c}{\downarrow }}{-38} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right)\)
\(\left(-\cfrac{ 12}{2(-1)}~~~~ ,~~~~ -38-\cfrac{ (12)^2}{4(-1)}\right) \implies \left( - \cfrac{ 12 }{ -2 }~~,~~-38 - \cfrac{ 144 }{ -4 } \right) \\\\\\ (6~~,~~-38+36)\implies (\stackrel{x}{6}~~,~~-2)~\hfill \stackrel{\textit{axis of symmetry}}{x=6}\)
Check the picture below.

A competency test has scores with a mean of 82 and a standard deviation of 2. A histogram of the data shows that the distribution is normal. Between what two values do about 99.7% of the values lie? SHOW YOUR WORK
(statistics)
Answers
Using the Empirical Rule, it is found that 99.7% of the values lie between 76 and 88.
What is the Empirical Rule?
It states that, for a normally distributed random variable:
Approximately 68% of the measures are within 1 standard deviation of the mean.Approximately 95% of the measures are within 2 standard deviations of the mean.Approximately 99.7% of the measures are within 3 standard deviations of the mean.In this problem, we have that:
The mean is of 82.The standard deviation is of 2.99.7% of the values lie within 3 standard deviations of the mean, hence between:
\(82 - 3(2) = 76\)
\(82 + 3(2) = 88\)
To learn more about the Empirical Rule, you can take a look at https://brainly.com/question/24537145
The slope of a line is 2. The y-intercept of the line is -6 Which statements accurately describe how to graph the function?
Locate the ordered pair (0-6). From that point on the graph, move up 2, right 1 to locate the next ordered pair on the line.
Draw a line through the two points.
Locate the ordered pair (0-6). From that point on the graph, move up 2left 1 to locate the next ordered pair on the line
Draw a line through the two points.
Locate the ordered pair (-60). From that point on the graph, move up 2, right 2 to locate the next ordered pair on the line.
Draw a line through the nivo points.
Locate the ordered pair (-60). From that point on the graph, move up 2. left 1 to locate the next ordered pair on the line.
Draw a line through the two points,
Mark this and retum
Save and Exit
Subemt
Answers
Answer: A
Step-by-step explanation:
We know the y intercept is -6 so the first point will be (0,-6) and we also know that the slope is 2/1 so after plotting (0.-6) you will have to go up by two and 1 unit to the right.
Answer:
The answer is A!
Step-by-step explanation:
I just did it and it is right! Have an absolutaly amazing day! :) :) :) :)
A garden has an area of 9 square meters. What is the length of one side of this garden?
Answers
Answer:
It can either be 4 or 5
Step-by-step explanation:
It is because of how 4x5 is equal to 9 so they are both sides.
Give the domain and range of the relation. ((10, 2), (-7. 1), (3,-9). (3.-7)) A domain= (2,-9, 1.-7); range = (10, 3,-7) B) domain (10, 3, -7, -3); range = (2, 9, 1.-7) domain={10, 3, -7); range=(2, -9, 1, -7) (D) domain (10, 3, -7, 13); range=(2, 9, 1.-7) E
Answers
The correct answer is option C. The domain is {10, 3, -7}, and the range is {2, -9, 1, -7}.
The domain of a relation refers to the set of all possible input values or x-coordinates, while the range represents the set of all possible output values or y-coordinates. Given the points in the relation ((10, 2), (-7, 1), (3, -9), (3, -7)), we can determine the domain and range.
Looking at the x-coordinates of the given points, we have 10, -7, and 3. Therefore, the domain is {10, 3, -7}.
Considering the y-coordinates, we have 2, 1, -9, and -7. Hence, the range is {2, -9, 1, -7}.
Thus, option C is the correct answer with the domain as {10, 3, -7} and the range as {2, -9, 1, -7}.
Learn more about domain here
https://brainly.com/question/28135761
#SPJ11
What is the value of x in the right triangle below?
Show your work and round your answer to the nearest hundredth.

Answers
Answer:
\(x = \sqrt{ {28.46}^{2} - {27}^{2} } = \sqrt{80.9716} = 9.00\)
What is the sum of the infinite geometric series?
25 minus 10 plus 4 minus eight fifths plus continuing
The series diverges.
5/2
50/7
125/7
87/5
Answers
The sum of infinite geometric series is
\(25 - 10 + 4 - \frac{8}{5}\)
is \(\frac{125}{7}\)
What is geometric series?
The series where the ratio between the consecutive terms of the series are same is called geometric series.
The sum of infinite geometric series is
\(25 - 10 + 4 - \frac{8}{5}\)
Here
common ratio (r) = \(-\frac{10}{25} = -\frac{2}{5}\)
Here r lies between -1 and 1
So the given geometric series converges
First term is 25
Sum =
\(\frac{25}{1 -(-\frac{2}{5})}\\\\\frac{25}{\frac{5+2}{5}}\\\\\frac{25}{\frac{7}{5}}\\\\\frac{25 \times 5}{7}\\\\\frac{125}{7}\)
To learn more about geometric series, refer to the link-
https://brainly.com/question/24643676
#SPJ4
A teacher claims that the relationship between
number of hours studied for a test and test score can be
described by g(x) = 45 + 9x, where x represents the
number of hours studied. Graph this function
Answers
The graph representing the given function g(x) = 45 + 9x is as drawn in the attachment.
How to draw a Linear Equation Graph?
We are given the equation of line as;
g(x) = 45 + 9x
Where;
x represents the number of hours studied.
g(x) represents the test score
Thus, to plot this graph, we need to input some x values and find their corresponding g(x) values
At x = -10;
g(x) = 45 + 9(-10)
g(x) = -45
At x = -1;
g(x) = 45 + 9(-1)
g(x) = 35
At x = 0;
g(x) = 45 + 9(0)
g(x) = 45
At x = 1;
g(x) = 45 + 9(1)
g(x) = 54
At x = 2;
g(x) = 45 + 9(2)
g(x) = 63
At x = 3;
g(x) = 45 + 9(3)
g(x) = 72
Read more about Linear Equation Graph at; https://brainly.com/question/26148595
#SPJ1

A test of weld strength involves loading welded joints until fracture occurs. For a certain type of weld, 20%
of the fractures occur in the beam rather than in the weld.
a) Calculate the probability that the first fracture in the beam occurs on the third test of weld strength.
b) Determine the mean and variance of the number of tests to find the first fracture in the beam rather than in the weld.
Answers
Therefore, the mean of the number of tests is 5 and the variance is 4 for finding the first fracture in the beam rather than in the weld.
a) To calculate the probability that the first fracture in the beam occurs on the third test of weld strength, we can use the geometric probability formula.
The probability of the first fracture occurring in the beam is 20%, which can be expressed as 0.2. The probability of not fracturing in the beam in the first two tests is (1 - 0.2)^2 = 0.64. The probability of fracturing in the beam on the third test, given that it has not occurred in the first two tests, is 0.2.
Therefore, the probability that the first fracture in the beam occurs on the third test is 0.64 * 0.2 = 0.128, or 12.8%.
b) The number of tests to find the first fracture in the beam follows a geometric distribution. The mean of a geometric distribution is given by 1/p, where p is the probability of success (fracture in the beam).
In this case, p = 0.2 (probability of fracturing in the beam). Therefore, the mean of the number of tests to find the first fracture in the beam is 1/0.2 = 5 tests.
The variance of a geometric distribution is given by (1 - p) / (p^2). In this case, the variance is (1 - 0.2) / (0.2^2) = 4.
To know more about variance,
https://brainly.com/question/14189285
#SPJ11
a force vector points at an angle of 41.5 ° above the x axis. it has a y component of 311 newtons (n). find (a) the magnitude and (b) the x component of the force vector.
Answers
the magnitude of the force vector is approximately 470.41 N, and the x component of the force vector is approximately 357.98 N.
(a) The magnitude of the force vector can be found using the given information. The y component of the force is given as 311 N, and we can calculate the magnitude using trigonometry. The magnitude of the force vector can be determined by dividing the y component by the sine of the angle. Therefore, the magnitude is given by:
Magnitude = y component / sin(angle) = 311 N / sin(41.5°)
Magnitude = y component / sin(angle)
Magnitude = 311 N / sin(41.5°)
Magnitude ≈ 470.41 N
(b) To find the x component of the force vector, we can use the magnitude and the angle. The x component can be determined using trigonometry by multiplying the magnitude by the cosine of the angle. Therefore, the x component is given by:
x component = magnitude * cos(angle)
x component = magnitude * cos(angle)
x component = 470.41 N * cos(41.5°)
x component ≈ 357.98 N
Learn more about force vector here:
brainly.com/question/28969457
#SPJ11
What will your mom’s monthly instalments be if the total amount that she must pay back is R6960? with steps
Answers
The monthly payment is obtained with the following equation:
\(A = 6960\frac{\frac{r}{12}\left(1 + \frac{r}{12}\right)^n}{\left(1 + \frac{r}{12}\right)^n - 1}\)
In which:
r is the interest rate.n is the number of payments.What is the monthly payment formula?The monthly payment formula is defined as follows:
\(A = P\frac{\frac{r}{12}\left(1 + \frac{r}{12}\right)^n}{\left(1 + \frac{r}{12}\right)^n - 1}\)
In which:
P is the initial amount.r is the interest rate.n is the number of payments.For this problem, the lone parameter given is P = 6960, hence the equation is:
\(A = 6960\frac{\frac{r}{12}\left(1 + \frac{r}{12}\right)^n}{\left(1 + \frac{r}{12}\right)^n - 1}\)
In which:
r is the interest rate.n is the number of payments.Missing InformationThe problem is incomplete, hence the formula used to obtain the monthly payment was presented.
More can be learned about the monthly payment formula at https://brainly.com/question/14802051
#SPJ1
how many 6 card hands are there (from a standard deck) with at least 3 kings? (enter an integer without commas)
Answers
There are 73,701 different 6-card hands (from a standard deck) with at least 3 kings.
To calculate the number of 6-card hands with at least 3 K's, the problem can be divided into:
Case 1:
Exactly 3 Kings
There are 4 ways to choose 3 kings to put in the hand, then there are 48 cards left to choose the remaining 3 cards (because we used 3 cards in a 52-card deck). Therefore, the number of 6-card hands with exactly 3 kings is:
4 * (48 choose 3) = 4 * 17,296 = 69,184
Case 2:
Exactly 4 Kings
There are 4 ways to choose 4 kings to put in the hand, then there are 48 cards left to choose the remaining 2 cards. Therefore, the number of 6-card hands with exactly 4 kings is:
4 * (48 choose 2) = 4 * 1.128 = 4.512
Case 3:
Exactly 5 kings
There are 4 ways to choose the 5 kings in the hand, then there is only one card left to choose from (because we used 5 of the 52 cards in the deck of cards). Therefore, the number of 6-card hands with exactly 5 kings is:
4*1=4
Case 4:
6 cards are king
There is only one way to choose all 6 cards as king.
Therefore, the total number of 6-card hands with at least 3 kings is:
69,184 + 4,512 + 4 + 1 = 73.701
So there are 73,701 different 6-card hands with at least 3 kings.
learn more about the deck of cards
brainly.com/question/30519560
#SPJ4
i need to find the vertex for 3x^2 + 2x - 1
