Calculate the area of one triangle so that you can begin building the tabletop .What is the area of each triangle in square inches
Answers
A triangle in which one of the interior angles is 90° is called a right triangle. The longest side opposite to the right angle is the hypotenuse and the two arms of the right angle are the height and the base.
The area of each triangle is 200 square inches.
What is a right triangle?A triangle in which one of the interior angles is 90° is called a right triangle. The longest side opposite to the right angle is the hypotenuse and the two arms of the right angle are the height and the base.
We have,
The area of a right triangle is given by:
= 1/2 x base x height
We have from the figure,
Base = 20 inches
Height = 20 inches
Area = 1/2 x 20 x 20
Area = 10 x 20
Area = 200 square inches
Thus the area of each triangle is 200 square inches.
Learn more about triangles here:
https://brainly.com/question/2773823
#SPJ1
The complete question is:
You work as an assistant to a carpenter who designed the tabletop below. He tells you that each shape is a right triangle, and each is the same size. You now need to calculate the area of one triangle so that you can begin building the tabletop. What is the area of each triangle in square inches?
A. 200 square inches
B. 400 square inches
C. 570 square inches
D. 2,800 square inches
E. 5,600 square inches

Related Questions
the line with a slope of 9/7 & containing a midpoint of the segment whose end points are (2, -3) & (-6, 5)
Answers
1. Find the midpoint of the segment using the midpoint formula:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Midpoint = ((2 + (-6)) / 2, (-3 + 5) / 2)
Midpoint = (-4 / 2, 2 / 2)
Midpoint = (-2, 1)
2. Use the midpoint and the slope to find the equation of the line in point-slope form. The point-slope form is given by:
y - y1 = m(x - x1), where (x1, y1) is the midpoint and m is the slope.
Substituting the values:
y - 1 = (9/7)(x - (-2))
y - 1 = (9/7)(x + 2)
y - 1 = (9/7)x + (18/7)
3. Simplify the equation to obtain the slope-intercept form:
y = (9/7)x + (18/7) + 1
y = (9/7)x + (18/7) + (7/7)
y = (9/7)x + (25/7)
So, the equation of the line with a slope of 9/7 and containing the midpoint of the segment with endpoints (2, -3) and (-6, 5) is y = (9/7)x + (25/7).
Answer:Therefore, the equation of the line with a slope of 9/7 and containing the midpoint of the line segment with endpoints (2, -3) and (-6, 5) is:
y = (9/7)x + 25/7.
Step-by-step explanation:Step 1: Find the midpoint of the line segment.
The midpoint formula is given by:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Given the endpoints of the line segment as (2, -3) and (-6, 5), we can find the midpoint as follows:
Midpoint = ((2 + (-6)) / 2, (-3 + 5) / 2)
Midpoint = (-4 / 2, 2 / 2)
Midpoint = (-2, 1)
So, the midpoint of the line segment is (-2, 1).
Step 2: Write the equation of the line using the slope-intercept form.
The slope-intercept form of a line is given by:
y = mx + b
where m is the slope and b is the y-intercept.
Given the slope as 9/7, we have:
y = (9/7)x + b
Step 3: Substitute the coordinates of the midpoint to find the value of b.
Using the coordinates of the midpoint (-2, 1), we can substitute these values into the equation:
1 = (9/7)(-2) + b
1 = -18/7 + b
To find the value of b, we can solve this equation:
1 + 18/7 = b
25/7 = b
Step 4: Write the final equation of the line.
Using the value of b, the equation becomes:
y = (9/7)x + 25/7
An office manager orders one calculator or one calendar for each of the office's 60 employees. Each calculator costs $15, and each calendar costs $10. The entire order totaled $800.
Part A: Write the system of equations that models this scenario. (5 points)
Part B: Use substitution method or elimination method to determine the number of calculators and calendars ordered. Show all necessary steps. (5 points)
Answers
The system of equations is.
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
And the solutions are y = 50 and x = 10.
How to write and solve the system of equations?Let's define the two variables:
x = number of calculators.y = number of calendars.With the given information we can write two equations, then the system will be:
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
Now let's solve it.
We can isolate x on the first to get:
\(\text{x} = 60 - \text{y}\)
Replace that in the other equation to get:
\(15\times(60 - \text{y}) + 10\text{y} = 800\)
\(-2\bold{y} = 900 - 800\)
\(-2\bold{y} = 100\)
\(\text{y} = \dfrac{100}{-2} = \bold{50}\)
Then \(\bold{x=10}\).
Therefore, the solutions are y = 50 and x = 10.
Learn more about systems of equations at:
https://brainly.com/question/31812807
The graph of a rational function f is shown below.
Assume that all asymptotes and intercepts are shown and that the graph has no "holes".
Use the graph to complete the following.


Answers
We have y+2 = 0 and x - 2 = 0. The provided function has an x and y-intercept of -2 and +2, respectively. There is no vertical asymptote. Two is the horizontal asymptote.
What is a graph?A diagram depicting the relationship between two or more variables, each measured along with one of a pair of axes at right angles.
The y-intercept of a function is determined by the intersection of its graph with the y-axis. The value of y on the y-axis at which the considered function crosses it is called the y-intercept.
Assume the following equation: y = f (x)
We have x =0- 2 and y+2 = 0,The x and y intercept of the given function is -2 and +2.
The vertical asymptote is none. The horizontal asymptote is 2.
Hence,we have y+2 = 0 and x - 2 = 0. The provided function has an x and y-intercept of -2 and +2, respectively. There is no vertical asymptote. Two is the horizontal asymptote.
To learn more about the graph, refer to the link;
https://brainly.com/question/14375099
#SPJ1
Two situations are shown below: 1. Charlie has 3 times as many baseball cards as Ramon. If Ramon has x number of basebal cards how many does Charte have? 2. Emily has 3 more bracelets than Amy. If Amy has x number of bracelets, how many does Emily have Are these situations represented by the same expression? Explain why or why not
Answers
Case 1:
Three time a number expresses a multiplication: three times X is
3X
Case 2:
Three more than a number expresses an addition: three unities more than X is
X + 3
They are not the same expression. One is an addition and the other is a multiplication. If x = 5, in the first, 3x = 15, in the second x + 3 = 8
They are not the same
Enid jogs on a treadmill for exercise. Each time she finishes jogging, the treadmill will report the number of calories she burned. Enid claims that the distance she jogs and the number of calories she burns are in a proportional relationship. Data from her last four jogs are shown.
HELP QUICK

Answers
The correct statement is: She should calculate the ratio between the number of calories she burned versus the number of miles she ran.
What is a ratio?The quantitative relation between two amounts shows the number of times one value contains or is contained within the other. for example-"the ratio of computers to students is now 2 to 1"
Given here: The table containing data calories vs miles run.
You can tell if a table shows a proportional relationship by calculating the ratio of each pair of values. If those ratios are all the same, the table shows a proportional relationship.
Thus calculating the ratio for each pair of entries we get
1) ratio=118/1.2
=295:3a or unit rate 98.33 calories per mile
2) 190/2= 95:1 or unit rate 95 calories per mile
3) 226/2.4=565:6 or unit rate94.1
clea,rly the ratios are different.
Hence, The table containing the data doesn't form a proportional relationship.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ1
Determine whether or not the given procedure results in a binomial distribution. If not, identify which condition is not met. Rolling a six-sided die 80 times and recording the number of l's rolled, Answer Tables Yes AN No There are more than two possible outcomes on each trial of the experiment. The experiment does not consist of n identical trials. The trials are dependent
Answers
Rolling a six-sided die 80 times and recording the number of l's rolled and it is a Binomial Distribution.
The binomial distribution is a probability distribution used in statistics that summarizes the probability that a value will take on one of two independent values given a set of parameters or assumptions. The binomial distribution is calculated by multiplying the probability of success by the power of the number of successes and by multiplying the probability of failure by the power of the difference between the number of successes and the number of trials. The product is then multiplied by the combination of trials and successes.
For example, suppose a casino develops a new game where participants bet on the number of heads or tails in a specified number of coin tosses. Suppose a contestant wants to bet $10 that 20 coin tosses will result in exactly 6 heads. The participants wanted to calculate the probability of this happening, so they used calculations from the binomial distribution.
The probability is calculated as :
(20! / (6! × (20 - 6)!)) × (0.50)⁶ × (1 - 0.50)⁽²⁰⁻⁶⁾. Therefore, the probability of getting exactly 6 heads out of 20 coin tosses is 0.037, or 3.7%.
In this case, the expected value is 10 heads, so the contestant made a bad bet.
Learn more about Binomial Distribution:
https://brainly.com/question/31197941
#SPJ4
please I need help with this

Answers
A. The following are sets A and B:
A = {2, 3, 5, 7, 11}
B = {1, 2, 3, 4, 6, 12}
C. Elements not in A or A' = ∅
B. The Venn diagram is attached
How to solve sets?A universal set is a set which consists of all elements related to the given sets. It is denoted by U.
A. Set A:
A = {2, 3, 5, 7, 11}
Set B:
B = {1, 2, 3, 4, 6, 12}
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
A' = {1, 4, 6, 8, 9, 10, 12}
C. Elements not in A or A' = ∅
Complement of set A is refers to a set that contains the elements present in the universal set but not in set A.
Hence, the Venn diagram of sets A, B and U has been attached.
Read more on set theory:
https://brainly.com/question/13458417
#SPJ1

An interior designer is redecorating a room that is 26 feet long by 18 feet wide by 9 feet high. At one end of the room is a door that is 6 feet 6 inches high and 4 feet wide. One of the walls contains 2 windows, each of which is 2 feet wide by 2 feet 6 inches high.
A: How much will it cost to carpet the floor if the carpet sells for $18.00 a square yard? $
B: How much will it cost to wallpaper all four walls if wallpaper costs $0.75 per square foot? $
C: How much will it cost to paint the ceiling using paint that sells for $25 per gallon if a quart of paint will cover 88 square feet? $
D: What will be the cost of the entire project? $
Answers
Answer: A: It will cost $936.00 to carpet the floor.
B: It will cost $297.00 to wallpaper all four walls.
C: It will cost $33.25 to paint the ceiling.
D: The cost of the entire project will be $1266.25.
Step-by-step explanation:
To calculate the costs for carpeting, wallpapering, painting, and the overall cost of the project, we need to determine the areas that need to be covered and the corresponding prices for each material.
Given dimensions:
Room length: 26 feet
Room width: 18 feet
Room height: 9 feet
Door dimensions:
Height: 6 feet 6 inches
Width: 4 feet
Window dimensions (each):
Width: 2 feet
Height: 2 feet 6 inches
A: Carpeting the floor:
To find the area of the floor, we multiply the length and width of the room:
Floor area = Length × Width = 26 feet × 18 feet = 468 square feet.
To convert to square yards (since the carpet is sold per square yard), we divide by 9:
Floor area in square yards = 468 square feet / 9 = 52 square yards.
Cost to carpet the floor = Floor area in square yards × Cost per square yard = 52 square yards × $18.00 = $936.00.
B: Wallpapering the walls:
To find the area of the walls, we calculate the perimeter of the room (2 × (Length + Width)) and multiply it by the height of the room:
Wall area = Perimeter × Height = 2 × (26 feet + 18 feet) × 9 feet = 396 square feet.
Cost to wallpaper the walls = Wall area × Cost per square foot = 396 square feet × $0.75 = $297.00.
C: Painting the ceiling:
To find the area of the ceiling, we multiply the length and width of the room:
Ceiling area = Length × Width = 26 feet × 18 feet = 468 square feet.
Since a quart of paint covers 88 square feet, we need to determine the number of quarts required:
Number of quarts = Ceiling area / Coverage per quart = 468 square feet / 88 square feet = 5.32 quarts.
Since a gallon contains 4 quarts, the number of gallons required is 5.32 quarts / 4 quarts = 1.33 gallons.
Cost to paint the ceiling = Number of gallons × Cost per gallon = 1.33 gallons × $25.00 = $33.25.
D: Cost of the entire project:
Total cost = Cost to carpet the floor + Cost to wallpaper the walls + Cost to paint the ceiling
= $936.00 + $297.00 + $33.25 = $1266.25.
Therefore:
A: It will cost $936.00 to carpet the floor.
B: It will cost $297.00 to wallpaper all four walls.
C: It will cost $33.25 to paint the ceiling.
D: The cost of the entire project will be $1266.25.
For more questions on cost
https://brainly.com/question/13574768
#SPJ11
To make marbled paper, Shannon filled a rectangular 279/10cm by 178/10cm dish with water. Then they gently swirled paint on top of the water. let a represent the area of the dish.
Select 1 multiplication and 1 division equation to represent the relationship.
choose 2 answers
A) 178/10 x a = 279/10
B) 178/10 x 279/10 = a
C) 279/10 ÷ 178/10 = a
D) a ÷ 178/10 = 279/10
Answers
The area of the dish, a, can be represented by the product of its length and width. Thus, we can write:
a = (279/10) cm x (178/10) cm
Simplifying this expression, we get:
a = 4953/100 cm^2
So, the correct equations are:
B) 178/10 x 279/10 = a
and
D) a ÷ 178/10 = 279/10
Use the bar chart to work out which of these conclusions are true.
- The profit generally decreased.
- The profit was highest in December.
- There were two months where the profit was £300.
- The total profit was under £2000.

Answers
The conclusions that are true based on the bar chart are:
The profit generally decreased, the profit was highest in December, the total profit was under £2000.
To determine which of the conclusions are true, let's analyze the given bar chart representing profits over several months.
Looking at the bar chart, we observe that the income and expenditure are displayed on a scale ranging from £0 to £1500. The months are labeled along the x-axis, and the profit is represented by the difference between income and expenditure for each month.
First, let's evaluate the conclusions:
The profit generally decreased: From the chart, we can see that the profit indeed decreased over time. The bars show a general downward trend, indicating a decrease in profit.
The profit was highest in December: December has the tallest bar among all the months, indicating that the profit was highest in that month. Therefore, this conclusion is true.
There were two months where the profit was £300: To verify this, we examine the bars for a height of £300. Based on the chart, we can only identify one month, which appears to be August, where the profit reaches approximately £300. Therefore, this conclusion is false as there is no indication of two months with a profit of £300.
The total profit was under £2000: To determine the total profit, we sum up the heights of all the bars in the chart. By visual estimation, it appears that the sum of the bars is well below £2000. Therefore, this conclusion is likely to be true.
However, the conclusion stating that there were two months where the profit was £300 is not supported by the chart. So, the statements whivch are true are the profit generally decreased, the profit was highest in December, the total profit was under £2000.
For more such questions on bar chart
https://brainly.com/question/30243333
#SPJ8
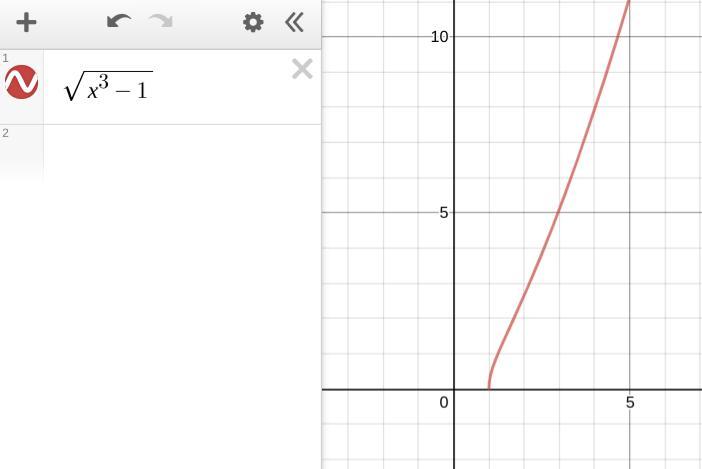
what is the value of x in √x^3-1

Answers
9514 1404 393
Answer:
x ≥ 1
Step-by-step explanation:
The argument of the square root cannot be negative, so the expression is only defined for ...
x³ -1 ≥ 0
x³ ≥ 1 . . . . . add 1
x ≥ ∛1 . . . . cube root
x ≥ 1 . . . . the domain of the expression
_____
As you can see, the graph only exists for x ≥ 1.
Algebra 2
L.6 Evaluate polynomials using synthetic division CHC
If g(y) = 6y? + 8y - 9, use synthetic division to find g(1).
Submit

Answers
The original plan for assigning telephone numbers that you investigated in
Applications Task 4 was implemented in
1947. At that time, the supply of numbers was expected to last for 300 years. However, by the 1970s the numbers were already starting to run out. So, the numbering plan
had to be modified. In this task, you will count the number of different phone numbers that were available in 2012.
a. For three-digit area codes, the first digit cannot be a 0 or a 1. Assuming no additional restrictions, how many three-digit area codes are possible under
this plan?
b. Certain area codes are classified as "Easily Recognizable Codes" (BRCs).
ERCs designate special services, like 888 for toll-free calls. The requirement for an ERC is that the second and third digit of the area code must be the same. The first digit again cannot be a 0 or a 1. How many ERCs are there?
c. Consider the seven digits after the area code. As with the area code, the first digit of the three-digit local prefix cannot be a 0 or a 1. The remaining six digits for the local number have no restrictions. How many of these seven-digit phone numbers are possible?
d. Assuming only the 0 and 1 restrictions in Parts a and c, how many ten-digit phone numbers are possible?
Answers
a. Assuming no additional restrictions, there are 800 possible three-digit area codes.
b. Considering ERCs, there are 80 ERCs.
c. For the seven digits after the area code, there are \(8 \times 10^6 = 8,000,000\) possible seven-digit phone numbers.
d. Assuming only the 0 and 1 restrictions from parts a and c, the number of possible ten-digit phone numbers is 800 \(\times\) 8,000,000 = 6,400,000,000.
a. For three-digit area codes, the first digit cannot be 0 or 1.
Assuming no additional restrictions, there are 8 possibilities for the first digit (2-9) and 10 possibilities for each of the remaining two digits (0-9). Therefore, the total number of three-digit area codes possible under this plan is \(8 \times 10 \times 10 = 800.\)
b. For an ERC (Easily Recognizable Code), the second and third digits of the area code must be the same, and the first digit cannot be 0 or 1. There are 8 possibilities for the first digit (2-9) and 10 possibilities for the third digit (0-9).
Since the second digit must be the same as the third digit, there is only 1 possibility.
Therefore, the total number of ERCs is \(8 \times 1 \times 10 = 80.\)
c. For the seven digits after the area code, the first digit of the three-digit local prefix cannot be 0 or 1.
There are 8 possibilities for the first digit (2-9) and 10 possibilities for each of the remaining six digits (0-9).
Therefore, the total number of seven-digit phone numbers possible is 8 * \(10\times 10 \times 10 \times 10 \times 10 \times 10 = 8,000,000.\)
d. Assuming only the 0 and 1 restrictions from parts a and c, the number of possible ten-digit phone numbers can be calculated by multiplying the number of possibilities for each digit position.
For the area code (part a), there are 800 possibilities.
For the seven digits after the area code (part c), there are 8,000,000 possibilities.
Therefore, the total number of ten-digit phone numbers possible is 800 * 8,000,000 = 6,400,000,000.
For similar question on area codes.
https://brainly.com/question/29279031
#SPJ8
a water snake in a well is 30 M below the ground level its lights 20 m upward and then slips down 10 M how far it is from the ground level
\( - 30 - + 20 - - 10\)
Answers
If the water snake is initially 30 meters below the ground level and then climbs 20 meters upward, it will be 30 - 20 = 10 meters below the ground level. However, if it then slips down 10 meters, it will be 10 + 10 = 20 meters below the ground level.
What is the value of the digit in the ones place?
2,615
A. 50
B. 5
OC. 2,000
OD. 100
Answers
Brainliest to right answer

Answers
8j-k+14
8(.25)-1+14
2-1+14
1+14
15
Answer:
The answer is 15.
Step-by-step explanation:
can someone help PLS? its Surface Area of Composite Shapes

Answers
The total surface area of the figure is 315π square feet, or approximately 988.8 square feet if we use a value of 3.14 for π.
Given information:
The cylinder is sitting on the base of the cone.
The diameter of the base is 14 feet.
The slant height of the cone is 9 feet and the height of the cylinder is 11 feet.
To find the total surface area of the figure, we need to find the surface area of the cone and the surface area of the cylinder and add them together.
The surface area of the cone:
The radius of the cone is half of the diameter, which is 7 feet.
The lateral surface area of the cone can be found using the formula:
L = πrs, where r is the radius and s is the slant height.
L = π(7)(9) = 63π square feet
The base of the cone is a circle with a radius of 7 feet, so its area is:
A = πr² = π(7²) = 49π square feet
The surface area of a cylinder:
The radius of the cylinder is also 7 feet since it shares the same base as the cone.
The lateral surface area of the cylinder is:
L = 2πrh, where r is the radius and h is the height.
L = 2π(7)(11) = 154π square feet
The base of the cylinder is another circle with a radius of 7 feet, so its area is:
A = πr² = π(7²) = 49π square feet
Total surface area:
Adding the lateral surface area and the base area of the cone and cylinder, we get:
63π + 49π + 154π + 49π = 315π square feet
To learn more about the cylinder;
https://brainly.com/question/16134180
#SPJ1
Calculate each compound event probability: a. X ≤ 15, n = 20, π = .70 (Round your answer to 4 decimal places.) b. X > 8, n = 11, π = .65 (Round your answer to 4 decimal places.) c. X ≤ 1, n = 13, π = .40 (Round your answer to 4 decimal places.)
Answers
For X ≤ 15, n = 20, π = .70 ; compound event probability is approximately 0.0008 .
For X > 8, n = 11, π = .65 ; compound event probability is approximately 0.9198.
For X ≤ 1, n = 13, π = .40 ; compound event probability is approximately 0.6646 .
a. To calculate the probability of the event X ≤ 15, n = 20, π = .70, we will use the binomial distribution formula:
P(X ≤ 15)
= ∑_(k=0)¹⁵〖(20Ck)(0.70)^k (0.30)^(20-k) 〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.0008 (rounded to 4 decimal places).
b. To calculate the probability of the event X > 8, n = 11, π = .65, we will first find the probability of X ≤ 8, and then subtract this value from 1 to find the complement probability:
P(X > 8) = 1 - P(X ≤ 8)
= 1 - ∑_(k=0)⁸〖(11Ck)(0.65)^k (0.35)^(11-k)〗
Using a binomial distribution calculator, we can find the probability of X ≤ 8 to be approximately 0.0802.
Therefore, the probability of X > 8 is approximately 0.9198 (rounded to 4 decimal places).
c. To calculate the probability of the event X ≤ 1, n = 13, π = .40, we will use the binomial distribution formula:
P(X ≤ 1)
= ∑_(k=0)¹〖(13Ck)(0.40)^k (0.60)^(13-k)〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.6646 (rounded to 4 decimal places).
For more such questions on event probability visit:
https://brainly.com/question/30390037
#SPJ8
Use algebraic methods to find as many intersection points of the following curves as possible. Use graphical methods to identify the remaining intersection points. R = 6 sin theta and r = 6 cos theta the intersection point(s) is/are_______
(Type an ordered pair. Type exact answer for each coordinate, using phi as needed. Type the coordinate for theta in radians between 0 and phi. Use a comma to separate answers as needed)
Answers
The intersection points are (6, 6) and (-6, -6).
What is Intersection points?
The point at which two lines or curves intersect is referred to as the point of intersection. The point at which two curves intersect is crucial because it is the point at which the two curves take on the same value.
The given curves are the polar equations of two circles with radii 6. To find their intersection points, we can set the two equations equal to each other and solve for Ф.
6 sin(Ф) = 6 cos(Ф)
Dividing both sides by 6 and rearranging terms, we get:
tan(Ф) = 1
This equation has infinitely many solutions, but we are only interested in those that lie in the interval [0, π/2].
Ф = π/4 satisfies this condition and corresponds to the point (6, 6) in Cartesian coordinates.
Since the two curves are circles, they are symmetrical about the origin. Therefore, we can deduce that the other intersection point is (-6, -6).
Therefore, the intersection points are (6, 6) and (-6, -6).
To know more about Intersection points visit,
https://brainly.com/question/29248863
#SPJ4
Can somebody please help me!!!!

Answers
Answer:
first is 180
second is 270
third is 90
Answer:
Step-by-step explanation:

A triangle with area 184 square inches has a height that is two less than six times the width. Find the height and the width of the triangle.
Answers
The height of the triangle is √(115) - 1 inches and the width is (1 + √(115)) / 6 inches.
Let's begin by assigning variables to the height and width of the triangle. We'll use h for height and w for width.
From the problem statement, we know that the area of the triangle is 184 square inches:
Area = (1/2) * base * height
where the base is equal to the width. We can rearrange this formula to solve for the height:
height = 2 * Area / base
Since the area is given as 184 square inches and the base is equal to the width, we can write:
h = 2 * 184 / w
We also know that the height is two less than six times the width. Writing this as an equation, we have:
h = 6w - 2
Now we can substitute the expression for h from the second equation into the first equation:
2 * 184 / w = 6w - 2
Multiplying both sides by w gives:
2 * 184 = w * (6w - 2)
Expanding the right side gives:
2 * 184 = 6w² - 2w
Simplifying further gives:
6w² - 2w - 368 = 0
This is a quadratic equation that we can solve using the quadratic formula:
w = (-b ± √(b² - 4ac)) / 2a
where a = 6, b = -2, and c = -368. Plugging in these values gives:
w = (2 ± √(2² - 4 * 6 * (-368))) / 2(6)
Simplifying further gives:
w = (1 ± √(115)) / 6
Taking the positive value gives:
w = (1 + √(115)) / 6
Plugging this value back into either equation for h gives:
h = 6w - 2 = 6((1 + √(115)) / 6) - 2 = 1 + √(115) - 2 = √(115) - 1
To learn more about height and the width click on,
https://brainly.com/question/27948071
#SPJ1
what is 32.7 + 21.63
Answers
Answer:
54.33
Step-by-step explanation:
Answer:
54.33
Step-by-step explanation:
Addition or a calculwtor can be used
Question 4 of 40
Which of these is a correct expansion of (3x-2)(2x2+5)?
OA. 3x 2x2 + 3x 5+2 2x² +2.5
B. 3x 2x2 + 3x.5+ (-2) 2x2 + (-2).5
O C. 3x 2x²+(-2) 2x² + 2x².5+ (-2).5
SUBMIT
Answers
Answer:
3x* 2x^2 +3x*5 -2 * 2x^2 -2 *5
Step-by-step explanation:
(3x-2)(2x^2+5)
We can FOIL to find the expansion
First 3x* 2x^2 = 6x^3
Outer 3x*5 = 15x
Inner -2 * 2x^2 = -4x^2
Last -2 *5 = -10
Add all the terms together
3x* 2x^2 +3x*5 -2 * 2x^2 -2 *5
Answer:
3x • 2x^2 + 3x • 5 + (–2) • 2x^2 + (–2) • 5
Step-by-step explanation:
other answer was right
Presbycusis is the gradual hearing loss that occurs as a person ages. An estimated one-quarter of Americans between the ages of 65 and 75 and three-quarters of those older than 75 have some degree of hearing loss.
An audiologist is interested in the efficacy of three different types of hearing aids. He gathers three groups of hearing-impaired clients: One group receives analog hearing aids, which convert sound waves into amplified electrical signals. The second group receives digital hearing aids, which use directional microphones to control the flow of sound and convert the sound waves into numerical codes before amplifying them. The third group receives cochlear implants. The results come in, and a statistician conducts an analysis of variance.
The _____________ is that there is no difference between the population means (in other words, there is no treatment effect).
The ____________ is that at least one of the population means is different from another (in other words, there is an effect of at least one of the treatments).
Answers
Answer:
The answer is the "Null hypothesis and Alternative hypothesis".
Step-by-step explanation:
The null hypothesis is almost like a hypothesis test, which indicates the certain demographic characteristics which aren't varied.
The alternative presumption will be that the hypothesis besides making predictions is opposite to the void assumption. Its posts are generally taken as a result of a meaningful effect.
Difference:
The null hypothesis is indeed a gross generalization, which specifies there is no relation between different phenomenons under evaluation. There is no association between the two groups. An alternate solution hypothesis is a statement, that defines there is a relation between different chosen variables in this study.
A system of equations is given.
Equation 1: 4x − 6y = 10
Equation 2: 9x + 2y = 7
Explain how to eliminate x in the system of equations.
Answers
Step-by-step explanation:
To eliminate x in the system of equations:
1. Multiply Equation 1 by 9 and multiply Equation 2 by -4, this gives:
Equation 1: 36x -54y = 90
Equation 2: -36x - 8y = -28
2. Add the two equations together to eliminate x:
(36x - 54y) + (-36x - 8y) = 90 - 28
Simplifying, we get:
-62y = 62
3. Solve for y:
y = -1
4. Substitute y = -1 into one of the original equations, say Equation 1:
4x - 6(-1) = 10
Simplifying, we get:
4x + 6 = 10
5. Solve for x:
4x = 4
x = 1
Therefore, the solution to the system of equations is x = 1 and y = -1. We can check that these values are correct by substituting them back into the original equations and verifying that they satisfy both equations.
At the start of Kerin's diet he weighed 13 stone 12 pounds. Three months later he weighed 12 stone 10 pounds. There are 14 pounds in a stone. Calculate the reduction in Kerins weight as a percentage of his inetial weight.
Answers
Beginning of diet, 13 stone 12 pounds
13(14) + 12 = 194
Three months later, 12 stone 10 pounds
12(14) + 10 = 178
He lost 16 pounds in 3 months
I'm not really sure what the percentage would be, but it might be 16%
Please if you know the answer tell me it and the steps also thank you.

Answers
Step-by-step explanation: Well to begin, you take 15$ and multiply it by 4, since he wants to buy 4 of those tickets, which is 60$. Then, take the 10$ and multiply it by 2 since he wants 2 of those tickets, which is 20$, you then apply 10% to 60 and 20 by taking 10 percent of 60, then adding it to 60 once have that, which is 66, you take the 3% and find 3% of 66, then add the answer of that to 66, which is 67.98$, you then do the same thing to the 20$.
Sorry if this didnt help, im sure it didnt because im a very bad explainer, but i tried..
There are 180 gorillas at the zoo. If 5% are friendly, how many FRIENDLY
gorillas are at the zoo
Answers
Answer:
A whopping 9 friendly gorillas
Step-by-step explanation:
5% turned into a decimal is 0.05
180*0.05=9
What’s the correct answer answer asap for brainlist

Answers
Answer:
B
Step-by-step explanation:
Musicologists generally define the Classical period of music as ranging from 1730 to 1820. Classical era music followed the late Baroque period of music.
Suppose a normal distribution has a mean of 50 and a standard deviation of 3. What is P(x≤ 44)? A. 0.025 B. 0.975 C. 0.84 D. 0.16
Answers
A normal distribution has a mean of 50 and a standard deviation of 3 , the probability P(X ≤ 44) = P(Z ≤ -2) = 0.0241 option a) 0.025.
In probability theory, normal distribution is also known as Gaussian distribution. It is a probability distribution that is symmetrical, bell-shaped, and a continuous probability distribution. It's also a part of continuous probability distribution that describes real-valued random variables whose probability density function is affected by two parameters: the mean μ and the variance σ².
Let us consider the problem. Suppose a normal distribution has a mean of 50 and a standard deviation of 3. Firstly, we need to standardize the random variable X that is to convert it to the standard normal distribution. We use the following formula for this Z = (X - μ) / σwhere X is the random variable and μ is the mean, σ is the standard deviation of the population.
So in this case, we can write this as Z = (44 - 50) / 3 = -2
We have now obtained the standard score or standard deviation for the random variable X.
Now we need to calculate the probability P(X ≤ 44) = P(Z ≤ -2).
The probability of Z being less than -2 is denoted by the area under the standard normal curve to the left of Z = -2.
Using the standard normal table we look for the probability that corresponds to -2 and the closest we find is 0.0228.
This probability represents the area under the standard normal distribution to the left of Z = -2.
To calculate the area to the left of Z = -2, we add the area to the left of the next integer, which is -3, which we find from the standard normal table as 0.0013, 0.0228 + 0.0013 = 0.0241.
Therefore, the probability P(X ≤ 44) = P(Z ≤ -2) = 0.0241 or 0.025 (rounded to three decimal places)Therefore, the answer is option A. 0.025.
Know more about normal distribution here:
https://brainly.com/question/4079902
#SPJ8