A sixth-grade class collected data on the number of siblings in the class. Here is the dot plot of the data they collected.
How many students had zero brothers or sisters?

Answers
By probability, The number of students who had zero brothers or sisters is 1.
What are examples and probability?
The potential of any random event's result is referred to as probability. To determine the likelihood that any event will occur is the definition of this phrase.
How likely is it that we'll obtain a head when we toss a coin in the air, for instance? Based on how many options are feasible, we can determine the answer to this question.
The probability of students with zero brothers or sisters is calculated from the ratio of the total number of students to the number of students with zero brothers or sisters.
Total number of students = 65
Number of zero siblings = 1
The probability = 1 / 65
So based on this information, we can conclude that in the sixth-grade class and based on the collected data, the number of students who had zero brothers or sisters is 1.
Learn more about Probability
brainly.com/question/30034780
#SPJ1
Related Questions
Suppose the future value of a \( 7.75 \% \) simple interest loan is \( \$ 1,321.17 \) at the end of 230 days. Find the present value of the loan. State your result to the nearest penny.
Answers
The present value of the loan is found to be approximately $70.28.
To find the present value of a loan, we can use the formula:
Present Value = Future Value / (1 + (interest rate * time))
Given that the future value is $1,321.17, the interest rate is 7.75%, and the time is 230 days, we can plug in these values into the formula:
Present Value = 1321.17 / (1 + (0.0775 * 230))
Calculating the expression in the parentheses first:
Present Value = 1321.17 / (1 + 17.8075)
Simplifying further:
Present Value = 1321.17 / 18.8075
Evaluating the division:
Present Value ≈ $70.28
Therefore, the present value of the loan is approximately $70.28.
Know more about the present value
https://brainly.com/question/30390056
#SPJ11
What is the measure of angle B in this triangle?
Enter your answer in the box.

Answers
Answer:
22 degrees
Step-by-step explanation:
Sum of all three angles of a triangle equal 180 degrees so we can add these angles and set it equal to 18” degrees to find x
x+16+120+x=180
2x+136=180
-136. -136
2x=44
/2. /2
x=22
So angle b is 22 degrees
Hopes this helps please mark brainliest
If the variable h represents how many hours samantha works, write an algebraic expression that describes how much
samantha earns if she makes $14. 55 an hour. Create another an real life algebraic expression (or equation). Choose and define your variable
Answers
The algebraic expression that describes how much Samantha earns after h hours if she makes $14.55 an hour is x = $14.55h, where x is the amount of money she earns and h is the number of hours she works.
An algebraic expression is the combination of numbers and variables in expressing and solving a particular mathematical question.
If Samantha makes $14.55 an hour, and h is the number of hours she works, then the algebraic expression to demonstrate how much she earns is:
x = $14.55h
where x = amount of money she earns
h = number of hours she works
Another real life situation:
A piggy bank contains $25, and $1.50 is added each day. The algebraic expression to demonstrate how much money the piggy bank contains is:
m = $25 + $1.50(d)
where m = amount the piggy bank contains after d days
d = number of days
Learn more about algebraic expression here: https://brainly.com/question/4344214
#SPJ4
Find \( a_{1} \) and \( d \) for the following arithmetic series. \[ S_{16}=272, a_{16}=32 \]
Answers
The first term of the arithmetic series is \( a_1 = 2 \) and the common difference is \( d = 2 \).
To find \( a_1 \) and \( d \) for an arithmetic series, we can use the formulas for the \( n \)-th term and the sum of an arithmetic series.
The formula for the \( n \)-th term of an arithmetic series is given by:
\[ a_n = a_1 + (n-1)d \]
where \( a_n \) is the \( n \)-th term, \( a_1 \) is the first term, \( d \) is the common difference, and \( n \) is the position of the term.
Given that \( S_{16} = 272 \) and \( a_{16} = 32 \), we can use the formula for the sum of an arithmetic series to find \( a_1 \) and \( d \).
The formula for the sum of the first \( n \) terms of an arithmetic series is given by:
\[ S_n = \frac{n}{2}(a_1 + a_n) \]
Substituting the given values into the formula, we have:
\[ 272 = \frac{16}{2}(a_1 + 32) \]
Simplifying, we get:
\[ 272 = 8(a_1 + 32) \]
Dividing both sides by 8, we have:
\[ 34 = a_1 + 32 \]
Subtracting 32 from both sides, we find:
\[ a_1 = 2 \]
Now that we have found \( a_1 \), we can substitute it back into the formula for the \( n \)-th term to find \( d \):
\[ a_{16} = a_1 + (16-1)d \]
Substituting the given values, we have:
\[ 32 = 2 + 15d \]
Simplifying, we find:
\[ 30 = 15d \]
Dividing both sides by 15, we get:
\[ d = 2 \]
Therefore, the first term of the arithmetic series is \( a_1 = 2 \) and the common difference is \( d = 2 \).
Learn more about arithmetic series here
https://brainly.com/question/24295771
#SPJ11
Determine the intercepts of the line.
Do not round your answers.
y=6x+13y=6x+13
Answers
Answer: X= -2.1667 Y= 13
PLEASE HELP!! I NEED THESE BONUS POINTS!! If you do answer plz answer all of them. Thank you! I will choose brainiest ;)

Answers
Answer:
7-9 you need to plug numbers into the formula y= mx+b where you plug the plots in M and B.
Step-by-step explanation:
I don't have a graph to plot 1-3 on but all you need to do is plot them and answer if they are parallel, perpendicular, or neither. (The property extends to other related geometric objects. A line is said to be perpendicular to another line if the two lines intersect at a right angle.) (In math, parallel means two lines that never intersect — think of an equal sign.) And if they don't fit either then its NEITHER
Abigail gathered data on different schools' winning percentages and the average yearly salary of their head coaches (in millions of dollars) in the years
2000
20002000-
2011
20112011. She then created the following scatterplot and regression line.
The fitted line has a slope of
8.42
8.428, point, 42.
Answers
If the "fitted-line" has a slope of 8.42, then the correct interpretation is (c) On average, each 1 million dollar increase in salary is linked with 8.42 point increase in the "winning-percentage".
The "Slope" of the "fitted-line" represents the change in the response variable (winning percentage) for each unit increase in the predictor variable (salary of head coach, in millions of dollars).
In this case, the slope is 8.42, which means that on average, for every 1 million dollar increase in salary, there is an associated increase of 8.42 points in winning percentage.
Therefore, Option (c) is the correct interpretation of slope.
Learn more about Slope here
https://brainly.com/question/29075872
#SPJ1
The given question is incomplete, the complete question is
Abigail gathered data on different schools' winning percentages and the average yearly salary of their head coaches (in millions of dollars) in the years 2000-2011. She then created the following scatterplot and regression line.
The fitted line has a slope of 8.42.
What is the best interpretation of this slope?
(a) A school whose head coach has a salary of $0, would have a winning percentage of 8.42%,
(b) A school whose head coach has a salary of $0, would have a winning percentage of 40%,
(c) On average, each 1 million dollar increase in salary was associated with an 8.42 point increase in winning percentage,
(d) On average, each 1 point increase in winning percentage was associated with an 8.42 million dollar increase in salary.

Westin Trading normally nets $6 million per month. The table shows the variance from the average for five months.
Sales Above/Below Average (Millions)
April
May
June
July
Aug.
–2.5
Negative 2 and one-half
3.1
–1.6
2 and two-thirds
Which comparison is true? Use the number line to help.
A number line going from negative 6 to positive 6 in increments of 1.
June < August
April = May
May > July
May = August
Answers
The comparison of variance that is true for the given average per month is "May > July".
What is variance?Variance is a metric for gauging how dispersed a set of data is. The average of the squared discrepancies between each data point and the data set mean is used to compute it. Data points with a high variation are dispersed throughout a wider range of values, whereas those with a low variance are grouped more closely together. In statistics, variability is frequently used to examine data distribution and contrast the variability of various data sets. It is frequently stated in terms of the original data's square units, such square metres or square dollars.
From the given table the average per month is:
April: $6 million - $2.5 million = $3.5 million below average
May: $6 million - $2 million = $4 million below average
June: $6 million + $3.1 million = $9.1 million above average
July: $6 million - $1.6 million = $4.4 million below average
August: $6 million + $2.67 million = $8.67 million above average
Thus, comparing the numbers on the number line we observe that the average in May is greater than July.
Hence, the comparison that is true is "May > July".
Learn more about variance here:
https://brainly.com/question/16269880
#SPJ1
Answer:
It is AStep-by-step explanation:
please Thanks me
PLEASE HELP. !!!!!!!!!!

Answers
which measure captures the variation in ressponses? multiple choice the frequency distribution the median the mode the standard deviation the mean
Answers
the measure that captures the variation in responses is mean and it is the weighted average
What is the meaning of mean in math?
In mathematics and statistics, the mean refers to the average of a set of values. The mean can be computed in a number of ways, including the simple arithmetic mean (add up the numbers and divide the total by the number of observations), the geometric mean, and the harmonic mean.
learn more about of mean here
https://brainly.com/question/521501
#SPJ4
Given the function f(x)=4x²-14x+12, which of the following expressions is equivalent to f(x)?
Answers
Expressions is equivalent to f(x) is (2x²-7x+6).X-terms and constants should be combined with any other like terms on either side of the equation.
How to find equivalent to f(x)?f(x)=4x²-14x+12
In the first stage, a common factor of 2 is eliminated.
2(2x²-7x+6)
Since the quadratic cannot be factored further, the short answer is:
(2x²-7x+6)
Expressions is equivalent to f(x) is (2x²-7x+6).
X-terms and constants should be combined with any other like terms on either side of the equation. Put the terms in the same order, with the x-term usually coming before the constants. The two formulations are equal if and only if each term in both of them is the same.Two systems of equations are equivalent if they have the same solution.
To learn more about equivalent Expressions refer to:
https://brainly.com/question/24734894
#SPJ1
The equivalent expression to f(x) is (2x2-7x+6). On either side of the equation, X-terms and constants should be combined with any other like terms.
What is meant by equivalent expression?Equivalent expressions are expressions that perform the same function despite their appearance. If two algebraic expressions are equivalent, they have the same value when the same value(s) for the variable are used (s). Equivalent equations are algebraic equations with the same solution or root. An equivalent equation is created by adding or subtracting the same number or expression from both sides of an equation. An equivalent equation is produced by multiplying or dividing both sides of an equation by the same non-zero number.Given
f(x) = 4x² - 14x + 12
In the first stage, a common factor of 2 is eliminated.
(4x² - 14x + 12) / 2
Then we get,
2(2x² - 7x + 6)
Since the quadratic cannot be factored further, the short answer is:
(2x² - 7x + 6)
Expressions is equivalent to f(x) is (2x² - 7x + 6).
To learn more about equivalent Expressions, refer to:
brainly.com/question/24734894
#SPJ1
Is sqrt((x-3)^2) = 3 - x?
1) x is not equal to 3
2) -x|x| > 0
Answers
The statement sqrt((x-3)^2) = 3 - x is true only when x is not equal to 3. Therefore, option 1) "x is not equal to 3" is the correct answer.
When we simplify sqrt((x-3)^2), we get |x-3|, which represents the absolute value of (x-3). On the other hand, the expression 3 - x represents the negation of x subtracted from 3.
For x ≠ 3, both |x-3| and 3 - x can be positive or negative depending on the value of x. They are not always equal to each other.
However, if we consider x = 3, the expression sqrt((x-3)^2) becomes sqrt(0^2) = 0, and 3 - x becomes 3 - 3 = 0. In this case, both sides of the equation are equal.
Therefore, the equation sqrt((x-3)^2) = 3 - x is not true for all values of x. It is true when x is not equal to 3, but false when x = 3.
Regarding option 2) "-x|x| > 0", it is unrelated to the given equation and does not provide any information about the validity of the equation sqrt((x-3)^2) = 3 - x.
Learn more about absolute value here:-brainly.com/question/17360689
#SPJ11
The lifespan of a car battery averages 5 years. Suppose the battery lifespan follows an exponential distribution. What is the probability that the battery lasts more than 3 years
Answers
The probability that battery lasts more than 3 years is \(e^{-0.6 }\).
Parameter of Exponential Distribution
It is given that the average lifespan of the car battery = 5 years
⇒ μ = 5
And, we have to find the probability that the car battery lasts more than 3 years.
Now, the relation between the parameter of exponential distribution, λ and average, μ is given as,
1/ λ = μ
⇒ λ = 1/5
Calculating the Probability
The probability for the car battery to lasts more than 3 years is given by P(N>3). Here, N is the lifespan of the car battery.
P(N>3) = 1 - P(N≤3)
P(N>3) = 1-F(4)
Here, F is the exponential distribution for the lifespan of the car battery.
P(N>3) = 1-(1-e^(-λn))
P(N>3) = \(e^{-3/5}\)
Thus, the required probability is,
P(N>3) = \(e^{-0.6 }\)
Learn more about probability here:
https://brainly.com/question/11234923
#SPJ4
Jessie recently drove to visit her parents who live 240240 miles away. On her way there her average speed was 2525 miles per hour faster than on her way home (she ran into some bad weather). If Jessie spent a total of 88 hours driving, find the two rates.
Answers
Answer:
The speed/rate to her parent's house is x = 75 mph
The speed/rate from her parent's house is y = 50 mph
Step-by-step explanation:
Given;
Distance to her parent's house = 240 miles
Total distance travelled (to and fro) = 240×2 = 480 miles
Total time taken t = 8 hours
On her way there her average speed was 25 miles per hour faster than on her way home (she ran into some bad weather)
Let x and y represent her speed to and from her parent's house respectively.
x = y+25 ......1
The time taken to her parent's house is;
time = distance/velocity
t1 = 240/x = 240/(y+25)
The time taken from her parent's house is;
time = distance/velocity
t2 = 240/y
Total time taken t = t1 +t2
t = 240/(y+25) + 240/y = 8
Solving for y ;
(240y + 240(y+25))/(y^2 +25y) = 8
Cross multiply;
240y + 240y+6000 = 8y^2 + 200y
480y +6000 = 8y^2 + 200y
8y^2 + 200y -480y -6000 = 0
8y^2 - 280y - 6000 = 0
Divide through by 8;
y^2 - 35y - 750 = 0
Solving the quadratic equation;
y = 50
or
y = -15
Velocity cannot be negative, so y = 50mph
From equation 1;
x = y+25
Substituting y =50
x = 50 + 25
x = 75 mph
The speed/rate to her parent's house is x = 75 mph
The speed/rate from her parent's house is y = 50 mph
Can Someone PLEASE HELP ME with this PLEASE!!

Answers
Answer:
480 bees.
Step-by-step explanation:
In the test sample, 10 out of the 50 bees observed (20%) flew west. We can assume that 20% of all bees in the hive fly west.
20% of 2400 is 480.
Suppose that Upper X has a discrete uniform distribution f left-parenthesis x right-parenthesis equals StartLayout left-brace1st Row 1st Column 1 divided by 3, 2nd Column x equals 1,2,3 2nd Row 1st Column 0, 2nd Column otherwise EndLayout A random sample of n equals 39 is selected from this population. Find the probability that the sample mean is greater than 2.1 but less than 2.6. Express the final answer to four decimal places (e.g. 0.9876). The probability is
Answers
Answer:
The probability that the sample mean is greater than 2.1 but less than 2.6 is 0.2236.
Step-by-step explanation:
The random variable X follows a discrete uniform distribution.
The probability mass function of X is:
\(f(x)=\left \{ {{\frac{1}{3}};\ x=1,2,3 \atop {0;\ \text{otherwise}}} \right.\)
Then,
a = 1
b = 3
The mean and standard deviation of the random variable X are:
\(\mu=\frac{b+a}{2}=\frac{3+1}{2}=2\\\\\sigma=\sqrt{\frac{(b-a+1)^{2}-1}{12}}=\sqrt{\frac{(3-1+1)^{2}-1}{12}}=0.8165\)
The sample size is, n = 39.
According to the Central Limit Theorem if we have an unknown population with mean μ and standard deviation σ and appropriately huge random samples (n > 30) are selected from the population with replacement, then the distribution of the sample mean will be approximately normally distributed.
Then, the mean of the sample means is given by,
\(\mu_{\bar x}=\mu\)
And the standard deviation of the sample means is given by,
\(\sigma_{\bar x}=\frac{\sigma}{\sqrt{n}}\)
As n = 39 > 30, the sampling distribution of sample mean of X will follow a Normal distribution approximately.
Compute the probability that the sample mean is greater than 2.1 but less than 2.6 as follows:
\(P(2.1<\bar X<2.6)=P(\frac{2.1-2.0}{0.8165/\sqrt{39}}<\frac{\bar X-\mu_{\bar x}}{\sigma/\sqrt{n}}<\frac{2.6-2.0}{0.8165/\sqrt{39}})\)
\(=P(0.76<Z<4.59)\\\\=P(Z<4.59)-P(Z<0.76)\\\\=1-0.77637\\\\=0.22363\\\\\approx 0.2236\)
Thus, the probability that the sample mean is greater than 2.1 but less than 2.6 is 0.2236.
I NEED HELP ASAP
FIRST TI ANSWER GET BRAINLEST

Answers
Answer:
2nd Option
Step-by-step explanation:
m=6
y=-3
so from equation
y=mx+c
y=6x-3
is the req ...... equation..
Answer: 2nd Option is the answer for this
Step-by-step explanation:
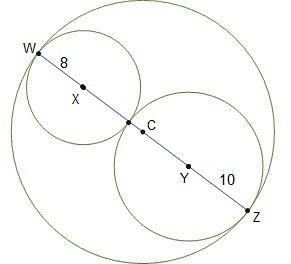
line segment wx is the radius of circle x, and line segment zy is the radius of circle y. points w, x, c, y, and z are all on line segment wz. what is the area of circle c, which passes though points w and z? 81 164 324 1296
Answers
The area of circle C, which passes though points W and Z is 324π square meters.
The center of the outer circle, Point D, is where we want to calculate the area of the circle has a WZ diameter and WC and CZ radii.
That YZ = YD = 10 cm is known.
Let DC = x and CY = 10 - x
The outer circle's radius can be expressed as 8 + 8 + x or 10 + 10 - x, which we can equate to determine its value of x
8 + 8 + x = 10 + 10 - x
Simplify
16 + x = 20 - x
Subtract 16 on both side, we get
x = 4 - x
Add x on both side, we get
2x = 4
Divide by 2 on both side, we get
x = 2
As a result, the circle's radius is
= 8 + 8 + x
= 16 + x
= 16 + 2
= 18 cm
The area of circle = πr²
The area of circle = π(18)²
The area of circle = 324π
Thus, the circle's area is 324π square meters.
To learn more about area of circle link is here
brainly.com/question/28642423
#SPJ4
The complete question is:
Line segment WX is the radius of circle X, and line segment ZY is the radius of circle Y. Points W, X, C, Y, and Z are all on line segment WZ.
What is the area of circle C, which passes though points W and Z?
A. 81
B. 164
C. 324
D. 1296
For which value of x is f(x)=7

Answers
Answer:
5
Step-by-step explanation:
If you input 5 you get 7
Answer: 5
Step-by-step explanation:
f(x) usually means the y-value or output of the functions.
It can find the x value through the graph. When y is 7, you can see that x is 5 (See the image).

What is the percent composition of water in the compound magnesium sulfate heptahydrate, MgDO4•7H2O?
A. 7.3%
B. 24.8%
C. 48.8%
D. 51.2%
Answers
Answer:51. 2%
Step-by-step explanation:
24+32+(16×4)+7(2+16)=24+32+64+126=246
26g of Epsom salt contains 126g of water of crystallisation.Hence, 100g of Epsom salt contains 100×126/246The % of H2O in MgSO4.7H2O=
It is known that x1 and x2 are roots of the equation 3x^2 2x k=0, where 2x1=−3x2. find k.
Answers
Value of the k is -2 for the equation \(3x^{2} +2x + k = 0\).
Given equation is,
\(3x^{2} + 2x + k = 0\)
From the quadratic equation we get,
a = 3, b = 2, c = k
Let us consider roots of the equation are x₁ and x₂
We know that sum of roots is -b/a
x₁ + x₂ = - 2/3
and product of roots is c/a
x₁x₂ = k / 3
It is given that 2x₁ = -3x₂
⇒ x₁ = - 3/2 x₂
Putting value of x₁ in the first equation,
-3/2 x₂ + x₂ = - 2/3
-3x₂ + 2x₂ = -2/3
- x₂ = - 2/3
⇒ x₂ = 2/3
and x₁ = (- 3/2)(2/3)
x₁ = -1
Therefore x₁x₂ = k/3 implies that,
-1(2/3) = k/3
- 2/3 = k/3
k = -2.
To know more about Quadratic equation here,
https://brainly.com/question/19386286
#SPJ4
write an expression in standard form that Is equivalent to 2 + 3(x - 4)
Answers
Answer:
2+3=5(x-4) ,
=5(x-4)
=5x-4
=1x
Solve the simultaneous equations below using substitution.
Y=10x+8
2y+5x=21
Give your answer as an integer or an decimal
Answers
25x=5
x=1/5
DON'T GIVE FAKE ANSWERS OR I'LL REPORT!
What is the area of a sector with a central angle of 45° and a diameter of 5. 6 in. ? Use 3. 14 for π and round your final answer to the nearest hundredth. Enter your answer as a decimal in the box. What is the area of a sector with a central angle of 120° and a radius of 18. 4 m? Use 3. 14 for π and round your final answer to the nearest hundredth. Enter your answer as a decimal in the box
Answers
The area of a sector with a central angle of 45° and a diameter of 5.6 in. is 1.23 square inches.
To see why, you can use the formula for the area of a sector, which is:
A = (θ/360) x π x r^2
where θ is the central angle in degrees, r is the radius, and π is approximately 3.14.
First, you need to find the radius of the sector, which is half of the diameter:
r = d/2 = 5.6/2 = 2.8 in.
Next, you can plug in the values for θ and r into the formula:
A = (45/360) x 3.14 x 2.8^2 = 1.23 square inches
Therefore, the area of the sector is 1.23 square inches.
The area of a sector with a central angle of 120° and a radius of 18.4 m is 1908.57 square meters.
To see why, you can use the same formula for the area of a sector:
A = (θ/360) x π x r^2
First, you need to convert the radius from meters to centimeters, since π is in terms of centimeters:
r = 18.4 m x 100 cm/m = 1840 cm
Next, you can plug in the values for θ and r into the formula:
A = (120/360) x 3.14 x 1840^2 = 1908.57 square meters
Therefore, the area of the sector is 1908.57 square meters.
Which polynomial is in standard form?

Answers
Answer:
Im pretty sure its D
Step-by-step explanation:
draining 15 gallons of water from a fish tank
(Write your answer as an integer)
Answers
Answer:
-15
Step-by-step explanation:
if its just asking for what number would represent a loss of 15 it would be negative 15
i dont know if there's more to the problem or not
Answer:
-15
Step-by-step explanation:
This is because whatever much water was in the tank is now decreasing by 15, therefore, you can write it as -15,
hope this helps!
HURRY WILL MARK YOU BRAINLIEST

Answers
Answer:
x=11/4
Step-by-step explanation:
4x+5=8x-6
4
x
= 8
x
−
1
1 <simplify
-8x -8x
-4x=-11
x=11/4
Evaluate expressions-Match each expression to another expression with the same value

Answers
Answer:
24 / 3
8 x 50
53 x 7
What value of [S] as a fraction of KM, is required to obtain 20% Vmax? [S] equals: a. 0.2 KM b. 0.25 KM c. 0.5 KM d. 0.75 KM e. 0.8.
Answers
The fraction of KM that is required to obtain 20% Vmax is [S] = 0.2 KM.
The Michaelis-Menten equation is given by: V = Vmax[S] / (KM + [S])where, V is the velocity of the reaction, Vmax is the maximum velocity of the reaction,[S] is the substrate concentration, and KM is the Michaelis constant of the enzyme.
Substituting V = 0.2V
max and rearranging the equation,
0.2Vmax = Vmax[S] / (KM + [S])
Multiplying both sides by
(KM + [S]),0.2V
max(KM + [S]) = Vmax[S]
Expanding the equation,
0.2VmaxKM + 0.2Vmax[S]
= Vmax[S]0.2VmaxKM
= 0.8Vmax[S]
Dividing both sides by
Vmax,0.2KM = 0.8[S]
Simplifying the equation,
[S] = 0.2 KM / 0.8[S] = 0.25 KM
Therefore, the fraction of KM that is required to obtain 20% Vmax is [S] = 0.2 KM, which is option (a).
Learn more about velocity from:
https://brainly.com/question/80295
#SPJ11
Deion has a bag of marbles. He has 2 green, 6 blue, 4 red, and 12 yellow marbles.
Deion selects a marble at random. Which of the following statements is true?

Answers
The marble is equally likely to be green, red, or blue as it is to be yellow.