you may need to use the appropriate appendix table to answer this question. suppose that the mean daily viewing time of television is 8.35 hours. use a normal probability distribution with a standard deviation of 2.5 hours to answer the following questions about daily television viewing per household (a) what is the probability that a household views television between 4 and 12 hours a day? (round your answer to four decimal places.) (b) how many hours of television viewing must a household have in order to be in the top 4% of all television viewing households? (round your answer to two decimal places.) hrs (c) what is the probability that a household views television more than 3 hours a day? (round your answer to four decimal places.)
Answers
(a) The probability that a household views television between 4 and 12 hours a day is 0.8864. (b) A household must view at least 12.63 hours of television/day to be in the top 4% of all television viewing households. (c) The probability that a household views television more than 3 hours a day is 0.9830.
(a) To find the probability that a household views television between 4 and 12 hours a day, we need to standardize the values using the formula:
z = (x - μ) / σ
where x is the value we want to find the probability for, μ is the mean, and σ is the standard deviation.
For x = 4 hours:
z = (4 - 8.35) / 2.5 = -1.74
For x = 12 hours:
z = (12 - 8.35) / 2.5 = 1.46
Using a standard normal distribution table or a calculator, we can find the probabilities associated with these z-scores:
P(z < -1.74) = 0.0401
P(z < 1.46) = 0.9265
Therefore, the probability that a household views television between 4 and 12 hours a day is:
P(4 ≤ x ≤ 12) = P(z < 1.46) - P(z < -1.74) = 0.9265 - 0.0401 = 0.8864 (rounded to four decimal places).
(b) To find the number of hours of television viewing a household must have in order to be in the top 4% of all television viewing households, we need to find the z-score that corresponds to the top 4% of the normal distribution:
P(z > z*) = 0.04
Using a standard normal distribution table or a calculator, we can find that the z-score that corresponds to a probability of 0.04 is approximately 1.75.
Using the formula for z-score:
z = (x - μ) / σ
We can solve for x:
x = μ + zσ = 8.35 + 1.752.5 = 12.63 (rounded to two decimal places)
Therefore, a household must view at least 12.63 hours of television per day to be in the top 4% of all television viewing households.
(c) To find the probability that a household views television more than 3 hours a day, we can standardize the value of x = 3 using the formula for z-score:
z = (x - μ) / σ = (3 - 8.35) / 2.5 = -2.14
Using a standard normal distribution table or a calculator, we can find the probability associated with this z-score:
P(z > -2.14) = 0.9830 (rounded to four decimal places).
Therefore, the probability that a household views television more than 3 hours a day is 0.9830.
Learn more about Probability :
https://brainly.com/question/18882393
#SPJ4
Related Questions
Which angle has a negative sine value and a positive cotangent value?

Answers
sin4π/3= sin(π+π/3) = - sinπ/3
cot4π/3=cot(π+π/3)= cotπ/3
OPTION C 4π/3
help me out please explain too please :((

Answers
Answer:
bro I can’t do it TvT
The length of a rectangle is 7 centimeters less than its width. What are the dimensions of the rectangle if its area is 60 square centimeters?
Answers
The dimensions of the rectangle has a width = 12cm and length = 5cm.
Area of rectangleIn calculating the area of a rectangle, we multiply its length and width.
Let us use the letter x to represent the width, so that the length = x - 7
hence we calculate for the unknown x as follows;
x(x - 7) = 60
expand and equate to zero to derive a quadratic equation
x² + 7x - 60 = 0
by factorisation;
x² - 12x + 5x - 60 = 0
x(x - 12) +5(x -12) = 0
(x + 5)(x - 12) = 0
thus for x + 5 = 0
x = -5
and for x - 12 = 0
x = 12
Therefore, x = 12 is true for the quadratic equation and also for the width = 12 and length = 5cm for the rectangle.
Learn more about area here:https://brainly.com/question/25292087
#SPJ1
Please help!
A building is constructed on top of a cliff that is 300 meters high. A person standing on level ground below the cliff observes that the angle of elevation to the top of the building is 72° and the angle of elevation to the top of the cliff is 63°.
a. How far away is the person from the base of the cliff?
b. What is the building’s height?
Answers
The distance from the person to the base of the cliff is 269.78 meters.
The height of the building from the base of the cliff is 829.37 meters
The situation forms right angle triangle.
The building is constructed on top the cliff that is 300 meters high.
Right angle triangle:Right angle triangle has one of its sides as 90 degrees. Therefore, the sides can be found using trigonometric ratios.
The height of the building from the cliff is 300m. let's find the hypotenuse side of the angle of elevation formed to the cliff.
Using sin rule,
300 / sin (72 - 63) = y / sin (180 - 162)
300 / sin 9 = y / sin 18
300 sin 18 = y sin 9
y = 300 sin 18 / sin 9
y = 92.7050983125 / 0.156
y = 594.230769231
Therefore, how far the person to the base of the cliff can be calculated as follows;
cos 63 = adjacent / hypotenuse
cos 63 = x / 594.2307
x = 594.2307 cos 63
x = 269.775092454
x = 269.78 meters
Therefore, the distance from the person to the base of the cliff is 269.78 meters.
height of the cliff / 269.78 = tan 63
height of cliff = 269.78 tan 63
height of cliff = 529.37493165
height of cliff = 529.37
The height of the building = 300 + 529.37 = 829.37493165 = 829.37 meters
learn more on right triangle here: https://brainly.com/question/14806301
5 added to the product of 12 and x is written as
Answers
The expression "5 added to the product of 12 and x" can be written as 12x + 5.
The expression "5 added to the product of 12 and x" can be written as:
12x + 5
Here's how we got this answer:
The product of 12 and x is written as 12x.
"5 added to the product of 12 and x" means we need to add 5 to 12x.
Putting these two parts together, we get the expression 12x + 5, which is the final answer.
Therefore, the expression "5 added to the product of 12 and x" can be written as 12x + 5. This is the algebraic representation of the given phrase.
Learn more about expressions:https://brainly.com/question/1859113
#SPJ11
The graduated cylinder contains 65 ml of water. The water level raises to 125 ml after the rock was added. What is the volume of the rock?
Answers
Solution: 60 ml
$ | The volume of the rock is calculated by subtracting the final volume from the initial volume. In this case, 125ml - 65ml = 60ml.
jackson bikes 2 miles in 15 mins at that rate how many miles will a bike in 45 mins
Answers
Let's use Cross-multiplication:
2mi ------------------------>15min
x mi------------------------->45min
So:
2/x = 15/45
Solving for x:
Multiply both sides by x:
x*(2/x) = x* 15/45
2 = 15x/45
Multiply both sides by 45:
45*2 = 45*(15x/45)
90 = 15x
Divide both sides by 15:
90/15 = 15x/15
6 = x
x = 6mi
Blaine is going bowling and will need to
pay $4 for shoes and then $3 for every
game. Write an equation for the
situation, if Blaine spends 16 dollars.
Answers
Answer: $16 = 4s + 3g
Step-by-step explanation:
s = shoes
g = games
Please help me !! I need help ASAP

Answers
Answer:
1/5
Step-by-step explanation:
.find all lower triangular 3×3 matrices x such that x3 is the zero matrix.
Answers
The lower triangular 3×3 matrices x such that x³ is the zero matrix have the form : x = [0 0 0,g h 0,0 0 0] where g and h any real number.
To find all lower triangular 3×3 matrices x such that x³ is the zero matrix, set up the equation x³ = 0 and solve for the elements of x. Let's represent a generic lower triangular matrix as:
x = [a b 0
d e f
g h i]
Multiplying x by itself three times,
x³ = [a b 0] × [a b 0] × [a b 0]
= [a²+bd ab 0]
[ad+be ae+bf b²]
[ag+bh ah+bh 0]
Setting this result equal to the zero matrix, we have:
a²+bd = 0
ab = 0
ad+be = 0
ae+bf = 0
b² = 0
ag+bh = 0
ah+bh = 0
0 = 0
0 = 0
0 = 0
From the equations above, deduce the following conditions for the elements of x:
a = 0
b = 0
d = 0
e = 0
f = 0
g can be any real number
h can be any real number
i = 0
To know more about triangular here
https://brainly.com/question/30950670
#SPJ4
mutiply (x-3)(4x+2) using the foul method
Answers
Answer: \(4x^2-10x-6\)
Step-by-step explanation:
\((x-3)(4x+2)\)
\(Expand\) \(the\) \(polynomial\) \(using\) \(the\) \(FOIL\) \(method\).
Therefore your answer is \(4x^2-10x-6\)
Answer:
4x^2 -10x + 6
Step-by-step explanation:
multiply (x-3)(4x+2) using the foil method
(x*4x)+(x*2)+(-3*4x)+(3*2)= 4x^2+2x-12x+6 = 4x^2 -10x + 6

What critical value of " should be used for a 95% confidence interval for the population mean based on a random sample of 30 observations? Find the t-table here. 1* = 2.042 * = 2.045 " = 2.147 * = 2.150
Answers
The critical value (t₍₃₀,₀.₀₅₎) for a 95% confidence interval, based on a random sample of 30 observations, is t₍₃₀,₀.₀₅₎ = 2.042.
Find the critical value?To determine the critical value, we refer to the t-table with degrees of freedom (df) equal to n - 1, where n represents the sample size. In this case, the sample size is 30, so the degrees of freedom is 30 - 1 = 29.
For a 95% confidence interval, we need to consider the two-tailed critical region. Since the area in each tail is 0.025 (0.05/2), we look for the corresponding value in the t-table at a significance level of α/2 = 0.025 for df = 29.
The closest value to 0.025 in the table is 2.042.
Therefore, the critical value (t₍₃₀,₀.₀₅₎) for a 95% confidence interval based on a random sample of 30 observations is t₍₃₀,₀.₀₅₎ = 2.042.
To know more about critical value, refer here:
https://brainly.com/question/32389590#
#SPJ4
Given the side measurements, classify the triangle as acute, right, obtuse, or not a triangle. 11, 13, 25 acute right obtuse not a triangle
Answers
RESPUESTA: no es un triangulo
EXPRICACION
The sum of any two sides must be greater than the other to be it triangle thus it will not be a triangle so option (D) is correct.
What is a triangle?A triangle is a 3-sided shape that is occasionally referred to as a triangle. There are three sides and three angles in every triangle, some of which may be the same.
The sum of all three angles inside a triangle will be 180°.
For any triangle, the sum of any two sides must be greater than the then third side.
As per the given sides, 11, 13, 25
11 + 13 < 25
24 < 25 so it will not a triangle.
Hence "The sum of any two sides must be greater than the other to be it triangle thus it will not be a triangle".
For more about triangles,
https://brainly.com/question/2773823
#SPJ2
the question is in the attached file

Answers
Answer:
D. 3.2553
Step-by-step explanation:
3/3.65 + 2/0.822
0.8219 + 2.4330
3.2553
Answer:
\(\sf D) \quad 3.2553\)
Step-by-step explanation:
Simplify the given expression:
\(\sf \dfrac{3}{\sqrt{5}+\sqrt{2}}+\dfrac{2}{\sqrt{5}-\sqrt{2}}\)
\(\sf = \dfrac{3(\sqrt{5}-\sqrt{2})}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}+\dfrac{2(\sqrt{5}+\sqrt{2})}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}\)
\(\sf = \dfrac{3(\sqrt{5}-\sqrt{2})}{3}+\dfrac{2(\sqrt{5}+\sqrt{2})}{3}\)
\(\sf = \dfrac{3\sqrt{5}-3\sqrt{2}+2\sqrt{5}+2\sqrt{2}}{3}\)
\(\sf =\dfrac{5\sqrt{5}-\sqrt{2}}{3}\)
Given:
\(\sf \sqrt{5} = 2.236\)\(\sf \sqrt{2} = 1.414\)Substitute the given values into the simplified expression:
\(\sf =\dfrac{5(2.236)-1.414}{3}\)
\(\sf =\dfrac{11.18-1.414}{3}\)
\(\sf =\dfrac{9.766}{3}\)
\(\sf =3.2553\:\:(4\:d.p.)\)
In order to prove the triangles pictured below as congruent BY SAS, we would need to know ___
a. AB≅AD
b. angle BAC≅angle DAC
c. angle ABC≅angle ADC
d. angle BCA≅angle DCA

Answers
Answer: D
Step-by-step explanation: i got it right
easy! what is the area of the circle

Answers
Answer:
#2
Step-by-step explanation:
Find the complement of the set given that u = {0, 1, 2, 3, 4, 5, 6, 7, 8}. (enter your answers as a comma-separated list.) the set of odd natural numbers less than 8
Answers
{ 0,2,4,6,8} is the complement of the set.
What is natural number in math?
Normative Numbers The numbers we use to count or place things in order are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. Complete numbers the range of numbers that includes zero and natural numbers.Is zero a natural number?
0 is not a natural number, so no. As we all know, natural numbers are positive integers with a range of 1 to infinity. However, we get a number when we combine 0 with a positive integer like 10, 20, or another number.u = {0, 1, 2, 3, 4, 5, 6, 7, 8}
Odd number less than 8 = { 1,3,5,7 }
complement = {0, 1, 2, 3, 4, 5, 6, 7, 8} - { 1,3,5,7 }
= { 0,2,4,6,8}
Learn more about natural number
brainly.com/question/17429689
#SPJ4
Find a unit vector u u in R 2 R2 such that u u is perpendicular to v . v. How many such vectors are there
Answers
Answer: hello some part of your question is missing
Let v=〈−2,5〉 in R^2,and let y=〈0,3,−2〉 in R^3.
Find a unit vector u in R^2 such that u is perpendicular to v. How many such vectors are there?
answer:
One(1) unit vector ( < 5/√29, 2 /√29 > ) perpendicular to 〈−2,5〉
Step-by-step explanation:
let
u = < x , y > ∈/R^2 be perpendicular to v = < -2, 5 > ------ ( 1 )
hence :
-2x + 5y = 0
-2x = -5y
x = 5/2 y
back to equation 1
u = < 5/2y, y >
∴ || u || = y/2 √29
∧
u = < 5 /2 y * 2 / y√29 , y*2 / y√29 >
= < 5/√29, 2 /√29 > ( unit vector perpendicular to < -2, 5 > )
Puzzle in the picture. the answer should be 23, explain how you did it

Answers
Step-by-step explanation:
try this option, all the details are in the attachment.
Note, the nine numbers. used in the solution are: 1, 2, 3, 4, 5, 6, 7, 8 and 9.

What are the main parts of writing a proof?
Answers
evaluate tan 60/ cos 45
Answers
Answer:
0.60922709536
Step-by-step explanation:
not sure if this is what you are looking for????
√6
im putting yall on folks
What is a formula for the nth term of the given sequence? 54, -36, 24...
Answers
Answer :
an = a1 + (n-1) d
an = 54 + (9-1) -90
an = 54 + (8) - 90
an = 54 - 720
an = - 666
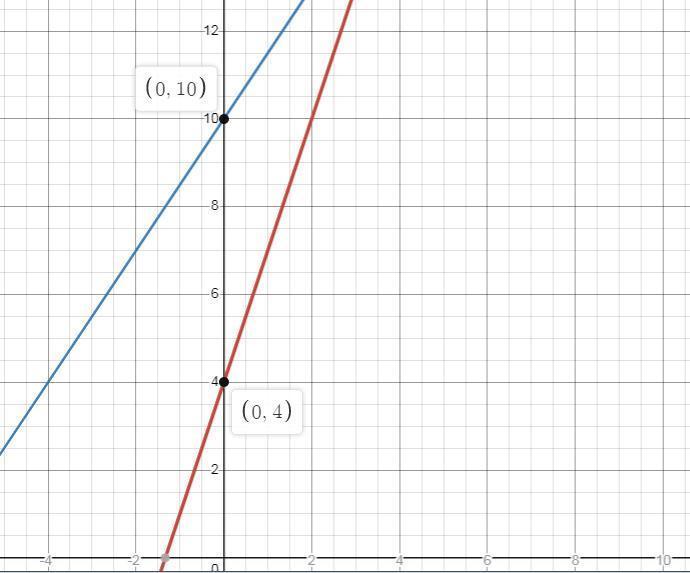
Christian is deciding between two parking garages. Garage A charges an initial fee of $4 to park plus $3 per hour. Garage B charges an initial fee of $10 to park plus $1.50 per hour. Let A represent the amount Garage A would charge if Christian parks for t hours, and let B represent the amount Garage B would charge if Christian parks for t hours. Graph each function and determine which garage would be cheaper if Christian needs to park for 2 hours.

Answers
If Christian needs to park for 2 hours, Garage A would be cheaper. And the graph is given below.
Comparing the charges:To compare the costs, we need to create mathematical functions that represent the total cost of each option based on the amount of time parked.
We can then graph these functions to visualize how they change as time increases, and we can use algebraic techniques such as substitution and simplification to determine which option is cheaper for a specific amount of time.
Here we have
Garage A charges an initial fee of $4 to park plus $3 per hour.
The amount charged by Garage A for t hours => 4 + 3t
Garage B charges an initial fee of $10 to park plus $1.50 per hour.
The amount charged by Garage B for t hours => 10 + 1.5t
After 2 hours the charges will be
Garage A, => 4 + 3(2) = 4 + 6 = $ 10
Garage B, => 10 + 1.5(2) = 10 + 3 = $ 13
Therefore,
If Christian needs to park for 2 hours, Garage A would be cheaper.
To graph, the lines make the values table as follows
For Garage A:
When t = 0, A = 4
When t=1, A = 7
When t=2, A = 10
Hence, the coordinate points are (0, 4) (1, 7), and (2, 10)
For Garage B:
When t=0, B = 10
When t=1, B = 11.5
When t=2, B = 13
Hence, the coordinate points are (0, 10) (1, 11.5), and (2, 13)
Hence, the graphs can be polt as shown below
Therefore,
If Christian needs to park for 2 hours, Garage A would be cheaper. And the graph is given below.
Learn more about Graphs at
https://brainly.com/question/29622081
#SPJ1

If Christian needs to park for 2 hours, Garage A would be cheaper. And the graph is given below.
What is a graph?
In computer science and mathematics, a graph is a collection of vertices (also known as nodes or points) connected by edges (also known as links or lines). Graphs are often used to represent relationships between objects or to model complex systems.
Here we have
Garage A charges an initial fee of $4 to park plus $3 per hour.
The amount charged by Garage A for t hours => 4 + 3t
Garage B charges an initial fee of $10 to park plus $1.50 per hour.
The amount charged by Garage B for t hours => 10 + 1.5t
After 2 hours the charges will be
Garage A, => 4 + 3(2) = 4 + 6 = $ 10
Garage B, => 10 + 1.5(2) = 10 + 3 = $ 13
Therefore,
If Christian needs to park for 2 hours, Garage A would be cheaper.
To graph, the lines make the values table as follows
For Garage A:
When t = 0, A = 4
When t=1, A = 7
When t=2, A = 10
Hence, the coordinate points are (0, 4) (1, 7), and (2, 10)
For Garage B:
When t=0, B = 10
When t=1, B = 11.5
When t=2, B = 13
Hence, the coordinate points are (0, 10) (1, 11.5), and (2, 13)
Hence, the graphs can be polt as shown below
Therefore, if Christian needs to park for 2 hours, Garage A would be cheaper. And the graph is given below.
Learn more about Graphs from the given link:
brainly.com/question/29622081
#SPJ1
Which is not a power function?.
Answers
A function containing a variable base raised to a fixed power is considered to be a power function.
when a function has a constant base raised to a variable power. This can be called an exponential function, not a power function A power function may be a function with a single term that is the product of a real number, a coefficient, and a variable raised to a fixed real number. It is in the form of f(x)=kx^p, where k and p are the real numbers whereas k is the coefficient.
to know more about the power function refer to the link https://brainly.com/question/24364138?referrer=searchResults.
#SPJ4
Is square root of 4 a polynomial?
Answers
Square root of 4 is not a polynomial. It is a quadratic function. Functions containing other operations like square root is not a polynomial.
A polynomial need not have any square root. polynomial is a finite sequence form. it must contain no square roots of variables, no fractional or negative powers on the variables, and no variables in the denominators of any fractions. Polynomial are sums and differences of polynomial terms. For an expression to be a polynomial term, any variables in the expression must have whole number powers. It should not have any square root, cube root or any negative values. Quadratic function can have square root cube roots and fraction values.
To learn more about Polynomial please visit:
https://brainly.com/question/15702527
#SPJ4
A joirney takes 1 hour and 30 minutes. Half the distance is travelled at an average apeed of 90km/h, while the ramaining distance is covered at an average speed of 100km/h. how long is the journey to the nearrst killometre?
Answers
Answer:
According to, the average speed formula is:
Average Speed = Total Distance / Total Time
Let x be the distance travelled at 90 km/h and y be the distance travelled at 100 km/h. Then we have:
x + y = Total Distance
x / 90 + y / 100 = 1.5 (Total Time in hours)
Solving for x and y, we get:
x = 60 km
y = 75 km
Therefore, the total distance is x + y = 135 km.
The average speed is then:
Average Speed = Total Distance / Total Time
= 135 / 1.5
= 90 km/h
Two sides of a triangle each measure 8 inches.
Maria says the triangle must be isosceles. Is Maria correct? Explain.
A.
No; the third side could measure 9 inches or 7 inches, and the triangle would be scalene.
B.
Yes; an isosceles triangle has at least two sides that have equal measures.
C.
Yes; the third side could measure 9 inches, and the triangle would be equilateral.
D.
No; the third side of the triangle could be 8 inches, and the triangle would be acute.
Answers
Answer:
B.) An isosceles triangle has at least two sides with equal measures.
Step-by-step explanation:
There are two equal sides and two equal angles in an isosceles triangle. There should be at least 2 equal sides for an Isosceles triangle. This means, even an equilateral triangle is an Isosceles triangle. In this case, at least two equal sides are 8 inches each. This is why the correct answer is 'Yes; an isosceles triangle has at least two sides that have equal measures.'
The figure shows a swing blown to one side by a
breeze. As long as the seat of the swing is parallel to
the top bar, the swing makes a parallelogram. In
ABCD, DC = 2 ft, BE 41/2 ft, and m<BAD = 75°

Answers
Answer:
AB=2 ft
ED=4.5 ft
BD=9 ft
m∠ABC=105°
m∠BCD=105°
m∠ADC=75°
Step-by-step explanation:
Factor out the greatest common factor. If the greatest common factor is 1, just retype the polynomial.
Answers
Using the definition of divisibility, 2p is the greatest common factor.
In the given question we have to factor out the greatest common factor. If the greatest common factor is 1, just retype the polynomial.
The given polynomial is 2p^3+6p.
Now taking 2p common from both terms
=2(p^2+3)
By the definition of divisibility, we get
2p | 2p^3 and 2p|6p, 2| 2p^3 and 2|6p also p|2p^3 and p|6p.
So, 2,p and 2p are common factors of 2p^3 and 6p.
Hence, 2p is the greatest common factor.
To learn more about definition of divisibility link is here
brainly.com/question/14316622
#SPJ4
The right answer is:
Factor out the greatest common factor. If the greatest common factor is 1, just retype the polynomial.
2p^3+6p
Find the expected value of the winnings
from a game that has the following payout
probability distribution:
Payout ($) 2 4 6 8 10
Probability 0.64 0.18 0.12 0.04 0.02
Expected Value = [?]
Round to the nearest hundredth.

Answers
The expected value of the winnings from this game is $3.24.
To find the expected value of the winnings, we multiply each payout by its corresponding probability and then sum up the results. Let's calculate it step by step:
Payout ($) Probability Payout x Probability
2 0.64 1.28
4 0.18 0.72
6 0.12 0.72
8 0.04 0.32
10 0.02 0.20
Now, let's sum up the values in the "Payout x Probability" column:
1.28 + 0.72 + 0.72 + 0.32 + 0.20 = 3.24
Therefore, the expected value of the winnings from this game is $3.24.
for such more question on expected value
https://brainly.com/question/15858152
#SPJ8