Write the equation of the sphere in standard form. x2 + y2 + z2 + 10x – 3y +62 + 46 = 0 Find its center and radius. center (x, y, z) = ( 1 y, ) radius Submit Answer
Answers
The center of the sphere is (-5, 3/2, -31), and its radius is \(\sqrt{(5675/4).\)
To write the equation of the sphere in standard form, we need to complete the square for the terms involving x, y, and z.
Given the equation \(x^2 + y^2 + z^2 + 10x - 3y + 62z + 46 = 0\), we can rewrite it as follows:
\((x^2 + 10x) + (y^2 - 3y) + (z^2 + 62z) = -46\)
To complete the square for x, we add \((10/2)^2 = 25\) to both sides:
\((x^2 + 10x + 25) + (y^2 - 3y) + (z^2 + 62z) = -46 + 25\\(x + 5)^2 + (y^2 - 3y) + (z^2 + 62z) = -21\)
To complete the square for y, we add \((-3/2)^2 = 9/4\) to both sides:
\((x + 5)^2 + (y^2 - 3y + 9/4) + (z^2 + 62z) = -21 + 9/4\\(x + 5)^2 + (y - 3/2)^2 + (z^2 + 62z) = -84/4 + 9/4\\(x + 5)^2 + (y - 3/2)^2 + (z^2 + 62z) = -75/4\)
To complete the square for z, we add \((62/2)^2 = 961\) to both sides:
\((x + 5)^2 + (y - 3/2)^2 + (z^2 + 62z + 961) = -75/4 + 961\\(x + 5)^2 + (y - 3/2)^2 + (z + 31)^2 = 3664/4 + 961\\(x + 5)^2 + (y - 3/2)^2 + (z + 31)^2 = 5675/4\)
Now we have the equation of the sphere in standard form:
\((x + 5)^2 + (y - 3/2)^2 + (z + 31)^2 = 5675/4.\)
The center of the sphere is given by the values inside the parentheses: (-5, 3/2, -31).
To find the radius, we take the square root of the right-hand side: sqrt(5675/4).
Therefore, the center of the sphere is (-5, 3/2, -31), and its radius is the square root of 5675/4.
To know more about sphere refer here:
https://brainly.com/question/30761440
#SPJ11
Related Questions
Find the best linear approximation, L(x), to f(x) = e' near x = 0. i.L(x) = x+1 ii. L(x) = x iii. LX) = c + 1
Answers
The best linear approximation to the function f(x) = e^x near x = 0 is L(x) = x + 1.
The given function is f(x) = e^x near x = 0.
To find the best linear approximation, L(x), we use the formula:
L(x) = f(a) + f'(a)(x-a),
where a is the point near which we are approximating.
Let a = 0, so that a is near the point x = 0.
f(a) = f(0) = e^0 = 1
f'(x) = d/dx (e^x) = e^x;
so f'(a) = f'(0) = e^0 = 1
Substituting these values into the formula: L(x) = 1 + 1(x-0) = x + 1
Therefore, the best linear approximation to f(x) = e^x near x = 0 is L(x) = x + 1.
For instance, linear approximation is used to approximate the change in a physical quantity due to a small change in another quantity that affects it.
To know more about linear approximation, visit:
https://brainly.com/question/1621850
#SPJ11
Pet Products Company uses an automated process to manufacture its pet replica products. For June the company had the following activities: Beginning work in process inventory 4,500 items,1/4 complete Units placed in production 15,000 units Units completed 17,500 units Ending work in process inventory 2.000 items.3/4 complete Cost of beginning work in process P5,250 Direct material costs, current P16,500 Conversion costs,current P23,945 The company uses FIFO Method Direct materials are placed into production at the beginning of the process and conversion costs are incurred evenly throughout the process. Required: 21.Calculate the Equivalent Units of Production-Conversion Cost.= 22.Calculate for the total material cost per unit = 23. Calculate for the total manufacturing cost per unit = 24.How much is the total cost for Started and Completed 25. How much is the total cost for Work in Process, Ending Inventory
Answers
The Equivalent Units of Production for conversion costs is 16,750 units. The total material cost per unit is P0.94. The total manufacturing cost per unit is P2.59. The total cost for Started and Completed is P47,680. The total cost for Work in Process, Ending Inventory is P5,180.
21. The Equivalent Units of Production-Conversion Cost = 16,750 units.
22. The total material cost per unit = P0.94.
23. The total manufacturing cost per unit = P2.59.
24. The total cost for Started and Completed = P47,680.
25. The total cost for Work in Process, Ending Inventory = P5,180.
To calculate the required values, we'll use the FIFO method.
21. Equivalent Units of Production-Conversion Cost:
Equivalent Units of Production = Units completed + (Ending work in process inventory * Degree of completion)
Equivalent Units of Production = 17,500 + (2,000 * 3/4)
Equivalent Units of Production = 17,500 + 1,500
Equivalent Units of Production = 19,000 units
22. Total Material Cost per Unit:
Total Material Cost per Unit = Total material costs / Equivalent Units of Production
Total Material Cost per Unit = P16,500 / 17,500
Total Material Cost per Unit = P0.94
23. Total Manufacturing Cost per Unit:
Total Manufacturing Cost per Unit = (Total material costs + Conversion costs) / Equivalent Units of Production
Total Manufacturing Cost per Unit = (P16,500 + P23,945) / 17,500
Total Manufacturing Cost per Unit = P40,445 / 17,500
Total Manufacturing Cost per Unit = P2.59
24. Total Cost for Started and Completed:
Total Cost for Started and Completed = Units completed * Total Manufacturing Cost per Unit
Total Cost for Started and Completed = 17,500 * P2.59
Total Cost for Started and Completed = P45,325
25. Total Cost for Work in Process, Ending Inventory:
Total Cost for Work in Process, Ending Inventory = Ending work in process inventory * Total Manufacturing Cost per Unit
Total Cost for Work in Process, Ending Inventory = 2,000 * P2.59
Total Cost for Work in Process, Ending Inventory = P5,180
To know more about total cost, visit
https://brainly.com/question/29509552
#SPJ11
I NEED HELP ASAP
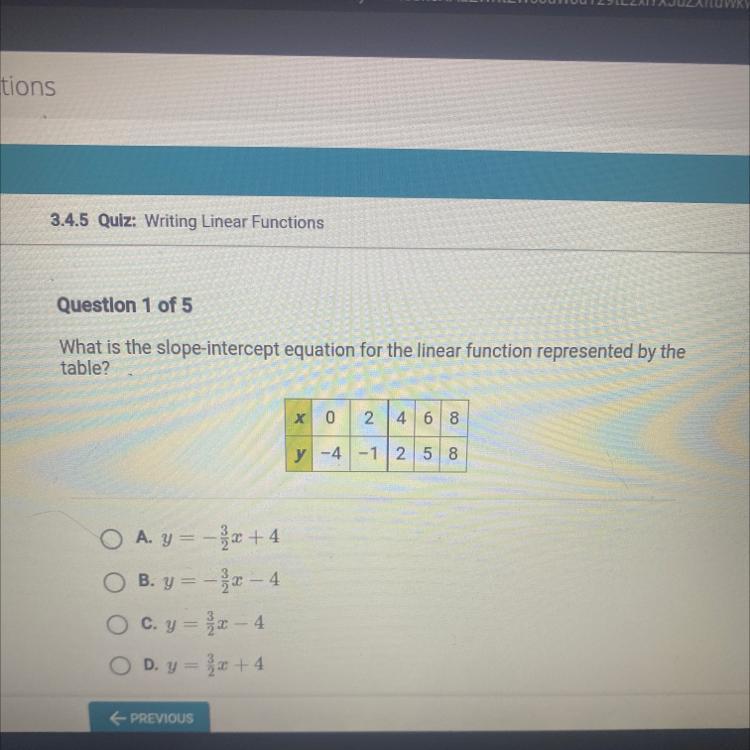
What is the slope-intercept equation for the linear function represented by the
table?
A. y = -x +4
B. y =
-x-4
C. y = x-4
OD. y=x+4
0
x
2 4 6 8
y -4 -1 258
Answers
Answer: C : y = 3/2 - 4
Step-by-step explanation:
Find the Slope (Slope Formula)
(4,2) (6,5)
m = (5-2)/(6-4)
m = 3/2
Find "b"
y = mx + b (Slope intercept form)
2 = 3/2(4) + b
2 = 6 + b
-4 = b
what values of m do line y=mx and curve y=x/(x^2 1) enclose a region? find area of the region
Answers
The area of region enclosed in line y=mx and curve y=x/(x^2 1) is \(ln(m \sqrt{(1/m^2 - 1))\)- m/2 (1/m^2 - 1) square unit.
The line y = mx intersects the curve y = x/(x^2 + 1) at two points, say (a, ma) and (b, mb), where a < b. Setting mx = x/(x^2 + 1), we can solve for x to get x = mx / (1 - m^2 x^2), or equivalently, (1 - m^2 x^2)x = mx, which gives x = 0 (when m = 0) or x^2 = 1/m^2 - 1, or equivalently, x = ±\(\sqrt{(1/m^2 - 1)\). Since the line is symmetric about the origin, we can assume m > 0.
For the line to enclose a region with the curve, we must have a < 0 < b, which means the intersection points are (- \(\sqrt{(1/m^2 - 1)\), - m \(\sqrt{(1/m^2 - 1)\)). and\(\sqrt{(1/m^2 - 1)\), m \(\sqrt{(1/m^2 - 1)\)). The area of the enclosed region is then:
∫_-\(\sqrt{(1/m^2-1)^\sqrt{(1/m^2-1)\)[x/(x^2+1) - mx] dx
We can use partial fraction decomposition to write x/(x^2+1) as 1/2 [1/(x-i) - 1/(x+i)], where i = sqrt(-1), and then integrate term by term to get:
∫_-\(\sqrt{(1/m^2-1)^\sqrt{(1/m^2-1)\) [x/(x^2+1) - mx] dx
= 1/2 [ln(x-i) - ln(x+i) - m/2 x^2] |_ - \(\sqrt{(1/m^2-1)^\sqrt{(1/m^2-1)\)
= ln(\(m \sqrt{(1/m^2 - 1))\) - m/2 (1/m^2 - 1)
Therefore, the area of the enclosed region is \(ln(m \sqrt{(1/m^2 - 1))\)- m/2 (1/m^2 - 1) square unit. This expression is undefined when m <= 1 or m >= -1, since in those cases, the curve and line do not intersect.
To know more about area of region:
https://brainly.com/question/28926053
#SPJ4
Work out the height of this triangle with base, b = 8.2mm and area, A = 227.14mm2.
Answers
Answer: the height of this triangle is 55.4 mm
Step-by-step explanation:
\(\displaystyle\\Area\ of\ a\ triangle:\ A =\ \frac{ah}{2} \\\\Hence,\\\)
Multiply both parts of the equation by 2:
\(2A=ah\)
Divide both parts of the equation by a:
\(\displaystyle\\\frac{2A}{a} =h\\\\Thus,\ h=\frac{2A}{a} \\\\h=\frac{2(227.14)}{8.2} \\\\h=\frac{454.28}{8,2} \\\\h=55.4\ mm\)
.3 times the value of 8/4 of positive a witch equals the sum of what
a =34.55
Answers
Answer:
I have difficulty understanding the question. I read it as "What is the value of a number that when multiplied by 0.3 times (8/4) is equal to 34.55. This doesn't seem correct, but if it is:
Step-by-step explanation:
(0.3)*(8/4)x = 34.55
(8/4)x = 115.17
x = (4/8)*(115.17)
x = 57.58
21 is the correct answer.
Calculate the median of the data set below. {0.3, 1.5, 3.8, 2.6, 1.5, 9.1, 4.2, 3.8, 1.5, 2.9} A. 3.8 B. 3.35 C. 2.75 D. 2.5
Answers
Answer:
2.75
Step-by-step explanation:
0.3,1.5,1.5,1.5,2.6,2.9,3.8,3.8,4.2,9.1
(smaller to greater)
middle of this is 2.6 and 2.9
so, 2.6+2.9=5.5
now we divide it by 2
so, 5.5/2=2.75
The pH of lemon juice at 298 K is found to be 2. 32. What is the concentration of mc014-1. Jpg ions in the solution? Use StartBracket upper H subscript 3 upper O superscript plus EndBracket equals 10 superscript negative p H. 1. 05 times 10 to the negative 3 moles per liter. 4. 79 times 10 to the negative 3 moles per liter. 2. 09 times 10 squared moles per liter. 9. 55 times 10 squared moles per liter.
Answers
The concentration of ions in the solution of lemon juice whose pH value is 2.32 is 4.79×10⁻³ M.
What is pH value?The pH value shows that how much a solution is acidic or basic. The range of the pH value lies between the 0-14.
The pH value can be calculated with the following formula.
\(\rm pH=log[H^{+}]\)
Here, [H⁺] is the molar hydrogen ion concentration.
The pH of lemon juice at 298 K is found to be 2. 32. Put this value of pH in the above formula as,
\(\rm 2.32=log[H^{+}]\\\ [H^{+}]=4.79\times10^{-3} \rm \; M\)
Hence, the concentration of ions in the solution of lemon juice whose pH value is 2.32 is 4.79×10⁻³ M.
Learn more about the pH value here;
https://brainly.com/question/940314
Answer:
B ✔️
Step-by-step explanation:
May I please get help with all the questions

Answers
Answer:
1. g(3) = 1
2. (f + g)(2) = f(2) + g(2) = 2 + 3 = 5
3. f(g(4)) = 2
4. g(f(4)) = 1
5. f(f(4)) = 2
6. g(g(2)) = 1
7. base on the chart, the value 3 of g(x) can be gain only for x = 0
Help me please answer thanks

Answers
Answer:
I think it would be each girl scored 2 points, and each boy only scored one. :)
What is the asymptote of the graph shown?
y=

Answers
Answer:
to this question is it is 1.01
A survey was done that asked people to indicate whether they preferred to ride a
street bike or a mountain bike. The results of the survey are shown in the two-way
table.
Amjed is making a relative frequency table from this data.
What operation should Amjed perform to determine the relative frequency of a
person over 30 years old who prefers to ride a mountain bike? 1) Subtract 25 from 462, then divide by 462. 2) Divide 25 by 462. 3) Add 180 to 462, then divide by 463. 4) Divide 180 by 462

Answers
The operation that Amjed should perform to determine the relative frequency of a person over 30 years old who prefers to ride a mountain bike is given as follows:
2) Divide 25 by 462.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of people is given as follows:
58 + 164 + 215 + 25 = 462.
Out of these people, 25 prefer mountain bike, hence the relative frequency is given as follows:
25/462.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
: Prove that a) X'Y' + X'Y +XY = X' +Y b) A'BC' + ABC' + BC'D = BC' Find the complement of the following function a) WX(Y'Z+YZ') + W'X'(Y' +Z)(Y+Z') b) (A+B'+C') (A'B' +C)(A + B'C') Find Dual of question 2 (a, b),
Answers
a) X'Y' + X'Y + XY simplifies to X' + Y.
b) A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the functions:
a) Complement is W' + X' + YZ.
b) Complement is (A' + B + C)(A'B' + C' + A'B).
a) To prove X'Y' + X'Y + XY = X' + Y, we can use Boolean algebra identities:
X'Y' + X'Y + XY
= Y'(X' + X) + XY(Distributive Law)
= Y' + XY(X + X' = 1)
= X' + Y(Commutative Law)
Therefore, X'Y' + X'Y + XY simplifies to X' + Y.
b) To prove A'BC' + ABC' + BC'D = BC', we can simplify the expression using Boolean algebra:
A'BC' + ABC' + BC'D
= BC'(A' + A) + BC'D (Distributive Law)
= BC' + BC'D(A + A' = 1)
= BC'(BC' + BC'D = BC' + BC'(1) = BC')
Hence, A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the given functions:
a) The complement of WX(Y'Z + YZ') + W'X'(Y' + Z)(Y + Z') is W' + X' + YZ.
b) The complement of (A + B' + C')(A'B' + C)(A + B'C') is (A' + B + C)(A'B' + C' + A'B).
Learn more About Distributive Law from the given link
https://brainly.com/question/25224410
#SPJ11
The width of a rectangle is 2 m. The length of the rectangle is 4 times a number increased by 4. If the area of the rectangle is 48, what is the length of the rectangle?
Answers
Answer:
8
Step-by-step explanation:
The length of the rectangle is 24 meter.
Here,
The width of a rectangle is 2 m.
The length of the rectangle is 4 times a number increased by 4.
The area of the rectangle is 48.
We have to find the length of a rectangle.
What is Area of rectangle?
The formula for the area of a rectangle is multiply length x width.
Now,
The width of a rectangle = 2 m
Let a number is x.
Then the length of rectangle =(4x + 4) m
Area of rectangle = length x width.
= (4x + 4) * 2
Here, The area of the rectangle is 48.
So,
(4x + 4) * 2 = 48
Divide both side by 2,
4x + 4 = 24
4x = 24 -4
4x = 20
Divide both side by 4,
x = 5
Hence, the length of rectangle,
⇒ 4x + 4 = 4 * 5 + 4 = 20 + 4 = 24 m
So, The length of the rectangle is 24 meter.
Learn more about the area of rectangle visit:
https://brainly.com/question/2607596
#SPJ2
Find the surface area of the composite figure. Round to the nearest tenth if necessary.

Answers
Answer:
Step-by-step explanation:
· Find the surface area of a cone with a slant height of 8 cm and a radius of 3 cm. SA = B + πrS = (πr2) + πrs = (π(32)) + π(3)(8) = 9π + 24π = 33πcm2 = 103.62cm2. Find the surface area of a rectangular pyramid with a slant height of 10 yards, a base width (b) of 8 yards and a base length (h) of 12 yards.
what does it mean if the first of a two step tuberculin skin test is negative and the second is positive? what does it mean if both tests are negative?
Answers
It reads the second test. o Negative - assume that the person is not infected. o If positive, take a prior TB infection into consideration. Any asymptomatic person whose chest X-ray shows no signs of an active illness will be forwarded to the health department.
What brings about TB infection?
The bacteria Mycobacterium tuberculosis is the one that causes tuberculosis (TB).
When someone who has active TB disease in their lungs coughs or sneezes and the TB bacteria-containing droplets are ejected, the disease is disseminated when the other person inhales them.
What transpires if you have TB?
Feelings of sickness or weakness, weight loss, a high temperature, and nocturnal sweats are some of the common signs of TB disease.
Coughing, chest pain, and the coughing up of blood are other signs of TB lung disease. Depending on the location affected, TB illness symptoms may manifest in various body parts.
Learn more about TB infection
brainly.com/question/13521671
#SPJ4
If K < 1 , Δ G is: a. zero b. negative c. one d. positive
Answers
If the equilibrium constant (K) < 1 , then, the Gibbs free energy change(ΔG) is positive. So, option D is correct alternative.
The relative concentrations of reactants and products in a chemical reaction are gauged by the equilibrium constant (K), which is the case in this case. Typical chemical reactions are as follows:
aA + bB ⇌ cC + dD
The equilibrium constant is defined as:
\(K = \frac{[C]^c[D]^d }{ [A]^a[B]^b}\)
Where [A], [B], [C], and [D] are the molar concentrations of reactants and products at equilibrium, and a, b, c, and d are the stoichiometric coefficients of the balanced chemical equation.
The Gibbs free energy change (ΔG) is a measure of the amount of energy available to do useful work during a chemical reaction.
The following equation describes the relationship between the equilibrium constant (K) and the change in the Gibbs free energy (ΔG):
ΔG = -RTln(K)
Where R is the gas constant and T is the temperature.
If K < 1, then ln(K) is negative. So, to make the right-hand side of the equation negative, ΔG must be positive.
To know extra about Gibbs free energy
brainly.com/question/13318988
#SPJ4
Which sequence of transformations would yield a trapezoid similar to the original trapezoid but not congruent?A)reflection and dilationB)reflection and rotationC)rotation and reflectionD)translation and rotation help please
Answers
The sequence of transformations will be relection and dilation. Then the correct option is A.
What is a transformation of geometry?A spatial transformation is each mapping of feature shapes to itself and it maintains some spatial correlation between figures.
The sequence of transformations would yield a trapezoid similar to the original trapezoid but not congruent.
Reflection does not change the size and shape of the geometry.
Rotation does not change the size and shape of the geometry.
Translation does not change the size and shape of the geometry.
Dilation does not change the shape but changes the size of the geometry.
Then the correct option is A.
More about the transformation of geometry link is given below.
https://brainly.com/question/22532832
#SPJ1
In triangle GHJ, mH = 85° and mG = 60°.
Choose the correct symbol to put in the blank.
HJ ___ JG
<
=
>
Answers
Answer: The correct symbol is '<'.
Step-by-step explanation:
Given: In triangle GHJ
\(m\angle H=85^{\circ}\) and \(m\angle G=60^{\circ}\)
Here angle H is opposite to side JG and angle G is opposite to side HJ
We know that,
The side opposite to the greater angle of a triangle is greater.
Since \(m\angle H> m\angle G\)
Then, JG > HJ
Hence, HJ < JG
A group of veterinarians at a major veterinary hospital was interested in investigating a possible link between enteroliths, stones that form in the colon of horses, and diet. They decided to conduct a survey of feeding practices of horses admitted to the veterinary hospital. To obtain a simple random sample they used a computer to generate four-digit ID numbers for all horses. They used random digit tables to select the horses. Which is a step in selecting a random sample by this procedure?
1. Pick a random starting point in the table and read four digits.
2. Read four digits across a line and, if the four digits correspond to a horse ID, select the animal.
3. Discard any sequence that does not correspond to a horse ID and move to the next four digits.
4. All of the answer choices are correct.
Answers
1. Pick a random starting point in the table and read four digits.
This is the step in selecting a random sample by this procedure
What is sample?
In statistics, a sample refers to a group of individuals, objects, or events that are selected from a larger population to represent that population. Sampling is the process of selecting a subset of individuals or items from a larger population in order to infer something about the whole population.
The step in selecting a random sample by the procedure described in the scenario is step 1: Pick a random starting point in the table and read four digits. This step ensures that the selection of horses is entirely random, with each horse having an equal chance of being chosen. By starting at a random point in the table and selecting the first four digits, the veterinarians are eliminating any possible bias in the selection process. The subsequent steps involve using the selected four digits to determine if they correspond to a horse ID, discarding any sequences that do not match, and repeating the process until the desired sample size is reached.
To learn more about sample visit:
https://brainly.com/question/27829028
#SPJ4
Jackson and Flora both have bank accounts, and they use credit cards.
Use the number line to determine if they can pay off the credit card bill.
A. Jackson has $20 in his account. He uses a credit card to spend $30 on a
coat and $10 on a movie. Jackson then deposits $50 into his account.
How much will Jackson have left after he pays the credit card bill?
Answers
To assess the accuracy of laboratory scale, a standard weight known to weigh 10 grams is weighed repeatedly. the weight is weighed 40 times. the mean result is 10.230 grams. the standard deviation of the scale readings is 0.020 gram. construct a 98% confidence interval for the mean of repeated measurements of the weight. what is the margin of error? round your answers to three decimal places.
Answers
To construct a 98% confidence interval for the mean of repeated measurements of the weight, we can use the formula:
Confidence interval = mean ± (t-value) x (standard error)
where the standard error is the standard deviation of the sample divided by the square root of the sample size, and the t-value is based on the degrees of freedom (n-1) and the desired level of confidence. Since we are given the sample mean, standard deviation, and sample size, we can plug in the values and solve for the confidence interval and margin of error.
First, we need to calculate the standard error:
Standard error = standard deviation / √n
Standard error = 0.020 gram / √40
Standard error = 0.00316 gram
Next, we need to find the t-value for a 98% confidence interval with 39 degrees of freedom. We can use a t-distribution table or calculator to find the t-value, which is approximately 2.423.
Substituting the values into the formula, we get:
Confidence interval = 10.230 ± (2.423)(0.00316)
Confidence interval = 10.230 ± 0.00766
Rounding to three decimal places, the 98% confidence interval for the mean weight is (10.222, 10.238) grams. The margin of error is half the width of the confidence interval, which is 0.00766/2 = 0.00383 grams
2. Given: 2(x– 9) = -10; Prove: X= 4
What are the reasons
Answers
Answer:
true
Step-by-step explanation:
If u put 4 into x's place in the equation it equals 10
2(4-9) =-10
2(-5) = -10
negative times a positive is always a negative
PEMDAS
quick!!!! i will mark brainliest who gets it right first

Answers
Answer: um a= c+ 6
Step-by-step explanation:
6. Find the average of the middle 80% of the
following series: 3,7, 39, 41, 57, 84, 91, 95, 110,
144
070.5
067.1
O52.5
057
O 65.5
Answers
following series: 3,7, 39, 41, 57, 84, 91, 95, 110,
144
070.5
067.1
O52.5
057
O 65.5
The average of the middle 80% of the series is option (E) 65.5 is the correct answer.
What is an average?Average is the mean of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
For the given situation,
The series of numbers are 3,7, 39, 41, 57, 84, 91, 95, 110, 144.
The middle 80% of the numbers are 7, 39, 41, 57, 84, 91, 95, 110.
The formula of average of numbers is
\(Average = \frac{Sum of all numbers}{Total number of numbers}\)
⇒ \(Average = \frac{7+39+41+57+84+91+95+110}{8}\)
⇒ \(Average = \frac{524}{8}\)
⇒ \(Average = 65.5\)
Hence we can conclude that the average of the middle 80% of the series is option (E) 65.5 is the correct answer.
Learn more about the average here
https://brainly.com/question/24130817
#SPJ2
Styrofoam for facde insulation should be 0.6 cm think. 2% error is allowed. what is the smallest allowable thinkness of the styrofoam?
Answers
The smallest allowable thickness of the Styrofoam would be 0.98 times the desired thickness.
To find the smallest allowable thickness of the Styrofoam for facade insulation, we need to consider the 2% error allowed.
Let's assume the desired thickness is represented by x.
Since the error allowed is 2%, we can calculate the maximum acceptable error as (2/100) * x.
To find the smallest allowable thickness, we subtract the maximum acceptable error from the desired thickness: x - (2/100) * x.
Simplifying this expression, we get x(1 - 2/100) or x * 0.98.
Therefore, the smallest allowable thickness of the Styrofoam would be 0.98 times the desired thickness.
Know more about error here:
https://brainly.com/question/28008941
#SPJ11
5k(k-9)=0 solve for k
Answers
Step-by-step explanation:
5k²-45= 0
5k²= 0 +45
k²= 45/5
k²= 9
or
k = 9/2 = 4.5
Find the volume of the solid enclosed by the paraboloid z = 2 + x2 + (y - 2)2 and the planes z = 1, x = ?2, x = 2, y = 0, and y = 3.
Answers
Main Answer:The volume of the solid enclosed by the paraboloid and the planes is 18.67 cubic units.
Supporting Question and Answer:
How do we calculate the volume of a solid bounded by surfaces using triple integration?
To calculate the volume of a solid bounded by surfaces using triple integration, we set up a triple integral with the integrand equal to 1, representing the infinitesimal volume element. The bounds of integration are determined by the equations defining the surfaces that enclose the solid. By evaluating the triple integral over the specified region, we can find the volume of the solid.
Body of the Solution: To find the volume of the solid enclosed by the paraboloid z = 2 + x^2 + (y - 2)^2 and the planes z = 1, x = -2, x = 2, y = 0, and y = 3, we can set up a triple integral in the given region.
To find the volume,using the triple integral:
V = ∫∫∫ R (1) dz dy dx
where R is the region bounded by the given planes and the paraboloid.
The bounds of integration for x are -2 to 2, for y are 0 to 3, and for z are the lower bound function z = 1 and the upper bound function z = 2 + x^2 + (y - 2)^2.
Setting up the triple integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 ∫ from z = 1 to 2 + x^2 + (y - 2)^2 (1) dz dy dx
Integrating the innermost integral with respect to z:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [(2 + x^2 + (y - 2)^2) - 1] dy dx
Simplifying the expression inside the integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [x^2 + (y - 2)^2 + 1] dy dx
Integrating the inner integral with respect to y:
V = ∫ from x = -2 to 2 [x^2(y) + ((y - 2)^3)/3 + y] evaluated from y = 0 to 3 dx
Substituting the limits of integration for y:
V = ∫ from x = -2 to 2 [x^2(3) + (3 - 2)^3/3 + 3 - (x^2(0) + (0 - 2)^3/3 + 0)] dx
Simplifying further:
V = ∫ from x = -2 to 2 [3x^2 +2/3] dx
Integrating the final integral with respect to x:
V = [(x^3) + (2/3)x] evaluated from x = -2 to 2
Evaluating the expression at the limits:
V = [(2^3) +(2/3) 2] - [((-2)^3) + (2/3)(-2)]
V = (8 +4/3) - (-8 - 4/3)
V = 16+8/3
V =56/3
Final Answer:Therefore, the volume of the solid enclosed by the paraboloid and the given planes is 56/3 cubic units.
To learn more about the volume of a solid bounded by surfaces using triple integration from the given link
https://brainly.com/question/31473156
#SPJ4
The volume of the solid enclosed by the paraboloid and the planes is 18.67 cubic units.
How do we calculate the volume of a solid bounded by surfaces using triple integration?To calculate the volume of a solid bounded by surfaces using triple integration, we set up a triple integral with the integrand equal to 1, representing the infinitesimal volume element. The bounds of integration are determined by the equations defining the surfaces that enclose the solid. By evaluating the triple integral over the specified region, we can find the volume of the solid.
Body of the Solution: To find the volume of the solid enclosed by the paraboloid z = 2 + x^2 + (y - 2)^2 and the planes z = 1, x = -2, x = 2, y = 0, and y = 3, we can set up a triple integral in the given region.
To find the volume,using the triple integral:
V = ∫∫∫ R (1) dz dy dx
where R is the region bounded by the given planes and the paraboloid.
The bounds of integration for x are -2 to 2, for y are 0 to 3, and for z are the lower bound function z = 1 and the upper bound function z = 2 + x^2 + (y - 2)^2.
Setting up the triple integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 ∫ from z = 1 to 2 + x^2 + (y - 2)^2 (1) dz dy dx
Integrating the innermost integral with respect to z:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [(2 + x^2 + (y - 2)^2) - 1] dy dx
Simplifying the expression inside the integral:
V = ∫ from x = -2 to 2 ∫ from y = 0 to 3 [x^2 + (y - 2)^2 + 1] dy dx
Integrating the inner integral with respect to y:
V = ∫ from x = -2 to 2 [x^2(y) + ((y - 2)^3)/3 + y] evaluated from y = 0 to 3 dx
Substituting the limits of integration for y:
V = ∫ from x = -2 to 2 [x^2(3) + (3 - 2)^3/3 + 3 - (x^2(0) + (0 - 2)^3/3 + 0)] dx
Simplifying further:
V = ∫ from x = -2 to 2 [3x^2 +2/3] dx
Integrating the final integral with respect to x:
V = [(x^3) + (2/3)x] evaluated from x = -2 to 2
Evaluating the expression at the limits:
V = [(2^3) +(2/3) 2] - [((-2)^3) + (2/3)(-2)]
V = (8 +4/3) - (-8 - 4/3)
V = 16+8/3
V =56/3
Therefore, the volume of the solid enclosed by the paraboloid and the given planes is 56/3 cubic units.
To learn more about the volume of a solid
brainly.com/question/31473156
#SPJ4
If 4000 dollars is invested in a bank account at an interest rate of 5 percent per year, Find the amount in the bank after 6 years if interest is compounded annually: (Round to the nearest penny.) Fin
Answers
the amount in the bank after 6 years, compounded annually, is approximately $5306.36.
oTo calculate the amount in the bank after 6 years with an interest rate of 5 percent per year, compounded annually, we can use the formula for compound interest:
A = P(1 + r/n)^(n*t)
Where:
A is the final amount
P is the principal amount (initial investment)
r is the interest rate (in decimal form)
n is the number of times interest is compounded per year
t is the number of years
In this case, P = $4000, r = 5% = 0.05, n = 1 (compounded annually), and t = 6.
A = 4000(1 + 0.05/1)^(1*6)
A = 4000(1.05)^6
A ≈ $5306.36
Therefore, the amount in the bank after 6 years, compounded annually, is approximately $5306.36.
To learn more about Bank click herehere:brainly.com/question/7275286
#SPJ11
2x + 3 +2x +3 hhhhhhh