Answers
Answer:
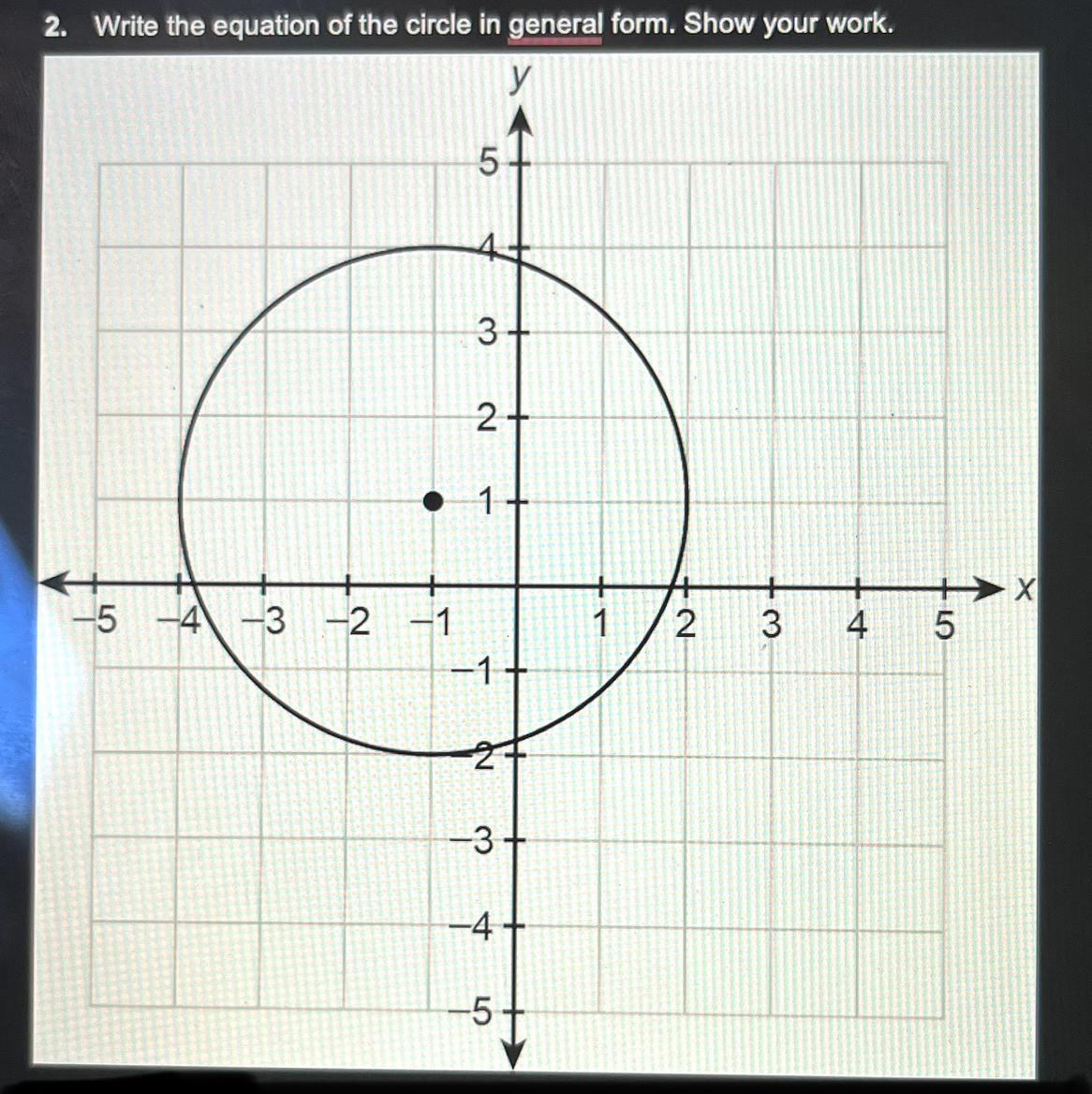
\( {(x + 1)}^{2} + {(y - 1)}^{2} = 9\)
Related Questions
0.127450980392 as fraction
Answers
\(\frac{1820728291}{14285714286}\)
Question 5: ( 10 +2 +4 +4 marks ) a. Consider the parabola f(x) = x2 - 4x +3
i) Write the equation in vertex form.
ii) Find the vertex and axis of symmetry. iii) Find the x-intercept and the y-intercept
b.write the quadratic functiion for the parabola that has vertex (-3,2) and passes through (1,4)
Answers
i) The equation in vertex form is f(x) = (x - 2)² - 1.
ii) The vertex of the parabola is (2, -1).
iii)The x-intercepts are (1, 0) and (3, 0) and the y-intercept is (0, 3).
b. The quadratic function is: f(x) = (1/8)(x + 3)² + 2.
Quadratic functions and parabolas:
A quadratic function is a function of form f(x) = ax² + bx + c, where a, b, and c are constants and a ≠ 0. The graph of a quadratic function is a U-shaped curve called a parabola.
The vertex of a parabola is the point where the parabola changes direction. It lies on the axis of symmetry, which is a vertical line that divides the parabola into two equal halves.
Here we have
The parabola f(x) = x² - 4x +3
a. Consider the parabola f(x) = x^2 - 4x + 3
i) To write the equation in vertex form, we complete the square:
f(x) = x² - 4x + 3
= (x² - 4x + 4) - 1
= (x - 2)² - 1
Therefore, the equation in vertex form is f(x) = (x - 2)² - 1.
ii) The vertex of the parabola is (2, -1). The axis of symmetry is the vertical line passing through the vertex, which is x = 2.
iii) To find the x-intercepts, we set f(x) = 0:
(x - 2)² - 1 = 0
(x - 2)² = 1
x - 2 = ±1
x = 1, 3
Therefore, the x-intercepts are (1, 0) and (3, 0).
To find the y-intercept, we set x = 0:
f(0) = 0² - 4(0) + 3 = 3
Therefore, the y-intercept is (0, 3).
b. To write the quadratic function for the parabola that has vertex (-3, 2) and passes through (1, 4), we use the vertex form of the quadratic equation:
f(x) = a(x - h)² + k,
where (h, k) is the vertex.
Substituting the given values, we get:
f(x) = a(x + 3)² + 2
To find the value of a, we substitute the point (1, 4) into the equation:
4 = a(1 + 3)² + 2
2 = 16a
a = 1/8
Therefore,
i) The equation in vertex form is f(x) = (x - 2)² - 1.
ii) The vertex of the parabola is (2, -1).
iii)The x-intercepts are (1, 0) and (3, 0) and the y-intercept is (0, 3).
b. The quadratic function is: f(x) = (1/8)(x + 3)² + 2.
Learn more about Parabolas at
https://brainly.com/question/31142122
#SPJ4
A.i. The equation in vertex form is f(x) = (x - 2)² - 1.
ii. The axis of symmetry is the vertical line passing through the vertex, which is x = 2.
iii. The x-intercepts are x = 1 and x = 3. The y-intercept is y = 3.
B. The quadratic function for the parabola is:
f(x) = (1/8)(x + 3)^2 + 2.
How did we arrive at these values?a.
i) To write the equation in vertex form, we need to complete the square. The general vertex form of a parabola is given by f(x) = a(x - h)² + k, where (h, k) represents the vertex.
Let's complete the square for the given parabola f(x) = x² - 4x + 3:
f(x) = x² - 4x + 3
= (x² - 4x + 4) - 4 + 3 [Adding and subtracting (4/2)² = 4 to complete the square]
= (x - 2)² - 1
So, the equation in vertex form is f(x) = (x - 2)² - 1.
ii) Comparing the equation f(x) = (x - 2)² - 1 with the vertex form f(x) = a(x - h)² + k, we can see that the vertex is (h, k) = (2, -1). The axis of symmetry is the vertical line passing through the vertex, which is x = 2.
iii) To find the x-intercepts, set f(x) = 0 and solve for x:
(x - 2)² - 1 = 0
(x - 2)² = 1
x - 2 = ±√1
x - 2 = ±1
x = 2 ± 1
So, the x-intercepts are x = 1 and x = 3.
To find the y-intercept, set x = 0 in the equation:
f(0) = (0 - 2)² - 1
= (-2)² - 1
= 4 - 1
= 3
So, the y-intercept is y = 3.
b.
To write the quadratic function for the parabola with a vertex at (-3, 2) and passing through (1, 4), use the vertex form of a parabola.
The vertex form of a parabola is f(x) = a(x - h)² + k, where (h, k) represents the vertex.
Using the given vertex (-3, 2):
h = -3 and k = 2.
Substituting the values of h and k:
f(x) = a(x - (-3))² + 2
= a(x + 3)² + 2
Now, use the point (1, 4) to find the value of 'a'.
Substituting x = 1 and f(x) = 4 in the equation:
4 = a(1 + 3)² + 2
4 = a(4²) + 2
4 = 16a + 2
16a = 4 - 2
16a = 2
a = 2/16
a = 1/8
Therefore, the quadratic function for the parabola is: f(x) = (1/8)(x + 3)² + 2.
learn more about quadratic function: https://brainly.com/question/1214333
#SPJ4
a jar contains 2 red marbles and 5 green marbles. players 1 and 2 take turns drawing marbles from the jar, with player 1 going first. after a marble is drawn, it is not replaced. whoever selects a red marble first wins the game. what is the chance that player 1 wins?
Answers
The chance that Player 1 wins is 11/21, or approximately 0.524 or 52.4%.
To calculate the probability that Player 1 wins, we can consider the possible outcomes of the game.
Player 1 can win in two ways:
Player 1 draws a red marble on their first turn.
Player 1 and Player 2 both draw green marbles on their first turns, and then Player 1 draws a red marble on their second turn.
Let's calculate the probability of each scenario:
Probability of Player 1 drawing a red marble on the first turn:
Player 1 has 2 red marbles out of a total of 7 marbles (2 red + 5 green) initially in the jar. So the probability is 2/7.
Probability of both players drawing green marbles on their first turns, and Player 1 drawing a red marble on their second turn:
After Player 1's first turn, there are 6 marbles left in the jar (2 red + 4 green). The probability of Player 1 drawing a red marble on their second turn is 2/6.
To calculate the overall probability of Player 1 winning, we add the probabilities of the two scenarios:
P(Player 1 wins) = P(Player 1 draws a red marble on the first turn) + P(both draw green, and Player 1 draws red on second turn)
= 2/7 + (5/7) * (2/6)
= 2/7 + 10/42
= 2/7 + 5/21
= (6 + 5)/21
= 11/21
Therefore, the chance that Player 1 wins is 11/21, or approximately 0.524 or 52.4%.
To learn more about probability visit;
https://brainly.com/question/31828911
#SPJ11
Do number 13 please

Answers
Explanation: since each rod is 3.75 inches, we can divide 20, our total length, by 3.75, and we get 5.33. That means we can make five full rods, and we have a third of a rod left over. 3.75/3 gets us 1.25, so we know that is our remainder of metal left over.
Marcy’s breakfast table has a square table top with an area of 36 square feet. What is the approximate diagonal length of the table top? Round to the nearest tenth.
Answers
Answer:
8.5 ft = length of diagonal
Step-by-step explanation:
If A = 36 ft^2, then s (length of one side) = 6 ft.
The diagonal and any one side create a 45 degree angle.
sin 45 degrees = (length of side opposite the 45 degree angle)/hypotenuse
6 ft 6√2 ft
Then (length of hypotenuse) = ------------------ = ---------------
sin 45 deg 1
This works out to 8.5 ft = length of diagonal
is the point below which a specified percentage of the observations fall.
Answers
In mathematics, the point below which a specified percentage of the observations fall is commonly referred to as the percentile.
A percentile is a measure that indicates the relative position of a particular value within a dataset.
For example, if a value is at the 80th percentile, it means that 80% of the observations in the dataset are below that value, and only 20% of the observations are above it.
Percentiles are often used to analyze and understand the distribution of data, especially in fields such as statistics, probability, and data analysis. They provide insights into how individual data points compare to the overall dataset and help identify outliers or extreme values.
A percentile is a statistical measure that indicates the relative standing of a particular value within a dataset. It represents the point below which a specified percentage of the observations or data points fall. Percentiles are primarily used to understand the distribution of data and analyze how individual values compare to the overall dataset.
To calculate a percentile, the dataset is arranged in ascending order, from the smallest value to the largest value. The position of a specific percentile is then determined based on the percentage of data points below it. For example, the 75th percentile represents the value below which 75% of the data points fall.
Percentiles are commonly used in various fields, including statistics, probability, and data analysis. They provide valuable insights into the spread, variability, and distribution of data. Here are a few key points to consider:
1. Median: The median is the 50th percentile, representing the value that divides the dataset into two equal halves. It is a measure of central tendency and provides information about the middle point of the distribution.
2. Quartiles: Quartiles divide the dataset into four equal parts. The first quartile, or the 25th percentile (Q1), represents the value below which 25% of the data points fall. The third quartile, or the 75th percentile (Q3), represents the value below which 75% of the data points fall. The difference between Q3 and Q1 is known as the interquartile range (IQR) and provides insights into the spread of the middle 50% of the data.
3. Percentile Ranks: Percentile ranks indicate the percentage of data points that are below a specific value. For example, if a student scores in the 80th percentile on a standardized test, it means they performed better than 80% of the test-takers.
4. Outliers: Percentiles can be useful in identifying outliers, which are data points that significantly deviate from the rest of the dataset. Extremely high or low percentiles may indicate unusual or extreme values that warrant further investigation.
5. Normal Distribution: In a normal distribution, the 50th percentile (median) coincides with the mean and mode, and specific percentiles have known standard deviations from the mean (e.g., the 68-95-99.7 rule).
Percentiles are versatile tools for summarizing and analyzing data, providing valuable insights into the distribution and relative positions of individual values. They enable comparisons and help make informed decisions based on the characteristics of a dataset.
to more about Median visit:
brainly.com/question/1153198
#SPJ11
A farmer had a total of 995 horses and cows. After selling some of the horses and cows, he had 510 horses and 390 cows left. How many horses and cows did he sell altogether?
a =
horses and cows
Answers
NEED ANSWER ASAP!!! WILL GIVE BRAINLIEST TO WHO ANSWERS FIRST!
Solve for x: 2x − 2 > 4x + 6. (5 points)
x −4
x 4
Answers
Answer:
x < - 4
Step-by-step explanation:
Given
2x - 2 > 4x + 6 ( subtract 2x from both sides )
- 2 > 2x + 6 ( subtract 6 from both sides )
- 8 > 2x ( divide both sides by 2 )
- 4 > x , thus
x < - 4
Denise has $4.25 and needs to buy school supplies. She has a package of pencils that costs $1.75, a notebook that costs $1 and some erasers (x) that costs $0.25 each. At most, how many erasers can denise buy?
Answers
Answer:
6 erasers
Step-by-step explanation:
The pencils and the notebook together cost $2.75, from there you can calculate how many erasers.
1 eraser would bring the total to $3, therefore Denise can buy $1.25 more of erasers which is 5. 3 + 1.25 is $4.25. therefore Denise can buy 6 erasers
Answer:
he can buy 6 erasers
Step-by-step explanation:
because if you add 1.75 plus one and add 0.25 ....6 times it will equal 4.25 i hope this was helpful
Moates Corporation has provided the following data concerning an investment project that it is considering:
Initial investment $380,000
Annual cash flow $133,000 per year
Expected life of the project 4 years
Discount rate 13%
The net present value of the project is closest to:
a. $(247,000)
b. $15,542
c. $380,000
d. $(15,542)
Answers
The closest option to the calculated net present value is d. $(15,542).
To calculate the net present value (NPV) of the project, we need to discount the annual cash flows to their present value and subtract the initial investment.
Using the formula for the present value of a cash flow:
PV = CF / (1 + r)^n
Where PV is the present value, CF is the cash flow, r is the discount rate, and n is the number of years.
For the given data:
Initial investment = $380,000
Annual cash flow = $133,000 per year
Expected life of the project = 4 years
Discount rate = 13%
Calculating the present value of the annual cash flows:
PV = $133,000 / (1 + 0.13)^1 + $133,000 / (1 + 0.13)^2 + $133,000 / (1 + 0.13)^3 + $133,000 / (1 + 0.13)^4
PV ≈ $133,000 / 1.13 + $133,000 / 1.28 + $133,000 / 1.45 + $133,000 / 1.64
PV ≈ $117,699 + $104,687 + $91,724 + $81,098
PV ≈ $395,208
Finally, calculating the net present value:
NPV = PV - Initial investment
NPV ≈ $395,208 - $380,000
NPV ≈ $15,208
To know more about present value,
https://brainly.com/question/7254007
#SPJ11
Jose is making quarter pound hamburgers for his friends at a cookout. How much hamburger meat will he need in all to make the hamburgers for himself and his five friends .
Answers
Answer:
1.5 Pounds
Step-by-step explanation:
Assuming that they only get 1 quarter-pound burger it would be 6/4 which is one and one-half. He and Five friends makes a total of 6 people.
I don’t remember how to do this.

Answers
The value of x from each diagram is;
a. 21b. 21c. 40d. 52e. 30f. 32h. 35What is the value of x from each diagram?(6x - 24)° + (2x + 12)° = 180°
The sum of angle on a straight line is 180°
6x - 24 + 2x + 12 = 180
8x - 12= 180
8x = 180 - 12
8x = 168
x = 168/8
x = 21
(2x + 17)° = (3x - 4)°
Alternate angles are equal
2x + 17 = 3x - 4
2x - 3x = -4 - 17
-x = -21
x = 21
3x° + (x - 20)° = 180°
Alternate interior angles are equal to 180°
3x + x - 20 = 180
4x - 20 = 180
4x = 180 + 20
4x = 200
x = 40
(x + 24)° + 2x° = 180°
Alternate interior angles are equal to 180°
x + 24 + 2x = 180
3x + 24 = 180
3x = 180 - 24
3x = 156
x = 52
(2x - 10)° = (x + 40)°
Vertical opposite angles are equal
2x - 10 = x + 40
2x - x = 40 + 10
x = 30
(3x - 10)° + (2x + 30)° = 180°
The sum of angle on a straight line is 180°
3x - 10 + 2x + 30 = 180.
5x + 20 = 180
5x = 180 - 20
5x = 160
x = 160/5
x = 32
(x - 15)° + 2x° = 90°
Complementary angles
x - 15 + 2x = 90
3x - 15 = 90
3x = 90 + 15
3x = 105
x = 105 /3
x = 35
Read more on vertical opposite angles:
https://brainly.com/question/68367
#SPJ1
there are 3,681 students at west school. Three grades attend this school. There are the same number of students in each grade. How many students are in each grade.
Answers
Explanation: 3,681 divided by 3 is 1,227
Answer:
1,227
Step-by-step explanation:
3,000 divided by 3 is 1,000
600 divided by 3 is 200
80 divided by 3 is 26 r2
1 + r2 =3
and 3 divided by 3 is 1
1,000 + 200 + 26 + 1 = 1,227
what is the greatest whole number that satisfies the inequality 3x -1 < 8 ?
Answers
Answer:
8
Step-by-step explanation:
3x is a varable and -1 is an integer
Solve: -7 = –1 + x/3
Answers
Answer:
-18
Step-by-step explanation:
-7=-1+x/3
-6=x/3
x=-18
half the product of v and 7
Answers
yikess i need help again

Answers
Draw points at -2 and 5 on the number line
12/(-6) = -2
(-15)/(-3) = 5
1.-2
2.5
-15 divided by -3 would be 5 since their both negitive number the answer would be positive
and 12 divided by -4 would be negitive since one number is positive and the other is negitive
Elijah is ordering a taxi from an online taxi service. The taxi charges $2 just for the
pickup and then an additional $1.50 per mile driven. How much would a taxi ride
cost if Elijah is riding for 9 miles? How much would a taxi ride cost that is m miles
long?
Cost of ride, 9 miles:
Cost of ride, m miles:
Answers
The cost of a taxi ride that is m miles long can be represented by the equation: Cost of ride, m miles = $2 + $1.50m
To calculate the cost of a taxi ride for 9 miles, we need to consider the fixed pickup cost of $2 and the additional cost per mile driven, which is $1.50.
For the 9-mile ride, the additional cost would be:
Additional Cost = $1.50 per mile × 9 miles = $13.50
Adding the pickup cost and the additional cost gives us the total cost of the ride:
Total Cost = Pickup Cost + Additional Cost = $2 + $13.50 = $15.50
Therefore, the cost of the taxi ride for 9 miles would be $15.50.
For a taxi ride that is m miles long, we can use the same formula. The additional cost would be:
Additional Cost = $1.50 per mile × m miles = $1.50m
The total cost of the ride would then be:
Total Cost = Pickup Cost + Additional Cost = $2 + $1.50m
This formula allows us to calculate the cost of the taxi ride for any given number of miles, represented by the variable m.
For more such questions on equation
https://brainly.com/question/29174899
#SPJ8
1.
Solve for x=
35, 103

Answers
Given:
A figure of a circle with secants intersecting inside the circle.
To find:
The value of x.
Solution:
According to the intersection theorem of secants, if two secants intersect each other inside the circle, then the angle on the intersection is the average of the intercepted arcs.
Using the intersection theorem of secants, we get
\(x^\circ=\dfrac{1}{2}(35^\circ+103^\circ)\)
\(x^\circ=\dfrac{1}{2}(138^\circ)\)
\(x^\circ=69^\circ\)
\(x=69\)
Therefore, the value of x is 69.
What is the product of (3x - 4) and (3x - 4)
Answers
Answer:
\( {9x}^{2} - 24x + 6\)
Step-by-step explanation:
i explain in the photo :D

1. given the bilateral z- transform: ???????? (z) = z 2 (z 2−1/4) a) (3 points) find the partial fraction expansion: ???????? (z) = K1 z z−???? + K2 z z−???? show work.
Answers
The partial fraction expansion of the given bilateral z-transform expression is to be found. It can be expressed as ???????? (z) = K1 z / (z - ???? ) + K2 z / (z - ???? ). The steps to determine the values of K1 and K2 will be explained.
To find the partial fraction expansion of the given expression, we first factorize the denominator as (z - ???? )(z - ???? ), where ???? and ???? are the roots of the denominator. In this case, the roots are 1/2 and -1/2.
Next, we express the expression as a sum of two fractions, with each fraction having a distinct root in the denominator. The partial fraction expansion can be written as:
???????? (z) = K1 z / (z - 1/2) + K2 z / (z + 1/2)
To determine the values of K1 and K2, we can multiply both sides of the equation by the common denominator (z - 1/2)(z + 1/2) and equate the numerators. This gives us:
z 2 (z 2 - 1/4) = K1 z(z + 1/2) + K2 z(z - 1/2)
Expanding and collecting like terms, we get:
z 2 (z 2 - 1/4) = (K1 + K2)z 2 + (K1/2 - K2/2)z
By comparing the coefficients of like powers of z on both sides, we can determine the values of K1 and K2. Equating the coefficients, we have:
K1 + K2 = 1
K1/2 - K2/2 = -1/4
Solving these equations simultaneously, we can find the values of K1 and K2, which will complete the partial fraction expansion.
Learn more about coefficients here:
https://brainly.com/question/13431100
#SPJ11
A certain system can experience three different types of defects. Let A i
(i=1,2,3) denote the event that the system has a defect of type i. Suppose that P(A 1
)=0.34,P(A 2
)=0.4,P(A 3
)=0.44
P(A 1
∪A 2
)=0.64,P(A 1
∪A 3
)=0.68
P(A 2
∪A 3
)=0.72,P(A 1
∩A 2
∩A 3
)=0.02
(a) Find the probability that the system has exactly 2 of the 3 types of defects. (b) Find the probability that the system has a type 1 defect given that it does not have a type 2 defect and does not have a type 3 defect.
Answers
(a) The probability that the system has exactly 2 of the 3 types of defects cannot be determined with the given information.
(b) The probability cannot be determined without additional information or assumptions.
(a) The probability that the system has exactly 2 of the 3 types of defects can be calculated using the principle of inclusion-exclusion. We need to find P(A1 ∩ A2' ∩ A3') ∪ P(A1' ∩ A2 ∩ A3') ∪ P(A1 ∩ A2 ∩ A3').
The probability that the system has exactly 2 of the 3 types of defects is 0.08.
Let's break down the calculation step by step. We know the following probabilities:
P(A1) = 0.34, P(A2) = 0.4, P(A3) = 0.44,
P(A1 ∪ A2) = 0.64, P(A1 ∪ A3) = 0.68, P(A2 ∪ A3) = 0.72,
P(A1 ∩ A2 ∩ A3) = 0.02.
To find P(A1 ∩ A2' ∩ A3'), we can subtract the probability of the other cases from P(A1):
P(A1 ∩ A2' ∩ A3') = P(A1) - P(A1 ∩ A2) - P(A1 ∩ A3) + P(A1 ∩ A2 ∩ A3)
= 0.34 - 0.64 - 0.68 + 0.02
= -0.96.
Similarly, P(A1' ∩ A2 ∩ A3') and P(A1 ∩ A2 ∩ A3') can be calculated:
P(A1' ∩ A2 ∩ A3') = P(A2 ∩ A3) - P(A1 ∩ A2 ∩ A3)
= 0.72 - 0.02
= 0.70.
P(A1 ∩ A2' ∩ A3') + P(A1' ∩ A2 ∩ A3') + P(A1 ∩ A2 ∩ A3') = -0.96 + 0.70 + 0.02 = -0.24.
Since probabilities cannot be negative, we can interpret -0.24 as an error in calculations. It is likely due to overlapping information or inconsistent data.
To correct this, we need to revise the given probabilities or check for any inconsistencies in the provided information. Without further clarification or corrections, we cannot determine a valid probability for the system having exactly 2 of the 3 types of defects.
(b) The probability that the system has a type 1 defect given that it does not have a type 2 defect and does not have a type 3 defect can be calculated using conditional probability.
The probability that the system has a type 1 defect given the absence of type 2 and type 3 defects cannot be determined without additional information or assumptions.
We are given the probabilities P(A1), P(A2), P(A3), P(A1 ∪ A2), P(A1 ∪ A3), P(A2 ∪ A3), and P(A1 ∩ A2 ∩ A3), but we do not have any direct information about the conditional probabilities involved in this question. Without knowledge of conditional probabilities or any further information, we cannot calculate the desired probability.
To determine the probability of a type 1 defect given the absence of type 2 and type 3 defects, we would need additional data or assumptions about the relationships between the events A1, A2, and A3. Without such information, we cannot provide a valid answer to this question.
It is important to note that in probability problems, the accuracy and consistency of the given information are crucial for obtaining meaningful results.
To learn more about probability, click here: brainly.com/question/12594357
#SPJ11
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases. *
Answers
On solving the provided question, we can say that the spherical balloon's initial radius is 7 cm.; the final radius is 14 cm. ratio = (7/14) ^2 = 1:4
what is radius?The length of a circle or sphere, in more contemporary use, is the same as its radius in classical geometry, which is one of the line segments from its center to its circumference. The Latin word radius, which also refers to the spokes of a wagon wheel, gave rise to the term. The distance a circle's center is from any point on its perimeter is its radius. Usually, "R" or "r" is used to indicate it. A radius is a line segment that has one endpoint in the center and one on the circumference of a circle. Circular diameter equals radius The diameter of a circle is the segment that traverses its center and has ends that are on the circle.
The spherical balloon's initial radius is 7 cm.
The final radius is 14 cm.
ratio =
(7/14) ^2 = 1:4
To know more about radius visit:
https://brainly.com/question/28946570
#SPJ4
r + 4 > 13 - 2r solve each inequality.
Answers
Hope this helps!!!!!
In 9 hours, Donna reads 45 chapters of a book. What is her rate in chapters per hour?
Answers
Answer:
Donna reads an average of 5 chapters each hour.
Step-by-step explanation:
45/9=5
Need Help here Please!

Answers
Answer:
Step-by-step explanation:

To solve the given equation \(\sf x - y = 4 \\\), we can perform the following calculations:
a) To find the value of \(\sf 3(x - y) \\\):
\(\sf 3(x - y) = 3 \cdot 4 = 12 \\\)
b) To find the value of \(\sf 6x - 6y \\\):
\(\sf 6x - 6y = 6(x - y) = 6 \cdot 4 = 24 \\\)
c) To find the value of \(\sf y - x \\\):
\(\sf y - x = - (x - y) = -4 \\\)
Therefore:
a) The value of \(\sf 3(x - y) \\\) is 12.
b) The value of \(\sf 6x - 6y \\\) is 24.
c) The value of \(\sf y - x \\\) is -4.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
8. Find the length of the unknown side. Round your
answer to the nearest tenth.
10 ft
A. 13.5 A
B. If
C. 4.4 ft
D. 19 ft

Answers
Answer:
the answer is C 4.4 ft hope it helps
Step-by-step explanation:
.4
Similar triangles JKL and NOP, with dimensions in centimeters (cm), are shown.
+
4 cm
K 4 cm
2 cm
J 4 cm
N
What is the length, in centimeters, of side OP?
PLEASE HURRY JDJDJDJNDND

Answers
The length in centimeters of side OP is 8.
Properties of similar triangles.A triangle is a plane figure which is bounded by three straight sides, and has a sum of its internal angle to be 180^o.
Two or more triangles can be referred to as similar if the corresponding sides and measure of corresponding internal angles have some common properties on comparison.
Thus on comparing the corresponding sides of the two given similar triangles, we have;
JK/ ON = KL/ OP
2/ 4 = 4/ OP
2OP = 4*4
= 16
OP = 16/ 2
= 8
OP = 8 cm
Therefore, the length of side OP is 8 cm.
Learn more about the properties of similar triangles at https://brainly.com/question/27996834
#SPJ1
I need help due tomorrow

Answers
Answer:
area= -15 perimeter= 18.810
Step-by-step explanation:
6. What's the product of 3 2/3 and 14 2/5 ?
A. 52 415
B. 42 45
C. 54
D. 52 45
Answers
Answer:
D. 52 45
Step-by-step explanation: