Write a story problem that can be solved by dividing 14.28 by 3.
Answers
Answer: Emily needs a piece of PVC pipe that has a 14.28 diameter but the problem is that she needs 3 pieces.
Step-by-step explanation:
Related Questions
A sheet of custom-size copy paper measures 3.5 in. by 17 in. If a ream (500 sheets) of this paper
has a volume of 119 in.³, how thick is the ream?
Answers
Answer: 2
Step-by-step explanation:
Volume = Base Area x Height
119 = 3.5 * 17 * Height
= 59.5 * Height
119/59.5 = 2
The height/thickness of the ream is 2 in
equations c= 5/9(F-32

Answers
When the temperature is 30° in Celsius, the temperature in Fahrenheit is 86.
What is an equation?An equation is a combination of different variables, in which two mathematical expressions are equal to each other.
The given equation to find the temperature,
C= 5/9(F-32) (1)
Here, C represents the temperature in Celsius,
And F represents the temperature in Fahrenheit.
To find the temperature in Fahrenheit, when C = 30°,
Substitute C = 30° in equation (1),
30 = 5/9(F - 32)
6 x 9 = F - 32
54 = F - 32
F = 86
The temperature in Fahrenheit is 86.
To know more about Equation on:
https://brainly.com/question/187506
#SPJ1
I am really confused what a mean is in math
Answers
Answer:
A mean in math is when you have a set of numbers, you add up all numbers of the set and then divide that sum by the total amount of numbers.
Example: 3,6,8,9
3+6+8+9=26
26/4 (because there is four numbers)
26/4= 6.5
So the mean of that set will be 6.5
Step-by-step explanation:
A bicycle wheel makes five rotations. The bicycle travels ft. Find the diameter of the wheel in inches. Use 3.14 for .
Answers
Answer:
\(r=\frac{L}{2pi R}\)
Diameter=2r
inches=12*ft
Step-by-step explanation:
You forgot to say how far the bike travels.
Given R rotations, L feet, and a wheel radius of r, then the relationship is
\(L=2\pi rR\)
Solving this for r gives
\(r=\frac{L}{2pi R}\)
Diameter=2r
inches=12*ft
Simplify -2.9f + .9f -12 - 4
Answers
\(\huge\text{Hey there!}\)
\(\large\text{-2.9f + 0.9f -12 - 4}\\\\\large\text{COMBINE the LIKE TERMS}\\\\\large\text{(-2.9f + 0.9f) + (-12 - 4)}\\\\\large\text{(-2.9f + 0.9f) = \bf{-2f}}\\\\\large\text{(-12 - 4) = \bf{-16}}\\\\\large\text{= \bf{-2f - 16}}\\\\\\\boxed{\boxed{\large\text{Answer: \bf{-2f - 16}}}}\huge\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
The graph of a piecewise function is shown.
What is the range of the function?

Answers
Answer:
(c) (-∞, -2] ∪ (-1, ∞)
Step-by-step explanation:
You want the range of the piecewise function shown in the graph.
RangeThe range is the vertical extent of the graph, the set of possible output values of the function.
This graph shows a gap between y = -2 and y = -1. The value y = -2 is included in the range, but the value y = -1 is not. (That's what the open circle means.)
Hence, the range is ...
(-∞, -2] ∪ (-1, ∞)

If a trader gained 15% by selling an
article for A1560.00, what is the cost
price of the article?
Answers
Answer$67
Step-by-step explanation:
Answer:
A or B
Step-by-step explanation:
The box plots display data collected when two teachers asked their classes how many pencils they lose in a school year.
A box plot uses a number line from 5 to 47 with tick marks every one unit. The box extends from 8 to 14 on the number line. A line in the box is at 11. The lines outside the box end at 7 and 45. The graph is titled Mr. Johnson's Class, and the line is labeled Number Of Pencils.
A box plot uses a number line from 0 to 51 with tick marks every one unit. The box extends from 12 to 21 on the number line. A line in the box is at 14.5. The lines outside the box end at 0 and 50. The graph is titled Mr. Simpson's Class, and the line is labeled Number Of Pencils.
Which class lost the most pencils overall based on the data displayed?
Mr. Simpson's class; it has a larger median value 14.5 pencils
Mr. Johnson's class; it has a larger median of 11 pencils
Mr. Simpson's class; it has a narrow spread in the data
Mr. Johnson's class; it has a wide spread in the data
Answers
Answer:
A) Mr. Simpson's class; it has a larger median value 14.5 pencils.
Step-by-step explanation:
A box plot is a visual display of the five-number summary:
Minimum value = The value at the end of the left whisker.Lower quartile (Q₁) = The left side of the box.Median (Q₂) = The vertical line inside the box.Upper quartile (Q₃) = The right side of the boxMaximum = The value at the end of the right whisker.From inspection of the box plots (attached), the measures of central tendency (median) and dispersion (range and IQR) are:
Mr Johnson's class:
Median = 11IQR = Q₃ - Q₁ = 14 - 8 = 6Range = max - min = 45 - 7 = 38Mr Simpson's class:
Median = 14.5IQR = Q₃ - Q₁ = 21 - 12 = 9Range = max - min = 50 - 0 = 50In a box plot, the median is a measure of central tendency and tells us the location of the middle value in the dataset. It divides the data into two equal halves, with 50% of the values falling below the median and 50% above it.
The median number of pencils lost in Mr Simpson's class is greater than the median number of pencils lost in Mr Johnson's class. Therefore, Mr. Simpson's class has a larger median value.
The spread of data in a dataset can be measured using both the range and the interquartile range (IQR).
As Mr Simpson's class has a greater IQR and range than Mr Johnson's class, the data in Mr Simpson's class is more spread out than in Mr Johnson's class.
In summary, as Mr Simpson's class has a larger median 14.5 and a wider spread of data, then Mr Simpson's class lost the most pencils overall.

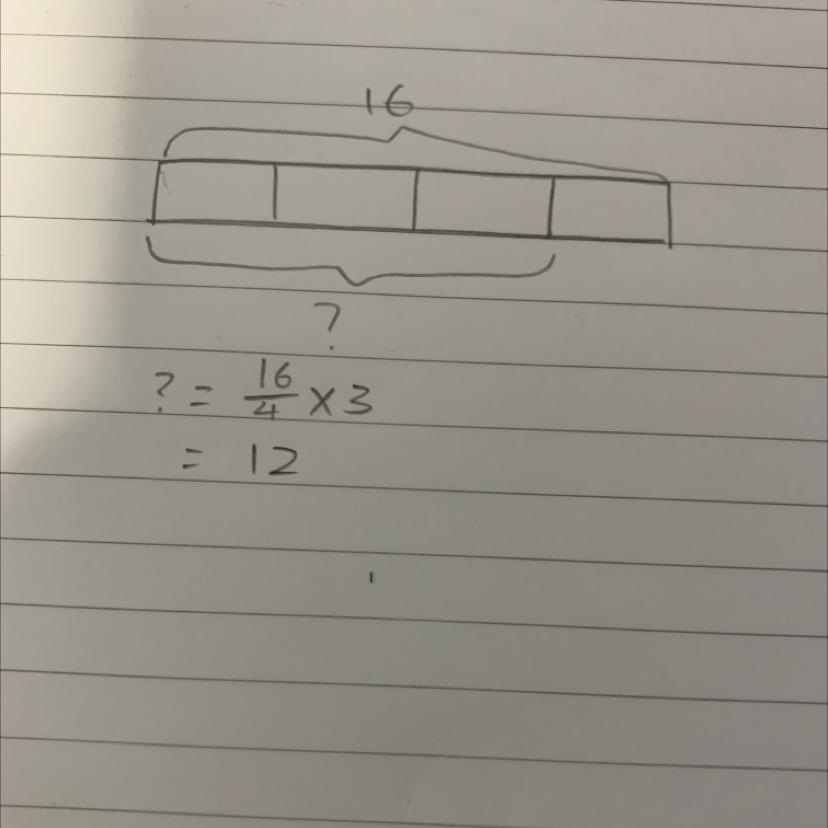
Draw a model to show 3/4 of 16.
Answers
Answer:
Draw a box and split it into four pieces. Write 4 in each of those pieces. Put a "{" or "}" around 3 of them. Next to it write. 4 x 3 OR 4 + 4 + 4 = 12
Step-by-step explanation:
Draw a box and split it into four pieces. Write 4 in each of those pieces. Put a "{" or "}" around 3 of them. Next to it write. 4 x 3 OR 4 + 4 + 4 = 12
Hope that helps!
Convert 3.5 x 10^4 Please help asap
Answers
Answer:
35000
Step-by-step explanation:
Scientific Notation: x × 10ⁿ
We simply use the base 10 decimal system to convert from scientific notation to standard form:
3.5 × 10⁴ means we move the decimal place 4 times to the right.
35 × 10³ = 350 × 10² = 3500 × 10¹ = 35000
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
This graph shows a relationship between the height of a giraffe and its weight. Height versus Weight of Giraffes 1600 1400 1200 800 Weight (kg) 600 400 200 0 1 2 3 4 5 6 Height (m) Which term describes the dashed line shown in the graph? O A. Frequency distribution line O B. Line of central tendency O C. Dependent variable line O D. Line of best fit

Answers
The dash line represents the line of best fit. So the answer is
D. Line of best fit
What operation would isolate the variable? X + 8 = 14
Answers
Answer:
X = 6
Step-by-step explanation:
X + 8 = 14 * Subtract 8 from both sides so that
-8 -8 the 8 is cancelled out
_________
X + 0 = 6
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
HELP! WILL GIVE BRAINLIEST IF YOUR ANSWER IS RIGHT Maria lives in Mexico. Both of her parents are Mexican. Maria is a Mexican citizen. She was born in an American hospital when her parents were on a short vacation in San Diego, California. Was Maria an American citizen at birth? Explain your answer.
Answers
Yes, Maria was a "citizen" of America.
What is citizenship?A legal status and relation between an individual and a state that entails specific legal rights and duties.
Given that, Maria lives in Mexico. Both of her parents are Mexican. Maria is a Mexican citizen. She was born in an American hospital when her parents were on a short vacation in San Diego, California.
The answer is yes,
A child born in American soil will be an American citizen.
Hence, Maria an American citizen at birth.
For more references on citizenship, click;
https://brainly.com/question/18099945
#SPJ2
The fairs train ride covers a distance of 3 miles in 20 minutes what is the speed for the ride in miles per hour?
Answers
Answer:
20/60=1/3
R= d/t
R=3/ \(1/3\)
R=9
Step-by-step explanation:
Aleks topic please help

Answers
Answer:
Item price now= 3.95
Step-by-step explanation:
To find out the price now, we will subtract 79 (original price) by 95% of 75. That will equal the discounted price. Finding the percentage of anything, we can use the formula, Total amount•percentage/100. The total amount is 79, and the percentage is 95. 79•95=7505, 7505/100=75.05. Now, 95% of 79 is 75.05, 79-75.05=3.95. $3.95 is the price now of the item. Though, I am unsure what a ALEKS calculator is. Have a nuce time, and joyful day
\( \rm \int_{ \infty }^{ - \infty } \frac{ { {e}^{ { - x}^{2} } }(5 {x}^{2} + 2 {x}^{4} )}{ {x}^{2}( {x}^{2} + 1)} dx \\ \)
Answers
Consider the integral
\(\displaystyle \int_{-\infty}^\infty \frac{5 + 2x^2}{1 + x^2} e^{-x^2} \, dx\)
which is the negative of yours. Bit strange to integrate over \((\infty,-\infty)\), but if that's what you actually intended, just multiply the final result by -1. Of course, I've already canceled the superfluous factors of \(x^2\).
Expand the integrand into partial fractions.
\(\displaystyle \int_{-\infty}^\infty \frac{5 + 2x^2}{1 + x^2} e^{-x^2} \, dx = \int_{-\infty}^\infty \left(2 + \frac3{1+x^2}\right) e^{-x^2} \, dx\)
Recall that for \(\alpha>0\),
\(\displaystyle \int_{-\infty}^\infty e^{-\alpha x^2} \, dx = \sqrt{\frac\pi\alpha}\)
Now let
\(\displaystyle I(a) = \int_{-\infty}^\infty \frac{e^{-ax^2}}{1+x^2} \, dx\)
Together, these give
\(\displaystyle \int_{-\infty}^\infty \frac{5 + 2x^2}{1 + x^2} e^{-x^2} \, dx = 2\sqrt\pi + 3I(1)\)
Differentiate \(I(a)\) under the integral sign with respect to \(a\) to obtain a simple linear differential equation.
\(\displaystyle \frac{dI}{da} = -\int_{-\infty}^\infty \frac{x^2 e^{-ax^2}}{1+x^2} \, dx \\\\ ~~~~~~~~ = - \int_{-\infty}^\infty \left(1 - \frac1{1+x^2}\right) e^{-ax^2} \, dx \\\\ ~~~~~~~~ = -\sqrt{\frac\pi a} + I(a)\)
Solve for \(I(a)\) with the initial value \(I(1) = \sqrt\pi\). Using an integrating factor,
\(\displaystyle \frac{dI}{da} - I(a) = -\sqrt{\frac\pi a} \\\\ e^{-a} \frac{dI}{da} - e^{-a} I(a) = -\sqrt{\frac\pi a}\,e^{-a} \\\\ \frac{d}{da}\left[e^{-a} I(a)\right] = -\sqrt{\frac\pi a}\,e^{-a}\)
By the fundamental theorem of calculus,
\(\displaystyle e^{-a} I(a) = e^{-a}I(a)\bigg|_{a=0} - \sqrt\pi \int_0^a \frac{e^{-\xi}}{\sqrt\xi} \, d\xi \\\\ I(a) = \pi e^a - \sqrt\pi \, e^a \int_0^a \frac{e^{-\xi}}{\sqrt\xi} \, d\xi\)
so that
\(\displaystyle I(1) = \pi e - \sqrt\pi\,e \int_0^1 \frac{e^{-\xi}}{\sqrt\xi} \, d\xi\)
Substitute \(t=\sqrt\xi\).
\(\displaystyle I(1) = \pi e - 2\sqrt\pi\,e \int_0^1 e^{-t^2} \, dt\)
Recall the error function,
\(\mathrm{erf}(x) = \displaystyle \frac2{\sqrt\pi} \int_0^x e^{-t^2} \, dt\)
which we can use to write
\(I(1) = \pi e - 2\sqrt\pi e \cdot \dfrac{\sqrt\pi}2\,\mathrm{erf}(1) = \pi e - \pi e \,\mathrm{erf}(1)\)
Finally, we arrive at
\(\displaystyle \int_{-\infty}^\infty \frac{5 + 2x^2}{1 + x^2} e^{-x^2} \, dx = \boxed{2\sqrt\pi + 3\pi e - 3\pi e \, \mathrm{erf}(1)}\)
ig
How much material does he need
Marcus and his dad were going camping. When they went into the garage to get their tent they noticed it was ripped. Marcus dad said he could fix the tent. He would some new material to cover the one rectangular side that ripped.
to cover the one rectangular side of the tent with the rip? Justify
your answer using equations/formulas, models, and/or words to explain your mathematical
reasoning.
IF Marcus dad wanted to re-cover the whole tent including the bottom, how much material would he need? justify your answer using equations/formulas, models, and/or words to explain your mathematical reasoning.
Please help!!

Answers
Answer:
75 and 246
Step-by-step explanation:1) i multiply 10 by 15 to get to get 150 since we are multiplying both sidesw of the tent i cut it in half to get my final answer of 75
2)first what i did was multiply 8 by 18 to get a answer of 96 next i multiply 10 by 15 to get 150 and lasly i add trhe two numbers up to get my final answer 246
I don’t know how to do this question if anyone does please put the steps thank you.

Answers
If the third term is 31, then let's get the second term. We have to use the rule we were given and work backwards. So, we will add three and then divide by 2.
31 + 3 = 34
34 / 2 = 17
17 is the second term. Let's do the same thing we just did to find the first term: add three, divide by 2.
17 + 3 = 20
20 / 2 = 10
Answer: the first term is 10
Hope this helps!
Which equation accurately represents this statement? Select three options. Negative 3 less than 4.9 times a number, x, is the same as 12.8. Negative 3 minus 4.9 x = 12.8 4.9 x minus (negative 3) = 12.8 3 + 4.9 x = 12.8 (4.9 minus 3) x = 12.8 12.8 = 4.9 x + 3
Answers
The value of x in the statement negative 3 less than 4.9 times a number x is the same as 12.8 is 2.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
Given a statement negative 3 less than 4.9 times a number, x, is the same as 12.8 this can be numerically expressed as,
4.9x - (- 3) = 12.8.
4.9x + 3 = 12.8
4.9x = 12.8 - 3.
4.9x = 9.8.
x = 9.8/4.9.
x = 2.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
.3d-1/3 1/3=.84:7/15 I WILL GIVE BRAINLIST TO WHO EVER CAN GET THIS
Answers
Answer:
d = 23 1/3
Step-by-step explanation:
You want to solve the proportion (0.3d -1)/(3 1/3) = (0.84)/(7/15).
Solution\(\dfrac{0.3d-1}{3\dfrac{1}{3}}=\dfrac{0.84}{\dfrac{7}{15}}\qquad\text{given}\\\\\\\dfrac{3(0.3d-1)}{10}=\dfrac{15(0.84)}{7}\qquad\text{invert and multiply}\\\\0.09d -0.3=1.8\qquad\text{simplify}\\\\0.09d = 2.1\qquad\text{add 0.1}\\\\d=\dfrac{2.10}{0.09}=\dfrac{70}{3}\qquad\text{divide by 0.09}\\\\\boxed{d=23\dfrac{1}{3}}\)
__
Check
(0.3·(70/3) -1)/(3 1/3) = 0.84/(7/15)
(7 -1)/(10/3) = 1.8
6(3/10) = 1.8 . . . . . . true
Answer: 23 1/3
Step-by-step explanation:
Use the Distributive Property to correctly rewrite or simplify the expression:
21k+13k+9k
Answers
Answer:
21k+9k+13, and simplified into 43k.
Step-by-step explanation:
The distributive property means that you can put addends or factors in any order to get the same result(9+1=10, 1+9=10)
21k+13k+9k can be re-written into 21k+9k+13, and simplified into 43k.
Answer:
43k
Step-by-step explanation:
Linda, Frank, and Alan served a total of 78 orders Monday at the school cafeteria. Linda served 6 more orders than Alan. Frank served 2 times as many orde as Alan. How many orders did they each serve? Number of orders Linda served:
frank served
Alan served
Answers
Answer:
Frank served 32
Alan served 18
Linda served 24
Step-by-step explanation:
78-6=72
72 divided by 4 = 18
Next time if you need help on these kind of questions, try drawing a bar diagram, it really helps
Find the measure of each angle of the quadrilateral.

Answers
all work should be in the picture, lmk if theres anything confusing

3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
(CLASSKICK) HELP ASAP!!!

Answers
Answer:
94.3
Step-by-step explanation:
You want to know how to fill in the proportion associated with the question, "What is 115% of 82?"
ProportionThe diagram is intended to help you match parts of the question to parts of the proportion. The attachment shows the intended relation.
The solution is found by multiplying both sides by 82:
(x/82)·82 = (115/100)·82
x = 94.3
EquationThe question can also be written as a statement:
"what" is 115% of 82
When written as an equation, "is" means "equals", and "of" means "times":
what = 115% × 82
Of course, you can use any variable name of your choosing in place of "what". In your diagram, that is "x". And, you know how to write a percentage as a fraction or decimal, so this becomes ...
x = 115/100 × 82 = 1.15 × 82
All that remains is to evaluate this expression.
x = 1.15 × 82 = 94.3
So, the answer to the question is ...
94.3 is 115% of 82.

The table shows Avery’s net worth statement.
Net Worth Statement. Item; Value. Bank accounts; $3,900; Car (current value); question mark; Credit card debt; negative $2,950; Real estate; $37,425; Student loans; negative $1,700; Investments; $4,600.
Avery’s net worth is $53,755. Based on the information in the table, what is the current value of Avery’s car?
Answers
The current value of Avery’s car is $12,480.
Current valueFirst step is to calculate the Net Worth
Bank accounts $3,900
Credit card debt ($2,950)
Real estate $37,425
Student loans ($1,700)
Investments $4,600
Net worth $41,275
Second step is to calculate the current value of Avery’s car
Current value=$53,755-$41,275
Current value=$12,480
Inconclusion the current value of Avery’s car is $12,480.
Learn more about current value here:https://brainly.com/question/15904086
Find the third iterate x3 of f(x) = 2x + 3
for an initial value of x0 = 2
a. 7
b. 15
c. 17
d. 37
Answers
For the function f(x) = 2x + 3 the third iterate x₃ is 37
To find the third iterate, x3, of the function f(x) = 2x + 3, given an initial value of x₀ = 2,
we can apply the function repeatedly.
Starting with x₀ = 2:
x₁ = f(x₀)
= 2(2) + 3
= 7
x₂ = f(x₁)
= 2(7) + 3 = 17
x₃ = f(x₂)
= 2(17) + 3
= 37
Therefore, the third iterate x₃ is 37.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ1
A metal bar weighs 9 ounces. 93% of the bar is silver. How many ounces of Iver are in the bar?
Answers
A metal bar weighs 9 ounces.
The weight of the metal bar = 9 ounces
93% of the bar is silver.i.e 93% of 9 ounces is silver
\(\begin{gathered} 93\text{ percent of 9 ounces=}\frac{93\times9}{100} \\ 93\text{ percent of 9 ounces=}8.37\text{ ounces} \end{gathered}\)So, 8.37 ounces are silver
Answer : 8.37 ounces