Which 2 numbers give you -70 when multiplied but when added give you 9?
Answers
The numbers for the condition are 14 and -5.
What is an expression?What is an expression?Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement. It's possible to multiply, divide, add, or subtract with this mathematical operation.
Given two numbers,
let the numbers be a and b,
and the product of a and b is -70.
a x b = -70
a = -70/b
addition of numbers is 9
a + b = 9
substitute value of a
-70/b + b = 9
b² - 9b - 70 = 0
factors of equation are
b² + 5b - 14b - 70 = 0
(b + 5)(b - 14) = 0
b = -5 and b = 14
when b = -5, a = 14
and when b = 14, a = -5
Hence the numbers are -5 and 14.
Learn more about expressions;
https://brainly.com/question/29169334
#SPJ1
Related Questions
I need help first answer gets brainliest

Answers
To find which fractions are equal to each other, we must simplify or multiply to both denominator and numerator:
\(\frac{2}{6} =\frac{1*2}{3*2} =\frac{1}{3}*\frac{2}{2}=\frac{1}{3}*1= \frac{1}{3} \\\\\frac{8}{1}=8\\ \\\frac{2}{4} =\frac{1*2}{2*2} =\frac{1}{2}*\frac{2}{2} =\frac{1}{2} *1= \frac{1}{2} =\frac{1}{2}*1 =\frac{1}{2}*\frac{4}{4} =\frac{1*4}{2*4}=\frac{4}{8} \\\\\frac{2}{8} =\frac{1*2}{4*2}=\frac{1}{4}*\frac{2}{2} =\frac{1}{4} *1 =\frac{1}{4} \\\\\frac{4}{4} =1\)
Hope that helps!
Answer:
2/6 = 1/3
8/1 = 8
2/4 = 4/8
2/8 = 1/4
4/4 = 1
Step-by-step explanation:
2/2 = 1 and 6/2 = 3 so that would make the equivalent fraction 1/3
for 8/1 it is the same as just 8
2*2 = 4 and 4*2 = 8 so that would make the equivalent fraction 4/8
and 2/8 is 1/4
and 4/4 is just 1
PLEASE RATE!! I hope this helps!!
If you have any questions let me know
a 0.250–a current is charging a capacitor that has circular plates 10.8 cm in radius. the plate separation is 4.00 mm. (a) What is the time rate of increase of electric field between the plates? (b) What is the magnetic field between the plates 5.00 cm from the center?
Answers
The magnetic field between the plates is at a distance of 5.00 cm from the center.
To solve this problem, we can use the formulas for the electric field and magnetic field due to a charging capacitor.
(a) The time rate of increase of the electric field between the plates can be found using the formula:
dE/dt = (I / (πε₀R²)),
where dE/dt is the time rate of increase of the electric field, I is the current, ε₀ is the permittivity of free space, and R is the radius of the circular plates.
Given:
I = 0.250 A (current)
R = 10.8 cm = 0.108 m (radius)
Using the formula, we can calculate the time rate of increase of the electric field:
dE/dt = (0.250 A) / (π * ε₀ * (0.108 m)²)
The value of ε₀ is approximately 8.854 × 10^(-12) F/m.
Plugging in the values:
dE/dt = (0.250 A) / (π * (8.854 × 10^(-12) F/m) * (0.108 m)²)
Calculating this expression will give you the time rate of increase of the electric field between the plates.
(b) To calculate the magnetic field between the plates 5.00 cm from the center, we can use Ampere's law:
B = (μ₀I) / (2πr),
where B is the magnetic field, I is the current, μ₀ is the permeability of free space, and r is the distance from the center of the circular plates.
Given:
I = 0.250 A (current)
r = 5.00 cm = 0.05 m (distance from the center)
Using the formula, we can calculate the magnetic field:
B = (μ₀ * 0.250 A) / (2π * 0.05 m)
The value of μ₀ is approximately 4π × 10^(-7) T·m/A.
Plugging in the values:
B = (4π × 10^(-7) T·m/A * 0.250 A) / (2π * 0.05 m)
Calculating this expression will give you the magnetic field between the plates at a distance of 5.00 cm from the center.
To know more about magnetic fields visit:
https://brainly.in/question/18238294
#SPJ11
Two similar blocks have corresponding edges of length 10cm and 20cm.find the ratio of their masses
Answers
selling price per unit $ 120 $ 160 variable costs per unit 40 90 contribution margin per unit $ 80 $ 70 machine hours per unit 1 hour 2 hours maximum unit sales per month 600 units 200 units
Answers
For a product with a selling price per unit of $120 and $160, variable costs per unit of $40 and $90, and maximum unit sales per month of 600 and 200 units, the contribution margin per unit is $80 and $70, respectively.
The contribution margin per unit is calculated by subtracting the variable costs per unit from the selling price per unit. For the first product, the contribution margin per unit is $120 - $40 = $80, while for the second product, it is $160 - $90 = $70.
The contribution margin per unit represents the amount of money available to cover fixed costs and contribute to the company's profit. A higher contribution margin per unit indicates a higher profitability for the product.
Considering the maximum unit sales per month, the first product has a higher sales potential with a maximum of 600 units compared to the second product's maximum of 200 units. Therefore, the first product has a higher total contribution margin, which suggests greater profitability compared to the second product.
In conclusion, based on the given information, the first product with a selling price per unit of $120, variable costs per unit of $40, and a higher maximum unit sales per month of 600 units, has a higher contribution margin per unit of $80, indicating higher profitability compared to the second product.
Learn more about contribution margin per unit here:
https://brainly.com/question/31484547
#SPJ11
The difference between the high and low temperatures on Sunday was at least 35°F. The low temperature on Sunday was -8°F.
Part A
Select the correct values and symbol to write an inequality that represents the possible high temperatures, t, on Sunday.
t- __ _ __
Answers
High temp ≥ Low temp + difference
High temp ≥ -8°F + 35°F
High temp ≥ 27°F
InequalityAn inequality is a relationship between two different quantities or expressions.
An inequality may be expressed by a mathematical sentence that uses the following symbols:
< is less than
> is greater than
≤ is less than or equal to
≥ is greater than or equal to
≠ is not equal to
To learn more about inequalities, read more here: https://www.bing.com/ck/a?!&&p=dc838390ec092130JmltdHM9MTY3Njg1MTIwMCZpZ3VpZD0wZWI0MGNjYi04NDg2LTY1ZTgtMzE4OS0xZTczODU5YjY0YmQmaW5zaWQ9NTE1Ng&ptn=3&hsh=3&fclid=0eb40ccb-8486-65e8-3189-1e73859b64bd&psq=Inequality+site%3ahttps%3a%2f%2fbrainly.com+in+text%3a+verified+%3amathematics&u=a1aHR0cHM6Ly9icmFpbmx5LmNvbS9xdWVzdGlvbi8yNTQzODE0OQ&ntb=1
#SPJ1
2.
020
Topic 8.3: Area and Circumference of Circles
Use the information provided to answer the following questions for the circles below.
1.
1a. Area of circle in terms of TT:
8 in
1b. Circumference of circle in terms of TT:
2a. Area of circle in terms of TT:
2b. Circumference of circle in terms of TT:
6ft
Answers
Area and Circumference of Circles. Here's the step-by-step explanation for each circle:
Circle 1:
Radius: 8 in
1a. Area of circle in terms of π:
Area = π * (radius^2)
Area = π * (8^2)
Area = 64π square inches
1b. Circumference of circle in terms of π:
Circumference = 2 * π * radius
Circumference = 2 * π * 8
Circumference = 16π inches
Circle 2:
Radius: 6 ft
2a. Area of circle in terms of π:
Area = π * (radius^2)
Area = π * (6^2)
Area = 36π square feet
2b. Circumference of circle in terms of π:
Circumference = 2 * π * radius
Circumference = 2 * π * 6
Circumference = 12π feet
Your answer:
1a. The area of the first circle in terms of π is 64π square inches.
1b. The circumference of the first circle in terms of π is 16π inches.
2a. The area of the second circle in terms of π is 36π square feet.
2b. The circumference of the second circle in terms of π is 12π feet.
To know more about Circles visit:-
https://brainly.com/question/4637894
#SPJ11
Find the inverse of the linear transformation y_1 = x_1 + 7x_2 y_2 = 3x_1 + 20x_2. In Exercises 9 through 12, decide whether the given matrix is invertible. Find the inverse if it exists. In Exercise 12, the constant k is arbitrary. [1 k 0 1] a. For which values of the constant k is the matrix [2 3 5 k] invertible? b. For which values of the constant k are all entries of [2 3 5 k]^-1 integers?
Answers
a) The matrix is invertible for all values of k except 7.5.
b) The only values of k that make all entries of [2 3 5 k]^-1 integers are 7 and 8.
To find the inverse of a linear transformation, we need to represent it in matrix form. The given linear transformation can be represented as a matrix:
[1 7]
[3 20]
To find the inverse of a matrix, we need to use the formula:
A^-1 = (1/det(A)) * adj(A)
Where det(A) is the determinant of the matrix A and adj(A) is the adjugate (transpose of the cofactor matrix) of A.
Using this formula, we can find the inverse of the given matrix as follows:
det([1 7][3 20]) = (1*20) - (7*3) = 1
adj([1 7][3 20]) = [20 -7][-3 1]
Therefore, the inverse of the matrix is:
[20 -7]
[-3 1]
To check that this is the correct inverse, we can verify that the product of the two matrices is the identity matrix:
[1 7][20 -7] = [1 0]
[3 20][-3 1] [0 1]
For exercise 9, we need to determine if the matrix [1 k 0 1] is invertible. To do this, we can find the determinant of the matrix:
det([1 k][0 1]) = (1*1) - (k*0) = 1
Since the determinant is not equal to zero, the matrix is invertible.
For exercise 12a, we need to find the values of k that make the matrix [2 3 5 k] invertible. To do this, we can again find the determinant of the matrix:
det([2 3][5 k]) = (2*k) - (3*5) = 2k - 15
For the matrix to be invertible, the determinant must be non-zero. Therefore, we need:
2k - 15 ≠ 0
2k ≠ 15
k ≠ 7.5
Therefore, the matrix is invertible for all values of k except 7.5.
For exercise 12b, we need to find the values of k that make all entries of [2 3 5 k]^-1 integers. To do this, we can find the inverse of the matrix:
[2 3][5 k]^-1 = (1/((2*k) - (3*5)))[k -3][-5 2]
We need all entries of this matrix to be integers. Therefore, we need:
1/((2*k) - (3*5)) to be an integer (i.e. the denominator is a factor of 1)
(k - 3)/((2*k) - (3*5)) and -5/((2*k) - (3*5)) to be integers
Simplifying the denominator, we get:
(2*k) - (3*5) = 2k - 15
Therefore, the denominator must be a factor of 1, which means it can only be 1 or -1.
If the denominator is 1, then:
2k - 15 = 1
2k = 16
k = 8
If the denominator is -1, then:
2k - 15 = -1
2k = 14
k = 7
Therefore, the only values of k that make all entries of [2 3 5 k]^-1 integers are 7 and 8.
To learn more about Matrix visit: brainly.com/question/12138961
#SPJ11
what are the images of F and H
Answers
what? there are no images, i have no idea what you are saying
Find the radius of convergence, R, of the series. ∑
n=0
[infinity]
(−1)
n
7n+1
(x−5)
n
R= Find the interval, I, of convergence of the series. (Enter your answer using interval notation I= Find the radius of convergence, R, of the series. R=∑
n=1
[infinity]
(−1)
n
4
n
n
3
x
n
Find the interval, 1 , of convergence of the series. (Enter your answer using interval notation.)
Answers
The series converges for values of x within the interval (-√2/2, √2/2), the radius of convergence, R, is √2/2. The interval of convergence, I, is (-√2/2, √2/2).
To find the radius of convergence, R, of the series, we can use the ratio test. The ratio test states that if the limit of the absolute value of the ratio of consecutive terms in a series is L, then the series converges if L < 1 and diverges if L > 1.
Let's apply the ratio test to the given series:
aₙ = x⁴ⁿ / (n (ln n)⁸)
First, let's find the ratio of consecutive terms:
|rₙ| = |(\(x^{4(n+1)}\)/ ((n+1) (ln(n+1))⁸)) * ((n (ln n)⁸) / x⁴ⁿ)|
|rₙ| = |(x⁴ / (n+1)) * ((ln n)⁸ / (ln(n+1))⁸)|
Now, let's simplify the expression:
|rₙ| = (x⁴ / (n+1)) * ((ln n)⁸ / (ln(n+1))⁸)
Taking the limit as n approaches infinity:
\(lim_{n- > oo}\) |r_n| = \(lim_{n- > oo}\) [(x⁴ / (n+1)) * ((ln n)⁸ / (ln(n+1))⁸)]
Using L'Hôpital's rule to evaluate the limit:
\(lim_{n- > oo}\) [(x⁴ / (n+1)) * ((ln n)⁸ / (ln(n+1))⁸)]
= \(lim_{n- > oo}\) [(4x⁴ / (n+1)) * ((ln n)⁷ / (ln(n+1))⁷ * (1 / (n+1)) / (1 / (n+1))]
= 4x⁴ * \(lim_{n- > oo}\) [((ln n)⁷ / (ln(n+1))⁷ * (1 / (n+1)) / (1 / (n+1))]
= 4x⁴ * \(lim_{n- > oo}\) [(ln n)⁷ / (ln(n+1))⁷]
Now, let's consider the limit as n approaches infinity for the expression inside the parentheses:
\(lim_{n- > oo}\) [(ln n)⁷ / (ln(n+1))⁷]
Since the limit of the logarithm ratio as n approaches infinity is 1:
\(lim_{n- > oo}\) [(ln n)⁷ / (ln(n+1))⁷] = 1
Substituting this back into the previous limit:
\(lim_{n- > oo}\) |rₙ| = 4x⁴ * 1 = 4x⁴
According to the ratio test, the series converges if |rₙ| < 1. Therefore, we have:
4x⁴ < 1
Solving for x:
x⁴ < 1/4
Taking the fourth root of both sides:
x < (1/4)¹
x < 1/√2
x < √2/2
Since the series converges for values of x within the interval (-√2/2, √2/2), the radius of convergence, R, is √2/2. Therefore:
R = √2/2
The interval of convergence, I, is (-√2/2, √2/2), which can be represented in interval notation as:
I = (-√2/2, √2/2)
The complete question is:
Find the radius of convergence, R, of the series.
\(\sum_{n=2}^{oo} x^{4n}/[n(In n)^8]\)
R =?
Find the interval, I, of convergence of the series. (Enter your answer using interval notation.)
I =?
To know more about converges:
https://brainly.com/question/29258536
#SPJ4
Current standards suggest that a single subject research design can demonstrate a functional relation between the independent and dependent variables with a minimum of __________ effects.
Answers
Current standards indicate that a single subject research design should demonstrate a functional relation between independent and dependent variables with a minimum of three effects.
Single subject research designs, also known as single case experimental designs, are experimental designs commonly used in behavioral sciences to study the effects of interventions or treatments on individuals. These designs involve repeated measurement of the dependent variable under different conditions or phases.
To establish a functional relation between the independent and dependent variables, current standards suggest that a minimum of three effects should be demonstrated. These effects typically consist of a baseline phase, an intervention phase, and a return-to-baseline phase. The baseline phase serves as a control condition where the independent variable is absent or has no effect on the dependent variable. The intervention phase introduces the independent variable, and its effects on the dependent variable are observed.
Learn more about relation here:
https://brainly.com/question/31111483
#SPJ11
URGENT PLS HELP. pls but why or why not thank you:))

Answers
Answer:
No the relation is not a function
Step-by-step explanation:
A function by definition will have a unique output for every input, so there should be no repeating outputs, however, the clinic cares for 2 legged animals (birds) as well as 4 legged animals (cats and dogs). With this being said, if a clinic has 2 animals(input), the amount of legs(output) could be 8 if two dogs, or it could be 4 if two birds, or even six if a dog and bird.
If this were a function, the clinic would undeniably have different amounts of legs having two animals opposed to one animal, but this isn't true. if the clinic has 2 birds(input), there'd be 4 legs(output). but the clinic would also have 4 legs(output) if it had 1 dog(input). the output is the same for two different inputs
This shows the output is varying depending on the type of animal since the amount of legs changes, rather than the amount of animals.
Hope this helps :)
Lets=x2ir3|x=(r2s,3r s, s),r,s2ir. show thatsis a subspace of ir3. show that the vectors inslee on the plane with equation 3xy 7z= 0
Answers
Vectors in S satisfy 3xy - 7z = 0 since substituting the components of x = (r²s, 3rs, s) into equation gives 3(r²s)(3rs) - 7s = 9r²s² - 7s = s(9r²s - 7) = 0. This shows vectors in S lie on plane defined by equation 3xy - 7z = 0.
To show that S is a subspace of ℝ³, where S is defined as the set of vectors x = (r²s, 3rs, s) with r, s ∈ ℝ, we need to demonstrate that S satisfies three conditions: it contains the zero vector, it is closed under vector addition, and it is closed under scalar multiplication. Additionally, we need to show that the vectors in S lie on the plane with the equation 3xy - 7z = 0.
First, we verify that S contains the zero vector. Substituting r = 0 and s = 0 into the vector x, we obtain (0, 0, 0), which is the zero vector.
Next, we check if S is closed under vector addition. Let x₁ = (r₁²s₁, 3r₁s₁, s₁) and x₂ = (r₂²s₂, 3r₂s₂, s₂) be two arbitrary vectors in S. Their sum, x = x₁ + x₂, can be expressed as (r₁²s₁ + r₂²s₂, 3r₁s₁ + 3r₂s₂, s₁ + s₂). Since r₁, r₂, s₁, and s₂ are real numbers, the sum of the corresponding components is also a real number. Hence, S is closed under vector addition.
Lastly, we need to show that S is closed under scalar multiplication. Let x = (r²s, 3rs, s) be an arbitrary vector in S and c be a real number. The scalar multiple c · x can be written as (c · r²s, c · 3rs, c · s), which is also in the form of a vector in S. Thus, S is closed under scalar multiplication.
Furthermore, the vectors in S satisfy the equation 3xy - 7z = 0 since substituting the components of x = (r²s, 3rs, s) into the equation gives 3(r²s)(3rs) - 7s = 9r²s² - 7s = s(9r²s - 7) = 0. This shows that the vectors in S lie on the plane defined by the equation 3xy - 7z = 0.
Therefore, based on the verification of the three conditions for a subspace and the vectors satisfying the given equation, S is a subspace of ℝ³.
Learn more about scalar here
brainly.com/question/12934919
#SPJ11
Please help will give brainliest!!!!

Answers
Answer:
answer is c
Step-by-step explanation:
if u add it all up you get answer
which decimal is greater 0.36 or 0.49
Answers
Answer:
0.49
Step-by-step explanation:
Answer:
0.49
Step-by-step explanation:
Suppose the half-life of a decaying radioactive isotope is 674 years. How long will it takefor the isotope to decay from 100 grams to 30 grams? Answer to the nearest hundredthof a year.accc
Answers
The half life formula is :
\(N(t)=N_o(\frac{1}{2})^{\frac{t}{T}}\)where N(t) = remaining quantity after t years
No = Original Quantity
t = time in years
T = half life in years
From the problem, we have :
N(t) = 30 grams
No = 100 grams
T = 674
Solve for t :
\(\begin{gathered} 30=100(\frac{1}{2})^{\frac{t}{674}} \\ \frac{30}{100}=(\frac{1}{2})^{\frac{t}{674}} \\ \frac{3}{10}=(\frac{1}{2})^{\frac{t}{674}} \end{gathered}\)Take ln of both sides :
\(\begin{gathered} \ln (\frac{3}{10})=\ln (\frac{1}{2})^{\frac{t}{674}} \\ \ln (\frac{3}{10})=\frac{t}{674}\ln (\frac{1}{2}) \\ t=\frac{674\ln (\frac{3}{10})}{\ln (\frac{1}{2})} \\ t=1170.71 \end{gathered}\)The answer is t = 1170.71 years
Simplify: (9x - 5)
(9)
Answers
Answer:
81x - 45
Step-by-step explanation:
Use the distributive property
(9x - 5)(9)
= (9x)(9) - (5)(9)
= 81x - 45
Which of the following is a solution of this equation?
A.
(5,0)
B.
(-1, 1)
C.
(3,-1)
D.
(-2,-3)

Answers
Answer:
D. (-2,-3)
Step-by-step explanation:
substitute the point values of \(x\) and \(y\) into the equation \(y=\frac{1}{2}x-2\)
A. \(0=\frac{1}{2}(5)-2\)
\(0=2.5-2\)
\(0\) ≠ \(0.5\)
B. \(1=\frac{1}{2}(-1)-2\)
\(1=-.5-2\)
\(1\) ≠ \(-2.5\)
C. \(-1=\frac{1}{2}(3)-2\)
\(-1=1.5-2\)
\(-1\) ≠ \(-0.5\)
D. \(-3=\frac{1}{2}(-2)-2\)
\(-3=-1-2\)
\(-3=-3\)
At 7:00 pm, the temperature was -7 °F. The next morning the temperature had raised
to 42 °F. How many degrees F. did the temperature change?
Answers
Answer:
49 degrees
Step-by-step explanation
Answer:
I think 49 °F
Step-by-step explanation:
42 - (-7) = 49 °F
So the temperature raised 49 degrees since 7pm last night.
I think thats right. :)
how many ways are there for six ce majors and ten cs majors to stand in a line so that no two ce majors stand next to each other?
Answers
There are 1,207,084,032,000 ways for 6 CE majors and 10 CS majors to stand next to each other in the lines.
We use permutations and combinations for solving this problem. We fix the position of CS students so that they can stand in a fixed place by
= 10! ways (i)
Now, there are 11 places left for CE students so that no two CE students stand next to each other.
6 CE students in the rest of the 11 places can sit by = 11! / (11-6)! ways (ii)
Hence, using the values of (i) and (ii), we get -
= (10! * 11!) / (11-6)!
= 1,207,084,032,000
Therefore, we have 1,207,084,032,000 ways in which the six CE majors and ten CS majors can stand in a line so that no two CE majors stand next to each other.
Learn to know more about Permutations and Combinations on
https://brainly.com/question/13387529?referrer=searchResults
#SPJ4
Which one represents a function? because I can’t tell.
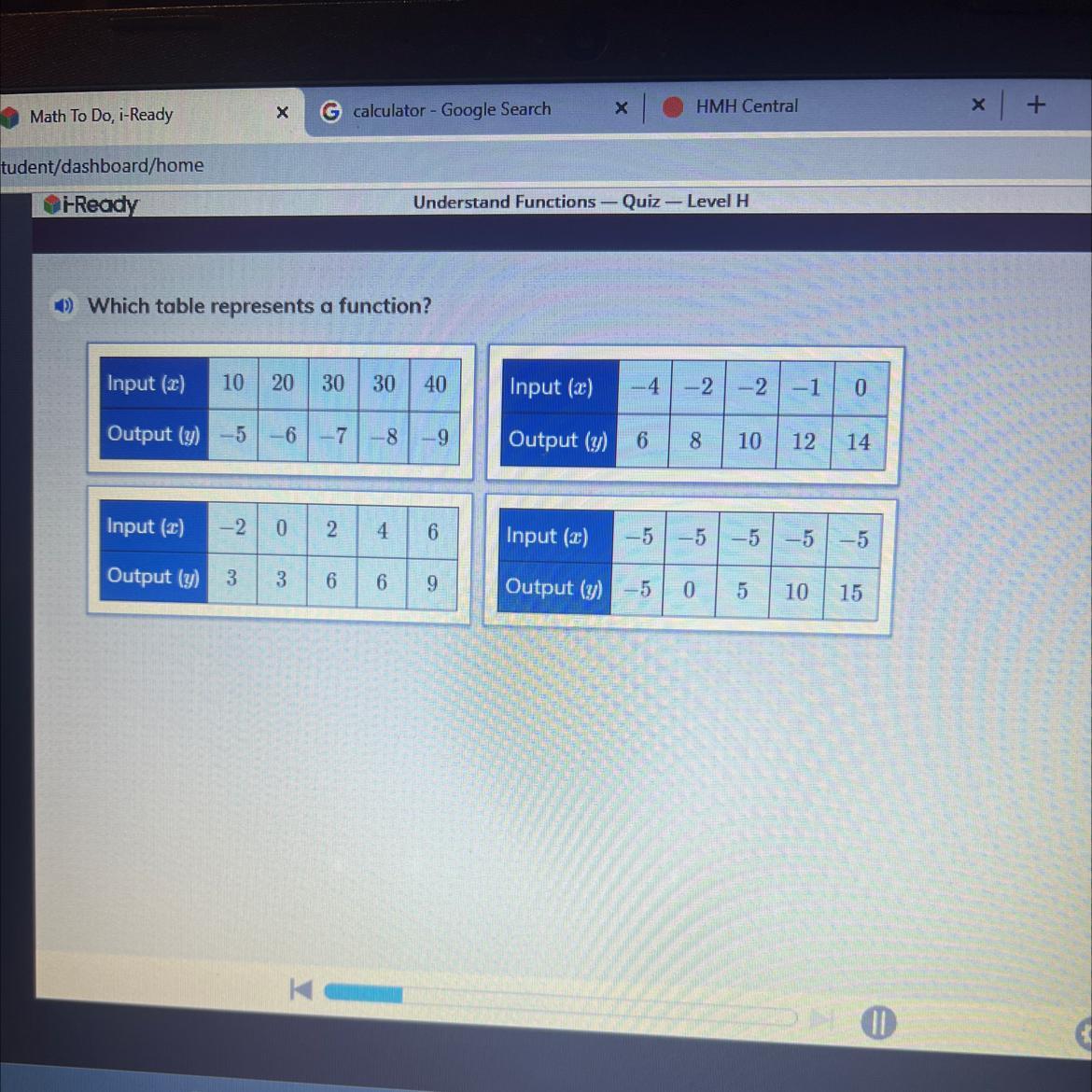
Answers
Answer:
Bottom Left Table
Step-by-step explanation:
So, the easiest way to determine a function is to see if any x factors repeat. In the top left table, 30 repeats. In the top right table, -2 repeats. In the Bottom right table, -5 repeats. But in the bottom left table, none of the x factors repeat.
Question 2 For the following matrix Then [340]
A= [-127]
[-2-44]
(Please use a comma between two numbers.)
(a) The minors M13, M23, M33= 8,-4,10
(b)The cofactors C13, C23,C33= 8,4,10 (c) The determinant det(A) = 68
Answers
For the given matrix A, the minors M13, M23, M33 are 8, -4, and 10 respectively. The cofactors C13, C23, C33 are 8, 4, and 10 respectively. The determinant det(A) is 68.
To find the minors of a matrix, we need to find the determinants of the submatrices obtained by removing the row and column corresponding to the element of interest. In this case, the minors M13, M23, and M33 correspond to the determinants of the 2x2 submatrices obtained by removing the first row and the third column, second row and third column, and third row and third column, respectively.
To find the cofactors, we multiply each minor by a positive or negative sign based on its position in the matrix. The signs alternate starting with a positive sign for the top left element. In this case, the cofactors C13, C23, and C33 correspond to the minors M13, M23, and M33 respectively.
Finally, the determinant of a 3x3 matrix can be found by using the formula det(A) = a11C11 + a12C12 + a13C13, where a11, a12, and a13 are the elements of the first row of the matrix and C11, C12, and C13 are their corresponding cofactors. In this case, the determinant det(A) is 68.
Therefore, the minors M13, M23, M33 are 8, -4, and 10 respectively. The cofactors C13, C23, C33 are 8, 4, and 10 respectively. And the determinant det(A) is 68.
Learn more about submatrices here:
https://brainly.com/question/31669133
#SPJ11
Aiden is replacing the tile in a rectangular kitchen. The length of the kitchen is nine feet shorter than three times its width, w. The perimeter of the kitchen is six times the width. If tiles cost $1.69 a square foot, what is the total costs to tile the kitchen?
Answers
Answer:
Total Cost of tile = $273.28
Step-by-step explanation:
From the given information:
Let the width be = x
Then, the length of the rectangular kitchen is L = 3x - 9
The perimeter is = 6x
Suppose the cost of the tile = $1.69 a square foot.
Then the total costs to tile the kitchen is calculated as follows:
The Perimeter of the rectangle = 2(L + b)
The Perimeter of the rectangle = 2(3x - 9 + x)
The Perimeter of the rectangle = 2(4x-9)
6x = 8x - 18
- 2x = - 18
x = 18/2
x = 9
Thus, the width = x = 9 ft
the length = 3x - 9 = 3(9) - 9
the length = 27 - 9
the length = 18 ft
Area = L × W
Area = (18 × 9)ft
Area = 162 sq. ft.
Cost of a Tile = $1.69 per sq. ft.
Thus;
Total Cost of tile = $1.69 × 162
Total Cost of tile = $273.28
Answer:
$273.78
Step-by-step explanation:
the other guy is wrong my dude
ou and a friend are heading to the movies. You each buy a ticket and you also want to buy some refreshments. The total cost of admission per person, a, is $7.50 and you spent $15.50 on refreshments. Write an expression to represent the total cost of the trip. Then, find the total cost.
Answers
Answer:
Expression: $7.50x + 15.50 = y Total Cost: $30.50
Step-by-step explanation:
x goes next to 7.50 because it is 7.50 per person, which makes it a variable that varies and can change.
since the expression is $7.50x + 15.50 = y, we just plug x in for 2 because he and his friend are going which is 2 people.
7.50(2) + 15.50 = 30.50
Lisa is building a structure to be used in the school play. The structure is in the shape of a right
triangular prism. A sketch is shown.
Lisa will paint the outside of the entire structure after building it. What is the area Lisa will paint? Be
sure to include the units label.
Lisa will paint an area of_____
Answers
The required Lisa will paint an area of 350.4 square feet.
To calculate the area that Lisa will paint, we need to find the total surface area of the right triangular prism. The total surface area includes the area of the two triangular bases and the three rectangular faces.
The area of a triangle can be calculated using the formula: Area = (1/2) * base * height.
Given that the base of the triangle is 8 feet and the height is 6 feet, we can calculate the area of one triangular base as follows:
Area of one triangular base = (1/2) * 8 ft * 6 ft = 24 ft²
Since there are two triangular bases, the total area of the triangular bases is:
The total area of triangular bases = 2 * 24 ft² = 48 ft²
The total area of the 3 rectangular faces is given as:
= 12.6[8+6+10]
= 302.4 ft²
To find the total surface area, we add the areas of the triangular bases and the rectangular faces:
Total surface area = Total area of triangular bases + Total area of rectangular faces
Total surface area = 302.4 ft² + 48 ft² = 350.4 ft²
Therefore, Lisa will paint an area of 350.4 square feet.
Learn more about the surface area here:
https://brainly.com/question/29298005
#SPJ4

2-1, An incompressible fluid is flowing at steady state in the annular region (i.e., torus or ring between two concentric cylinders). The coaxial cylinders have an outside radius of R and inner radius of a R. Find: (a) Shear stress profile (b) Velocity profile (c) Maximum and average velocities 2-2. Repeat problem 2-1 for flow between very wide or broad parallel plates separated by a distance 2h.
Answers
2-1. a) The shear stress τ is constant across the flow. b) The velocity is maximum at the center (r = 0) and decreases linearly as the radial distance increases. c)v_max = (P₁ - P₂) / (4μL) * \(R^{2}\) and v_avg = (1 / (π(\(R^{2} -a^{2}\)))) * ∫[a to R] v * 2πr dr 2-2.a) The shear stress is constant for parallel plates. b) The velocity profile shows that the velocity is maximum at the centerline and decreases parabolically .c)v_max = (P₁ - P₂) / (2μh) and v_avg = (1 / (2h)) * ∫[-h to h] v dr.
2-1. Flow in an annular region between concentric cylinders:
(a) Shear stress profile:
In an incompressible fluid flow between concentric cylinders, the shear stress τ varies with radial distance r. The shear stress profile can be obtained using the Navier-Stokes equation:
τ = μ(dv/dr)
where τ is the shear stress, μ is the dynamic viscosity, v is the velocity of the fluid, and r is the radial distance.
Since the flow is at steady state, the velocity profile is independent of time. Therefore, dv/dr = 0, and the shear stress τ is constant across the flow.
(b) Velocity profile:
To determine the velocity profile in the annular region, we can use the Hagen-Poiseuille equation for flow between concentric cylinders:
v = (P₁ - P₂) / (4μL) * (\(R^{2} -r^{2}\))
where v is the velocity of the fluid, P₁ and P₂ are the pressures at the outer and inner cylinders respectively, μ is the dynamic viscosity, L is the length of the cylinders, R is the outer radius, and r is the radial distance.
The velocity profile shows that the velocity is maximum at the center (r = 0) and decreases linearly as the radial distance increases, reaching zero at the outer cylinder (r = R).
(c) Maximum and average velocities:
The maximum velocity occurs at the center (r = 0) and is given by:
v_max = (P₁ - P₂) / (4μL) * \(R^{2}\)
The average velocity can be obtained by integrating the velocity profile and dividing by the cross-sectional area:
v_avg = (1 / (π(\(R^{2} -a^{2}\)))) * ∫[a to R] v * 2πr dr
where a is the inner radius of the annular region.
2-2. The flow between parallel plates:
(a) Shear stress profile:
For flow between very wide or broad parallel plates, the shear stress profile can be obtained using the Navier-Stokes equation as mentioned in problem 2-1. The shear stress τ is constant across the flow.
(b) Velocity profile:
The velocity profile for flow between parallel plates can be obtained using the Hagen-Poiseuille equation, modified for this geometry:
v = (P₁ - P₂) / (2μh) * (1 - (\(r^{2} /h^{2}\)))
where v is the velocity of the fluid, P₁ and P₂ are the pressures at the top and bottom plates respectively, μ is the dynamic viscosity, h is the distance between the plates, and r is the radial distance from the centerline.
The velocity profile shows that the velocity is maximum at the centerline (r = 0) and decreases parabolically as the radial distance increases, reaching zero at the plates (r = ±h).
(c) Maximum and average velocities:
The maximum velocity occurs at the centerline (r = 0) and is given by:
v_max = (P₁ - P₂) / (2μh)
The average velocity can be obtained by integrating the velocity profile and dividing by the distance between the plates:
v_avg = (1 / (2h)) * ∫[-h to h] v dr
These formulas can be used to calculate the shear stress profile, velocity profile, and maximum/average velocities for the given geometries.
Learn more about shear stress;
https://brainly.com/question/30407832
#SPJ4
Please answer 4 and 5 Thanks

Answers
Answer:
3. = C. , 4 = C.
Step-by-step explanation:
If you mean 3 and 4:
The trees extended high in the sky is not figurative language. It is simply stating that the trees are tall.
A Metaphor compares two things without using like or as. A simile compares two things using like or as. Giving human traits to an object is personification. And using an object or character to represent is a symbol, I believe.
Also, 2 is wrong. 2 should be B, as stated in the earlier paragraph.
Find a polar equation for the curve represented by the given Cartesian equation. x2+y2=25. x2+y2=−8y. y=√3x
Answers
The polar equation for this curve is: theta = pi/3 (or any angle that satisfies tan(theta) = sqrt(3))
To find the polar equation for the curve represented by the given Cartesian equations, we can use the conversion formulas between Cartesian and polar coordinates.
\(x^2 + y^2 = 25:\)
In polar coordinates, the conversion formulas are:
x = r cos(theta)
y = r sin(theta)
Substituting these values into the equation \(x^2 + y^2 = 25:\)
\((r cos(theta))^2 + (r sin(theta))^2 = 25\)
\(r^2 (cos^2(theta) + sin^2(theta)) = 25\)
\(r^2 = 25\)
The polar equation for this curve is simply:
r = 5
\(x^2 + y^2 = -8y:\)
In polar coordinates:
x = r cos(theta)
y = r sin(theta)
Substituting these values into the equation \(x^2 + y^2 = -8y:\)
\((r cos(theta))^2 + (r sin(theta))^2 = -8(r sin(theta))\)
\(r^2 (cos^2(theta) + sin^2(theta)) = -8r sin(theta)\)
\(r^2 = -8r sin(theta)\)
The polar equation for this curve is:
r = -8 sin(theta)
y = sqrt(3) x:
In polar coordinates:
x = r cos(theta)
y = r sin(theta)
Substituting these values into the equation y = sqrt(3) x:
r sin(theta) = sqrt(3) (r cos(theta))
r sin(theta) = sqrt(3) r cos(theta)
tan(theta) = sqrt(3)
The polar equation for this curve is:
theta = pi/3 (or any angle that satisfies tan(theta) = sqrt(3))
Learn more about polar equation here:
https://brainly.com/question/28847870
#SPJ11
MATH HELP ASAP! MARKING BRAINLIEST

Answers
((Ignore this)) (NOT y=3x+9)
Answer:
The correct answer is y = 3x + 3.
Step-by-step explanation:
take a look at my work.
sorry if my drawing is a little bit messy lol
On the graph you are rising up 3 units and running to the right 1 unit. According to rise over run, your rise is 3 and your run is 1. If you put that together that makes 3 over 1 or 3/1. Now when you simplify 3/1 you will get 3. You can simplify it by dividing 3/1 on your calculator or mentally which ever one is best for you. :)

How can you graph y= -2x + 5
Answers
Answer:
on desmos
Step-by-step explanation:
Solve 2x 10 = -4
X = ?
Answers
2x • 10 = -4
20x = -4
x = - 4/20 = -0.2
Answer: x = -0.2