When playing a game Emily had six more properties than Terry together they owned at least twenty of the properties. What is the smallest number of properties that Terry had
Answers
The smallest number of properties that Terry could have had is 7 properties.
Let's assume that Terry had x properties. Then, we know that Emily had x + 6 properties. Together, they owned at least 20 properties,
so:x + (x + 6) ≥ 20
2x + 6 ≥ 20
2x ≥ 14
x ≥ 7
Hence, Terry must have had at least 7 properties.
To understand why, we can think of it this way: if Terry had fewer than 7 properties, then Emily would have had even fewer than Terry (since she has 6 fewer properties than him).
If their combined total is at least 20, and Emily has fewer than Terry, then there's no way they could have reached a total of 20 or more properties.
Learn more about smallest number here:
https://brainly.com/question/29121232
#SPJ4
Related Questions
Please help me !! I need help ASAP

Answers
Answer:
1/5
Step-by-step explanation:
Which situation can be represented by the equation y = 25x + 50?
A. A repairman charges $25 to come to the house and $50 for each hour he works.
B. Tom pays $25 a month for a health club membership. He also had to pay a $50 registration fee.
C. Sally has $25 in her savings account. She plans on depositing $50 from each of her paychecks into her account.
D. A school store started the year with 25 pencils. Each month they added 50 more to their inventory.
Answers
Which of these is a correct step in constructing congruent angles?
A. Use a straightedge and draw an arc across the first arc from a leg of the given angle
B. Use a straightedge to measure the width between the points where the first arc cuts both legs of the given angle
C. Use a compass and draw an arc across both the legs of the given angle
D. Use a compass and join points to make the new leg of the congruent angle
Answers
Answer:
C. Use a compass and draw an arc across both the legs of the given angle.
Step-by-step explanation:
The value of k for which x²-4kxy+4y²=0 represent a pair of straight is?
Answers
Answer:
as the situation shows the formula
\((a + b) ^{2} \)
so the value of K is 1
2d – g³ = Ah
find A please:))
Answers
Answer:
\(A=\frac{2d-g^3}{h}\)
read the picture plsssssssssss

Answers
2. 2x - 5(3x^2)
3. 8x + 2x/3 +6
4. x + 3 - y - 6
Which problem is the same as 4 + 5
Answers
Answer:
6+3
Step-by-step explanation:
In a right triangle, the length of the hypotenuseis 14 cm and the length of one leg is 8 cm.What is the measure of the other leg?
Answers
Since it is a right triangle, we can use the Pythagorean Theorem. This one states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse. In algebraic notation:
\(\begin{gathered} a^2+b^2=c^2 \\ \text{ Where a and b are the legs and c is the hypotenuse of the right triangle.} \end{gathered}\)So, in this case, we have:
\(\begin{gathered} a=8\operatorname{cm} \\ b=? \\ c=14\operatorname{cm} \end{gathered}\)\(\begin{gathered} a^2+b^2=c^2 \\ (8cm)^2+b^2=(14cm)^2 \\ (8)^2cm^2+b^2=(14)^2cm^2 \\ 64cm^2+b^2=196cm^2 \\ \text{ Subtract }64cm^2\text{ from both sides of the equation} \\ 64cm^2+b^2-64cm^2=196cm^2-64cm^2 \\ b^2=132cm^2 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt{b^2}=\sqrt{132cm^2} \\ \boldsymbol{b}\approx\boldsymbol{11.49\operatorname{cm}} \end{gathered}\)Therefore, the measure of the other leg rounded to the nearest hundredth is 11.49 centimeters.

A bag contains 2
2
blue marbles, 2
2
red marbles, and 2
2
yellow marbles.
If Jenna randomly draws a marble from the bag (and puts it back) 15
15
times, how many times should she expect to pull a yellow marble?
Answers
Answer:
5 times
Step-by-step explanation:
Jenna wil most likely pull a yellow marble 1/3 of the time, because the total number of marbles is 6, and there are 2 yellow marbles, 2/6 which is 1/3. 1/3 times 15 is 5. So Jenna will most likely pull a yellow marble 5 times.
In a control chart application, we have found that the grand average over all the past samples of 6 units is X-Double Bar = 25 and R-Bar = 5.
a) Set up X-bar and R Control charts.
A2= 483 D3=0 D4=2.004
.483*5=2.415+25=27.415=UCL
.485*5=25-2.415=22.585=LCL
LCL(R bar)=0
UCL=10.020
b) The following measurements are taken from a new sample: 33, 37, 25, 35, 34 and 32. Is the process still in control?
Answers
Based on the given data, the process is out of control.
To determine if the process is still in control, we need to compare the new sample measurements to the control limits established in the X-bar and R control charts.
For the X-bar chart:
The UCL (Upper Control Limit) is calculated as the grand average (X-Double Bar) plus A2 times R-Bar:
UCL = 25 + (0.483 * 5) = 27.415
The LCL (Lower Control Limit) is calculated as the grand average (X-Double Bar) minus A2 times R-Bar:
LCL = 25 - (0.483 * 5) = 22.585
For the R chart:
The UCL (Upper Control Limit) for the R chart is calculated as D4 times R-Bar:
UCL = 2.004 * 5 = 10.020
The LCL (Lower Control Limit) for the R chart is 0.
Given the new sample measurements: 33, 37, 25, 35, 34, and 32, we can determine if any of the measurements fall outside the control limits. If any data point falls outside the control limits, it indicates that the process is out of control.
Upon comparing the new sample measurements to the control limits, we find that the measurement 37 exceeds the UCL of the X-bar chart. Therefore, the process is considered out of control.
Learn more about Limit here:
https://brainly.com/question/12211820
#SPJ11
Kelly bought a computer that was 20% off the regular price of $1,060. If a 7% sales tax was added to the cost of the computer, what was the total price Kelly paid for it?
Answers
Answer: $ 1361.04
Step-by-step explanation:
Discount will be 1060 * 20% = 212
Sales price 1060 + 212 = 1272
Tax 7% = 89.04
Kelly paid 1272 + 89.04 = 1361.04
NEED HELP THANK YOU !!
What is the distance of coordinates (8,4)(-3,4)?
Answers
Answer:
Mark them in a gtaph paper.
Step-by-step explanation:
Tke a graph paper and draw the x and y axis in the middle of the graph.
If u hv learned coordinates mark the points and count the boxes in between.
That will be ur answer
Thank me later
Complete the table and predict the limit, if it exists. (Round your answers to three decimal places. If the limit is infinite, enter '[infinity]' or '-[infinity]', as appropriate. If the limit does not otherwise exist, enter DNE.)
f(x) = 63 − 2x − x2 x − 7 x f(x) 6.9 6.99 6.999 7.001 7.01 7.1 lim x→7 f(x) =
Answers
The required limit of f(x) as x approaches 7 is -2.
The given table and the limit can be completed as shown below:\(x 6.9 6.99 6.999 7.001 7.01 7.1f(x) 61.61 60.8393 60.8039 60.8041 60.8389 61.61limit x → 7 f(x) = [latex]\color{blue}\text{-2}[/latex].\)
In the given problem, we need to complete the table and predict the limit if it exists.
First, let's plug in the values of x into the given function \(f(x) = 63 - 2x - x²/x - 7\) and fill the table as shown:x\(f(x)6.9 61.616.99 60.83936.999 60.80397.001 60.80417.01 60.83897.1 61.61\)
Now, we need to determine the limit of f(x) as x approaches 7.
To find the limit of f(x) as x approaches 7, we can either factor or use L'Hopital's rule.
Here, we will use factorization as shown below:\(f(x) = 63 - 2x - x²/x - 7= [(9 - x)(7 + x)]/[(x - 7)(1)] (x ≠ 7)\)
By canceling the common factor (x - 7) from the numerator and the denominator of the function f(x), we can simplify the function as shown:\(f(x) = -(x + 9) (x ≠ 7).\)
The limit of the function f(x) as x approaches 7 can now be calculated as follows\(:lim x → 7 f(x) = lim x → 7 -(x + 9) (x ≠ 7) = -(7 + 9) = -16\)
Thus, the limit of f(x) as x approaches 7 is -16.
Hence, the answer is -2. Therefore, the limit of f(x) as x approaches 7 is \([latex]\color{blue}\text{-2}[/latex].\)
Thus, the limit of f(x) as x approaches 7 is -2.
To know more about L'Hopital's rule visit:
brainly.com/question/24331899
#SPJ11
i need help with this for my little brother

Answers
Answer:
13
Step-by-step explanation:
it is hard
very unsure of this answer so pls help asap if you can!!

Answers
The following can be shown about the diagonals of parallelogram PQRS to compare the proof that diagonals of a parallelogram bisect each other: B. PR and SQ have the same midpoint.
What is a parallelogram?In Mathematics and Geometry, a parallelogram is a geometrical figure (shape) and it can be defined as a type of quadrilateral and two-dimensional geometrical figure that has two (2) equal and parallel opposite sides.
In order for any quadrilateral to be considered as a parallelogram, two pairs of its parallel opposite sides must be equal (congruent). This ultimately implies that, the diagonals of a parallelogram would bisect one another only when their midpoints are the same:
(Line segment PR)/2 = (Line segment SQ)/2
Line segment PR = Line segment SQ
Read more on a parallelogram here: brainly.com/question/31416609
#SPJ1
Pleas help, I’ll mark as brainliest.

Answers
Answer:
When f(x) is 0, then x is -1.8.
Step-by-step explanation:
To find this, you simply have to look for the place where the line crosses the x axis. This is where y (or f(x)) is equal to 0. Since this graph only crosses that axis at x = -1.8, that is the number we are looking for.
What value does the 2 represent in the number 0.826
Answers
Answer:
.02
Step-by-step explanation:
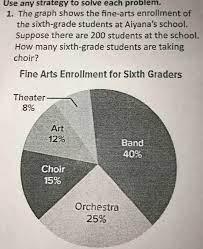
The graph shows the fine-arts enrollment of the sixth-grade students at Aiyana’s school. Suppose there are 200 students at the school. How many sixth-grade students are taking choir?
Answers
The number of sixth - grade students who are taking choir, given the graph on the fine-arts enrollment of the sixth-grade students at Aiyana’s school is 30 students .
How to find the number of students ?The number of students who are taking choir in the sixth - grade in Aiyana's school is :
= Percentage of students in the choir x Total enrollment of students
Percentage of students in the choir - 15 %
Total enrollment of students = 200 students
The students taking choir are therefore :
= 15 % x 200
= 30 students
Find out more on percentages at https://brainly.com/question/24304697
#SPJ1
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
The annual interest rate on a 15-year
mortgage on a house assessed at a value
Of $450 000 is 5 cents on every $1 What
is the interest paid on the mortgage for the
first year?
Answers
Answer:
The amount of interest paid is $22,500
Step-by-step explanation:
Firstly, we need the number of $1 in $450,000
That would simply be $450,000/$1 = 450,000
5 cents is same as 5/100 = $0.05
so we have to multiply 450,000 by 0.05
we have this as;
450,000 * $0.05 = $22,500
the amount of time it takes students to travel to school can vary greatly depending on how far a student lives from the school and what mode of transportation they take to school. a student claims that the average travel time to school for his large district is 20 minutes. to further investigate this claim, he selects a random sample of 50 students from the school and finds that their mean travel time is 22.4 minutes with a standard deviation of 5.9 minutes. he would like to conduct a significance test to determine if there is convincing evidence that the true mean travel time for all students who attend this school is greater than 20 minutes. what are the appropriate hypotheses?
Answers
Answer: The appropriate hypotheses for this significance test are:
Null hypothesis (H0): The true mean travel time for all students who attend this school is equal to 20 minutes.
Alternative hypothesis (Ha): The true mean travel time for all students who attend this school is greater than 20 minutes.
The null hypothesis states that there is no difference between the claim (20 minutes) and the sample mean (22.4 minutes). The alternative hypothesis states that there is a difference and the sample mean is greater than the claim. The student will use the sample data and a chosen significance level (such as α = 0.05) to decide whether to reject or fail to reject the null hypothesis.
Step-by-step explanation:
Find the solution to the system
of equations.
-4-3-2-1
432 H
1
7234
-21
-3
y x1-4
1234
X=4

Answers
The solution of the system of equations; \( y = \frac{1}{2}\cdot x - 1 \) and x = 4, represented on the graph is the point (4, 1)
Where on a graph is the solution of the equations of two straight lines on the graph?The graphs are straight line graphs that can be represented with linear functions.
The points on the graph with blue line are; (2, 0), (0, -1)
The slope, m, is therefore;
m = (0 - (-1))/(2 - 0) = 0.5
From the point, (2, 0), we have;
y = 0.5•(x - 2) = 0.5•x - 1
y = 0.5•x - 1...(1)
\( y = \frac{1}{2}\cdot x - 1 \)
The equation of the graph that is constructed with red line is x = 4...(2)
The solution is given by equation (1) when x = 4 as follows;
On the blue line, y = 0.5•x - 1On the red line, x = 4The solution satisfies both lines, and it is the point of intersection. At the solution, therefore;
y = 0.5•x - 1 and x = 4
Which gives;
y = 0.5 × 4 - 1 = 1
At the solution, x = 4, and y = 1, which gives the point, (4, 1)
Learn more about linear functions here:
https://brainly.com/question/15602982
#SPJ1
Which complex number has an absolute value of 5?
–3 + 4i
2 + 3i
7 – 2i
9 + 4
Answers
Answer:
Step-by-step explanation:
-3 + 4i
value = square( (-3)^2 + (4i)^2 ) = sqr(9 + 16) = sqr(25) = 5
The absolute value is like the Pythagoras theorem
4.33
The number of internal disk drives (in millions) made at a plant in Taiwan during the past 5 years follows:
YEAR
DISK DRIVES
1
140
2
160
3
190
4
200
5
210
a)Forecast the number of disk drives to be made next year, using linear regression.
b)Compute the mean squared error (MSE) when using linear regression.
c)Compute the mean absolute percent error (MAPE).
Could some please help? I would like to make sure my caculations are correct.
Thank you
Answers
(a) Forecast: Linear regression the next year is approx 191.6007.
(b) MSE: Mean Squared Error is approximately 249.1585.
(c) MAPE: Mean Absolute Percent Error is approximately 10.42%.
(a) (a) Forecast using linear regression:
To forecast the number of disk drives for the next year, we can use linear regression to fit a line to the given data points. The linear regression equation is of the form y = mx + b, where y represents the number of disk drives and x represents the year.
Calculating the slope (m):
m = (Σ(xy) - n(Σx)(Σy)) / (Σ(x^2) - n(Σx)^2)
Σ(xy) = (1)(140) + (2)(160) + (3)(190) + (4)(200) + (5)(210) = 2820
Σ(x) = 1 + 2 + 3 + 4 + 5 = 15
Σ(y) = 140 + 160 + 190 + 200 + 210 = 900
Σ(x^2) = (1^2) + (2^2) + (3^2) + (4^2) + (5^2) = 55
m = (2820 - 5(15)(900)) / (55 - 5(15)^2)
m = (2820 - 6750) / (55 - 1125)
m = -3930 / -1070
m ≈ 3.6729
Calculating the y-intercept (b):
b = (Σy - m(Σx)) / n
b = (900 - 3.6729(15)) / 5
b = (900 - 55.0935) / 5
b ≈ 168.1813
Using the equation y = 3.6729x + 168.1813, where x represents the year, we can predict the number of disk drives for the next year. To do so, we substitute the value of x as the next year in the equation. Let's assume the next year is represented by x = 6:
y = 3.6729(6) + 168.1813
y ≈ 191.6007
Therefore, according to the linear regression model, the predicted number of disk drives for the next year is approximately 191.6007.
(b) Calculation of Mean Squared Error (MSE):
To calculate the Mean Squared Error (MSE), we need to compare the predicted values obtained from linear regression with the actual values given in the data.
First, we calculate the predicted values using the linear regression equation: y = 3.6729x + 168.1813, where x represents the year.
Predicted values:
Year 1: y = 3.6729(1) + 168.1813 = 171.8542
Year 2: y = 3.6729(2) + 168.1813 = 175.5271
Year 3: y = 3.6729(3) + 168.1813 = 179.2000
Year 4: y = 3.6729(4) + 168.1813 = 182.8729
Year 5: y = 3.6729(5) + 168.1813 = 186.5458
Next, we calculate the squared difference between the predicted and actual values, and then take the average:
MSE = (Σ(y - ŷ)^2) / n
MSE = ((140 - 171.8542)^2 + (160 - 175.5271)^2 + (190 - 179.2000)^2 + (200 - 182.8729)^2 + (210 - 186.5458)^2) / 5
MSE ≈ 249.1585
The Mean Squared Error (MSE) for the linear regression model is approximately 249.1585.
This value represents the average squared difference between the predicted values and the actual values, providing a measure of the accuracy of the model.
(c) Calculation of Mean Absolute Percent Error (MAPE):
To calculate the Mean Absolute Percent Error (MAPE), we need to compare the predicted values obtained from linear regression with the actual values given in the data.
First, we calculate the predicted values using the linear regression equation: y = 3.6729x + 168.1813, where x represents the year.
Predicted values:
Year 1: y = 3.6729(1) + 168.1813 ≈ 171.8542
Year 2: y = 3.6729(2) + 168.1813 ≈ 175.5271
Year 3: y = 3.6729(3) + 168.1813 ≈ 179.2000
Year 4: y = 3.6729(4) + 168.1813 ≈ 182.8729
Year 5: y = 3.6729(5) + 168.1813 ≈ 186.5458
Next, we calculate the absolute percent error for each year, which is the absolute difference between the predicted and actual values divided by the actual value, multiplied by 100:
Absolute Percent Error (APE):
Year 1: |(140 - 171.8542) / 140| * 100 ≈ 18.467
Year 2: |(160 - 175.5271) / 160| * 100 ≈ 9.704
Year 3: |(190 - 179.2000) / 190| * 100 ≈ 5.684
Year 4: |(200 - 182.8729) / 200| * 100 ≈ 8.563
Year 5: |(210 - 186.5458) / 210| * 100 ≈ 11.682
Finally, we calculate the average of the absolute percent errors:
MAPE = (APE₁ + APE₂ + APE₃ + APE₄ + APE₅) / n
MAPE ≈ (18.467 + 9.704 + 5.684 + 8.563 + 11.682) / 5 ≈ 10.42
The Mean Absolute Percent Error (MAPE) for the linear regression model is approximately 10.42%.
This value represents the average percentage difference between the predicted values and the actual values, providing a measure of the relative accuracy of the model.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ11
Hiliary made cake to celebrate her mom birthday each person in the family got 1/4 of the cake if she would cut in to 8 slice how much of the cake did she person get?
Answers
Given that,
Each person in the family got 1/4 of the cake.
Cake is cut in 8 slices.
To find,
How much of the cake did the person get?
Solution,
To find the cake the person get can be calculated by finding 1/4th of 8 slices. Let the result is x.
x = (1/4) 8
= 2 slices
Hence, the person will get 2 slices.
use the quadratic formula to solve x^2 + 3^x - 28 = 0
Answers
Step-by-step explanation:
x^2 + 3x - 28 = 0
x^2 - 7x + 4x - 28 = 0
x(x-7) + 4(x-7) = 0
(x+4)(x-7)= 0
x+4=0 or x-7=0
x= -4 or x=7
5. When does a within sample variance occur?
Select one:
a. Within a single sample or group
b. Only within groups
c. Within multiple samples or groups
d. Only within samples
6. When validating assumpt
Answers
Within sample variance occurs within a single sample or group.
Within sample variance refers to the variation or dispersion of values within a single sample or group. It measures how much the individual data points deviate from the mean or central tendency within that specific sample. This variance is calculated by taking the average of the squared differences between each data point and the sample mean.
For example, let's say we have a sample of test scores for a group of students. Within sample variance would help us understand how much the individual test scores vary within that particular group. If the test scores are tightly clustered around the mean, the within sample variance would be low, indicating a high level of similarity among the scores. Conversely, if the test scores are widely spread out, the within sample variance would be high, suggesting a greater diversity or variability among the scores.
In summary, within sample variance occurs within a single sample or group and quantifies the dispersion of values around the mean within that sample. It helps assess the level of variation or homogeneity within the data set.
Learn more about variance occurs
brainly.com/question/32432947
#SPJ11
If you were offered $50,000 for 30 days work or 1 penny doubled everyday for thirty days which would you take?
Answers
if they were to choose the 1 penny doubled every day for 30 days, they would earn a total of $5,368,709.12.
If given the choice between $50,000 for 30 days of work or 1 penny doubled every day for 30 days, the option to choose would depend on a variety of factors.
The first thing to consider is the total amount of money that would be earned. If one were to choose the $50,000 for 30 days of work, they would earn a flat rate of $50,000. However, if they were to choose the 1 penny doubled every day for 30 days, they would earn a total of $5,368,709.12.
The second factor to consider is the amount of time and effort required for each option. If one were to choose the $50,000 for 30 days of work, they would be required to work for 30 days, which could be a significant commitment of time and effort. On the other hand, if they were to choose the 1 penny doubled every day for 30 days, they would not have to work at all, but they would have to wait 30 days to receive their payment.
Another factor to consider is the potential risks involved. If one were to choose the $50,000 for 30 days of work, they would be guaranteed to receive that amount of money. However, if they were to choose the 1 penny doubled every day for 30 days, there would be some level of uncertainty involved. While it is mathematically certain that the amount of money would double each day, there is always the possibility of unforeseen circumstances that could impact the final payout.
In conclusion, the decision of whether to choose the $50,000 for 30days of work or 1 penny doubled every day for 30 days ultimately depends on personal preferences and circumstances. While the potential payout of the penny-doubling option is significantly higher, it also requires patience and carries a degree of risk
To know more about penny doubled click here:
brainly.com/question/11624641
#SPJ4
gabi and mina both okay a single player game where they try to survive as many rounds as possible without crashing their car into a wall here's the historical data for how many rounds

Answers
Answer:
It's exactly normal, because both populations are normally distributed.
Step-by-step explanation:
khan :)
Which expression is represented by the model

Answers
Answer:
D.
hope this helps
have a good day :)
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
There are 3 out of 8 shaded in the box, and there are two whole ones, making it:
2 × 3/8
----------------------------------------------------------------------------------------------------------------
Have a good day :)