What is X equal to if 1X+30=6X+20?
Answers
Answer:
x=2
Step-by-step explanation:
1*x+30=6x+20
Multiply 1*x=x
x+30=6x+20
Subtract 30 from both sides:
x+30-30=6x+20-30
Simplify:
x=6x-10
Subtract 6x from both sides
x-6x=6x-10-6x
Simplify:
-5x=-10
Divide both sides by -5
-5x/5=-10/-5
Answer:x=2
Related Questions
Blank hundreds is the same as 4 thousand
Answers
Given two independent random samples with the following results: n1=8x‾1=186s1=33 n2=7x‾2=171s2=23 Use this data to find the 90% confidence interval for the true difference between the population means. Assume that the population variances are equal and that the two populations are normally distributed. Step 1 of 3: Find the point estimate that should be used in constructing the confidence interval.
Answers
Answer:
The point of estimate for the true difference would be:
\( 186-171= 15\)
And the confidence interval is given by:
\( (186-171) -1.77 \sqrt{\frac{33^2}{8} +\frac{23^2}{7}}= -10.753\)
\( (186-171) +1.77 \sqrt{\frac{33^2}{8} +\frac{23^2}{7}}= 40.753\)
Step-by-step explanation:
For this case we have the following info given:
\( \bar X_1 = 186\) the sample mean for the first sample
\( \bar X_2 = 171\) the sample mean for the second sample
\(s_1 =33\) the sample deviation for the first sample
\(s_2 =23\) the sample deviation for the second sample
\(n_1 = 8\) the sample size for the first group
\(n_2 = 7\) the sample size for the second group
The confidence interval for the true difference is given by:
\( (\bar X_1 -\bar X_2) \pm t_{\alpha/2}\sqrt{\frac{s^2_1}{n_1} +\frac{s^2_2}{n_2}}\)
We can find the degrees of freedom are given:
\( df = n_1 +n_2 -2 =8+7-2= 13\)
The confidence level is given by 90% so then the significance would be \(\alpha=1-0.9=0.1\) and \(\alpha/2=0.05\) we can find the critical value with the degrees of freedom given and we got:
\( t_{\alpha/2}= \pm 1.77\)
The point of estimate for the true difference would be:
\( 186-171= 15\)
And replacing into the formula for the confidence interval we got:
\( (186-171) -1.77 \sqrt{\frac{33^2}{8} +\frac{23^2}{7}}= -10.753\)
\( (186-171) +1.77 \sqrt{\frac{33^2}{8} +\frac{23^2}{7}}= 40.753\)
For an aptitude test for quality-control technicians in an electronics firm, history shows scores to be normally distributed with a variance of 2500. For 20 applications who took the test, the sample standard deviation was 68. Is there enough evidence to reject the assumption that the variance of scores is 2500. Use significance level of 0.05.
Answers
Answer:
\(\chi^2 =\frac{20-1}{2500} 68^2 =35.14\)
The degrees of freedom are given by:
\( df = n-1=20-1=19\)
And the p value would be given by:
\(p_v =2*P(\chi^2 >35.14)=0.0268\)
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true variance for this case is different from 2500
Step-by-step explanation:
Information given
\(n=20\) represent the sample size
\(\alpha=0.05\) represent the confidence level
\(s^2 =68^2=4624 \) represent the sample variance obtained
\(\sigma^2_0 =2500\) represent the value that we want to test
Null and alternative hypothesis
We want to test if the true variance is 2500, so the system of hypothesis would be:
Null Hypothesis: \(\sigma^2 = 2500\)
Alternative hypothesis: \(\sigma^2 \neq 2500\)
Calculate the statistic
The statistic would be given by:
\(\chi^2 =\frac{n-1}{\sigma^2_0} s^2\)
Repalcing we got:
\(\chi^2 =\frac{20-1}{2500} 68^2 =35.14\)
The degrees of freedom are given by:
\( df = n-1=20-1=19\)
And the p value would be given by:
\(p_v =2*P(\chi^2 >35.14)=0.0268\)
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true variance for this case is different from 2500
A box contains 5 blue balls, 2 white balls and 3 black balls. A ball is chosen randomly. Find the probability that the chosen ball is not black.
Answers
Answer:
7/10 or 70%
Step-by-step explanation:
Add the number of each color of balls together to get the total
5 + 2 + 3 = 10
Add the number of all the balls that aren't black
5 + 2 = 7
Then divide how many balls that aren't black by the total. This gives us the probability the ball you choose is not black
7/10 = 0.7 or 70%
Question
If n(A) = 14, n(B) = 51, and n(An B) = 12, then what is n(A U B)?
Answers
The value of n(AUB) i.e. union of A and B is 53.
What are Intersections and Unions in Probablity?
The union of two sets results in a new set that contains all of the items from both sets. The union is abbreviated as A∪B or "A or B." The intersection of two sets yields a new set containing all of the members from both sets. The junction is denoted by the letters A∩B or "A and B."
Solution:
Given that,
n(A) = 14
n(B) = 51
n(A∩B) = 12
We know that thee formula is n(AUB) = n(A) + n(B) - n(A∩B)
Putting the values,
n(AUB) = 14 + 51 - 12 = 53
So, the answer for the value of n(AUB) = 53
To learn more about Intersections and Unions from the given link
https://brainly.com/question/28278437
#SPJ1
Is the slope of a linear demand curve positive or nega-
tive?
Answers
The slope of a linear demand curve is negative
The demand curve's negative slope indicates that there is an inverse link between price and demand.
It is true that the demand curve's negative slope indicates an inverse link between price and quantity desired. According to the demand curve, demand declines as prices increase and rises as prices decrease.
This statement is false since it only applies to Giffen products, where the demand curve has a positive slope and a direct correlation between price and quantity desired.
Because unit requests rise when prices decrease and decline when prices rise, the demand curve often slopes downward (i.e., is negative). Demand increases when prices are low, but demand decreases when prices are high.
Learn more about demand curve here
https://brainly.com/question/1139186
#SPJ9
The table shows the greatest distance, in yards, that Bruce hit with six different clubs. State these distances in feet. The ratio of yards to feet is 1: 3.
Answers
Answer:
Yds Ft
99 -> 297
120 -> 369
144 -> 432
162 -> 486
174 -> 522
192 -> 576
Step-by-step explanation:
GEOMETRY 100 POINTS
Find the length of BC

Answers
Answer:
x = 16
Step-by-step explanation:
Opposite sides are equal in a parallelogram
AD = BC
5x - 12 = 3x + 20
5x - 3x = 20 + 12
2x = 32
x = 32/2
x = 16
here is the question please help

Answers
Answer:
IJ = 13
Step-by-step explanation:
If two secant segments are drawn to a circle from an exterior point, then the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant segment and its external secant segment.
Given:
Secants: IJK and MLK Point of intersection: KSo JK · IJK = LK · MLK
If MK = 15 and ML = 9, then LK = 15 - 9 = 6
Given JK = 5
⇒ JK · IJK = LK · MLK
⇒ 5 · IJK = 6 · 15
⇒ 5 · IJK = 90
⇒ IJK = 90 ÷ 5 = 18
IJ = IJK - JK
⇒ IJ = 18 - 5 = 13
What is the product?
(-202+5)(502-65)
O-1004+17025-652
-1004+170452-652
0-1004-7029-682
0-1004 +1702S+682

Answers
9514 1404 393
Answer:
(a) -10d^4 +17d^2s -6s^2
Step-by-step explanation:
Use the distributive property to eliminate parentheses, then collect terms.
\((-2d^2+s)(5d^2-6s)=-2d^2(5d^2-6s)+s(5d^2-6s)\\\\=(-2d^2)(5d^2) +(-2d^2)(-6s)+s(5d^2)+s(-6s)\\\\=-10d^4+12d^2s+5d^2s-6s^2\\\\=\boxed{-10d^4+17d^2s-6s^2}\)

let's see who can solve this. pleseeee

Answers
The correlation coefficient between X and Y is Corr(X, Y) = 0.
To calculate the marginal distribution of X and Y, we need to integrate the joint probability density function (PDF) over the appropriate ranges.
a. Marginal distribution of X:
To find the marginal distribution of X, we integrate the joint PDF over the range of Y:
∫[0, 1] J(x, y) dy
Since the joint PDF is defined as J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1 and J(x, y) = 0 otherwise, the integral becomes:
∫[0, x] 1 dy = x, for 0 ≤ x ≤ 1
So, the marginal distribution of X is simply X(x) = x for 0 ≤ x ≤ 1.
b. Expectation of X:
The expectation (mean) of X can be calculated as the integral of x times the marginal PDF of X:
\(E(X) = ∫[0, 1] x * X(x) dx = ∫[0, 1] x^2 dx = [x^3/3] from 0 to 1 = 1/3\)
Therefore, the expectation of X is E(X) = 1/3.
c. Variance of X:
The variance of X can be calculated using the formula:
\(Var(X) = E(X^2) - (E(X))^2E(X^2) = ∫[0, 1] x^2 * X(x) dx = ∫[0, 1] x^3 dx = [x^4/4] from 0 to 1 = 1/4Var(X) = 1/4 - (1/3)^2 = 1/4 - 1/9 = 5/36\)
Therefore, the variance of X is Var(X) = 5/36.
d. Covariance of X and Y:
The covariance of X and Y can be calculated as:
Cov(X, Y) = E(XY) - E(X)E(Y)
Since the joint PDF J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1, the integral becomes:
\(E(XY) = ∫[0, 1] ∫[0, x] xy dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
\(E(X) = 1/3 (from part b)E(Y) = ∫[0, 1] ∫[0, x] y J(x, y) dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
Cov(X, Y) = 1/6 - (1/3)(1/6) = 0
Therefore, the covariance of X and Y is Cov(X, Y) = 0.
e. Correlation coefficient between X and Y:
The correlation coefficient can be calculated using the formula:
Corr(X, Y) = Cov(X, Y) / √(Var(X) * Var(Y))
Since the covariance of X and Y is 0, the correlation coefficient will also be 0.
Therefore, the correlation coefficient between X and Y is Corr(X, Y) = 0.
f. Conclusion based on the correlation coefficient:
The correlation coefficient of 0 indicates that there is no linear relationship between X and Y. In this case, the fraction of male runners (X) and the
for more such question on correlation visit
https://brainly.com/question/13879362
#SPJ8
10. Over the summer, Maria read 2 books per week, and Janet read 4 books per week. Prior to the summer, Maria had read 28 books, and Janet had read 16 books. After w weeks, they had each read the same number of books. Write an equation to represent this situation. Then, solve the equation. Need a equation and solution.
Answers
6 WEEKS
2x + 28 = 4x + 16
x = 6
HURRY!!!
What is the value of |243| + |−23| − |−16|?
Answers
Answer:
250
Step-by-step explanation:
everything u need is in the picture

A pharmacy has purchased 550 products over a period of 3 months. If their average inventory was 235 products in a 3 month period what was their inventory turnover rate for this period
Answers
Answer:
2.34
Step-by-step explanation:
A pharmacy purchased 550 products over a period of 3 months
The average inventory was 235 products during the period of 3 months
Therefore, the inventory turnover rate for this period can be calculated as follows
= 550/235
= 2.34
Hence the inventory turnover rate for this period is 2.34
Plzzzzz Answer this its some easy points, I'm legit just dumb.
Answer both questions.

Answers
Answer:
A) Each of the smaller donations is $20.
B) The larger donation is greater than the smaller donations by $15.
Step-by-step explanation:
4+4+7 is equal to 15, and divide 75 by 15 to get $5 per part. Multiply 4 by 5 to get $20 for a smaller donation, and 7 by 5 to get $35 for the larger donation. Hope this helped :)
Answer:
Smaller donations each cost $20
The bigger donation is $15 more than the smaller ones.
Step-by-step explanation:
Let 4x be defined as the amount of the smaller donation, and let 7x be defined as the larger amount of the donation. We can then set up an equation:
4x+4x+7x = 75
15x = 75
x = 5
We can now plugin 5 for x to solve for the smaller donation and the larger donation:
Smaller donation = 4*5 = 20
Bigger donation = 7*5 = 35
Now, to find how much greater the bigger donation is, we just subtract 35 from 20, which is 15.
I hope this helped.
Super Saver grocery carries a 128 ounce jug of iced tea. The nutrition label states that the jug serves 16 people. Which rate best represents the relationship between the number of ounces of iced tea and the number of servings? F. 8 ounces per serving G. 16 servings per ounce H. 128 ounces per serving J. 8 servings per ounce
Answers
Answer:
I am pretty sure it is J
Step-by-step explanation:
128 divided by 16 equals 8
Answer:
F
8 ounce per serving
Step-by-step explanation:
128 ounce jug of iced tea.
label says = serves 16 people
therefore, the number of ounces per serving = 128 ounce / 16 serving
= 8 ounce per serving
so the answer is option F
I NEED THIS DONE NOW I'VE BEEN ON IT ALL DAY

Answers
Q5 is 115. Hope this helps! :) ✨
I can't see the numbers on Q6 sorry :((
The chart below represents the steps in the process of a bill becoming a law. Use the chart to answer the following question.
The image represents the process of a bill becoming a law. It shows a set of parallel lines that merge, then split into two, and then merge again. Moving left to right, the top line has boxes labeled: A, C, E, G, and H. The bottom line has boxes labeled: B, D, F, and I. Boxes A and B, C and D, E and F, H and I, are paired. G is the only box on the top line without a corresponding box on the bottom line. Continuing to move from left to right, the two lines merge into one and have one box labeled J. Then the lines separate into two parallel lines again. The top line is labeled with box K and the bottom line is labeled with box L. The two parallel lines continue to the right where they again merge into one line, with an arrow pointing to a final box labeled M.
© 2011 FLVS
Which section of this chart represents the point where a bill is first debated in subcommittees?
A and B
H and I
C and D
K and L
Answers
Based on the description provided, the section of the chart that represents the point where a bill is first debated in subcommittees is: C and D
How to explain the informationIn the given chart, the parallel lines represent the progression of a bill through various stages in the legislative process. The boxes on the top line represent one set of actions or steps, while the boxes on the bottom line represent another set of actions or steps.
Moving from left to right on the chart, the boxes A and B are paired, representing a particular stage in the process. Similarly, the boxes C and D are paired, indicating another stage in the process.
In the context of the question, the stage where a bill is first debated in subcommittees is represented by the boxes C and D.
Learn more about chart on
https://brainly.com/question/25032284
#SPJ1
Raymond is designing a ceramic pot on a coordinate system where each unit corresponds to 1 millimeter. The neck of the
pot has edges with the shape of a hyperbola, where the asymptotes y = 2.75x and y = -2.75x are followed. If the closest
that any part of the neck edges comes to the center of the neck is 32 millimeters, write an equation for the hyperbola used
to model the edges.
Answers
9514 1404 393
Answer:
x^2/1024 -y^2/7744 = 1
Step-by-step explanation:
The parent hyperbola relation is ...
x^2 -y^2 = 1
This has asymptotes of y = ±x and x-intercepts of ±1.
For the given hyperbola, we want to scale x by a factor of 32, and y by a factor that is 2.75 times that, or 88. Then the equation could be written as ...
(x/32)^2 -(y/88)^2 = 1
More conventionally, the denominator is shown at full value:
x^2/1024 -y^2/7744 = 1

anwser it pls aaaaaaaassaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

Answers
Answer:
Step-by-step explanation:
Volume = Bh
Turn the shape so the trapezoid is on the bottom/base
h=18 for overall shape
B = area of base, trapezoid
B = 1/2 (b₁ + b₂) h
b₁ = 11
b₂ = 25
h = 24 for trapezoid
B = 1/2 (11 + 25)(24)
B = 432
V = Bh
V = (432)(18)
V= 7776 in³
suppose that you have a photograph and you want to crop it to cut off 2 inches from the right side of the picture and then resize it using various scale factors (for our purposes here we will focus on a scale factor of 1.5). the transition from the dimensions of the original photograph to the dimensions of any scaled version is a two-step process.
Answers
Yes, cropping a picture and then using a scale factor to resize it is a two-step process.
The image is first cropped by subtracting 2 inches from the right side, altering the image's proportions.
The image is then enlarged using a scale factor of 1.5, which increases the image's dimensions by 1.5.
The final measurements of the image would be its original measurements less 2 inches (for cropping), then multiplied by 1.5. (for the resizing).
It's vital to keep in mind that both picture cropping and image scaling change the size of the final product.
Yes, cropping a photo, then resizing it with a scale factor, is a two-step process.
To learn more about measurement, refer to the link:brainly.com/question/4725561
#SPJ4
Your money grows at a rate of 8% a year if you originally invest $2,000 what is the function that represents your money after t years
Answers
Answer:
2000*(1.08)^t where t is years after deposit
Step-by-step explanation:
4. let a be n n. (a) if a is any square matrix, show 1 2 pa at q is symmetric. (b) show 1 2 pa ? at q is skew-symmetric. (c) show a can always be written as the sum of a symmetric and skew-symmetric matrix
Answers
(a)1/2 * (a + a^T) is symmetric.
(b)1/2 * (a - a^T) is skew-symmetric.
(c)a = 1/2 * (a + a^T) + 1/2 * (a - a^T). The first term is symmetric, and the second is skew-symmetric.
(a) If a is any square matrix, then 1/2 * (a + a^T) is symmetric. To show this, we need to prove that it is equal to its transpose.
(a + a^T)^T = a^T + (a^T)^T = a + a^T
Therefore, 1/2 * (a + a^T) is symmetric.
(b) If a is any square matrix, then 1/2 * (a - a^T) is skew-symmetric. To show this, we need to prove that it equals the negative of its transpose.
(a - a^T)^T = a^T - (a^T)^T = a - a^T
Therefore, 1/2 * (a - a^T) is skew-symmetric.
(c) Any square matrix can always be written as the sum of a symmetric and skew-symmetric matrix.
a = 1/2 * (a + a^T) + 1/2 * (a - a^T)
The first term is symmetric, and the second term is skew-symmetric.
Learn more about symmetric and skew-symmetric matrices here:https://brainly.com/question/26184753
#SPJ4
Merge onto Highway 40 and drive 3/5
mile. Stop and pay the toll. Then
continue on Highway 40 for twice this.
distance. How much longer will you be
on Highway 40 after you pay the foll?
Answers
Distance traveled after toll payment is 1.2 miles on highway 40.
What is Distance ?The distance may be calculated using a curved route. Displacement measurements can only be made along straight lines. Distance is path-dependent, meaning it varies depending on the direction followed. Displacement simply depends on the body's beginning and ending positions; it is independent of the route.
Distance is the sum of an object's movements, regardless of direction. Distance may be defined as the amount of space an item has covered, regardless of its beginning or finishing position.
The size or extent of the displacement between two points is referred to as distance. Keep in mind that the distance between two points and the distance traveled between them are not the same. The entire length of the journey taken between two points is known as the distance traveled. Travel distance is not a vector.
Distance traveled before toll payment =3/5 miles on highway 40
Distance traveled after toll payment =2*3/5 = 6/5 =
1.2 miles on highway 40.
To learn more about Distance refer to :
https://brainly.com/question/14886925
#SPJ1
The box whisker plots below (sometimes called boxplots) summarize the noon temperatures for each city. Use the box-and-whisker plots to answer the questions.
(a) Which city had more noon temperatures above 76 °F?
(b) Which city had noon temperatures with a larger interquartile range (IQR)?
(c) Which city had a larger median noon temperature?
(d) Which city had the highest noon temperature?
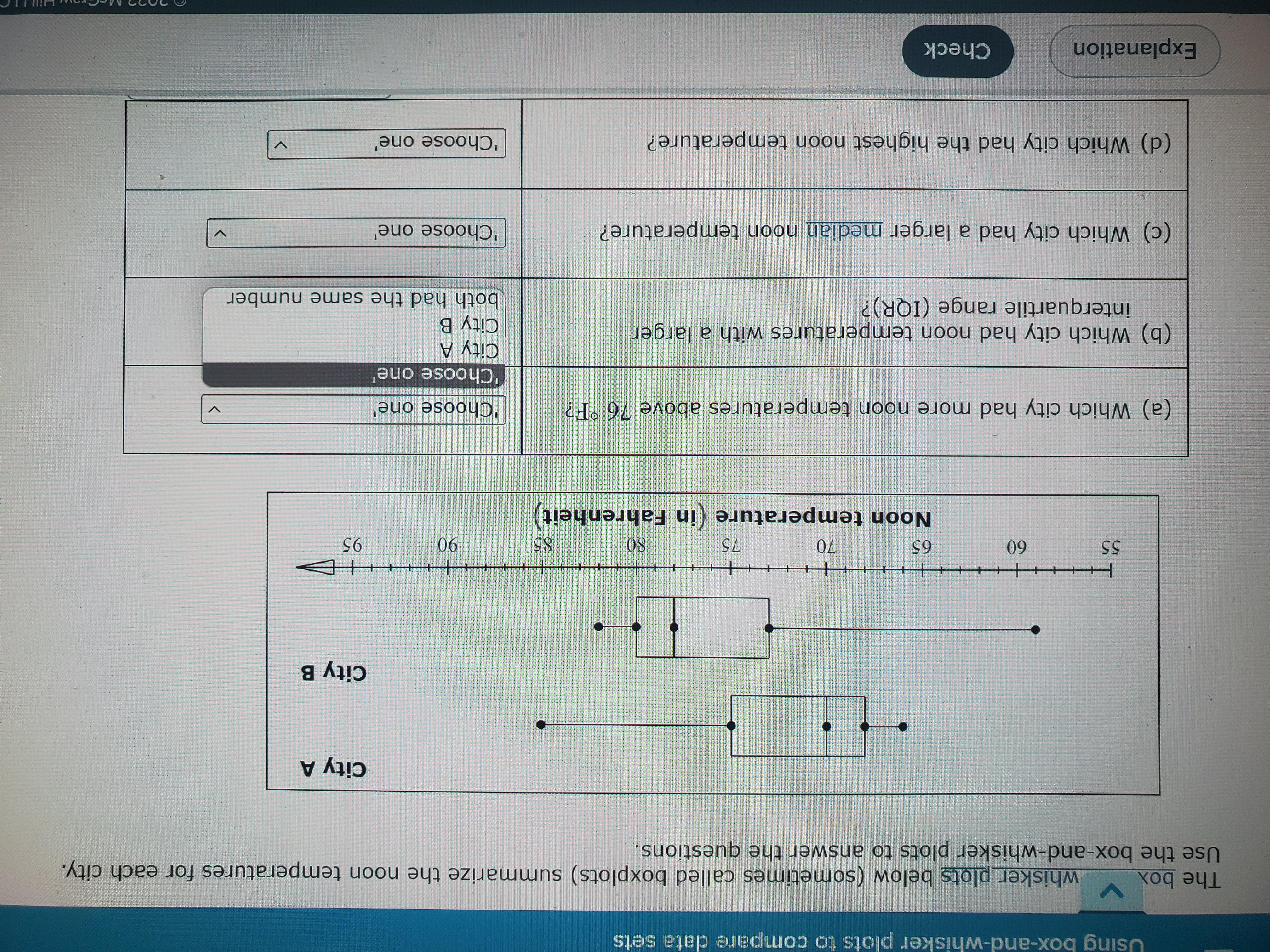
Answers
From the box-and-whisker plot, we have that:
a) City B had more noon temperatures above 76ºF.
b) City A had the largest IQR.
c) City B had the larger median temperature.
d) City A had the highest noon temperature.
What is shown by the box-and-whisker plots?For City A, the measures are given as follows:
Minimum temperature: 65ºF.First quartile: 67 ºF.Median: 70 ºF.Third quartile: 75 ºF.Highest temperature: 85ºF.Hence the interquartile range of temperatures is of:
75 - 67 = 8ºF.
For City B, the measures are given as follows:
Minimum temperature: 59ºF.First quartile: 73 ºF.Median: 78 ºF.Third quartile: 80 ºF.Highest temperature: 82ºF.Hence the interquartile range of temperatures is of:
80 - 73 = 7ºF.
More can be learned about box-and-whisker plots at https://brainly.com/question/3473797
#SPJ1
Determine the values of the parameter s for which the system has a unique solution, and describe the solution. x 1 - 5 sx 2
Answers
Answer:
\(s \ne \±2\)
\(x_1 = \frac{3s - 2}{3(s^2 -4)}\)
\(x_2 = \frac{2(s- 6)}{5(s^2 - 4)}\)
Step-by-step explanation:
Given
\(3sx_1 +5x_2 = 3\)
\(12x_1 + 5sx_2 =2\)
Required
Determine the value of s
Express the equations as a matrix
\(A =\left[\begin{array}{cc}3s&5\\12&5s\end{array}\right]\)
Calculate the determinant
\(|A|= (3s*5s -5 *12)\)
\(|A|= (15s^2 -60)\)
Factorize
\(|A|= 15(s^2 -4)\)
Apply difference of two squares
\(|A|= 15(s -2)(s + 2)\)
For the system to have a unique solution;
\(|A| =0\)
So, we have:
\(15(s -2)(s+2) = 0\)
Divide both sides by 15
\((s -2)(s+2) = 0\)
Solve for s
\(s -2 = 0\ or\ s +2 = 0\)
\(s = 2\ or\ s = -2\)
The result can be combined as:
\(s =\±2\)
Hence, the system has a unique solution when \(s \ne \±2\)
Next, we solve for s using Cramer's rule.
We have:
\(mat\ x_1 = \left[\begin{array}{cc}3&5\\2&5s\end{array}\right]\)
Calculate the determinant
\(|x_1| = (3 * 5s - 5 *2)\)
\(|x_1| = 15s - 10\)
So:
\(x_1 =\frac{|x_1|}{|A|}\)
\(x_1 = \frac{15s - 10}{15(s -2)(s+2)}\)
Factorize
\(x_1 = \frac{5(3s - 2)}{15(s -2)(s+2)}\)
Divide by 5
\(x_1 = \frac{3s - 2}{3(s -2)(s+2)}\)
\(x_1 = \frac{3s - 2}{3(s^2 -4)}\)
Similarly:
\(mat\ x_2 =\left[\begin{array}{cc}3s&3\\12&2\end{array}\right]\)
Calculate the determinant
\(|x_2| = 3s * 2 - 3 * 12\)
\(|x_2| = 6s- 36\)
So:
\(x_2 =\frac{|x_2|}{|A|}\)
\(x_2 = \frac{6s- 36}{15(s -2)(s+2)}\)
Factorize
\(x_2 = \frac{6(s- 6)}{15(s -2)(s+2)}\)
Divide by 3
\(x_2 = \frac{2(s- 6)}{5(s -2)(s+2)}\)
\(x_2 = \frac{2(s- 6)}{5(s^2 - 4)}\)
Convert 291 dg to kg.
Answers
Answer:
Question:
Convert 291 dg to kg
Concept:
Using the conversion rate, we will have
\(1kg=10^4dg\)By applying the conversion rate above, we will have that
\(\begin{gathered} 1kg=10^4dg \\ xkg=291dg \\ cross\text{ multiply, we will have} \\ 1\times291=x\times10^4 \\ 291=10000x \\ divide\text{ both sides by 10000} \\ \frac{10000x}{10000}=\frac{291}{10000} \\ x=0.0291kg \end{gathered}\)Hence,
The final answer is
\(\Rightarrow0.0291kg\)A car is 170 inches a tuck is 8% longer how long is the truck
Answers
hope this helped
2xy=z-y solve for x
Answers
Answer:
\(x=\frac{z-y}{2y}\)
Step-by-step explanation:

Some neighbors knows that you have very good geometry skills and asks for your help on their deck project. They did alright on the level pieces but the railing for the steps has them stumped. Help your neighbors determine how much wood is necessary to frame the outside of the railing. The railing height needs to be between 34 inches and 38 inches. Provide your answer in 3 to 5 sentences.

Answers
The length of the wood necessary to frame the outside of the railing will be 48.167 inches.
What is a Pythagoras theorem?The Pythagoras theorem states that the sum of two squares equals the squared of the longest side.
The Pythagoras theorem formula is given as
H² = P² + B²
The length of the wood necessary to frame the outside of the railing will be given as,
l² = 32² + 36²
l² = 1,024 + 1,296
l² = 2,320
I = 48.167 inches
The length of the wood necessary to frame the outside of the railing will be 48.167 inches.
More about the Pythagoras theorem link is given below.
https://brainly.com/question/343682
#SPJ1