What is the probability of flipping at least one head? Round the answer to the nearhundredth of a percent.

Answers
At least 1 head means
1 H, 4 T
or
2 H, 3 T
or
3 H, 2 T
or
4 H, 1 T
or
5 H
We have to find each individual probabilty and add them. So, in probability notation:
P(1H,4T) + P(2H,3T) + P(3H,2T) + P(4H,1T) + P(5H)
Recall that probability of heads/tails in each flip is equal to 0.5
The flips are independent of each other. It doesn't matter what happened in 1 flip, it doesn't affect the next flip.
So,
P(1H,4T) = 0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.03125
All other probabilties are same, thus:
\(\begin{gathered} P\mleft(1H,4T\mright)+P\mleft(2H,3T\mright)+P\mleft(3H,2T\mright)+P\mleft(4H,1T\mright)+P\mleft(5H\mright) \\ =0.03125+0.03125+0.03125+0.03125+0.03125 \\ =0.15625 \end{gathered}\)In percentage:
0.15625 * 100 = 15.625%
Rounded to nearest hundredth,
15.63%Related Questions
are these proportional or no

Answers
Answer:
The 2nd box is the 1st box is not
Step-by-step explation:
it just is thi sway
Answer:
nooe!
Step-by-step explanation:
the first set ads up to 133/120 whike the second ads up to 2 so they aren't :)
16. -4x+3x=2
Please help

Answers
Answer:
x= -2
-------
7
Step-by-step explanation:
<1. combine like terms.>
<2.divide both sides of the equation by same terms.>
<3.Simplify.>: then Answer while come x= -2
------
7
In calculus, it can be shown that
e^x=infintesigmak=0 x^k/k!
We can approximate the value of for any x using the following sum e^x=infintesigmak=0 x^k/k!
a) Approximate e^2.2 n=3

Answers
Answer: \(7.39466666\)
Step-by-step explanation:
Setting \(x=2.2\) and \(n=3\),
\(e^{2.2} \approx \sum^{3}_{k=0} \frac{2.2^{k}}{k!}=\frac{2.2^0}{0!}+\frac{2.2^1}{1!}+\frac{2.2^2}{2!}+\frac{2.2^3}{3!} \approx 7.39466666\)
Answer:
7.39466667 (8 d.p.)
Step-by-step explanation:
We can approximate the value of eˣ for any x using the following sum formula:
\(\boxed{e^{x} \approx \displaystyle \sum^n_{k=0}\dfrac{x^k}{k!}}\)
To approximate \(e^{2.2}\) with n = 3, substitute x = 2.2 and n = 3 into the given sum formula:
\(e^{2.2} \approx \displaystyle \sum^3_{k=0}\dfrac{2.2^k}{k!}\)
To calculate the sum, substitute k with each value from 0 to 3 and add the results together:
\(\begin{aligned}e^{2.2} &\approx \displaystyle \sum^3_{k=0}\dfrac{2.2^k}{k!}\\\\&= \dfrac{2.2^0}{0!}+\dfrac{2.2^1}{1!}+\dfrac{2.2^2}{2!}+\dfrac{2.2^3}{3!}\\\\&= \dfrac{1}{1}+\dfrac{2.2}{1}+\dfrac{4.84}{2}+\dfrac{10.648}{6}\\\\&= 1+2.2+2.42+1.774666666...\\\\&=7.39466667\; \sf (8\;d.p.)\end{aligned}\)
Therefore, the approximate value of \(e^{2.2}\) is:
\(\large \textsf{$e^{2.2}$}=\boxed{7.39466667}\; \sf (8\;d.p.)}\)
Note: To obtain a more accurate approximate value, increase the value of n.
You model your investment account using the formula y = 20000(1.035)x where x represents the
number of years and y represents the account balance after x years. What is the growth rate of your
investment?
Answers
Answer:
Step-by-step explanation:
The growth rate of the investment is represented by the constant multiplier in the exponential term of the formula y = 20000(1.035)x. In this case, the constant multiplier is 1.035, which represents the annual growth rate of the investment account.
To calculate the growth rate as a percentage, we can subtract 1 from the constant multiplier, and then multiply the result by 100.
So, the growth rate of the investment is:
1.035 - 1 = 0.035
0.035 * 100 = 3.5%
Therefore, the growth rate of the investment is 3.5%.
The growth rate of the investment can be found by subtracting 1 from the base of the exponential function and converting the result to a percentage:
growth rate = (base - 1) x 100%
growth rate = (1.035 - 1) x 100%
growth rate = 0.035 x 100%
growth rate = 3.5%
Therefore, the growth rate of the investment is 3.5%.
Use the definition to calculate the derivative of the following function. Then find the values of the derivative as specified.

Answers
Answer:
Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.
Step-by-step explanation:
Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11
\(p(\theta)=\sqrt{11\theta}\)
\(\hrulefill\)
The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.
\(f'(x) = \lim_{{h \to 0}} \dfrac{{f(x+h) - f(x)}}{{h}}\)\(\hrulefill\)
To apply the definition of derivatives to this problem, follow these step-by-step instructions:
Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).
\(p(\theta)=\sqrt{11\theta}\)
Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:
\(p'(\theta) = \lim_{{h \to 0}} \dfrac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h}\)
Step 3: Take the limit:
We need to rationalize the numerator. Rewriting using radical rules.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h} \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11\theta + 11h} - \sqrt{11\theta} }{h}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h}\)
Now multiply by the conjugate.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h} \cdot \dfrac{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} } \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{(\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} )(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )} \\\\\\\)
\(\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11h}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\)
Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.
\(p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta+(0)} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\)
\(\therefore \boxed{\boxed{p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta} }}}\)
Thus, we have found the derivative on the function using the definition.
It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.\(\hrulefill\)
Now evaluating the function at the given points.
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}; \ p'(1)=??, \ p'(11)=??, \ p'(\frac{3}{11} )=??\)
When θ=1:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(1)= \dfrac{\sqrt{11} }{2\sqrt{1}}\\\\\\\therefore \boxed{\boxed{p'(1)= \dfrac{\sqrt{11} }{2}}}\)
When θ=11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(11)= \dfrac{\sqrt{11} }{2\sqrt{11}}\\\\\\\therefore \boxed{\boxed{p'(11)= \dfrac{1}{2}}}\)
When θ=3/11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(\frac{3}{11} )= \dfrac{\sqrt{11} }{2\sqrt{\frac{3}{11} }}\\\\\\\therefore \boxed{\boxed{p'(\frac{3}{11} )= \dfrac{11\sqrt{3} }{6}}}\)
Thus, all parts are solved.
Solve the following system of equation. Be sure to show each of your work steps.

Answers
The roots of given equation x^2 - 2x +3 are 1+4i , 1-4i
What is Quadratic Equation ?
Quadratic equation can be defined as the equation in which it is in the form of ax^2 + bx + c = 0
where c is a constant.
Given equations,
x^2 - 2x +3 = 0
so, we know that
the roots of a quadratic equation
= (- b + (√ b^2 - 4ac )) / 2a , (- b - (√ b^2 - 4ac )) / 2a
so,
here a = 1 b = -2 c = 3
by substituting the given values,
we get,
= 2+ (√ 4 - 4*1*3 ) / 2 , 2- (√ 4 - 4*1*3 ) / 2
= 2+ (√-8) / 2 , 2- (√-8) / 2
= 2+8i / 2 , 2-8i / 2
= 1 + 4i , 1- 4i
Hence, The roots of given equation x^2 - 2x +3 are 1+4i , 1-4i
To learn more about Quadratic equation from given link.
https://brainly.com/question/30098550
#SPJ1
1 + 16 = distance squared
Answers
Distance = √(17) Because 1 + 16 = 17
Find the approximate perimeter of rectangle ABCD plotted below.
A(-2,6)
B(3,3)
D(-8,-4)
C(-3,-7)

Answers
Answer:
35 units
Step-by-step explanation:
Perimeter of rectangle ABCD =2(L + W)
L = AD or BC (we only need to calculate one of the two)
W = AB or DC. (we only need to calculate one of the two).
Distance between A(-2, 6) and D(-8, -4):
\( AD = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Let,
\( A(-2, 6) = (x_1, y_1) \)
\( D(-8, -4) = (x_2, y_2) \)
\( AD = \sqrt{(-8 -(-2))^2 + (-4 - 6)^2} \)
\( AD = \sqrt{(-6)^2 + (-10)^2} \)
\( AD = \sqrt{36 + 100} = \sqrt{136} \)
\( AD = 11.7 \) (nearest tenth)
Distance between A(-2, 6) and B(3, 3):
\( AD = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Let,
\( A(-2, 6) = (x_1, y_1) \)
\( B(3, 3) = (x_2, y_2) \)
\( AB = \sqrt{(3 -(-2))^2 + (3 - 6)^2} \)
\( AB = \sqrt{(5)^2 + (-3)^2} \)
\( AB = \sqrt{25 + 9} = \sqrt{34} \)
\( AB = 5.8 \) (nearest tenth)
Perimeter of rectangle ABCD =2(AD + AB)
= 2(11.7 + 5.8)
= 2(17.5)
= 35 units
PLS HELP ASAP I NEED IT PLS


Answers
Step-by-step explanation:
The equation for this function is y=2x
So 32*2=64
36/2=18
2*x=2x
y/2=y/2
2x*2=4x
(x+3)*2=2x+6
Penelope is driving to college. She looks at a map to find out how far she has to drive. On the map, Penelope measures the distance to be 7.5 inches. If the map scale is 1.5 in. = 40 mi, how many miles does Penelope need to drive?
Please Help!!
Answers
Answer: 200 miles
Step-by-step explanation:
a=4, b=-2 and c=5, what is the value of 4b + 7a
Answers
Answer:
20
Step-by-step explanation:
the first step is plugging in -2 for b and 4 for a.
4(-2) + 7(4)
-8 + 28 = 20
give brainliest please!
hope this helps :)
The apparent midpoint of AB is –
Triangle ABC is placed on a grid as shown.
The apparent midpoint of AB is –
(1.5, 1.5)
(3, 3)
(4.5, 4.5)
(4.5, 1.5)
Answers
The apparent midpoint of AB is (3, 3) (option b).
To find the apparent midpoint of AB, we need to determine the coordinates that represent the midpoint of the line segment AB.
The given triangle ABC is placed on a grid. Since the coordinates are not provided for points A and B, we cannot directly calculate the midpoint using their coordinates. Therefore, we'll have to rely on the visual representation provided.
Looking at the grid, we can see that the line segment AB is a diagonal of the square formed by the grid lines. The square has sides of length 3 units, as it extends from (1, 1) to (4, 4).
The midpoint of a line segment is the point that divides the segment into two equal parts. Since the square has sides of length 3, the midpoint of AB should be at the halfway point between (1, 1) and (4, 4).
To calculate the coordinates of the midpoint, we take the average of the x-coordinates and the average of the y-coordinates.
The x-coordinate of the midpoint is (1 + 4) / 2 = 5 / 2 = 2.5.
The y-coordinate of the midpoint is (1 + 4) / 2 = 5 / 2 = 2.5.
Therefore, the apparent midpoint of AB is (2.5, 2.5).
However, none of the given options match the calculated midpoint. It's possible that there is an error or discrepancy in the given options. Based on the calculations, the correct apparent midpoint of AB should be (2.5, 2.5). Thus, the correct option is a.
For more such questions on midpoint, click on:
https://brainly.com/question/28443113
#SPJ8
FIRST ONE TO AWNSER CORRECTLY GETS BRAINLEIST-1.8 + (2.1) Show your work
Answers
Answer:
0.3
Step-by-step explanation:
2.1
-1.8
---------
0.3
Can someone please help me with this

Answers
Answer:
39 sq inches
Step-by-step explanation:
You need the area of the square base
Area = side^2
A = 3 x 3 = 9
And the 4 triangle sides.
Area of a triangle = 1/2(base)(height)
a = 1/2 (3)(5) = 7.5
We have 4 of those triangles on this shape
4 x 7.5 = 30
Add the triangles to the base for goal surface area
30 + 9 = 39 square inches
Based on a weather record, the probability of snowfall in a certain town in New York on January 1 is 0.230. Find the probability that next year there will be no snowfall in that town on January 1.
1. 0.770
2. 4.348
3. 0.299
4. 1.230
Answers
The probability that next year there will be no snowfall in that town on January 1 is,
P (no snowfall) = 0.770
The term probability refers to the likelihood of an event occurring. Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one.
We have to given that;
Based on a weather record, the probability of snowfall in a certain town in New York on January 1 is 0.230.
Now, WE get;
the probability that next year there will be no snowfall in that town on January 1 is,
P (no snowfall) = 1 - P (snowfall)
P (no snowfall) = 1 - 0.230
P (no snowfall) = 0.770
Thus, The probability that next year there will be no snowfall in that town on January 1 is,
P (no snowfall) = 0.770
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
Matt has two very active dogs named Theia and Odin who need to eat extra snacks to increase
their caloric intake. He uses math to figure out how much more to feed them. He tracks their
activity level to determine the increase.
The table below shows the number of treats per dog per week.
What is the average rate of change for the number of treats that Odin gets each week between
Week 1 and Week 5?
Week 2
Week 3
Week 5
Odin
Theia
Week 1
7
5
3
2.
00 00
Week 4
9
7
4
5
Week 6
5
6

Answers
Answer:
Step-by-step explanation:
That is cheating no help for you sorry
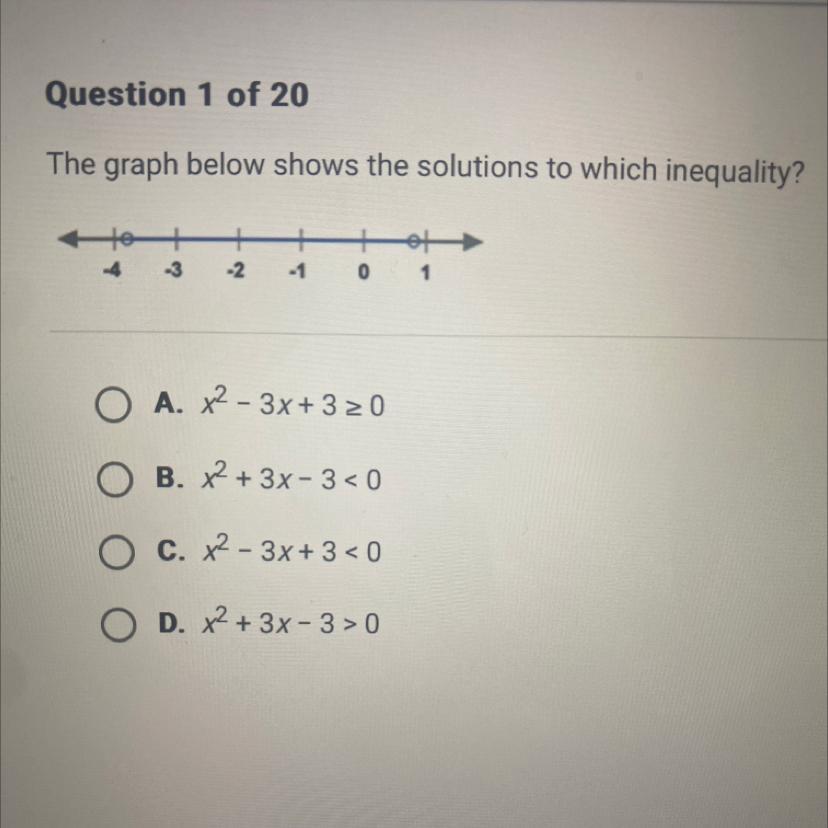
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
I have 17 ones, 15 tens, and 7 thousands
Answers
Answer:
You have 7,167
Step-by-step explanation:
If this was to be converted into a whole number, it would be:
7,167
5c+7y=13. Solve for y
Answers
Gf tj hyy u dfhgg he dghcdtcsrcdg
Answer:
1
Step-by-step explanation:
If C were to be 0, y would have to be 1 bc 7+5=12, and c is already zero, so you need 1 more, so y is 1
A 2-gallon container of disinfectant costs $20.48. What is the price per cup?
Answers
Answer:
$0.64 per cup
Step-by-step explanation:
There are 16 cups in 1 gallon, so the number of cups in 2 gallons is:
1 gallon: 16 cups
2 gallon = 2 x 1 gallon = 2 x 16 cups = 32 cups
So we need to find the price of each cup:
1 cup = ($20.48 / 32 cups) = $0.64 per cup.
Find the sum of the complex numbers (3+3i)+(8+7i)
Answers
Answer:
11 + 10i
Step-by-step explanation:
Just treat i like any other variable, and combine like terms. Hope that helps!
Which number is equal to four and five sixths?
A. four and eighty three hundredths with the three repeating
B. six twenty ninths C. 4.8 D. 484percent
Answers
The number that is equal to four and five sixths is A. four and eighty three hundredths with the three repeating
What is a fraction?A fraction is simply a piece of a whole. The number is represented mathematically as a quotient where the numerator and denominator are split. In a simple fraction, the numerator as well as the denominator are both integers.
The number that is equal to 4 5/6 will be illustrated thus:
= 4 5/6
= 4 + 0.8333.
= 4.8333
In this vase, the 3 is repeating. Therefore, the correct option is A.
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
Determine the total surface area and volume of each figure.

Answers
The total surface area of solid is,
S = 220 m²
And, The volume of the prism is, 200 m³
We have to given that;
A solid prism is shown in figure.
Since, The surface area of a prism is,
S = (2 × Base Area) + (Base perimeter × height)
Where, "S" is the surface area of the prism.
Hence, We get;
base area = 5 x 10 = 50 m²
height = 4 m
Base Perimeter = 2 (5 + 10) = 30
Hence, We get;
S = (2 x 50) + (30 x 4)
S = 100 + 120
S = 220 m²
Since, A prism is a solid shape that is bound on all its sides by plane faces. The volume of a prism is expressed as;
V = base area × height.
Now, For given figure,
Volume of the prism = base area × height
base area = 5 x 10 = 50 m²
height = 4 m
Hence, Volume = 50 × 4 m³
= 200 m³
Thus, The volume of the prism is, 200 m³
To learn more about the volume visit:
brainly.com/question/24372707
#SPJ1
The side length of an equilateral triangle is 20 centimeters. Find the length of altitude of the triangle.
Answers
Answer:
17.3 cm
Step-by-step explanation:
20² = 10² + x²
400 = 100 + x²
300 = x²
x = 17.3 cm
I need help on this one
Find the selling price.
Cost To Store: $50
Markup: 10%
The selling price is $blank

Answers
The selling price of the item at 10% marlkup is $55
Finding the selling price of the itemFrom the question, we have the following parameters that can be used in our computation:
Cost To Store: $50Markup: 10%Using the above as a guide, we have the following:
Selling price = Cost To Store * (1 + Markup)
substitute the known values in the above equation, so, we have the following representation
Selling price = 50 * (1 + 10%)
Evaluate
Selling price = 55
Hence the selling price of the item is $55
Read more about markup at
https://brainly.com/question/6500465
#SPJ1
An Olympic diver is competing for a metal. His height in meters above the water can be modeled by the function
f (x)= -4.9x^2+9.8x+14.7f(x)=−4.9x +9.8x+14.7
where is is the time in seconds after he begins the dive.
After how many seconds does he reach the water?
What domain makes sense for this scenario?
Answers
Answer:
-4.9x²+75x=-4.9x+50x+38
75x=50x+38
25x=38
x=1.52
1.52 -4.9(1.52)²+75(1.52)=102.67904≈102.7 meters
Double check: -4.9(1.52)²+50(1.52)+38=102.67904≈102.7. Yes.
102.7 meter.
Step-by-step explanation:
Mid-West Publishing Company publishes college textbooks. The company operates an 800 telephone number whereby potential adopters can ask questions about forthcoming texts, request examination copies of texts, and place orders. Currently, two extension lines are used, with two representatives handling the telephone inquiries. Calls occurring when both extension lines are being used receive a busy signal; no waiting is allowed. Each representative can accommodate an average of 15 calls per hour. The arrival rate is 30 calls per hour.
How many extension lines should be used if the company wants to handle 90% of the calls immediately?
fill in the blank 1
lines should be used
What is the average number of extension lines that will be busy if your recommendation in part (a) is used? Round your answer to four decimal places.
L = fill in the blank 2
What percentage of calls receive a busy signal for the current telephone system with two extension lines? Round your answer to two decimal places.
fill in the blank 3
%
Answers
The various answers to the question are:
To answer 90% of calls instantly, the organization needs four extension lines.The average number of extension lines that will be busy is FourFor the existing phone system with two extension lines, 34.25 % of calls get a busy signal.How many extension lines should be used if the company wants to handle 90% of the calls immediately?a)
A number of extension lines needed to accommodate $90 in calls immediately:
Use the calculation for busy k servers.
\($$P_{j}=\frac{\frac{\left(\frac{\lambda}{\mu}\right)^{j}}{j !}}{\sum_{i=0}^{k} \frac{\left(\frac{\lambda}{\mu}\right)^{t}}{i !}}$$\)
The probability that 2 servers are busy:
The likelihood that 2 servers will be busy may be calculated using the formula below.
\(P_{2}=\frac{\frac{\left(\frac{20}{12}\right)^{2}}{2 !}}{\sum_{i=0}^{2} \frac{\left(\frac{20}{12}\right)^{t}}{i !}}$$\approx 0.3425$\)
Hence, two lines are insufficient.
The probability that 3 servers are busy:
Assuming 3 lines, the likelihood that 3 servers are busy may be calculated using the formula below.
\(P_{j}=\frac{\frac{\left(\frac{\lambda}{\mu}\right)^{j}}{j !}}{\sum_{i=0}^{2} \frac{\left(\frac{\lambda}{\mu}\right)^{i}}{i !}}$ \\\\$P_{3}=\frac{\frac{\left(\frac{20}{12}\right)^{3}}{3 !}}{\sum_{i=0}^{3} \frac{\left(\frac{20}{12}\right)^{1}}{i !}}$$\approx 0.1598$\)
Thus, three lines are insufficient.
The probability that 4 servers are busy:
Assuming 4 lines, the likelihood that 4 of 4 servers are busy may be calculated using the formula below.
\(P_{j}=\frac{\frac{\left(\frac{\lambda}{\mu}\right)^{j}}{j !}}{\sum_{i=0}^{k} \frac{\left(\frac{\lambda}{\mu}\right)^{t}}{i !}}$ \\\\$P_{4}=\frac{\frac{\left(\frac{20}{12}\right)^{4}}{4 !}}{\sum_{i=0}^{4} \frac{\left(\frac{20}{12}\right)^{7}}{i !}}$\)
Generally, the equation for is mathematically given as
To answer 90% of calls instantly, the organization needs four extension lines.
b)
The probability that a call will receive a busy signal if four extensions lines are used is,
\(P_{4}=\frac{\left(\frac{20}{12}\right)^{4}}{\sum_{i=0}^{4} \frac{\left(\frac{20}{12}\right)^{1}}{i !}} $\approx 0.0624$\)
Therefore, the average number of extension lines that will be busy is Four
c)
In conclusion, the Percentage of busy calls for a phone system with two extensions:
The likelihood that 2 servers will be busy may be calculated using the formula below.
\(P_{j}=\frac{\left(\frac{\lambda}{\mu}\right)^{j}}{j !}$$\\\\$P_{2}=\frac{\left(\frac{20}{12}\right)^{2}}{\sum_{i=0}^{2 !} \frac{\left(\frac{20}{12}\right)^{t}}{i !}}$$\approx 0.3425$\)
For the existing phone system with two extension lines, 34.25 % of calls get a busy signal.
Read more about signal
https://brainly.com/question/14699772
#SPJ1
x-y=16
x-y=16
Solve using the substitution method
Answers
Step-by-step explanation:
x - y = 16 ---eq(1)
x - y = 16 ---eq(2)
From eq(1)
x - y = 16
x = 16 + y ---eq(3)
Substituting the value of eq(3) into eq(2)
(16 + y) - y = 16
16 = 16
We can't get a proper value for this pair of linear Equations
But, Since both the equations are the same, the lines formed by them will be coincident and therefore they will have infinitely many solutions
point(m,5)lies on the line given by the equation 5x-y=20.find m
Answers
Answer:
m = 5
Step-by-step explanation:
given point (m,5) lies on the line 5x-y=20,( x , y )
here x is m and y is 5, lets put it in the equation to solve:
5x-y=20
5(m) - 5 = 20
5m = 20 + 5
5m = 25
m = 25/5
m = 5
Based on the histogram, how many items cost less than $3.00 per pound?
here are the option I already eliminated one
A. 1
B. 3
C. 7

