What is the percent difference in si for an object located at so = 10f and so = [infinity]? what about so = 100f and so = [infinity]? when is it justified to consider an object to be located at ""optical infinity""?
Answers
The percent difference in si for an object located at so = 10f and so = [infinity] can be calculated using the formula:
Percent Difference = ((si - so) / so) * 100%
For so = 10f and so = [infinity], let's calculate the percent difference in si:
1. For so = 10f:
- Suppose the image distance si is 2f.
- Using the formula, the percent difference can be calculated as follows:
((2f - 10f) / 10f) * 100% = (-8f / 10f) * 100% = -80%
Therefore, the percent difference in si for an object located at so = 10f is -80%.
2. For so = [infinity]:
- When the object is located at "optical infinity" (so = [infinity]), the image distance si becomes equal to the focal length of the lens.
- If the lens is converging, the image distance si would be positive and equal to the focal length (si = f).
- If the lens is diverging, the image distance si would be negative and equal to the focal length (si = -f).
Therefore, when the object is located at "optical infinity," the image distance si will be equal to the focal length of the lens.
Now let's consider so = 100f and so = [infinity]:
1. For so = 100f:
- Suppose the image distance si is 2f.
- Using the formula, the percent difference can be calculated as follows:
((2f - 100f) / 100f) * 100% = (-98f / 100f) * 100% = -98%
Therefore, the percent difference in si for an object located at so = 100f is -98%.
2. For so = [infinity]:
- As mentioned earlier, when the object is located at "optical infinity" (so = [infinity]), the image distance si will be equal to the focal length of the lens.
So, the percent difference in si for an object located at so = [infinity] will always be 0%.
It is justified to consider an object to be located at "optical infinity" when the object is at a very far distance from the lens, where the rays of light can be approximated as parallel. In such cases, the image distance si becomes equal to the focal length of the lens, resulting in clear and focused images. This assumption simplifies calculations and analysis in optics.
percent difference and optical infinity : https://brainly.in/question/7995799
#SPJ11
Related Questions
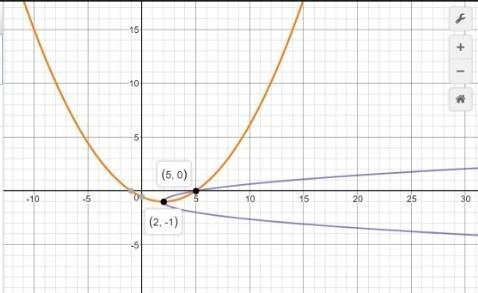
The vertex of this parabola is at 2, -1 When the y-value is 0 the x value is 5 what is the coefficient of the squared term in the parabola equation.
A. -3
B. -4
C. 4
D. 3
Answers
Answer:
\(\large \boxed{\sf \frac{1}{9}}\)
Step-by-step explanation:
\(\sf y=a(x-h)^2+k\)
\(\sf Vertex = (h,k)\)
y-value is 0 and the x value is 5
h = 2
k = -1
\(\sf 0=a(5-2)^2+-1\)
Solve for \(\sf a\) (the coefficient of the squared term).
\(\sf 0=a(3)^2+-1\)
\(\sf 0=9a-1\)
\(\sf 9a=1\)
\(\displaystyle \sf a=\frac{1}{9}\)
The coefficient of the squared term in the parabola equation is 1/9.
Answer:
Fot this parabola the coefficient for squared term is 7
Step-by-step explanation:
The formula for vertex equation is:
x = a*(y-h)^{2}+kx=a∗(y−h)
2
+k
if vertex is at (-3,-1) and in the formula the vertex is (k,h), we replace this values
x = a*(y +1)^{2} -3x=a∗(y+1)
2
−3
The other point of this parabola is (4,0), so we replace it in the formula below:
4 = a*(0 + 1)^{2} -34=a∗(0+1)
2
−3
4 = a*(1)-34=a∗(1)−3
4 +3= a*(1)4+3=a∗(1)
a=7a=7
Are the ratios 19:12 and 8:6 equivalent?
Answers
Answer:
no
Step-by-step explanation:
you basically divide or multiply something.
say you divide 2 for 8:6, divide 2 by both #s. 8:6 would then have the equivalent ratio of 4:3
hope it helps!
Help is needed please

Answers
Answer:
y = 0
Step-by-step explanation:
Let's use the addition method.
2x + y - 10 = 0
x - y - 5 = 0
Write the first equation as is. Write below it the second equation multiplied by -2 on both sides. Then add the equations.
2x + y - 10 = 0
(+) -2x + 2y + 10 = 0
--------------------------------
3y = 0
Divide both sides by 3.
y = 0
Answer: y = 0
How much does a 5 gallon of water weigh?
Answers
A 5-gallon container of water weighs approximately 41.7 pounds (18.9 kilograms). This is because water has a density of 1 kilogram per liter or 8.34 pounds per gallon. Therefore, a 5-gallon container holds 18.9 liters of water, which weighs 18.9 kilograms or 41.7 pounds.
A gallon of water is equivalent to 8.34 pounds of water. So 5-gallon of water is equivalent to
= 5 * 8.34
= 41.70
A gallon of water is equivalent to 3.78 litres of water. So 5-gallon of water is equivalent to
= 5 * 3.78
= 18.90
A litre of water is equivalent to 1 kilogram of water. So 18.90 litres of water is equivalent to
= 18.90 * 1
= 18.90
To know more on gallon
https://brainly.com/question/1462470
#SPJ4
the length and width of a rectangle are measured as 52 cm and 35 cm, respectively, with an error in measurement of at most 0.1 cm in each. use differentials to estimate the maximum error in the calculated area of the rectangle.
Answers
The maximum error in the calculated area of the rectangle is approximately 8.7 square centimeters.
To estimate the maximum error in the calculated area of the rectangle, we can use differentials. The formula for the area of a rectangle is A = length * width.
Given:
Length (L) = 52 cm (with a maximum error of 0.1 cm)
Width (W) = 35 cm (with a maximum error of 0.1 cm)
We want to find the maximum error in the calculated area (dA) when the length and width have a maximum error of 0.1 cm.
Using differentials, we have:
dA = (∂A/∂L) * dL + (∂A/∂W) * dW
Let's calculate the partial derivatives (∂A/∂L) and (∂A/∂W):
∂A/∂L = W (since the width is constant when differentiating with respect to L)
∂A/∂W = L (since the length is constant when differentiating with respect to W)
Substituting the values:
∂A/∂L = 35 cm
∂A/∂W = 52 cm
Now we can calculate the maximum error in the calculated area (dA) using the given maximum errors in length (dL) and width (dW):
dA = (35 cm * 0.1 cm) + (52 cm * 0.1 cm)
dA = 3.5 cm + 5.2 cm
dA = 8.7 cm
Therefore, the maximum error in the calculated area of the rectangle is approximately 8.7 square centimeters.
Learn more about rectangular from
https://brainly.com/question/2607596
#SPJ11
Based on the pattern, what are the next two terms of the sequence? 9, 15, 21, 27, . . .




Answers
Answer: 33,39
Step-by-step explanation:
Counting by 6's
Could someone do this question for me? Thanks

Answers
Answer:
20 counters/box
Step-by-step explanation:
Missing counters(m)= 8
Total number of counters available (t-m)= 132
Required number of counters(t):
=(t-m) + m
= 132 + 8 = 140
Total number of boxes(tB) = 7( 6 full and one with eight missing)
Total Counters/Boxes= t/tB
= 140/7
= 20
Could some one help me

Answers
Answer:
x=6.6 y=12
Step-by-step explanation:
To know this problem, you need to know the Pythagorean theorem, though I think you know this since it seems like you are doing a quiz or something like that. \(a^{2}\) + \(b^{2}\) = \(c^{2}\)
Solving x:Plug the numbers in\(8.8^{2}\)+\(x^{2}\)=\(11^{2}\)77.44+\(x^{2}\)=121121-77.44=43.56\(x^{2}\)=43.56\(\sqrt{x}\)=\(\sqrt{43.56}\)x=6.6Solving for y:Plug the numbers in\(6.6^{2} +10^{2} = y^{2}\)43.56+100=\(y^{2}\)143.56=\(y^{2}\)\(\sqrt{143.56} =\sqrt{y}\)12=yThis might be too late, but I hope you were able to do well on your thing!
[:
Which property should Remus use to solve the equation below? 7 q = 49 division property of equality addition property of equality subtraction property of equality identity property of equality.
Answers
Answer:
Division Property
Step-by-step explanation:
He needs to divide both sides by 7 to find the value of q
The division property of equality should Remus used to solve the given equation and this can be determined by using the given data.
Given :
Equation is \(7q = 49\).
The following steps can be used in order to determine the property that Remus use to solve the given equation:
Step 1 - Write the given equation.
\(7q = 49\)
Step 2 - The arithmetic operations can be used in order to evaluate the given equation.
Step 3 - Using the division property of equality the value of 'q' can be determined.
\(q = \dfrac{49}{7}\)
\(q = 7\)
Therefore, the correct option is A).
For more information, refer to the link given below:
https://brainly.com/question/11897796
Subtract 7b(2a 2 +5a-7) from (7a 2 -a+3 )-3b(6a 2 -b+3)
Answers
Answer:
\(\huge\boxed{-32a^2b+7a^2+3b^2-35ab-a+40b+3}\)
Step-by-step explanation:
\(7b(2a^2+5a-7)\qquad|\text{use the distributive property}\\\\=(7b)(2a^2)+(7b)(5a)+(7b)(-7)=14a^2b+35ab-49b\\\\\\(7a^2-a+3)-3b(6a^2-b+3)\qquad|\text{use the distributive property}\\\\=7a^2-a+3+(-3b)(6a^2)+(-3b)(-b)+(-3b)(3)\\\\=7a^2-a+3-18a^2b+3b^2-9b\)
Substraction
\((7a^2-a+3-18a^2b+3b^2-9b)-(14a^2b+35ab-49b)\\\\=7a^2-a+3-18a^2b+3b^2-9b-14a^2b-35ab+49b\\\\\text{combine like terms}\\\\=(-18a^2b-14a^2b)+7a^2+3b^2-35ab-a+(-9b+49b)+3\\\\=-32a^2b+7a^2+3b^2-35ab-a+40b+3\)
How do we draw graphs in those kinds of questions?

Answers
What is wrong in the following photo. Explain and justify your reasoning using key vocabulary words.

Answers
Answer:
91 degrees
Step-by-step explanation:
A right angle is 90 degrees, but in the photo it shows 91 degrees.
What is the value of s ?
Please help
No guessing

Answers
Answer:
s = 17Step-by-step explanation:
use Pythagorean theorem a² + b² = c²
where a = 8
b = 15
c = s (which is unknown)
plugin values into the formula:
a² + b² = c²
8² + 15² = s²
s = √(64 + 225)
s = √289
s = 17
help pls fhakahdksjhshdksj

Answers
Slope could also mean gradient, so the gradient of a line is always the number in front of x in the equation y=Mx+c ... Hope it was helpful:)
1000:311:29 in its simplest form
Answers
To simplify the ratio 1000:311:29, we need to find the greatest common factor (GCF) of the three numbers and divide each of them by it.
If there are no common factors other than 1, then the ratio is already in its simplest form. In this case, the ratio 1000:311:29 has no common factors other than 1, so it is already in its simplest form.
It is worth noting that ratios in their simplest form cannot be further reduced. They represent the relative sizes or amounts of the quantities being compared. In this case, the ratio 1000:311:29 tells us that the first quantity is about 3.22 times larger than the second quantity, and the second quantity is about 10.72 times larger than the third quantity.
The factors of 1000 are: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000.
The factors of 311 are: 1, 311.
The factors of 29 are: 1, 29.
The only common factor of the three numbers is 1. Therefore, the ratio 1000:311:29 is already in its simplest form.
Hence, the simplified form of the ratio 1000:311:29 is 1000:311:29.
Visit here to learn more about ratio:
brainly.com/question/13419413
#SPJ11
Jim is trying to solve the system of equations. He begins by multiplying equation (1) by d and equation (2) by a. Before he can continue, his friend angela comes by and says, "no, you should have multiplied equation (1) by e and equation (2) by b. You're going to get the wrong answer. " is angela right? why or why not?.
Answers
It depends on the values of a,b,d and e in the equations , different values may lead to different answers.
What is linear equation ?
A linear equation is an equation in which the highest power of the variable is 1. Linear equations can be written in the form of y = mx + b, where m is the slope of the equation, x is the variable, and b is the y-intercept, the point where the line crosses the y-axis. These equations are called linear because they describe a straight line when graphed.
It depends on the specific equations and the values of a, b, d and e in the system of equations. Multiplying both sides of an equation by a non-zero constant does not change the solution set of the equation.
However, if Jim wants to use the method of elimination, which is multiplying one equation by a constant and adding or subtracting it from the other equation, then it is important to ensure that the coefficients of one variable in the two equations are opposite in sign after the multiplication. This will enable him to eliminate one variable and find the value of the other variable.
It depends on the values of a,b,d and e in the equations , different values may lead to different answers.
To learn more about linear equation visit : brainly.com/question/11897796
#SPJ4
Find the power set for the following sets (Write 3 examples of each)
a) Two sets A & B both having any 2 elements
b) Two sets A & B both having any 3 elements
c) Two sets A & B both having any 4 elements
Answers
Given statement solution is :- a) Power set for two sets A and B with any 2 elements:
Set A: {1, 2}, Set B: {3, 4}
Power set of A: {{}, {1}, {2}, {1, 2}}
Power set of B: {{}, {3}, {4}, {3, 4}}
b) Power set for two sets A and B with any 3 elements:
Set A: {1, 2, 3}, Set B: {4, 5, 6}
Power set of A: {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Power set of B: {{}, {4}, {5}, {6}, {4, 5}, {4, 6}, {5, 6}, {4, 5, 6}}
c) Power set for two sets A and B with any 4 elements:
Set A: {1, 2, 3, 4}, Set B: {5, 6, 7, 8}
Power set of A: {{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}
Power set of B: {{}, {5}, {6}, {7}, {8}, {5, 6}, {5, 7}, {5, 8}, {6, 7}, {6, 8}, {7, 8}, {5, 6, 7}, {5, 6, 8}, {5, 7, 8}, {6, 7, 8},
a) Power set for two sets A and B with any 2 elements:
Set A: {1, 2}, Set B: {3, 4}
Power set of A: {{}, {1}, {2}, {1, 2}}
Power set of B: {{}, {3}, {4}, {3, 4}}
Set A: {apple, banana}, Set B: {cat, dog}
Power set of A: {{}, {apple}, {banana}, {apple, banana}}
Power set of B: {{}, {cat}, {dog}, {cat, dog}}
Set A: {red, blue}, Set B: {circle, square}
Power set of A: {{}, {red}, {blue}, {red, blue}}
Power set of B: {{}, {circle}, {square}, {circle, square}}
b) Power set for two sets A and B with any 3 elements:
Set A: {1, 2, 3}, Set B: {4, 5, 6}
Power set of A: {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Power set of B: {{}, {4}, {5}, {6}, {4, 5}, {4, 6}, {5, 6}, {4, 5, 6}}
Set A: {apple, banana, orange}, Set B: {cat, dog, elephant}
Power set of A: {{}, {apple}, {banana}, {orange}, {apple, banana}, {apple, orange}, {banana, orange}, {apple, banana, orange}}
Power set of B: {{}, {cat}, {dog}, {elephant}, {cat, dog}, {cat, elephant}, {dog, elephant}, {cat, dog, elephant}}
Set A: {red, blue, green}, Set B: {circle, square, triangle}
Power set of A: {{}, {red}, {blue}, {green}, {red, blue}, {red, green}, {blue, green}, {red, blue, green}}
Power set of B: {{}, {circle}, {square}, {triangle}, {circle, square}, {circle, triangle}, {square, triangle}, {circle, square, triangle}}
c) Power set for two sets A and B with any 4 elements:
Set A: {1, 2, 3, 4}, Set B: {5, 6, 7, 8}
Power set of A: {{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}
Power set of B: {{}, {5}, {6}, {7}, {8}, {5, 6}, {5, 7}, {5, 8}, {6, 7}, {6, 8}, {7, 8}, {5, 6, 7}, {5, 6, 8}, {5, 7, 8}, {6, 7, 8},
For such more questions on Power Sets Examples for Sets
https://brainly.com/question/33026825
#SPJ8
a family consisting of one mother, one father, two daughters and a son is taking a road trip in a sedan. the sedan has two front seats and three back seats. if one of the pare
Answers
If one of the parents sits in the driver's seat, the other parent can sit in either the front passenger seat or one of the back seats. The remaining three children can then occupy the two remaining back seats.
The sedan has two front seats, so the parents can occupy one front seat and one back seat. This leaves two back seats available for the three children. Since the children cannot sit in the front seats due to safety regulations, they will occupy the remaining back seats.
In summary, one parent will sit in the driver's seat, and the other parent will choose between sitting in the front passenger seat or one of the back seats. The two daughters and the son will occupy the remaining back seats. This arrangement ensures that all family members can travel together comfortably and safely in the sedan during their road trip.
Please note that the calculation and conclusion are based on the assumption that the sedan has a total of five seats (two front seats and three back seats). If the sedan has a different seating arrangement, the solution may vary.
To know more about Passenger, visit
https://brainly.com/question/29466302
#SPJ11
Solve the system.
x - 5y + 4z=27
4x-3y-z-23
3x + 3y - 6z=-9
Answers
Answer:
Step-by-step explanation:
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method x-5y+4z=27,4x-3y-z=23,3x+3y-6z=-9 Tiger Algebra Solver.
What is the volume of a cube 1 1/2 inches wide 2 1/2 inches long and 4 inches high?
Answers
Answer:
231
Step-by-step explanation:
first of all it must be a cuboid bcoz a cube's edge is same i.e length =breadth= height.
now volume of cuboid =lbh
11/2×21/2×4
=231
ans....
Answer:
15 inches
Step-by-step explanation:
V = lwh
V = \(\frac{3}{2}\) · \(\frac{5}{2}\) · \(\frac{4}{1}\) = \(\frac{60}{4}\) = 15
A rectangular pigpen is to be built against a wall so that only three sides will require fencing. If p feet of fencing are to be used, the area of the largest possible pen is:
Answers
A rectangular pigpen is to be built against a wall so that only three sides will require fencing and if p feet of fencing are to be used, the area of the largest possible pen is (p/4)²
A rectangular pigpen is to be built against a wall so that only three sides will require fencing. If p feet of fencing are to be used. To Find: the area of the largest possible pen. Solution: Let ABC be a rectangular pen with A on the wall and the other vertices B and C on the ground.
Let AB = x, BC = y and AC = h (height of the pen)∴ p = x + y + h...[Given]⇒ h = p - (x + y) ...(i)Area (A) of the rectangular pen ABC = xy ...(ii)From equation (i) ⇒ h = p - (x + y) ...(i)By substituting this value in equation (ii) we get:⇒ A = x(p - x - y)⇒ A = px - x² - xy .....
(iii)To maximize A, we take the derivative of (iii) w.r.t x and equate it to zero.⇒ dA/dx = p - 2x - y = 0 ⇒ y = p - 2x .....(iv)Substituting equation (iv) in equation (i), we get⇒ h = 2x - p Substituting x = p/4 in equation (iii), we get the area of the largest possible pen.⇒ A = (p/4)²
Therefore, the area of the largest possible pen is (p/4)².Hence, option (C) is the correct answer.Note: This is a maximization problem of a function of two variables, given the relationship between those two variables. Therefore, the first step is to set up an equation that relates the variables.
Then find a function that you want to maximize or minimize and proceed accordingly.
To know more about maximize refer here:
https://brainly.com/question/30072001#
#SPJ11
Solve for x.
In(5x – 3) = 2
Need the answer ASAP please
Answers
Answer:
x = 1
Step-by-step explanation:
5x-3=2
Add 3 to both sides
5x=5
Divide both sides by 5
x = 1
Please help me I’ll make u brainliest I swear please

Answers
Since the provided equation is inconsistent, it cannot intersect.
What is equation?The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign. A mathematical statement known as an equation is made up of two expressions joined together by the equal sign. A formula would be 3x - 5 = 16, for instance. When this equation is solved, we discover that the value of the variable x is 7.
Here,
we can see that the second set of equation,
4x+2y=12
20x+10y=30
4/20=2/10≠12/30
1/5=1/5≠2/5
The given equation is inconsistent so it does not intersect.
To know more about equation,
https://brainly.com/question/2228446
#SPJ1
There were 80 runners to start a race. In the first half of the race, 2/5 of them dropped out. In the second half of the race, 5/8 of the remaining runners dropped out. How many runners finished the race?
Answers
The number of people who finished the race is 18.
How to calculate the value?In the first half of the race, 2/5 of them dropped out. The remaining will be:
= 1 - 2/5 = 3/5
In the second half of the race, 5/8 of the remaining runners dropped out. This will be:
= 5/8 × 3/5
= 3/8
Therefore, this that finished the race will be:
= 80 - [(2/5 + 3/8) × 80]
= 80 - (31/40 × 80)
= 80 - 62
= 18
The concept of fractions was used
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
Find FH
HELP
Please

Answers
Answer:
19
Step-by-step explanation:
FH is FG = GH which is 4+15=19
y? + y
y² - 2y ?
4y + 4
Find the simplified quotient.y? – 4y + 4
y(+ 1) (-2)(-2)
YO-2) 4(y + 1)
4(y + 1) y(+1)
(y-2)6-2) 0-2)
O
Y(+1) 419 + 1)
y0-2) (-2)(-2)

Answers
Answer:
that one is A and the second part is B :)
Shen drove 603 miles in 9 hours. At the same rate, how long would it take him to drive 335 miles?
Answers
Answer:
5 hours
Step-by-step explanation:
Since Shen drove at the same rate for both distances, we can use a proportion to solve for the time it would take him to drive 335 miles:
\(\frac{d_{1} }{t_{1} }=\frac{d_{2} }{t_{2} }\)
where d1 is 603 miles, t1 is 9 hours, d2 is 335, and t2 is the unknown value.
Thus, we can simply plug in everything to the equation and solve for t2:
\(\frac{603}{9}=\frac{335}{t_{2} }\\ 67=\frac{335}{t_{2} }\\ 67t_{2}=335\\ t_{2}=5\)
(*Note that 9 divides evenly into 603 and becomes 67, which is why I didn't cross-multiply first with he 603 and t2 and the 335 and 9, although you'd still get the same result for t2)
Thus, it would take Shen 5 hours to drive 335 miles.
You can check by finding the rate for both equations since we know that distance is equal to the product of rate and time (d = rt):
First equation: 603 miles = 9 hours * r mph
67 mph = r
603 = 67 * 9
Second equation: 335 miles = 5 hr * r mph
67 mph = r
335 = 67 * 5
in yoga class, all of the students are lined up according to height. Andy notices that the number of students who are taller than he is one-fourth the number of students who are shorter than he. Violetta notices that there are 3 times as many students who are taller than she than students who are shorter than she. How many students are the class is there are fewer than 40 students?
Answers
Answer: i think its 21! how idfk but it was on some website...dont hatecrime me!
Step-by-step explanation:
What are the two types of angles that are formed by interacting lines?
Answers
In geometry, angles are formed when two lines interact or intersect. There are two main types of angles that are formed by intersecting lines: acute angles and obtuse angles.
Acute angles are angles that measure less than 90 degrees. These angles are smaller in measure than a right angle. They are defined by the point where two lines meet, and the angle formed by the intersection of the lines is acute if the measure of the angle is less than 90 degrees.
Obtuse angles are angles that measure more than 90 degrees. These angles are greater in measure than a right angle. They are defined by the point where two lines meet, and the angle formed by the intersection of the lines is obtuse if the measure of the angle is greater than 90 degrees.
In summary, in geometry, angles are formed when two lines interact or intersect.
There are two main types of angles that are formed by intersecting lines: acute angles which are angles that measure less than 90 degrees, and obtuse angles which are angles that measure more than 90 degrees.
to know more about intersecting lines refer here
https://brainly.com/question/11297403#
#SPJ11
-8n+34=6(5+4n) help please
Answers
Answer:
n=1/8
Step-by-step explanation:
-8n+34=6(5+4n)
We move all terms to the left:
-8n+34-(6(5+4n))=0
We add all the numbers together, and all the variables
-8n-(6(4n+5))+34=0
We calculate terms in parentheses: -(6(4n+5)), so:
6(4n+5)
We multiply parentheses
24n+30
Back to the equation:
-(24n+30)
We get rid of parentheses
-8n-24n-30+34=0
We add all the numbers together, and all the variables
-32n+4=0
We move all terms containing n to the left, all other terms to the right
-32n=-4
n=-4/-32
n=1/8
Answer:
n= 0.125 or 1/8
Step-by-step explanation:
Distrubute 6 into (5+4n). It should give you 30+24n.
The equation should now look like this: -8n+34=30+24n.
Swap -8n with 30, giving -30+34=8n+24n. Add the numbers and the pronumerals together.
Now it will look like 4=32n. Divide the numbers, but unfortunately the number is small so the answer will have to be a decimal or a fraction. So it's 0.125 or 1/8.
If I didn't explain everything or something is wrong, please comment. I just signed up, so it's my first time using this.