what is a possible absolute value inequality to represent -1≤x≤5?
Answers
My possible absolute value is -3 ≤ lx - 2l ≤ 3
What is Absolute Value?
The absolute value (or modulus) l x l of a real number x is the non - negative value of x without regard to its sign. For example, the absolute value of 5 is 5 , and the absolute value of -5 is also 5. The absolute value of a number may be thought of as its distance from zero along real number line.
Now, the question is:
what is a possible absolute value inequality to represent -1≤x≤5
The representation of inequality -1≤x≤5 of absolute value will be :
-3 ≤ lx - 2l ≤ 3
Now, add 2 to each segment of the system of inequalities to solve for x while keeping the equation balanced:
-3 + 2 ≤ x -2 + 2 ≤ 3+2
-1 ≤ x ≤ 5
Hence, my possible absolute value is -3 ≤ lx - 2l ≤ 3
Learn more about Absolute Value at:
https://brainly.com/question/17037110
#SPJ1
Related Questions
Please help!!!
Have school tomorrow
This is due tomorrow!
I have no clue how to do this

Answers
Yes , ∠WGR is congruent ∠GHR because both angles are on one line.
What does the word "congruent" mean in math?
If it is possible to impose one geometric figure on the other such that their surface area coincides, that geometric figure is seen to be congruent, or to be in the connection of congruence.Congruent Figures Examples Two butterflies that are the same size and form. Two candy ice creams of equal size and shape. Two equal Lego bricks in respect of size and shape.a) No, ∠PHG is not congruent ∠MGH because both angles are not equal.
b) No, ∠RHG and ∠MGH are not supplementary angle because in supplementary angle is equal to 180° .
c) No, ∠SGW is not congruent ∠PHV.
d) Yes , ∠WGR is congruent ∠GHR because both angles are on one line.
Learn more about Congruent
brainly.com/question/12413243
#SPJ13
Find f^{-1}(x) for the function below. Do not put spaces between your characters. If no inverse exists then type "none".f(x)=x+5f^{-1}(x)=Answer

Answers
1) To find out the inverse function of a function we need to swap the variables, and then isolate the y variable on the left, like this:
\(\begin{gathered} f(x)=x+5 \\ y=x+5 \\ x=y+5 \\ x-y=y-y+5 \\ x-y=5 \\ -x+x-y=5-x \\ -y=5-x \\ y=x-5 \\ f^{-1}(x)=x-5 \end{gathered}\)Note that after that, we can isolate and then divide the whole function by -1
2) Hence, the answer is:
\(f^{-1}(x)=x-5\)Use the drop-down menus to complete the statement about the inequality d>3.
Answers
The inequality d > 3 has infinitely many solutions because 4 and any number to the right of 3 on the number line can be substituted for d to make this inequality true.
What are infinitely many solutions?In Mathematics, an equation or an inequality is said to have an infinitely many solutions when the left hand side and right hand side of the equation or inequality are the same and equal.
This ultimately implies that, an equation or an inequality would have infinitely many solutions when both sides of the equal sign are the same, and both the slope and y-intercept for the two lines are the same.
The given inequality d > 3 simply means that the variable d is greater than three (3). Therefore, d represents the set of all possible real numbers that are greater than 3 and from the right of 4 on the number line for d > 3 because it has infinitely many solutions.
Read more on infinitely many solutions here: https://brainly.com/question/14626049
#SPJ1
Complete Question:
Use the drop-down menus to complete the statement about the inequality d > 3.
The inequality d > 3 has _____ solutions because ______ can be substituted for d to make this inequality true.
Options: for the first one 0 1 2 8 9 Infinitely many
For the second one: No numbers only 1 number 4 and any number to the right of 3 on the number line
ABCDE is a convex pentagon. Given AB = 5, BC = 12, AE = 13, DE = 8, CD = 6, and m∠B=m∠D=90°. Find the area of ABCDE.
Answers
The diagonals AC and EC of the pentagon forms two right
triangles and on isosceles triangle, together which gives the
area of the pentagon.
Correct response:
The area of the convex pentagon is 104 square units.Which is the methods used to finding the area of a pentagonThe area of the convex polygon is found by the sum of the
areas of the three triangles that are formed by drawing two
diagonals facing the two 90° angles.
The given parameters are;
AB = 5
BC = 12
AE = 13
DE = 8
CD = 6
m∠B = m∠D = 90°
Required:
The area of the convex pentagon ABCDE
Solution:
The area of pentagon ABCDE = Right ΔABC + Right ΔCDE + ΔACE
Area of right triangle ΔABC = \(\frac{1}{2}\) × 5 × 12 = 30
Area of right triangle ΔCDE = \(\frac{1}{2}\) × 6 × 8 = 24
Length of AC = \(\mathbf{\sqrt{\overline{AB}^2 + \overline{BC}^2}}\)
Which gives; AC = \(\mathbf{\sqrt{5^2 + 12^2}}\) = 13
Length of EC = \(\mathbf{\sqrt{\overline{CD}^2+ \overline{DE}^2}}\)
Which gives; EC = \(\mathbf{\sqrt{6^2 + 8^2}}\) = 10
Therefore, ΔACE is an isosceles triangle
Base of ΔACE = EC
Therefore;
Height of isosceles triangle ΔACE = \(\mathbf{\sqrt{13^2 - 5^2}}\) = 12
Area of ΔACE = \(\mathbf{\frac{1}{2}}\) × 10 × 12 = 60
Therefore;
Area of the convex pentagon ABCDE = 30 + 24 + 60 = 104Learn more about finding the area of geometric figures here:
https://brainly.com/question/2279661
To vary two inputs or decision variables and see how the changes in these quantities change a single output, what kind of table can we use?
a. Pivot Table
b. One-way Table
c. Summary Table
d. Two-way Table
Answers
When we vary two inputs or decision variables and want to see how the changes in these quantities change a single output.
When we vary two inputs or decision variables and want to see how the changes in these quantities change a single output, the table we use is called the Two-way Table.A two-way table is a table that shows the frequency distribution of categorical data in two different ways. It has two rows and two columns with one categorical variable defining the row and the other defining the column.To display the distribution of one variable along one dimension and the distribution of the other variable along the other dimension, we use a two-way frequency table. It's the same as a contingency table, but it includes frequency counts for each mix of the two variables.A two-way table is used in statistics to show the distribution of data when two different variables are taken into account. It is created to make comparisons between data in a tabular format to highlight correlations or relationships between the variables. Hence, the correct answer is the option d. Two-way Table.
To know more about variable,
https://brainly.com/question/28248724
#SPJ11
PLEASE HELP ME ASAP!!!!!!!!

Answers
Answer:
-3(-1)=
Step-by-step explanation:
a washer and a dryer cost combined. the cost of the washer is two times the cost of the dryer. what is the cost of the dryer?
Answers
If a washer and dryer cost $750 and the cost of the washer is two times the cost of the dryer, then the cost of the dryer $250
The total cost of a washer and dryer combined = $750
The cost of the dryer = x
The cost of the washer is two times the cost of the dryer.
The cost of the washer = 2x
Then the equation will be
x + 2x = 750
Add the like terms of the equation
3x = 750
Move 3 to the right hand side of the equation
x = 750/3
x = $250
Hence, if a washer and dryer cost $750 and the cost of the washer is two times the cost of the dryer, then the cost of the dryer $250
The complete question is:
A washer and dryer cost $750 combined the cost of the washer is two times the cost of the dryer what is the cost of the dryer?
Learn more about equation here
brainly.com/question/14603559
#SPJ4
Translate Triangle A by vector (3, -1) to give triangle B.
Then, rotate your triangle B 180° around the origin to give triangle C.
Describe fully the SINGLE transformation that maps triangle A onto triangle C.

Answers
Answer:
Translation as Triangle A has been translated by vector (3,-1) to now being (-2,-3)
Translation as Triangle A has been translated by a vector (3,-1) to now being (-2,-3).
What is translation?The process of changing the location of the image on the coordinate system will be known as the translation.
A translation in mathematics does not turn a shape; instead, it moves it left, right, up, or down. They are congruent if the translated shapes (or the image) seem to be the same size as the original shapes. They have merely changed their direction or directions.
Given that Translate Triangle A by a vector (3, -1) to give triangle B. Then, rotate your triangle B 180° around the origin to give triangle C.
Triangle A translation ⇒ (3,-1)
The second translation = (-2,-3).
Therefore, the translation as Triangle A has been translated by a vector (3,-1) to now being (-2,-3).
To know more about translation follow
https://brainly.com/question/12861087
#SPJ2
Which function has an inverse that is also a function?
A. {(-4, 3), (-2, 7), (-1, 0), (4, -3), (11, -7)}
B. {(-4, 6), (-2, 2), 6-1, 6), (4, 2), (11, 2)}
C. {(-4,5), (-2, 9), (–1, 8), (4, 8), (11,4)}
D. {(-4, 4), (-2, -1), (–1, 0). (4.1), (11, 1)}

Answers
Given:
The different functions in the form of set of ordered pairs.
To find:
The function which has an inverse that is also a function.
Solution:
A relation is a function if there exists unique y-value for each x-value.
We know that the inverse transformation is defined as:
\((x,y)\to (y,x)\)
So, the inverse of function is also a function if their exists unique x-value for each y-value in the function.
In option A, all x-values and y-values are unique. It means, inverse of this function is also a function. So, option A is correct.
In option B, \(x=-4\) and \(x=-1\) when \(y=6\). It means, inverse of this function is not a function. So, option B is incorrect.
In option C, \(x=-1\) and \(x=4\) when \(y=8\). It means, inverse of this function is not a function. So, option C is incorrect.
In option D, \(x=4\) and \(x=11\) when \(y=1\). It means, inverse of this function is not a function. So, option D is incorrect.
Therefore, the correct option is A.
Can you please help me out with a question
Answers
We have to divide the shape into two
It will give us a Rectangle and a Trapezium
\(\begin{gathered} \text{Area of the shape }=\text{ area of Rectangle + area of Trapezium} \\ \text{Area of the shape = 50i}n^2\text{ }^{^{}}+34in^2 \\ Areaoftheshape=84in^2^{} \end{gathered}\)
Repeat the Question 2 for the following matrices A= ⎣
⎡
−3
−2
−8
4
3
8
0
0
1
⎦
⎤
,B= ⎣
⎡
1
0
0
0
−1
0
0
0
1
⎦
⎤
, b
= ⎣
⎡
1
0
3
⎦
⎤
. (I) (2 mark) Find the characteristic polynomial of matrix A. (II) (1 mark) Find eigenvalues of the matrix A. (III) (2 mark) Find a basis for the eigenspaces of matrix A. (IV) (1 mark) What is the algebraic and geometric multiplicities of its eigenvalues. (V) (2 mark) Show that the matrix is diagonalizable and find an invertible matrix P and a diagonal matrix D such that P −1
AP=D (VI) (2 marks) Find A 10
b
by writing b
as linear combination of eigenvectors of A. (VII) (2 marks) Find a formula for A k
for all non-negative integers k. (Can k be a negative integer?) (VIII) (1 mark) Use (VII) to find A 10
b
and compare it with what you found in (VI). (IX) (2 mark) Is A similar to B ? If yes, find an invertible matrix such that P −1
AP=B.
Answers
(I) The characteristic polynomial of matrix A is p(λ) = 2λ² - 2λ.
(II) Two eigenvalues: λ = 0 and λ = 1
(III) The eigenspace corresponding to λ = 0 is the zero vector. The eigenspace corresponding to λ = 1 is spanned by the vector [2, 0].
(IV) The algebraic multiplicity is 2 and the geometric multiplicity is 0. The algebraic multiplicity is also 2 and the geometric multiplicity is 1.
(V) The matrix A is not diagonalizable.
(VI) There is need to calculate A¹⁰ using a different approach. (VII) Aᵏ = Aᵏ ᵐᵒᵈ ⁵ for all non-negative integers k.
(VIII) A¹⁰ × b = [-2, 2]. (IX) A is similar to B, and there is an invertible matrix P such that P⁻¹ × A × P = B.
Here, we have,
(I) To find the characteristic polynomial of matrix A, we need to calculate the determinant of the matrix (A - λI), where λ is the eigenvalue and I is the identity matrix.
A - λI =
[1 - λ]
[1 - λ]
[-1 - λ]
[1 - λ]
det(A - λI) = (1 - λ)(1 - λ) - (1 - λ)(-1 - λ)
= (1 - λ)² - (-1 - λ)(1 - λ)
= (1 - λ)² - (λ + 1)(1 - λ)
= (1 - λ)² - (1 - λ²)
= (1 - λ)² - 1 + λ²
= (1 - 2λ + λ²) - 1 + λ²
= 2λ² - 2λ
Therefore, the characteristic polynomial of matrix A is p(λ) = 2λ² - 2λ.
(II) To find the eigenvalues of matrix A, we set the characteristic polynomial equal to zero and solve for λ:
2λ² - 2λ = 0
Factorizing the equation, we have:
2λ(λ - 1) = 0
Setting each factor equal to zero, we find two eigenvalues:
λ = 0 and λ = 1
(III) To find a basis for the eigenspaces of matrix A, we need to find the eigenvectors corresponding to each eigenvalue.
For λ = 0:
(A - 0I)v = 0, where v is the eigenvector.
Simplifying the equation, we have:
A × v = 0
Substituting the values of A and v, we get:
[1 0] [v1] = [0]
[1 -1] [v2] [0]
This gives us the system of equations:
v1 = 0
v1 - v2 = 0
Solving these equations, we find v1 = 0 and v2 = 0.
Therefore, the eigenspace corresponding to λ = 0 is the zero vector.
For λ = 1:
(A - I)v = 0
Substituting the values of A and v, we get:
[0 0] [v1] = [0]
[1 -2] [v2] [0]
This gives us the system of equations:
v2 = 0
v1 - 2v2 = 0
Solving these equations, we find v1 = 2 and v2 = 0.
Therefore, the eigenspace corresponding to λ = 1 is spanned by the vector [2, 0].
(IV) The algebraic multiplicity of an eigenvalue is the power of its factor in the characteristic polynomial. The geometric multiplicity is the dimension of its eigenspace.
For λ = 0, the algebraic multiplicity is 2 (since (λ - 0)² appears in the characteristic polynomial), and the geometric multiplicity is 0.
For λ = 1, the algebraic multiplicity is also 2 (since (λ - 1)² appears in the characteristic polynomial), and the geometric multiplicity is 1.
(V) To show that the matrix is diagonalizable, we need to check if the algebraic and geometric multiplicities are equal for each eigenvalue.
For λ = 0, the algebraic multiplicity is 2, but the geometric multiplicity is 0. Since they are not equal, the matrix is not diagonal
izable for λ = 0.
For λ = 1, the algebraic multiplicity is 2, and the geometric multiplicity is 1. Since they are not equal, the matrix is not diagonalizable for λ = 1.
Therefore, the matrix A is not diagonalizable.
(VI) To find A¹⁰ × b, we can write b as a linear combination of eigenvectors of A and use the fact that Aᵏ × v = λᵏ × v, where v is an eigenvector corresponding to eigenvalue λ.
We have two eigenvectors corresponding to the eigenvalue λ = 1: [2, 0]. Let's denote it as v1.
b = [-2, 2] = (-2/2) × [2, 0] = -1 × v1
Using the fact mentioned above, we can calculate A¹⁰ × b:
A¹⁰ × b = A¹⁰ × (-1 × v1)
= (-1)¹⁰ × A¹⁰ × v1
= 1 × A¹⁰ × v1
= A¹⁰ × v1
Since A is not diagonalizable, we need to calculate A¹⁰ using a different approach.
(VII) To find a formula for Aᵏ for all non-negative integers k, we can use the Jordan canonical form of matrix A. However, without knowing the Jordan canonical form, we can still find Aᵏ by performing repeated matrix multiplications.
A² = A × A =
[1 0] [1 0] = [1 0]
[1 -1] [1 -1] [1 -2]
A³ = A² × A =
[1 0] [1 0] = [1 0]
[1 -2] [1 -1] [-1 2]
A⁴ = A³ × A =
[1 0] [1 0] = [1 0]
[-1 2] [-1 2] [-2 2]
A⁵ =
A⁴ × A
= [1 0] [1 0]
= [1 0]
[-2 2] [-1 2] [0 0]
A⁶ = A⁵ × A =
[1 0] [1 0] = [1 0]
[0 0] [0 0] [0 0]
As we can see, starting from A⁵, the matrix Aⁿ becomes the zero matrix for n ≥ 5.
Therefore, Aᵏ = Aᵏ ᵐᵒᵈ ⁵ for all non-negative integers k.
(VIII) Using the formula from (VII), we can find A¹⁰ × b:
A¹⁰ * b = A¹⁰ ᵐᵒᵈ ⁵ × b
= A⁰ × b
= I × b
= b
We previously found that b = [-2, 2].
Therefore, A¹⁰ × b = [-2, 2].
(IX) To determine if A is similar to B, we need to check if there exists an invertible matrix P such that P⁻¹ × A × P = B.
Let's calculate P⁻¹ × A × P and check if it equals B:
P = [v1 v2] = [2 0]
[0 0]
P⁻¹ = [1/2 0]
[ 0 1]
P⁻¹ × A × P =
[1/2 0] [1 0] [2 0] = [0 0]
[ 0 1] [1 -1] [0 0] [0 0]
The result is the zero matrix, which is equal to B.
Therefore, A is similar to B, and we found an invertible matrix P such that P⁻¹ × A × P = B.
In this case, P = [2 0; 0 0].
learn more about polynomial of matrix:
brainly.com/question/16751698
#SPJ4
answer the question down below

Answers
The height down the wall, in centimeters that the ladder slipped would be 28. 61 cm.
How to find the height of the ladder ?To indicate the ladder's heights before and after slipping as h1 and h2, respectively, is imperative. The ladder maintains a constant length of 3 meters (300 cm) throughout the occurrence.
At first, the ladder's foot stands at a distance of 60 cm from the base of the wall. However, following its slip, the same foot travels an additional 80 cm further away, creating an increased gap between it and the base of the wall, totaling to 140 cm.
The determination of the initial and final heights can be achieved through relying on the Pythagorean theorem:
300 ² = h2² + 140 ²
h2 ² = 300 ² - 140 ²
h2 = 265. 33 cm
Slipped distance would be:
= h1 - h2
= 293. 94 cm - 265. 33 cm
= 28. 61 cm
Find out more on height at https://brainly.com/question/11002157
#SPJ1
Software companies work hard to produce software without bugs. A particular company claims that 85% of the software it produces is bug free. A random sample of size 200 showed 156 softwareprograms were bug free.
a. Calculate the mean of the sampling distribution of the sample proportion.
Answers
the sample proportion under probability has a mean sampling distribution of 82.
The population percentage is the major variable in the sampling distribution of this proportion, which has a quarter-um normal distribution. Variants include population proportion times one and population proportion divided by sample size. Additionally, we are aware that the population proportion is under the null hypothesis. 200 is the sample soil. When we enter the value of P into this calculation without normalisation, we can obtain the standing ovation as the variance's root. 025 in excess. The probability that we got a sample result of 188/58 or less is then calculated. We simply need to determine this left tail probability after that.
Learn more about probability here
https://brainly.com/question/12226830
#SPJ4
Lines m and n are parallel. The measure of angle 6 is 55 114 57.6 3 What is the measure of angle 1? 1552

Answers
Answer:
125 degree
Step-by-step explanation:
As m // n, so angle 2 and angle 6 is the same so angle 2 = 55 degree, then angle 1 + angle 2 = 180 degree, so angle 1 = 180 - 55 = 125 degree.
If it is helpful, please give me Brainliest.
Rewrite 6 2/3 as a mixed number.
Answers
Answer:
20/3
Step-by-step explanation:
Answer:
20/3
Step-by-step explanation:
3 5x + 6y = 32
12y - 4x = 8
Answers
Answer:
Step-by-step explanation: (x,y) (4,2)
(1 bookmark
the produce manager at the local pig & whistle grocery store must determine how many pounds of
bananas to order weekly. based upon past experience, the demand for bananas is expected to be 100,
150, 200, or 250 pounds with the following probabilities: 100lbs 0.20; 150lbs 0.25, 200lbs 0.35, 250lbs 0.20.
the bananas cost the store $.45 per pound and are sold for $.085 per pound. any unsold bananas at the
end of each week are sold to a local zoo for $.30 per pound. use your knowledge of decision analysis to
model and solve this problem in order to recommend how many pounds of bananas the manager should
order each week
Answers
As per the probability, the expected demand for bananas per week is 182.5 pounds.
To model this problem, we can use decision analysis, which involves identifying the possible outcomes, assigning probabilities to each outcome, and calculating the expected value of each decision.
In this case, the possible outcomes are the demand for bananas, which can be 100, 150, 200, or 250 pounds per week. The probabilities of each demand level are given as 0.20, 0.25, 0.35, and 0.20, respectively.
Let X denote the demand for bananas in pounds. Then, the expected demand for bananas, denoted as E(X), can be calculated as follows:
E(X) = 100(0.20) + 150(0.25) + 200(0.35) + 250(0.20) = 182.5
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Please prove the following:
Theorem 5. Let G be a group, and Z(G) it's center. If G|Z(G) is
cyclic, then G is abelian.
Answers
To prove the theorem, we need to show that if G has a cyclic center Z(G), then G is abelian (commutative), meaning that the group operation is commutative for all elements in G.Since this holds true for arbitrary elements a and b in G, we can conclude that G is abelian (commutative).
Proof:
Let G be a group with center Z(G), and assume that G|Z(G) is cyclic. This means that the factor group G/Z(G) is cyclic, which implies that there exists an element gZ(G) in G/Z(G) such that every element in G/Z(G) can be expressed as powers of gZ(G). In other words, for any element xZ(G) in G/Z(G), there exists an integer k such that (gZ(G))^k = g^kZ(G) = xZ(G).
Now, let's consider two arbitrary elements a and b in G. We want to show that ab = ba, which is the condition for G to be abelian.
Since a and b are elements of G, we can write them as a = z_1 × x and b = z_2 × y, where z_1 and z_2 are elements in Z(G), and x, y are elements in G.
Now, let's consider the product ab:
ab = (z_1 ×x)(z_2 × y)
Using the properties of group elements, we can rearrange the terms as follows:
ab = (z_1 × z_2) ×(x × y)
Since Z(G) is the center of G, we know that z_1 × z_2 = z_2 ×z_1, since both z_1 and z_2 commute with all elements in G.
Therefore, we have:
ab = (z_2 × z_1) × (x × y)
Now, we can rewrite this expression in terms of the factor group G/Z(G):
ab = (z_2 ×z_1) × (x × y) = (z_2 × z_1)(x ×y)Z(G)
Since (z_2 × z_1) is an element in Z(G), we can express it as a power of gZ(G) (since G/Z(G) is cyclic):
(z_2 × z_1) = (gZ(G))^m for some integer m
Substituting this back into the expression, we have:
ab = (gZ(G))^m (x × y)Z(G)
Using the fact that every element in G/Z(G) can be expressed as powers of gZ(G), we can write xZ(G) = (gZ(G))^p and yZ(G) = (gZ(G))^q for some integers p and q.
Substituting these into the expression, we have:
ab = (gZ(G))^m ((gZ(G))^p × (gZ(G))^q)Z(G)
Now, using the properties of exponents and powers in group operations, we can simplify this expression:
ab = (gZ(G))^m (gZ(G))^(p+q)Z(G)
Since G/Z(G) is a group, the product of two elements in the group is also an element in the group. Therefore, we can write this as:
ab = (gZ(G))^(m + p + q)Z(G)
Now, let's consider the expression (m + p + q). Since m, p, and q are integers, the sum (m + p + q) is also an integer. Let's denote it as k.
Therefore, we have:
ab = (gZ(G))^k Z(G)
Using the fact that every element in G/Z(G) can be expressed as powers of gZ(G), we can write this expression as:
ab = (g^k) Z(G)
Now, let's consider the element (g^k)Z(G) in G/Z(G). We know that (g^k)Z(G) is an element in G/Z(G), and every element in G/Z(G) can be expressed as powers of gZ(G).
Therefore, there exists an integer n such that (g^k)Z(G) = (gZ(G))^n.
Using the property of the factor group, we can rewrite this as:
(g^k)Z(G) = g^n Z(G)
Now, we can rewrite the expression ab as:
ab = (g^k) Z(G) = g^n Z(G)
Since ab and g^n are elements in G, and their images in the factor group G/Z(G) are equal, this implies that ab = g^n.
Therefore, we have shown that ab = g^n, which means that the product of any two elements in G is equal to the product of their corresponding powers of g.
Since this holds true for arbitrary elements a and b in G, we can conclude that G is abelian (commutative).
Hence, we have proved the theorem that if G has a cyclic center Z(G), then G is abelian.
Learn more about theorem here:
brainly.com/question/32715496
#SPJ11
I'll give you BRAINEST please help please plz
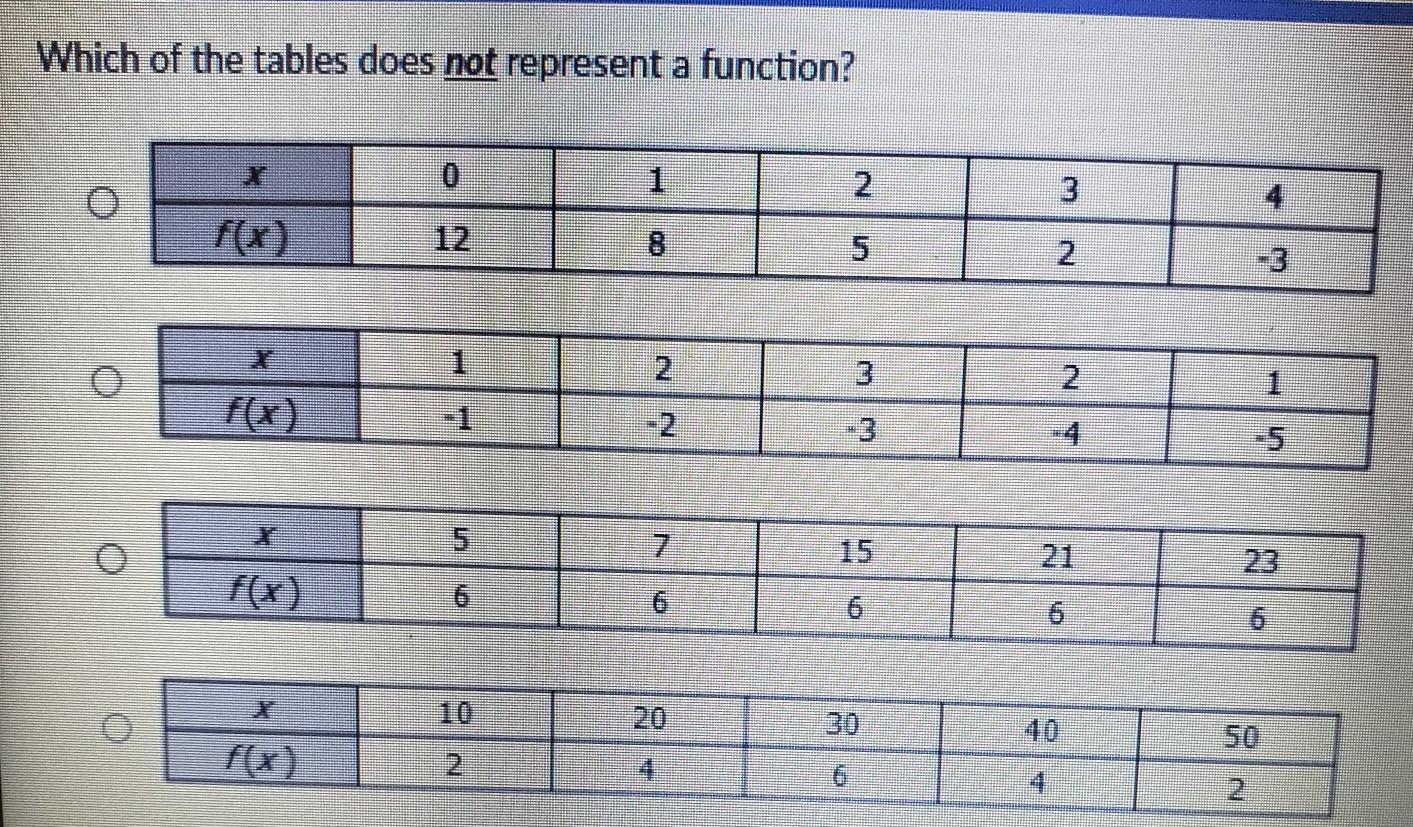
Answers
A function is a relation in which no two ordered pairs have the same first component and different second components.
We need to ask ourselves, does every first element (or input) correspond with EXACTLY ONE second element (or output)?
In this case, the answer is no. The input value of 1 goes with two output values, -1 and -5. The same goes with the input value of 2, which also goes with two output values: -2 and -4.
It only takes one input value to associate with more than one output value to be invalid as a function.
I also did the Vertical Line Test to show why Option 2 is not a function. The Vertical Line Test allows us to know whether or not a graph is actually a function. If a vertical line intersects the graph in all places at exactly one point, then the relation is a function.
However, the graph shows that the two vertical lines crossed the graphed twice (there are 2 points in each line). The graphed points failed the vertical line test. Therefore, Option 2 is NOT a function.
Please mark my answers as the Brainliest if you find my explanations helpful :)

-6x-7=4x-2. Can you show step by step explanation. thank u.
Answers
Answer:
x=-1/2
Step-by-step explanation:
-6x-7=4x-2
-6x-7+6x=4x+6x-2
-7=10x-2
-7+2=10x-2+2
-5=10x
-5/10=10x/10
x=-1/2
Hope this helps!
Solve each equation for x
2x+6x=1000
Answers
Answer:
x = 125
Step-by-step explanation:
2x + 6x is 8x
divide both sides by 8
x = 125
Answer:
x=125
Step-by-step explanation:
2x + 6x =1000
8x =1000
x=1000/8
x=125
Hope this helps
plz mark as brainliest
HELPP WORTH 30 points!!
Select all the correct answers.
If the measure of angle is 11, which statements are true?
sin (0) =
The measure of the reference angle is 60°.
The measure of the reference angle is 30°.
cos(8) √3
=
Otan(0) = 1
The measure of the reference angle is 45°.

Answers
Step-by-step explanation:
11pi/6 in radians.
pi = 180°
so,
pi/6 = 180/6 = 30°.
11pi/6 = 11×pi/6 = 11×30 = 330° or -30°.
the reference angle is the smallest (measured in absolute values) angle to the horizontal (x) axis.
so, that is then 30°.
so, which statements are true, and which are false ?
1.
sin(330°) = -1/2, because the angle is in the 4th quadrant and therefore below the x-axis, which makes the sine values negative.
sin(reference angle = 30°) would be +1/2, but that was not the statement.
so, this statement is false.
2.
the reference angle is 60°.
since we can see that it is actually 30°, this statement is false.
3.
the reference angle is 30°.
yes, that is true.
4.
cos(330°) = sqrt(3)/2.
yes, that is true.
this cosine is on the right side of the y-axis and therefore positive.
5.
tan(330°) = 1.
as tangent = sine/cosine, to be equal to 1 means that sine = cosine. which is not the case here.
this statement is false.
6.
the reference angle is 45°.
no, as 3. had shown, it is 30°.
so, this statement is false.
Idk what to do plz help fast 100pts

Answers
are we suppose to answer both
Answer:
C.)
Step-by-step explanation:
C.)
Point A and Point B lie on straight line H
Point A has coordinates (3,1) and point B has coordinates (p,21)
The gradient of line H is 5/4. Work out the value of p
Answers
Using the gradient formula, we can find the equation of the line H: y - 1 = 5/4(x - 3). Setting y = 21 and solving for x, we get the value of p is 19.
We can use the formula for calculating the gradient of a straight line:
Gradient = (y2 - y1) / (x2 - x1)
Where (x1, y1) and (x2, y2) are the coordinates of two points on the line.
We are given the gradient of the line as 5/4, and the coordinates of point A as (3,1). Let the coordinates of point B be (p,21). Then we can write the equation:
(21 - 1) / (p - 3) = 5/4
Simplifying this equation, we get:
20 / (p - 3) = 5/4
Multiplying both sides by (p - 3), we get:
20 = 5(p - 3) / 4
Multiplying both sides by 4, we get:
80 = 5(p - 3)
Dividing both sides by 5, we get:
16 = p - 3
Adding 3 to both sides, we get:
p = 19
Therefore, the value of p is 19.
To learn more about gradient please click on below link
https://brainly.com/question/25846183
#SPJ4
Please help! I can mark you brainliest!!

Answers
Answer:
x = 18.25
x = 60.
Step-by-step explanation:
Top question w/ the triangle. All triangles must equal 180 degrees (or else it's not a triangle or more than 1 triangle; which if you take Trig, you will encounter).
Knowing that all triangles are equal to 180, you can add all the angles given and set it equal to 180 to solve for x.
\(35+70+(4x+2)=180\\x = 18.25\)
If the question above asks for the value of x, the answer is 18.25.
Second question, these two angles MUST equal 180 degrees. Therefore, we can add the two angles and set it equal to 180 and solve for x.
\(x+2x=180\\3x=180\\x=60\)
If the question asks for the value of x, the answer is 60.
If the question asks for the missing side or the side with x, MAKE SURE YOU REPLACE X WITH IT'S NUMERICAL VALUE!!!
PLEASE PLEASE HELP ME!!! 25 POINTS!!!
Find YZ

Answers
Answer:
Is it not 2x + 12?
Step-by-step explanation:
Answer:
YZ =2x+12
= x + 6 ........( dividing the equation by 2 )
x=-6
yz = 2x + 12
= 2(-6) +12
= 0
if 2x+y=7 and y=2x-5 what is the value of x. solve using substitution or elimination
Answers
The value of x is found as 3 using the method of substitution.
What is the method of substitution?The substitution method is a straightforward method for algebraically solving a system of linear equations and determining variable solutions. It entails determining the value of x-variable in aspects of y-variable using the first equation and afterwards substituting or fixing the value of x-variable with in second equation, as the name implies.For the given expression, use substitution method to solve.
2x + y = 7 ........eq 1
y = 2x - 5 ........eq 2
Substitute the value of y from eq 2 in eq 1.
2x + 2x - 5 = 7
Solving;
4x = 7 + 5
4x = 12
x = 3
Thus, the value of x is found as 3.
To know more about the method of substitution, here
https://brainly.com/question/26609201
#SPJ10
if two variables are correlated, a change in one must directly produce a change in the other. t or f
Answers
If two variables are correlated, a change in one must directly produce a change in the other. (False)
What is the Correlation?Correlation is a statistical measure that indicates the extent to which two or more variables fluctuate together. It is a value between -1 and 1 that represents the strength of the relationship between two variables.
False. If two variables are correlated, a change in one may or may not directly produce a change in the other. Correlation means that there is a relationship between two variables, but it does not necessarily mean that one causes the other. It's possible for two variables to be correlated without any causal relationship between them.
To learn more about Correlation, Visit
brainly.com/question/28175782
#SPJ4
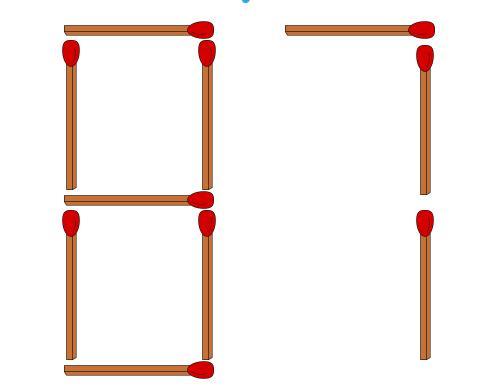
Move exactly two match sticks to make a prime number. How many different ways can you find to do this?
Answers
Answer: hello the image related to your question is missing attached below is the image
answer : 97 , 37, 67 done in three ( 3 ) different ways
Step-by-step explanation:
Prime number are number that can be divisible only by 1 and itself
Hence
The prime numbers that can be made by moving exactly two match sticks are : 97 , 37 , 67
and this can be done in in three (3) different ways
Write the correct partial fraction decomposition of: a) 2x²-3x/ x³+2x²-4x-8 b) 2x²-x+4 /(x-4)(x²+16)
Answers
the correct partial fraction decomposition of (a) 2x²-3x/ x³+2x²-4x-8 (b) 2x²-x+4 /(x-4)(x²+16) is 2/(x-2) - 1/(x²+4) & 0/(x-4) + (5x-1)/16(x²+16) respectively
a) Partial fraction decomposition of 2x²-3x/ x³+2x²-4x-8 the correct partial fraction decomposition of 2x²-3x/ x³+2x²-4x-8. The degree of the numerator is less than the degree of the denominator, so it is a proper fraction.In such a case, factorize the denominator and break the expression into partial fractions of the form :A/(x - p) + B/(x - q) + C/(ax² + bx + c)
Here, x³+2x²-4x-8 = x³ + 4x² - 2x² - 8x - 4x + 16 = (x²+4)(x-2)Also, 2x²-3x/ x³+2x²-4x-8= A/x + B/(x-2) + C/(x²+4)Let us find the values of A, B, and C.A(x-2)(x²+4) + B(x)(x²+4) + C(x)(x-2) = 2x² - 3x
On substituting x = 0,A(-2)(4) = 0A = 0On substituting x = 2,B(2)(8) = 2(2)² - 3(2)B = 2On substituting x = 1,C(1)(-1) = 2(1)² - 3(1)C = -1Therefore, 2x²-3x/ x³+2x²-4x-8= 2/(x-2) - 1/(x²+4)
b) Partial fraction decomposition of 2x²-x+4 /(x-4)(x²+16)We have to find the correct partial fraction decomposition of 2x²-x+4 /(x-4)(x²+16). This is a case of an improper fraction since the degree of the numerator is greater than or equal to the degree of the denominator.
It is important to factorize the denominator first. x²+16 = (x+4i)(x-4i)Here, 2x²-x+4 / (x-4)(x²+16) = A/(x-4) + (Bx + C)/(x²+16)Let us now find the values of A, B, and C.A(x²+16) + (Bx+C)(x-4) = 2x²-x+4On substituting x= 4A(32) = 2(4)² - 4 + 4A = 0On substituting x= 0C(-4) = 4C = -1/4On substituting x= 1B(1-4) - 1/4 = 2(1)² - 1 + 4B = 5/8Therefore, 2x²-x+4 /(x-4)(x²+16) = 0/(x-4) + (5x-1)/16(x²+16)
To know more about partial fraction visit :
https://brainly.com/question/30763571
#SPJ11