Using zero product property, find the values of x. (Hint: You must set factored parts equal to 0). (x+10)(2x-4)=0
I know there are two answers but I need an explanation please!! I want to understand this
Answers
Answer:
x = - 10, x = 2
Step-by-step explanation:
Given
(x + 10)(2x - 4) = 0
Equate each factor to zero and solve for x ( zero product property )
x + 10 = 0 ⇒ x = - 10
2x - 4 = 0 ⇒ 2x = 4 ⇒ x = 2
Related Questions
What is the Inverse Equation
f(x) =6x-1 ?? please I need help!
Answers
Answer:
\(f^{-1}(x)=\frac{x+1}{6}\)
Step-by-step explanation:
So we have the function:
\(f(x)=6x-1\)
To find the inverse function, switch x and f(x), change f(x) to f⁻¹(x), and solve for f⁻¹(x). Therefore:
\(f(x)=6x-1\)
Switch:
\(x=6f^{-1}(x)-1\)
Add 1 to both sides:
\(x+1=6f^{-1}(x)\)
Divide both sides by 6:
\(f^{-1}(x)=\frac{x+1}{6}\)
And that's our answer :)
Write the equation of the line in Point-Slope Form given the information below. Slope=-1/5 y-intercept=-3
Answers
Answer:
your correct answer is y=-1/5-3
Step-by-step explanation:
The linear equation of the line is y = -1/5x - 3 and y + 3 = -1/5(x - 0)
How to determine the line equation?The slope is given as:
m = -1/5
The y-intercept is given as:
c = -3
A linear equation in slope intercept form is represented as:
y = mx + c
So, we have:
y = -1/5x - 3
The equation in point slope form is calculated as follows:
y = -1/5x - 3
Add 3 to both sides
y + 3 = -1/5x
Express -1/5x as -1/5(x)
y + 3 = -1/5(x)
Subtract 0 from x
y + 3 = -1/5(x - 0)
Hence, the linear equation of the line is y = -1/5x - 3 and y + 3 = -1/5(x - 0)
Read more about linear equation at:
https://brainly.com/question/1884491
#SPJ9
can someone help please <3
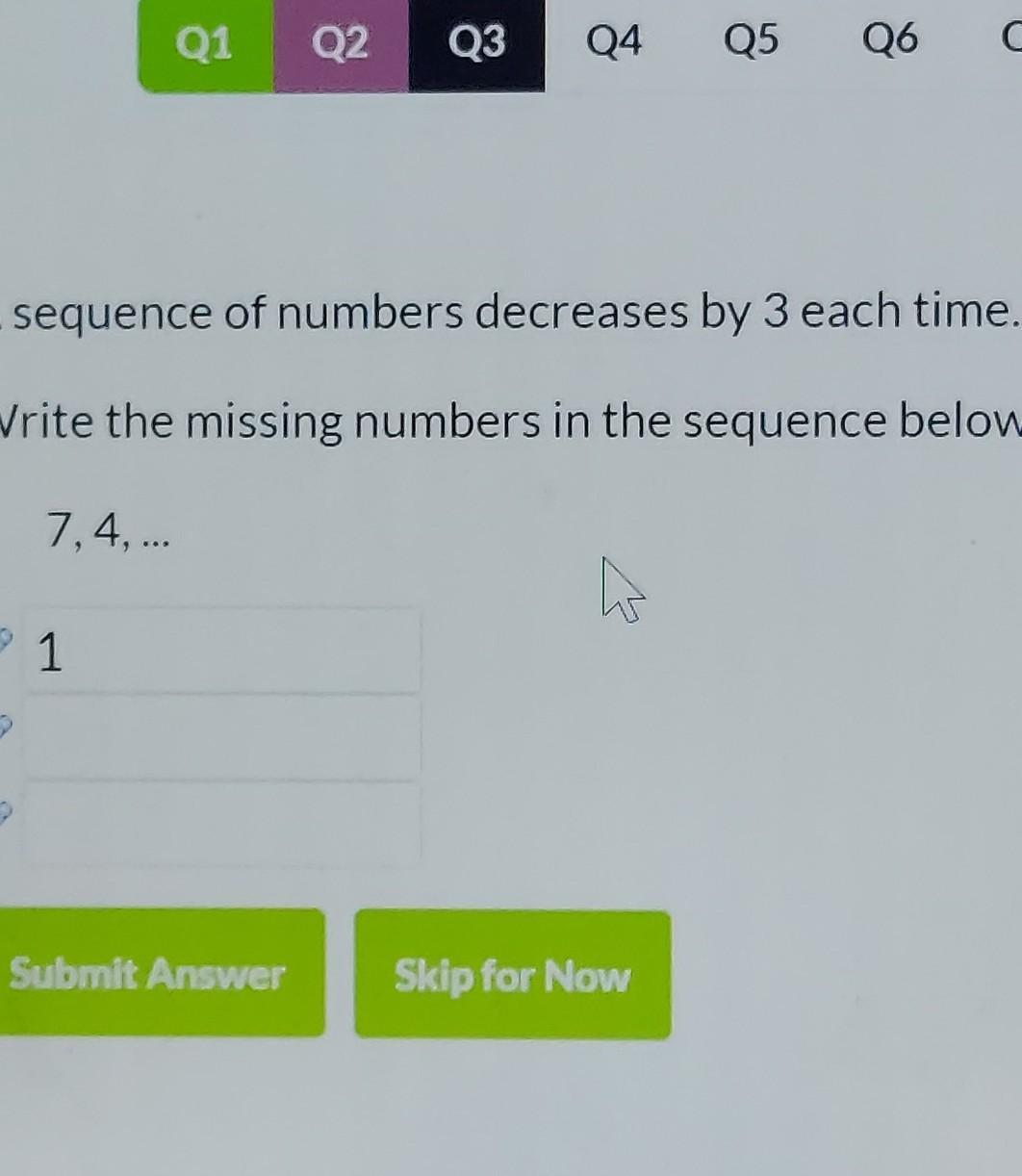
Answers
Answer:
-2
Step-by-step explanation:
one minus three equals to negative two
Assuming the chance of having a boy and a girl are equal. A family has five children. a) What is the probability of having exactly three boys? b) What is the probability of having at least three boys?
Answers
Assuming an equal chance of having a boy or a girl, (a) the probability of a family with five children having exactly three boys is 0.3125. (b) The probability of having at least three boys is 0.6875.
(a) To calculate the probability of having exactly three boys in a family with five children, we can use the binomial probability formula. The formula is \(P(X = k) = C(n, k) * p^k * q^{(n-k)}\) , where n is the total number of trials (number of children), k is the desired number of successes (number of boys), p is the probability of success (probability of having a boy), and q is the probability of failure (probability of having a girl).
In this case, n = 5, k = 3, p = 0.5, and q = 0.5. Plugging these values into the formula, we get P(X = 3) = C(5, 3) * 0.5³ * 0.5² = 10 * 0.125 * 0.25 = 0.3125.
(b) To calculate the probability of having at least three boys, we need to consider the probabilities of having exactly three boys, four boys, and five boys. We can calculate each of these probabilities using the same binomial probability formula.
The probability of having at least three boys is the sum of these three probabilities. In this case, P(X ≥ 3) = P(X = 3) + P(X = 4) + P(X = 5) = 0.3125 + C(5, 4) * 0.5⁴ * 0.5¹ + C(5, 5) * 0.5⁵ * 0.5⁰ = 0.3125 + 0.15625 + 0.03125 = 0.6875.
Therefore, the probability of having exactly three boys is 0.3125, and the probability of having at least three boys is 0.6875.
To learn more about binomial probability formula visit:
brainly.com/question/30764478
#SPJ11
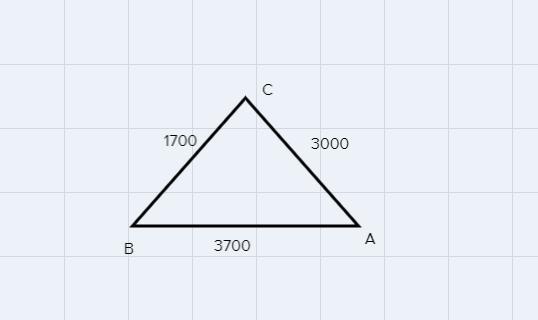
Use Law of Sines and Cosines to find the missing measurements. Round all answers to the nearest tenth. Please show work

Answers
Given:
The boat heads west for 3700 m. The other two sides lie the north for the first side, and their lengths are 1700m and 3000m.
The diagram for this model is
Using cosine law to find the angle of C.
\(c=\sqrt[]{a^2+b^2-2ab\cos C}\)Taking square on both sides, we get
\(c^2=a^2+b^2-2ab\cos C\)\(\cos C=\frac{a^2+b^2-c^2}{2ab}\)Substitute a=1700, b=3000 and c=3700, we get
\(\cos C=\frac{1700^2+3000^2-3700^2}{2\times1700\times3000}\)\(\cos C=\frac{-1800000}{10200000}=-0.17647\)\(\angle C=\cos ^{-1}(-0.17647)\)\(\angle C=100.164^o\)\(\angle C=100.2^o\)
Hence the measure of angle C is 100.2 degrees.
Using sine law,
\(\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\)Substitute a=1700, b=3000 and c=3700, and angle C=100.2 degrees, we get
\(\frac{\sin A}{1700}=\frac{\sin B}{3000}=\frac{\sin 100.2^o}{3700}\)\(U\text{se }\sin 100.2^o=0.9842.\)\(\frac{\sin A}{1700}=\frac{\sin B}{3000}=\frac{0.9842^{}}{3700}\)\(\frac{\sin A}{1700}=\frac{\sin B}{3000}=0.00027\)Consider
\(\frac{\sin A}{1700}=0.00027\)\(\sin A=0.00027\times1700\)\(\sin A=0.459\)\(\angle A=\sin ^{-1}(0.459)\)\(\angle A=27.322\)\(\angle A=27.3^o\)Hence the angle of A is 27.3 degrees.
Using triangle sum property, we get
\(\angle A+\angle B+\angle C=180^o\)\(\angle B=180^o-\angle A-\angle C\)\(\text{ Substitute }\angle A=27.3^o\text{ and }\angle C=100.2^o\text{, we get}\)\(\angle B=180^o-27.3^o-100.2^o\)\(\angle B=52.5^o\)
Hence the angle of B is 52.5 degrees.
Results:
\(\angle A=27.3^o\)
\(\angle B=52.5^o\)
\(\angle C=100.2^o\)
A coin is flipped five times. find the number of possible sets of heads and tails that have 2 heads.
Answers
The number of possible sets of heads and tails that have 2 heads is 11.
Given,
There is one coin and it is flipped five times.
First, we have to list out the outcome when we toss the coin five times.
(HHHHH), (HHHHT), (HHHTT), (HHTTT), (HTTTT), (TTTTT), (TTTTH), (TTTHH), (TTHHH), (THHHH), (THTHT), (HTHTH), (THHTT), (THHHT), (HTTTH), (HTTHH), (HTHHH), (THTTT), (TTHTH), (TTTHT), (TTHHT), (HHTHH), (TTHTT), (HHTTH), (HHTHT), (HTHTT), (THTHH), (THTTH), (HTHHT), (HHHTH)
Now, we can list out the possible sets with 2 heads.
(HHTTT), (TTTHH), (THTHT), (HTTHT), (HTTTH), (THHTT), (TTHHT), (TTHTH), (HTHTT), (THTTH), (HTHTT)
So, the number of possible sets of heads and tails that have 2 heads is 11.
Learn more about coin here: https://brainly.com/question/24158973
#SPJ4
Convert 102.221four to base ten
Answers
Answer:
4777
Step-by-step explanation:
Which is the longer amount? 4/10 of a dollar or 8/10 of a dollar?
Answers
Answer:
8/10 of a dollar is the correct answer
Step-by-step explanation:
explain how 6/12 and 4/8 are equal fractions
Answers
6/12 and 4/8 are equal fractions, as, when simplified, they share a simplified fraction.
Note that what you do to the denominator, you do to the numerator. Find common denominators for both fractions:
(4/8)/(2/2) = 2/4
(6/12)/(3/3) = 2/4
As you can tell, when they share a common denominator (4), the numerators are the same as well (3).
~
I need help with question 3 please
Answers
Answer:
there's nothing there..
Step-by-step explanation:
Answer:
i need the question to answer though
Step-by-step explanation:
PLEASE HELP!!
The diagram shows the cross-section ABCD of a sculpture in the shape of
a prism
with perpendicular height 9 cm.
AB = 14 cm, CD = 8cm, AD = 12cm and BC = 10cm
The height of the prism is also 9 cm.
What is the total surface area of the sculpture in cm2?
Type each step of your working on a separate line.

Answers
Answer:
99 (cm^2)
Step-by-step explanation:
Perpendicular to the AB segment at points D and C, the graph is divided into two triangles and a rectangle.
The area of the middle rectangle is equal to 8*9=72. The hypotenuse of the right triangle is 10cm, and one of the right sides is 9cm, so the other side is SQRT (10^2-9^2) = SQRT (19).
One side of the left triangle is 9cm long and the other side is 14-8-sqRT (19) = 6-sqRT (19) cm.
Then, add the area of the three parts.
72+9*sqrt(19)/2+9*(6-sqrt(19))/2=99 (cm^2)
Ames and Tonya are training for a race. Ahmed runs a mile in 8 minutes 30 seconds. Tonya runs a mile in 7 minutes 45 seconds. How much longer does it take Ahmed to run a mile than Tonya
Answers
The needed Ahmed takes 45 seconds longer than Tonya to run a afar.
Simplification involves applying rules of computation and algebra to remove gratuitous terms, factors, or operations from an expression.
Then,
To calculate how much longer it takes Ahmed to run a afar than Tonya, we need to find the difference between their handling times.
First, we need to convert the times to a common unit. Let's convert the times to seconds,
Ahmed's time 8 twinkles 30 seconds = ( 8 x 60) 30 = 510 seconds
Tonya's time 7 twinkles 45 seconds = ( 7 x 60) 45 = 465 seconds
Now we can find the difference in their times
Ahmed's time- Tonya's time = 510 seconds- 465 seconds = 45 seconds
thus, Ahmed takes 45 seconds longer than Tonya to run a afar.
Learn more about simplification here:
brainly.com/question/12501526
#SPJ4
Given the following information, choose the brand that is the better buy. Brand A: $1. 25 for 10 ounces Brand B: $1. 47 for 12 ounces Brand C: $1. 68 for 14 ounces Brand D: $1. 84 for 16 ounces a. Brand A b. Brand B c. Brand C d. Brand D
Answers
Option-D is correct that is Brand -D is better to buy because 16 ounces we have to pay $2.00 but it is $1.84 here saved $0.16.
Given that,
The brand that is the better buy.
Brand A: $1. 25 for 10 ounces
Brand B: $1. 47 for 12 ounces
Brand C: $1. 68 for 14 ounces
Brand D: $1. 84 for 16 ounces
We have to see which brand is better to buy.
Option D- Brand -D is better to buy because,
For brand-A
For $1.25 we get 10 ounces.
Brand- B as 12 ounces we have to pay $1.50 but it is $1.47 here saved $0.03
Brand- C as 14 ounces we have to pay $1.75 but it is $1.68 here saved $0.07
Brand- D as 16 ounces we have to pay $2.00 but it is $1.84 here saved $0.16
Therefore, Option-D is correct that is Brand -D is better to buy because 16 ounces we have to pay $2.00 but it is $1.84 here saved $0.16.
To learn more about ounces visit: https://brainly.com/question/29374025
#SPJ4
Can anyone help me with this

Answers
Answer:
yes
Step-by-step explanation:
Answer: Yes, am fairly certain it is a parallelogram.
Step-by-step explanation:
sorry about the crooked lines.


what is 5% of 5,000 interest rate
22 POINTS
Answers
5% of 5,000 interest rates equals to 250 interest rates.
F = G(m1m2/d2)
Solve for m1

Answers
Answer:
\(m_1=\frac{Fd^2}{Gm_2}\)
Step-by-step explanation:
\(F=G \left(\frac{m_1 m_2}{d^2} \right) \\ \\ \frac{F}{G}=\frac{m_1 m_2}{d^2} \\ \\ \frac{Fd^2}{G}=m_1 m_2 \\ \\ m_1=\frac{Fd^2}{Gm_2}\)
Consider a sample space with 7 elements. Let A be an event with 5 elements and B be an event with 4 elements. Let's assume that there are 2 repeated elements between both events.P(A y B) =A) 4/7B) 2/7C) 5/7D) 9
Answers
Option D (9) is not a probability and is not a possible answer choice for a probability question.
To find the probability of the intersection of events A and B (denoted as P(A ∩ B)), we need to know how many elements are in both A and B. Since there are 2 repeated elements between the events, this means that there are a total of 7 - 2 = 5 distinct elements between them.
Therefore, P(A ∩ B) = 5/7.
Note that none of the answer choices provided match this result exactly. Option A is the closest with a probability of 4/7, but this is the probability of A alone, not the intersection of A and B. Option B (2/7) is the probability of B alone and option C (5/7) is the probability of either A or B occurring, not the intersection.
Know more about probability here:
https://brainly.com/question/30034780
#SPJ11
is this table a function? why or why not?

Answers
Dianne measured the thickness of 1000 sheets of paper as 264mm. How thick is the sheet? Please hurry anyone!!!!!
Answers
Answer:
0.264 mm
Step-by-step explanation:
Number of sheets = 1000
Thickness of entire sheet = 264 mm
The thickness of the sheet is :
Thickness of entire sheet / number of sheets
264 mm / 1000
= 0.264 mm
what is 12(w-3) if w= 10
Answers
Hey there!
12(w - 3)
= 12(10 - 3)
= 12(10) + 12(-3)
= 120 - 36
= 84
OR
12(w - 3)
= 12(10 - 3)
= 12(7)
= 84
Therefore, your answer should be:
84
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
Point C is on line segment BD. Given BC=x+4,BC=x+4, CD=5x,CD=5x, and BD=5x+7,BD=5x+7, determine the numerical length of line CD.
Answers
The numerical length of line CD is 15
Solving linear equationsFrom the question, we are to determine the numerical length of line CD
From the given information,
Point C is on line segment BD
Thus, we can write that
BC + CD = BD
Also, from the given information
BC = x+4
CD = 5x
BD = 5x +7
Therefore,
x+4 + 5x = 5x + 7
6x + 4 = 5x + 7
Collect like terms
6x - 5x = 7 - 4
x = 3
Now, substitute the value of x into the equation for line CD
CD = 5x
CD = 5×3
CD = 15
Hence, the numerical length of line CD is 15
Learn more on Solving linear equations here: https://brainly.com/question/18883520
#SPJ1
For f(x) = x + 1 and g(x) = 2x^2 - x - 3, find (f/g)(x).
Answers
Answer:
\(\frac{1}{2x-3}\)
Step-by-step explanation:
(\(\frac{f}{g}\) )(x)
= \(\frac{f(x)}{g(x)}\)
= \(\frac{x+1}{2x^2-x-3}\) ( factorise the denominator )
= \(\frac{x+1}{(2x-3)(x+1)}\) ← cancel the common factor (x + 1) on numerator/ denominator
= \(\frac{1}{2x-3}\)
Is it the same as the mle if a random sample of 20 mechanics results in 15 correct diagnoses? explain.
Answers
The observed proportion of correct diagnoses in a random sample of mechanics is not necessarily the same as the MLE, as the MLE involves a more formal estimation procedure that considers the underlying probability distribution and maximizes the likelihood function based on the observed data.
The Maximum Likelihood Estimation (MLE) and the observed proportion of correct diagnoses in a random sample of mechanics are related concepts but not the same.
The MLE is a statistical method used to estimate the parameters of a probability distribution based on observed data. It seeks to find the parameter values that maximize the likelihood of observing the given data. In the case of a binomial distribution, which could be used to model the number of correct diagnoses, the parameter of interest is the probability of success (correct diagnosis) for each trial (mechanic).
In this context, if we have a random sample of 20 mechanics and observe that 15 of them made correct diagnoses, we can calculate the observed proportion of correct diagnoses as 15/20 = 0.75.
While the observed proportion can be considered an estimate of the underlying probability of success, it is not necessarily the same as the MLE. The MLE would involve maximizing the likelihood function, taking into account the specific assumptions and model chosen to represent the data. The MLE estimate may or may not coincide with the observed proportion, depending on the distributional assumptions and the specific form of the likelihood function.
In summary, the observed proportion of correct diagnoses in a random sample of mechanics is not necessarily the same as the MLE, as the MLE involves a more formal estimation procedure that considers the underlying probability distribution and maximizes the likelihood function based on the observed data.
Learn more about probability from
https://brainly.com/question/30390037
#SPJ11
Poisons are used to prevent rat damage in sugarcane fields. The U.S. Department of Agriculture is investigating whether rat poison should be located in the middle of the field or on the outer perimeter. One way to answer this question is to determine where the greater amount of damage occurs. If damage is measured by the proportion of cane stalks that have been damaged by the rats, how many stalks from each section of the field should be sampled in order to estimate the true difference between proportions of stalks damaged in the two sections, to within 0.02 with 90% confidence? (Assume equal number of stalks will be sampled from each section)
Answers
To estimate the difference between proportions, sample around 3355 stalks from each section of the field.
In order to estimate the true difference between proportions of stalks damaged in the two sections of the sugarcane field, we need to determine the sample size required to achieve a desired level of precision and confidence.
To estimate the required sample size, we can use the formula for sample size determination for estimating the difference between two proportions. This formula is based on the assumption of a normal distribution and requires the proportions from each section.
Let's denote the proportion of stalks damaged in the middle section as p1 and the proportion of stalks damaged in the outer perimeter as p2. We want to estimate the difference between these proportions to within 0.02 (±0.02) with 90% confidence.
To calculate the required sample size, we need to make an assumption about the value of p1 and p2. If we don't have any prior knowledge or estimate, we can use a conservative estimate of p1 = p2 = 0.5, which maximizes the required sample size.
Using this conservative estimate, we can apply the formula for sample size determination:
n = (Z * sqrt(p1 * (1 - p1) +\(p2 * (1 - p2)))^2 / d^2\)
where:
n is the required sample size per sectionZ is the z-score corresponding to the desired confidence level (90% confidence corresponds to a z-score of approximately 1.645)p1 and p2 are the estimated proportions of stalks damaged in the two sections (assumed to be 0.5)d is the desired precision or margin of error (0.02)Plugging in the values, we get:
n = (1.645 * sqrt(0.5 * (1 - 0.5) + 0.5 *\((1 - 0.5)))^2 / 0.02^2\)
n = (1.645 * sqrt\((0.25 + 0.25))^2\)/ 0.0004
n = (1.645 * sqrt\((0.5))^2\) / 0.0004
n =\((1.645 * 0.707)^2\) / 0.0004
n =\(1.158^2\) / 0.0004
n = 1.342 / 0.0004
n ≈ 3355
Therefore, the required sample size from each section of the field would be approximately 3355 stalks, in order to estimate the true difference between proportions of stalks damaged in the two sections to within 0.02 with 90% confidence.
Learn more about Sample Size
brainly.com/question/30100088
#SPJ11
To estimate the true difference between proportions of stalks damaged in the two sections of the sugarcane field, approximately 665 stalks from each section should be sampled.
In order to estimate the true difference between proportions of stalks damaged in the middle and outer perimeter sections of the sugarcane field, a representative sample needs to be taken from each section. The goal is to estimate this difference within a certain level of precision and confidence.
To determine the sample size needed, we consider the desired precision and confidence level. The requirement is to estimate the true difference between proportions of stalks damaged within 0.02 (i.e., within 2%) with 90% confidence.
To calculate the sample size, we use the formula for estimating the sample size needed for comparing proportions in two independent groups. Since an equal number of stalks will be sampled from each section, the total sample size required will be twice the sample size needed for a single section.
The formula to estimate the sample size is given by:
n = [(Z * sqrt(p * (1 - p)) / d)^2] * 2
Where:
n is the required sample size per section
Z is the Z-value corresponding to the desired confidence level (for 90% confidence, Z = 1.645)
p is the estimated proportion of stalks damaged in the section (unknown, but assumed to be around 0.5 for a conservative estimate)
d is the desired precision (0.02)
Plugging in the values, we can calculate the sample size needed for each section.
n = [(1.645 * sqrt(0.5 * (1 - 0.5)) / 0.02)^2] * 2
n ≈ 664.86
Rounding up, we arrive at approximately 665 stalks that should be sampled from each section.
Learn more about Sugarcan field
brainly.com/question/12925625
#SPJ11
Write -3.5 as a mixed number.
Answers
If it’s wrong I’ll correct it in the comments
How do I solve both equations ?

Answers
Answer:
a) 56.25 mph
b) $1.59/lb
Step-by-step explanation:
The units of the "unit rate" tell you the math operation you need to perform.
a)Miles per hour (mi/h) is found by dividing miles by hours.
(450 mi)/(8 h) = (450/8) mi/h = 56.25 mi/h
b)
Dollars per pound ($/pound) is found by dividing dollars by pounds.
($7.95)/(5 pounds) = (7.95/5) $/pound = 1.59 $/pound
__
Additional comment
In the context of unit rates, "per" means "divided by."
What makes a rate a "unit rate" is the "1 unit" in the denominator. For miles per hour, the denominator is 1 hour. For dollars per pound, the denominator is 1 pound.
Write the point-slope form of the equation for a line that passes through (6, –1) with a slope of 2.
The value of x1 is
.
The value of y1 is
.
The point-slope form of the equation is
Answers
Answer: See photo for details.
Step-by-step explanation:

Write a polynomial function of degree 6 with zeros 1, 2, and -i
Answers
On solving the provided question, we can say that, the required polynomial is - \((x^2 - x - 2)(x^2 + 1) = x^4 - x^3 - x^2 - x - 2\)
what is polynomial?In mathematics, a polynomial is an expression made up of variables (also known as indeterminates) and coefficients, using only addition, subtraction, multiplication, and non-negative integer powers of the variables. An equation that combines exponents, constants, and variables through addition, subtraction, multiplication, and division is referred to as a polynomial (not division by a variable). We are aware that a polynomial is a mathematical statement containing a variable (usually x). There are no variables in this situation if we regard the number "2" to be a polynomial. 2 is a polynomial of degree 0 thus.
given roots at \(-1 and 2\),
first two factors - (\(x + 1), (x - 2)\)
(x - i), then the conjugate must also be a factor. So n
\((x + 1)(x - 2)(x - i)(x + i)\)
\((x^2 - x - 2)(x^2 + 1) = x^4 - x^3 - x^2 - x - 2\)
To know more about polynomial visit -
https://brainly.com/question/11536910
#SPJ4
Which is the angle of depression from b to c
1.)<2
2.) <3
3.) <1
4.)<4

Answers
<2
Step-by-step explanation:
that the answer. because it below par
Draw the image of ABC under a dilation whose center is P and scale factor is 1/3

Answers
Answer:
there
Step-by-step explanation:

Answer:
khan
Step-by-step explanation:
