use your above answers to find an equation for the line through the point =(−2,3) perpendicular to the vector −3⃗ 6⃗ .
Answers
The equation of the line passing through the point (-2, 3) and perpendicular to the vector (-3, 6) is y = 1/2x + 4.
The given vector is (-3, 6), and to find the slope of a line perpendicular to this vector, we take the negative reciprocal of its slope. The slope of the given vector can be calculated as 6/(-3) = -2.
Since a line perpendicular to the given vector has a slope that is the negative reciprocal of -2, the slope of the perpendicular line is 1/2.
Using the point-slope form of a line, where (x1, y1) is a point on the line and m is the slope, we substitute (-2, 3) for (x1, y1) and 1/2 for m. This gives us the equation:
y - 3 = 1/2(x + 2).
Simplifying the equation, we obtain:
y - 3 = 1/2x + 1.
Finally, rearranging the equation to the standard form, we have:
y = 1/2x + 4.
Therefore, the equation of the line passing through the point (-2, 3) and perpendicular to the vector (-3, 6) is y = 1/2x + 4.
To learn more about slope click here, brainly.com/question/3605446
#SPJ11
Related Questions
What are the quadrants of the standard (x,y) coordinate plane below that contain points on the graph of the equation 4x - 2y = 8?

Answers
Answer: I III and IV
Step-by-step explanation:
The line intersects the x axis at (2,0) and the y axis at (0,-4) so the line goes through quadrants 1 3 and 4 so the answer is the middle or the 3rd from top
A boat travels 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the stream.
Answers
the speed of the boat is 5.418 km/h and the speed of the stream is 2.167 km/h
Let's define the variables:
B = speed of the boat in still water.
S = speed of the stream.
When the boat travels downstream, the total speed of the boat will be equal to the sum of the speed of the stream and the speed of the boat in still water:
speed = B + S
When the boat goes downstream, the speed will be:
speed = B - S
Now, also remember the relation:
speed*time = distance.
The given information is:
In 8 hours the boat can:
go 12 km upstream and 40km downstream.
We now need to define another variable, T, as the time that the boat travels upstream.
Then we can write this as:
12km = (B - S)*T
If the boat travels T hours upstream, and travels for a total of 8 hours, then the amount of time that travels downstream is 8h - T, then we can write:
40km = (S + B)*(8h - T)
Similarly, when we have:
"it can go 16 km upstream and 32 km downstream in the same time."
we can define a new variable T', and write:
16km = (B - S)*T'
32km = (S + B)*(8h - T')
Then we have a system of 4 equations:
16km = (B - S)*T'
32km = (S + B)*(8h - T')
40km = (S + B)*(8h - T)
12km = (B - S)*T
And we need to solve this for S and B.
To do it, we need to isolate one of the variables in one of the equations.
Let's isolate T in the last equation:
T = 12km/(B - S)
now we can replace that in the third equation to get:
40km = (S + B)*(8h - 12km/(B - S))
So now we have 3 equations:
16km = (B - S)*T'
32km = (S + B)*(8h - T')
40km = (S + B)*(8h - 12km/(S - B))
Now we need to do the same thing, this time let's isolate T' in the first equation and replace it in the second one:
T' = 16km/(B - S)
Replacing it in the second equation we get:
32km = (S + B)*(8h - T')
32km = (S + B)*(8h - 16km/(B - S))
So now we have two equations:
40km = (S + B)*(8h - 12km/(B - S))
32km = (S + B)*(8h - 16km/(B - S))
Let's simplify these:
40km = 8h*(S + B) - 12km*(S + B)/(B - S)
32km = 8h*(S + B) - 16km*(S+ B)/(B - S)
Now we can multiply both equations by (B - S) to get:
40km*(S - B) = 8h*(S + B)*(B - S) - 12km*(S + B)
32km*(S - B) = 8h*(S + B)*(B - S) - 16km*(S+ B)
Let's keep simplifying this:
40km*(B - S) + 12km*(S + B) = 8h*(S + B)*(B - S)
32km*(B - S) + 16km*(S+ B) = 8h*(S + B)*(B - S)
Now we get:
52km*B - 28km*S = 8h*(S^2 + B^2)
48km*B - 16km*S = 8h*(S^2 + B^2)
Notice that the right side of these equations is the same thing, then we can write:
52km*B - 28km*S = 48km*B - 16km*S
(52km - 48km)*B = (28km - 18km)*S
4km*B = 10km*S
B = (10/4)*S
B = (5/2)*S
Now we can replace this in one of our two equations, let's use the first one:
48km*B - 16km*S = 8h*(S^2 + B^2)
48km*(5/2)*S - 16km*S = 8h*( S^2 + ( (5/2)*S)^2)
Now we can solve this for S
104km*S = 8h*( S^2 + 25/4*S^2)
104km*S = 8h*(29/4*S^2) = 48h*S^2
104km*S = 48h*S^2
dividing at both sides by S we get:
104km = 48h*S
104km/48h = S = 2.167 km/h
And using B = (5/2)*S
We can find the speed of the boat:
B = (5/2)*2.167 km/h = 5.418 km/h
Then:
the speed of the boat is 5.418 km/h and the speed of the stream is 2.167 km/h
If you want to learn more about this topic, you can read:
https://brainly.com/question/17300107
Which set of ordered pairs (2%, y) could represent a linear function?
A = {(-4,5), (-1,-1), (0, -3), (1,-6)}
B = {(2, -5), (4, -3), (7, -1), (9, 1)}
–5, )
C= {(-2, –8), (-1,-6), (2, - 2), (4,2)}
D = {(-4,3), (-1,2), (2, 1), (5,0)}

Answers
Answer:
answer is D im pretty sure
Step-by-step explanation:
Hope the answer is right?!!!
Evaluate, in spherical coordinates, the triple integral of f(rho,θ,ϕ)=cosϕ, over the region 0≤θ≤2π, 0≤ϕ≤π/4, 3≤rho≤4
Answers
In the spherical coordinates, the triple integral of f(rho,θ,ϕ)=cosϕ, over the region 0≤θ≤2π, 0≤ϕ≤π/4, 3≤rho≤4 is \(79\pi /3\).
Spherical coordinates of the gadget denoted as (r, θ, Φ) is the coordinate machine specifically used in three-dimensional systems. In 3 dimensional area, the round coordinate gadget is used for finding the surface region. those coordinates specify 3 numbers: radial distance, polar angles, and azimuthal perspective.
To convert a factor from spherical coordinates to Cartesian coordinates, use equations x=ρsinφcosθ,y=ρsinφsinθ, and z=ρcosφ. To transform a factor from Cartesian coordinates to spherical coordinates, use equations ρ2=x2+y2+z2,tanθ=yx, and φ=arccos(z√x2+y2+z2).
Consider the function:
f(0,0,0)=cos
35057
Spherical Coordinates:
x=psin cos
y=psin sine
z = p cos
DV = p² sin dpdøde
1=[[[psin p cos dpdøde
003
= "deƒân (20)deſp°dp
-(2x) (1-1) (343-27)
12
pm (316
34
3
79/3
Learn more about spherical coordinates here https://brainly.com/question/4465072
#SPJ4
Find the surface area of the figure. Round to the nearest hundredth when necessary (2 decimal places). SA = hp + 2B

Answers
The calculated surface area of the figure is 3100.8 square feet
Calculating the surface area of the figurefrom the question, we have the following parameters that can be used in our computation:
SA = hp + 2B
From the figure, we have
B = 1/2 * (10 + 34) * 24.7 = 543.4
p = 2 * (34 + 19) = 106
h = 19
So, we have
SA = 19 * 106 + 2 * 543.4
Evaluate
SA = 3100.8
Hence, the surface area is 3100.8 square feet
Read more about surface area a
https://brainly.com/question/26403859
#SPJ1
The tables given are for the linear functions f(x) and g(x). What is the input value for which f(x)=g(x) is true?
x=____

Answers
-1, it's fairly clear just from the table...
Answer:
-1
Step-by-step explanation:
A line has a slope of 3/7. What is the slope of any line parallel to this line?
a) -7/3
b) 0
c) 3/7
d) 7/3
Answers
The slope of any line parallel to this line would be c) 3/7.
What are parallel lines?Parallel lines are those lines that are equal distances apart and often of the same length. So, for the given slope where we have parallel lines, we can expect to have lines of the same slope. Thus we can arrive at 3/7.
Note that parallel lines have the same slope. So, since the first slope is 3/7, we can expect the second to be the same thing.
Learn more about parallel lines here:
https://brainly.com/question/24607467
#SPJ2
There is 12 feet from the center of the room to the wall. How big is the floor? (JUST write the number: no units) *
Answers
Answer:
im gonna say 24
Step-by-step explanation:
Answer:
if the room is a square it would be 576 if it is 12 feet from the center of the room to the edge than if you make another line from the center to the opposite direction of the first line and push your new line to the edge of the room you would get 24 feet from one corner to another and if the room is a square then all sides will be the same length so all sides will be 24 feet. and the equation would be 24 times 24 and the answer to that equation would be 576HELPPP PLZZ
What is the radius of a cylinder that has a volume of 500 ft ³ and that is 10 ft tall?
Answers
Answer:
The answer is 3.98942, rounded its 3.99.
Step-by-step explanation:
Answer:
3.99 ft
Step-by-step explanation:
Volume of a cylinder = πr²h
π = 3.14
volume = 500 ft³
height = 10 ft
πr²h = 500
3.14×r²×10 = 500
r² = 500/3.14×10
= 15.92..
= √15.92
r = 3.9899.. ≈ 3.99 ft
Factor the expression.
24 + 7x − 5x2
Answers
Answer:
-(5x+8)(x - 3)
Step-by-step explanation:
add and subtract second term to expression and factor using grouping
What’s the name of the transformation???

Answers
Answer:
Translation
Step-by-step explanation:
Remember Translation as a 'Slide'
Answer:
translation
Step-by-step explanation:
hopes this help
Plsssss heeelppp assapppp

Answers
Answer:
(2,-16) (4,-32) (8,-64)
Step-by-step explanation:
Help, this situation is very urgent

Answers
The distance between point F and point G is 2√5, while the volume of the traffic cone is 628.32 in³. Lastly the scientific notation form of 34.6 x 10⁵ is 3.46 x 10⁶
Understanding Distance, Volume and Scientific NotationDistance Formula
The distance formula is derived from the Pythagorean theorem and is given by:
d = \(\sqrt{(x_{2} - x_{1})^2 + (y_{2} - y_{1})^2}\)
Given the coordinates of point F as (-1, 6) and point G as (3, 4), we can substitute these values into the distance formula:
d = \(\sqrt{(3 - (-1))^2 + (4 - 6)^2}\)
= \(\sqrt{(3 + 1)^2 + (-2)^2}\)
= √(16 + 4)
= √20
= 2√5
Therefore, the distance between point F and point G is 2√5 (approximately 4.47 units).
Volume
Use the formula for the volume of a cone, which is given by:
V = (1/3) * π * r² * h
Where:
V is the volume,
π is the constant approximately equal to 3.14,
r is the radius of the cone (half of the diameter), and
h is the height of the cone.
Given:
height = 2 feet (24 inches)
diameter = 10 inches
r = 10 inches / 2 = 5 inches
Now we can substitute the values into the volume formula:
V = (1/3) * 3.14 * (5 inches)² * 24 inches
= (1/3) * 3.14 * 25 square inches * 24 inches
= (1/3) * 3.14 * 600 cubic inches
≈ 628.32 cubic inches
Therefore, the approximate volume of the traffic cone is 628.32 cubic inches.
Scientific Notation
The number 34.6 × 10^5 can indeed be expressed in scientific notation. Scientific notation represents a number as a product of a decimal number between 1 and 10 (known as the coefficient) and a power of 10 (known as the exponent).
To express 34.6 × 10^5 in scientific notation, we can rewrite it as:
3.46 × 10^6
In this form, the coefficient is 3.46, and the exponent is 6.
Learn more about distance here:
https://brainly.com/question/28551043
#SPJ1
suppose that people's heights (in centimeters) are normally distributed, with a mean of 170 and a standard deviation of 5. we find the heights of 60 people. (you may need to use the standard normal distribution table. round your answers to the nearest whole number.) (a) how many would you expect to be between 165 and 175 cm tall? people (b) how many would you expect to be taller than 167 cm?
Answers
The expected number of people between 165 and 175 is 41.
The expected number of people taller than 168 is 39.
Given that the mean and standard deviation of people's heights (measured in centimeters) are 170 and 5 respectively. The heights of 60 people are revealed.
μ = 170
σ = 5
n = 60
(a) The probability would you expect to be between 165 and 175 cm tall;
P( 165 < x < 175 ) = P( (165 - 170)/5 < z < (175 - 170)/5 )
= P( -1 < z < 1 )
= P( z < 1) - P( z < -1 )
= 0.8413 - 0.1587
= 0.6826
Expected number of people between 165 and 175 = n * p
= 60 * 0.6826
= 40.956
≅ 41
(b) The probability would you expect to be taller than 167 cm;
P( x > 167 ) = P( z > (167 - 170)/5 )
= P( z > -0.6 )
= 0.7257
Expected number of people taller than 168 = n * p
= 60 * 0.7257
= 43.542
≅ 39
Hence,
The expected number of people between 165 and 175 is 41.
The expected number of people taller than 168 is 39.
To learn more about probability click here:
brainly.com/question/11234923
#SPJ4
help please ! brainliest to first correct answer
What is the solution for x2 –18x < –77?
x < –11 or x > 7
x < –7 or x > 11
–11 < x < 7
7 < x < 11
Question 2(Multiple Choice Worth 2 points)
(07.01 LC)
A two-variable inequality is shown in the graph.
upward opening parabola which is dashed with vertex at 1 comma 2, travels through points negative 1 comma 6 and 3 comma 6, with shading inside the curve
Which point is not included in the solution set for the inequality?
(–1, 3)
(0, 4)
(1, 5)
(2, 4)
Question 3(Multiple Choice Worth 2 points)
(07.01 MC)
Which graph represents the solution of y ≤ x2 + 2?
upward opening parabola formed with a dashed curve, vertex at 0 comma 2, and shading inside parabola
upward opening parabola formed with a dashed curve, vertex at 0 comma 2, and shading outside parabola
upward opening parabola formed with a solid curve, vertex at 0 comma 2, and shading inside parabola
upward opening parabola formed with a solid curve, vertex at 0 comma 2, and shading outside parabola
Question 4(Multiple Choice Worth 2 points)
(07.01 MC)
What is the range of the function f(x) = |x| + 5?
R: {f(x) ∈ ℝ | f(x) < 5}
R: {f(x) ∈ ℝ | f(x) ≥ 5}
R: {f(x) ∈ ℝ | f(x) > 5}
R: {f(x) ∈ ℝ | f(x) ≤ 5}
Question 5(Multiple Choice Worth 2 points)
(07.01 MC)
What is the solution to the inequality |2x + 3| < 7?
4 < x < 10
–5 < x < 2
x < 4 or x > 10
x < –5 or x > 2
Answers
The questions are illustrations of inequalities
The solution to the inequality is 7 < x < 11The range of the function is (c) R: {f(x) ∈ ℝ | f(x) > 5}The solution to the inequality is x < –5 or x > 2The solution to the inequalityThe inequality is given as:
x² - 18x < -77
Add 77 to both sides
x² - 18x + 77 < 0
Expand the inequality
x² - 7x - 11x + 77 < 0
Factorize the inequality
x(x - 7) - 11(x - 7) < 0
Factor out x - 7
(x- 7)(x - 11) < 0
Solve for x
x < 7 or x < 11
This means that the solution to the inequality is 7 < x < 11
The graph that represents the solutionThe inequality expression is given as:
y ≤ x² + 2
See attachment for the graph of the inequality
The range of the functionThe function is given as:
f(x) = |x| + 5
The smallest value of |x| is 0.
So, we have:
f(x) > 0 + 5
Evaluate
f(x) > 5
Hence, the range of the function is (c) R: {f(x) ∈ ℝ | f(x) > 5}
The solution to the inequalityThe inequality expression is given as:
|2x + 3| < 7
Remove the absolute expression
2x + 3 < 7 or 2x + 3 < -7
Subtract 3 from both sides
2x < 4 or 2x < -10
Divide both sides by 2
x < 2 or x < -5
Hence, the solution to the inequality is x < –5 or x > 2
Read more about inequality at:
https://brainly.com/question/11234618
#SPJ1

need help asap!!!!!! Marcel is performing the first test on his company’s new electric car. During the test, the electric car reaches a maximum speed of 81 mph.
The performance test results of the electric car can be modeled by the following table, where x represents time, in seconds at the start of the test, and y represents the speed, in miles per hour.
Answers
For this case we have the following variables:
x: represents time, in seconds at the start of the test.
y: represents the speed, in miles per hour.
We have then that:
x = 0 ---> y = 0
x = 12 ---> y = 0
Answer:
the electric car is not moving at 0 seconds and 12 seconds
I hope this helps!
the electric car is not moving at 0 seconds and 12 seconds
I hope this helps!
Al released his balloon from the 10-yard line, and it landed at the 16-yard line. If the ball reached a height of 27 yards, what equation represents the path of his toss?
Answers
The equation of the path of the parabola is y = a(x - 13)² + 27
Given data ,
To represent the path of Al's toss, we can assume that the path is a parabolic trajectory.
The equation of a parabola in vertex form is given by:
y = a(x - h)² + k
where (h, k) represents the vertex of the parabola
Now , the balloon was released from the 10-yard line and landed at the 16-yard line, we can determine the x-values for the vertex of the parabola.
The x-coordinate of the vertex is the average of the two x-values (10 and 16) where the balloon was released and landed:
h = (10 + 16) / 2 = 13
Since the height of the balloon reached 27 yards, we have the vertex point (13, 27)
Now, let's substitute the vertex coordinates (h, k) into the general equation:
y = a(x - 13)² + k
Substituting the vertex coordinates (13, 27)
y = a(x - 13)² + 27
To determine the value of 'a', we need another point on the parabolic path. Let's assume that the highest point reached by the balloon is the vertex (13, 27).
This means that the highest point (13, 27) lies on the parabola
Substituting the vertex coordinates (13, 27) into the equation
27 = a(13 - 13)² + 27
27 = a(0) + 27
27 = 27
Hence , the equation representing the path of Al's toss is y = a(x - 13)² + 27, where 'a' can be any real number
To learn more about parabola click :
https://brainly.com/question/24042022
#SPJ1
someone pls help im struggling if you do tysm ! <333 :)
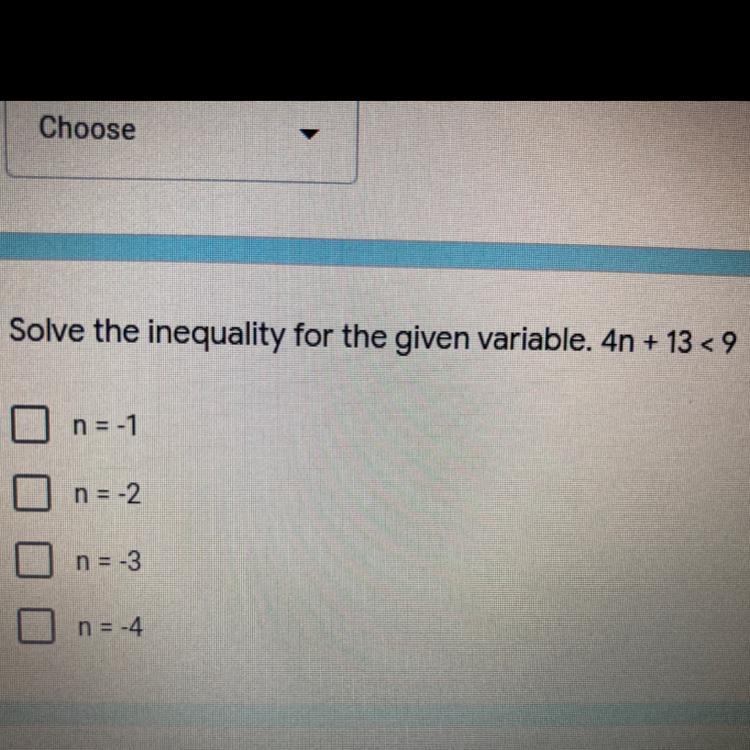
Answers
Answer:
everything except -1 will be the answer
Step-by-step explanation:
4n + 13 < 9
n < -1
if n is -1, the answer would be 9(INCORRECT)
if n is -2, the answer would be 5(CORRECT)
if n is -3, the answer would be 1(CORRECT)
if n is -4, the answer would be -3(CORRECT)
You graph the circle (x + 3)? + (y - 2)? = 25 and the line x = -8 in a coordinate plane. Which statement is
true?
A. The line is a tangent of the circle.
• B. The line is a secant of the circle.
• C. The line is a secant that contains the diameter of the circle.
• D. The line does not pass through the circle.
Answers
Answer:
D
Step-by-step explanation:
The circle has center (-3, 2) and radius 5. The line is a vertical line passing through the point (-8, 0).
We can see from the graph that the line does not intersect the circle at any point. Therefore, the correct answer is:
D. The line does not pass through the circle.
solve 6x - 3 = 3x + 12
Answers
Answer:
x=5
Step-by-step explanation:
May I have brainiest I'm trying to level up!
</3 PureBeauty
Answer:
x=5
Step-by-step explanation:
6x-3 = 3x +12
+3 +3
6x = 3x +15
-3x -3x
3x = 15
divided both sides by 3 to get your answer
Which value of x makes this equation true?-9x+15=3(2-x)
Answers
Step-by-step explanation:
-9x+15=3(2-x)
expand the bracket by the right hand side6-6x
2. collect like terms
-9x+15= 6-6x
15-6 = 6x+9x
11= 15x
3. divide both sides by the coefficient of X which is 15
x= 11/15
PLS HELP ME WITH THIS ASAPP

Answers
The value of the function f(x) at x = 1.477.
f(1.477) = 32.857
The value of the function g(x) at x = 20.
g(20) = 1.729
We have,
Two functions:
f(x) = b^x
g(x) = log_b(x)
Now,
From the table,
f(0.699) = b^0.699 = 5
Taking the logarithm of both sides with base b.
log_b(5) = 0.699
b = 5^(1/0.699)
b = 8.343
Now, we can find the value of f(1.477).
f(1.477) = b^1.477 = 8.343^1.477 = 32.857
Similarly, we can find the value of g(20).
g(20) = log_b(20) = log_8.343(20) = 1.729
Thus,
The value of the function f(x) at x = 1.477.
f(1.477) = 32.857
The value of the function g(x) at x = 20.
g(20) = 1.729
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
this is a two step equation

Answers
Answer:
b = -18
Step-by-step explanation:
to find be you need to isolate the variable. First, you have to multiply both sides by 13 to cancel the denominator. Then, add 8 to both sides to cancel the negative 8 on the left. You should be left with what x equals.
-8+b/13(13) = -2(13)
-8+b = -26
+8 +8
b = -18
Answer:
b = -18
Step-by-step explanation:
First multiply 13 on both sides which will give you
-8 + b = -26
Then add 8 to both sides and will give the answer
b = -18
3.5 as a fraction(simplest form) WITH STEPS
Answers
(3.5x10)/10
That can be further reduced to 7/2, since both numerator and denominator are dismissible by 5.
(3.5x10)/10
/5 /5
35/5=7
10/5=2
7/2 is the answer
Create an equation in the form y = asin(x - d) + c given the transformations below.
The function has a maximum value of 8 and a minimum value of 2. The function has also been vertically translated 1 unit up, and horizontally translated 10 degrees to the right.
Answers
The equation representing the given transformations is y = 3sin(x - 10°) + 3.
To create an equation in the form y = asin(x - d) + c given the transformations, we can start with the standard sine function and apply the given transformations step by step:
Vertical translation 1 unit up:
The standard sine function has a maximum value of 1 and a minimum value of -1.
To vertically translate it 1 unit up, we add 1 to the function.
This gives us a maximum value of 1 + 1 = 2 and a minimum value of -1 + 1 = 0.
Horizontal translation 10 degrees to the right:
The standard sine function completes one full period (i.e., goes from 0 to 2π) in 360 degrees.
To shift it 10 degrees to the right, we subtract 10 degrees from the angle inside the sine function.
This accounts for the horizontal translation.
Adjusting the amplitude:
To achieve a maximum value of 8, we need to adjust the amplitude of the function.
The amplitude represents the vertical stretch or compression of the graph.
In this case, the amplitude needs to be 8/2 = 4 since the original sine function has an amplitude of 1.
Putting it all together, the equation for the given transformations is:
y = 4sin(x - 10°) + 2
This equation represents a sine function that has been vertically translated 1 unit up, horizontally translated 10 degrees to the right, and has a maximum value of 8 and a minimum value of 2.
For similar question on standard sine function.
https://brainly.com/question/16300816
#SPJ8
from 9 am today until 9 am tomorrow, how many times will the hands of a standard 12-hour clock coincide?
Answers
The hands of a 12-hour clock will coincide 22 times from 9 am today until 9 am tomorrow.
In a 12-hour clock, the hands coincide when the minute hand and the hour hand are on the same hour marks. For example, when the minute hand and hour hand coincide at 12 o'clock, the next time they will coincide is at 1 o'clock.
The minute hand moves 12 times faster than the hour hand, so for every hour that passes, the minute hand travels 12 hour marks. In a 12-hour clock, the minute hand will travel 360 degrees and the hour hand will travel 30 degrees in one hour. The minute hand travels 12 times faster than the hour hand. We can calculate the number of coincidences between the minute hand and hour hand over 24 hours as follows:
For each hour, the hour hand moves 30 degrees and the minute hand moves 360 degrees.
Therefore, the difference in degrees between the minute hand and hour hand is 330 degrees.Therefore, the hands of a 12-hour clock will coincide 22 times from 9 am today until 9 am tomorrow.
Know more about Clock here:
https://brainly.com/question/12528769
#SPJ11
Find the area of the triangular pyramid below. Round your final answer to the nearest whole number

Answers
a restaurant offers a choice of 4 salads, 5 main courses, and 3 desserts. how many possible 3-course meals are there?
Answers
Using the Fundamental Counting Theorem, it is found that there are 60 possible 3-course meals.
Given,
In the question:
A restaurant offers a choice of 4 salads, 5 main courses, and 3 desserts.
To find the how many possible 3-course meals are there?
Now, According to the question:
Let's know:
What is the Fundamental Counting Theorem?
It is a theorem that states that if there are n things, each with ways to be done, each thing independent of the other, the number of ways they can be done is:
\(N=n_1\) × \(n_2\) × \(n_3\)... ×\(n_n\)
In this problem, considering the number of salads, main courses and desserts, we have that:
\(n_1=4 , n_2=5,n_3=3\)
The total number of options is given by:
N = 4 × 5 × 3
N = 60
Hence, Using the Fundamental Counting Theorem, it is found that there are 60 possible 3-course meals.
Learn more about Fundamental Counting Theorem at:
https://brainly.com/question/28384306
#SPJ4
A 90% confidence interval for the mean of a population is computed to be 135 to 160. Which one of the following claims would the interval tend to refute?A. The population mean is more than 110.B. The population mean is less than 150.C. The population mean is between 140 and 150.D. The population mean is more than 140.E. The population mean is less than than 125.
Answers
Therefore, the only claim that the interval would tend to refute is option E: The population mean is less than 125.
Based on the 90% confidence interval of 135 to 160, we can conclude that the population mean is likely to be within this interval with a 90% degree of confidence.
A. The claim that the population mean is more than 110 is not refuted by the confidence interval since the lower limit of the interval is above 110.
B. The claim that the population mean is less than 150 is not refuted by the confidence interval since the upper limit of the interval is above 150.
C. The claim that the population mean is between 140 and 150 is not refuted by the confidence interval since both values are within the interval.
D. The claim that the population mean is more than 140 is not refuted by the confidence interval since the lower limit of the interval is above 140.
E. The claim that the population mean is less than 125 is refuted by the confidence interval since the lower limit of the interval is above 125.
To know more about confidence interval,
https://brainly.com/question/27375978
#SPJ11
Please help its urgent

Answers
Answer:
4a=76°
2a=38°
X=104°
Step-by-step explanation:
the sum of angles triangle are 180°
so,
66°+4a+2a= 180°
or, 66°+6a=180°
or,6a= 180°-66°
or, a= 114°÷6
or, a= 19°
then, angle B = 4a= 4xa= 4x19°= 76°
angle C = 2x19°= 38°
lastly,
4a+x=180°[being straight angle]
76°+x=180°
x= 180°-76°
x= 104°.