Use the Pythagorean’s theorem to calculate the length of the hypotenuse of a right triangle with 17 as the length and 15 as the width
Answers
Answer:
\(\huge\boxed{\text{Around\ \ } 23}\)
Step-by-step explanation:
The Pythagorean Theorem states that
\(a^2 + b^2 = c^2\)
Where \(a\) is one leg of the triangle, \(b\) is the other, and \(c\) is the hypotenuse.
Since we know the legs and we need to find the hypotenuse \(c\), we can substitute inside the equation with the values 15 and 17.
\(15^2 + 17^2 = c^2\\\\225+289 = c^2\\\\514 = c^2\\\\c = \sqrt{514}\\\\c \approx 23\)
Hope this helped!
Answer:
Hypotenuse = 22.67
Step-by-step explanation:
\(a^2 + b^2 = c ^2\\\)
a = One Leg
b = Another Leg
c = Hypotenuse
\(17^{2} + 15^{2} = c^2\)
289 + 225 = \(c^2\)
514 = \(c^2\)
\(\sqrt{514} = c\)
c = 22.67
Related Questions
Find the matrix A of the linear transformationT(M)=[8097]M[8097]−1from U2×2 to U2×2 (upper triangular matrices) with respect to the standard basis for U2×2 given by{[1000],[0010],[0001]}.
Answers
The matrix A of the linear transformation T(M) with respect to the standard basis for U2×2 is given by:
T([1000]) = [8 0]
[0 0]
T([0010]) = [0 0]
[0 9]
T([0001]) = [0 1]
[0 0]
To find the matrix A of the linear transformation T(M), we need to apply T to each basis vector of U2×2 and express the result as a linear combination of the basis vectors for U2×2. We can then arrange the coefficients of each linear combination as the columns of the matrix A.
Let's begin by finding T([1000]). We have:
T([1000]) = [8097][1000][8097]^-1
= [8 0]
[0 0]
To express this result as a linear combination of the basis vectors for U2×2, we need to solve for the coefficients c1, c2, and c3 such that:
[8 0] = c1[1000] + c2[0010] + c3[0001]
Equating the entries on both sides, we get:
c1 = 8
c2 = 0
c3 = 0
Therefore, the first column of the matrix A is [8 0 0]^T.
Next, we find T([0010]). We have:
T([0010]) = [8097][0010][8097]^-1
= [0 0]
[0 9]
Expressing this as a linear combination of the basis vectors for U2×2, we get:
[0 0] = c1[1000] + c2[0010] + c3[0001]
Equating the entries on both sides, we get:
c1 = 0
c2 = 0
c3 = 0
Therefore, the second column of the matrix A is [0 0 0]^T.
Finally, we find T([0001]). We have:
T([0001]) = [8097][0001][8097]^-1
= [0 1]
[0 0]
Expressing this as a linear combination of the basis vectors for U2×2, we get:
[0 1] = c1[1000] + c2[0010] + c3[0001]
Equating the entries on both sides, we get:
c1 = 0
c2 = 1
c3 = 0
Therefore, the third column of the matrix A is [0 1 0]^T.
Putting all of this together, we have:
A = [8 0 0]
[0 0 1]
[0 0 0]
Therefore, the matrix A of the linear transformation T(M) is:
T([1000]) = [8 0]
[0 0]
T([0010]) = [0 0]
[0 9]
T([0001]) = [0 1]
[0 0]
To know more about linear transformation:
https://brainly.com/question/30514241
#SPJ4
Brainliest stars
21)
In which container is the probability of randomly selecting a red ball on one draw 3/7?

Answers
Answer: Your answer is going to be C)
Here is my explanation, very simple! So if you count all the balls together in answer's A) B) and D) there aren't 3 balls in each, so for example answer A) has 4 red ball's. B) only has 1 red ball, D) also has 1 ball, so C) is your only reasonable answer because although all the containers have a total of 7 ball's there is not enough for your probability. being said your container/answer is C!
Answer: c
Step-by-step explanation: the girl up there said it
Describe the data for a correlational research study and explain how these data are different from the data obtained in experimental and nonexperimental studies, which also evaluate relationships between two variables. A correlational study satisfies which conditions?
Answers
Answer:
Step-by-step explanation:
The workers' union at a particular university is quite strong. About 96 of all workers employed by the university belong to the workers' union. Recently, the workers went on strike, and now a local TV station plans to interview 4 workers (chosen at random) at the university to get their opinions on the strike. What is the probability that exactly 2 of the workers interviewed are union members?
Answers
The probability that exactly 2 of the workers interviewed are union members is approximately 0.044.
To solve this problem, we can use the binomial probability formula, which is:
\(P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)\)
where:
n is the sample size (number of workers being interviewed)
k is the number of successes we are interested in (in this case, 2 of the workers being union members)
p is the probability of success (in this case, the probability that a worker is a union member)
(n choose k) is the binomial coefficient, which represents the number of ways to choose k items from a set of n items (this can be calculated using the formula n! / (k! * (n - k)!))
Plugging in the values, we get:
\(P(X = 2) = (4 choose 2) * (0.96)^2 * (1 - 0.96)^(4 - 2)\)
\(= (6) * (0.96)^2 * (0.04)^2\)
= 0.04403136
Therefore, the probability that exactly 2 of the workers interviewed are union members is approximately 0.044.
To learn more about probability please click on below link.
https://brainly.com/question/30034780
#SPJ1
1050+815+250 using properties and mental math
Answers
Answer:
It 2115
Step-by-step explanation:
If you just did it a sum every thing you would get the answer. :)
Given: AABC, CD 1 AB, AC = BC Area of AABC = 32 cm?. • M
Answers
The value of CD is 9.92 cm
How to find this value?Given:
∆ABC,CD ⊥ AB,AC = BC,Area of ABC = 32 cm2,m∠A = 72°Find: CD
Triangle ABC is an isosceles triangle with base AB, because AC = BC. In isosceles triangle angles adjacent to the base are congruent. So,
m<A = <mB = 72°
The sum of the measures of all interior angles is 180°, thus
m<C = 180° -72° - 72° = 36°
The area of the triangle ABC is
AABC= 1/2AC.BC.sin<C
If we expand,
AC = 10.43cm
Consider right triangle ACD. In this triangle,
sin <A = CD/AC
sin 72° = CD/10.43
therefore,
CD = 9.92 cm.
Read more about geometry here:
https://brainly.com/question/24375372
#SPJ1
Given: ∆ABC, CD ⊥ AB, AC = BC, Area of ABC = 32 cm2, m∠A = 72°
Find: CD
Which of the following sets of ordered pairs represents a function? PLEASE HELP
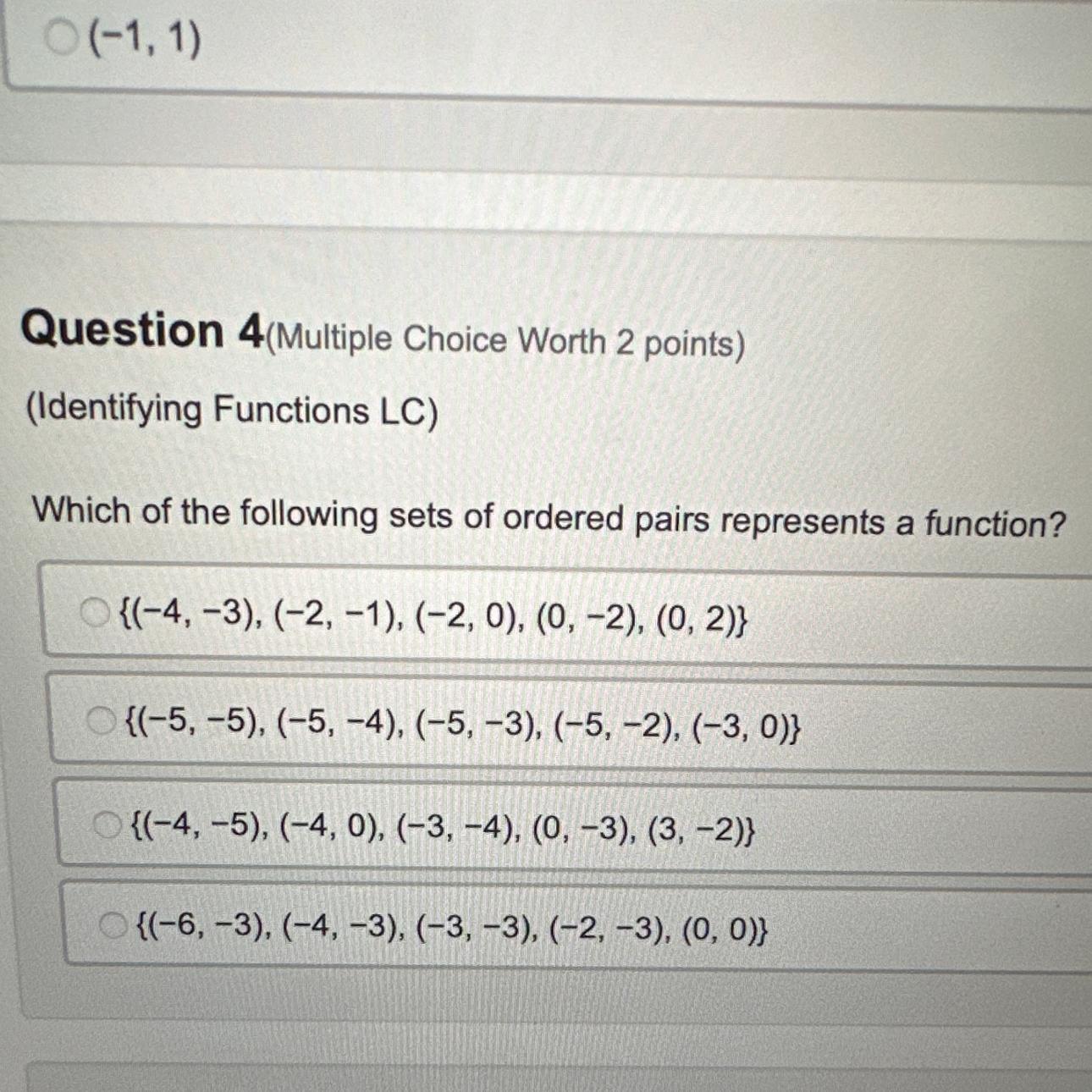
Answers
The set of ordered pairs that represents a function is (D) {(-6, -3), (-4, -3), (-3, -3), (-2, -3), (0, 0)}.
A set of ordered pairs represents a function if each unique input (x-value) is associated with only one output (y-value).
{(-4, -3), (-2, -1), (-2, 0), (0, -2), (0, 2)}
In this set, both (-2, -1) and (-2, 0) have the same x-value but different y-values. Therefore, this set does not represent a function.
{(-5, -5), (-5, -4), (-5, -3), (-5, -2), (-3,0)}
In this set, all the ordered pairs have the same x-value (-5). Since (-5, -5), (-5, -4), (-5, -3), and (-5, -2) have the same x-value but different y-values, this set does not represent a function.
{(-4, -5), (-4, 0), (-3, -4), (0, -3), (3, -2)}
In this set, (-4, -5) and (-4, 0) have the same x-value but different y-values. Therefore, this set does not represent a function.
{(-6, -3), (-4, -3), (-3, -3), (-2, -3), (0, 0)}
In this set, each unique x-value is associated with a single y-value. There are no repeated x-values. Therefore, this set represents a function.
To learn more on Sets click:
https://brainly.com/question/30705181
#SPJ1
8. Suppose Betty saves $200 each month in her 401(k) account. How much less will her monthly take-home pay be? (Assume a combined 20% state and federal income tax rate, as in the example.)
Answers
Note: Check the file attached below for the complete question
Answer:
Betty's monthly take home is $20 less
Step-by-step explanation:
Betty's monthly income = $2300
Betty's monthly savings = $200
Amount left after savings = $2300 - $200
Amount left after savings = $2100
Federal and State Income tax rate = 20% = 0.2
Tax amount paid = $420
Monthly take home = $2100 - $420
Monthly take home = $1680
Compared to $150 per month savings, Betty's monthly take home is $20 less

A line passes through the point ( 10,3 ) and has a slope of 1/2. write an equation in slope-intercept form for this line.
Answers
Answer:
\(\displaystyle y=\frac{1}{2}x-2\)
Solve
The point-slope form is represented with the formula:
\(y-y_1=m(x-x_1)\)
We are given a point \((x_1, y_1)\) and a slope: \(\displaystyle \frac{1}{2}\).
We are asked to solve this equation in slope-intercept form, which is:
\(y=mx+b\)
Givens
\(x_1: 10\\\\y_1: 3\\\\\displaystyle m: \frac{1}{2}\)
To solve:
1. Substitute the givens into the point-slope form equation:
\(y-y_1=m(x-x_1)\\\\\displaystyle y-3=\frac{1}{2}(x-10)\)
2. Simplify by using the distributive property, which states:
\(a(b+c)=ab+ac\)
\(\displaystyle y-3=\frac{1}{2}x-5\)
3. Simplify further by combining like terms:
\(\displaystyle y-3+3=\frac{1}{2}x-5+3\\\\\displaystyle y=\frac{1}{2}x-2\)
The final answer in slope-intercept form is:
\(\large \boxed{\displaystyle y=\frac{1}{2}x-2}\)
Answer:
y = 1/2x - 2
Step-by-step explanation:
Step 1:
y = mx + b Slope Intercept Form
Step 2:
y = 1/2x + b Equation
Step 3:
3 = 1/2 ( 10 ) + b Input x and y
Step 4:
3 = 5 + b Multiply
Step 5:
3 - 5 = b Subtract 5 on both sides
Step 6:
b = - 2
Answer:
y = 1/2x - 2
Hope This Helps :)
How do I solve this ?

Answers
Answer:
C. F(x) = 1/(x+7)(x-3)
Step-by-step explanation:
How do I solve this ?
A cycle wheel does 2169 full turns in 9 minutes. Work out the number of full turns per minute
Answers
Answer:
241 per min
Step-by-step explanation:
just take 2169/9 and get 241 per min
Answer:
241 turns in 1 minute.
Step-by-step explanation:
to find the answer 241 you need to divide 2169 by 9 which will get you 241 turns
So the wheel does 241 turns a minute.
HOPE IT HELPS YOU PLEASE MARK AS BRAINLIESTThe survey included a random sample of 640 western residents and 540 northeastern residents. 39% of the western residents and 51% of the northeastern residents reported that they were completely satisfied with their local telephone service. Find the 99% confidence interval for the difference in two proportions
Answers
Answer:
The 99% confidence interval for the difference in two proportions is (0.0456, 0.1944).
Step-by-step explanation:
Before building the confidence interval, we need to understand the central limit theorem and subtraction of normal variables.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
Subtraction between normal variables:
When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.
Western residents:
39% out of 640, so:
\(p_1 = 0.39\)
\(s_1 = \sqrt{\frac{0.39*0.61}{640}} = 0.0193\)
Eastern residents:
51% out of 540, so:
\(p_2 = 0.51\)
\(s_2 = \sqrt{\frac{0.51*0.49}{540}} = 0.0215\)
Distribution of the difference:
\(p = p_2 - p_1 = 0.51 - 0.39 = 0.12\)
\(s = \sqrt{s_2^2+s_1^2} = \sqrt{0.0215^2+0.0193^2} = 0.0289\)
Confidence interval:
\(p \pm zs\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
99% confidence level
So \(\alpha = 0.01\), z is the value of Z that has a p-value of \(1 - \frac{0.01}{2} = 0.995\), so \(Z = 2.575\).
The lower bound of the interval is:
\(p - zs = 0.12 - 2.575*0.0289 = 0.0456\)
The upper bound of the interval is:
\(p + zs = 0.12 + 2.575*0.0289 = 0.1944\)
The 99% confidence interval for the difference in two proportions is (0.0456, 0.1944).
Evaluate f (-3) for f(x) = x3 + 3x + 17
Answers
The output value of f( -3 ) in the function f(x) = x³ + 3x + 17 is -19.
What is the output value of f( -3 ) in the function?Given the function in the question:
f(x) = x³ + 3x + 17
To evaluate f(-3) for the function f(x) = x³ + 3x + 17, we simply substitute -3 for x in the expression and calculate the result.
f(x) = x³ + 3x + 17
Plug in x = -3
f(-3) = (-3)³ + 3(-3) + 17
First, let's calculate (-3)³, which means raising -3 to the power of 3:
(-3)³ = -3 × -3 × -3 = -27
Next, let's calculate 3(-3):
3(-3) = -9
Now, we can substitute these values into the expression:
f(-3) = -27 + (-9) + 17
Simplifying further:
f(-3) = -27 - 9 + 17
f(-3) = -36 + 17
f(-3) = -19
Therefore, the output value of f(-3) is -19.
Learn more about functions here: brainly.com/question/2541698
#SPJ1
All four of these inequalities are true. Use them to find the single whole-number value of g. Use that whole number to unlock the door. Your answer g>0 g≤100 4 5.5 is greater than g?
Answers
To find the value of g, we need to use the inequalities given. Since g>0 and g≤100, we know that g must be a whole number between 1 and 100.
The other two inequalities are not useful for finding g, so we can ignore them.
We don't know what value of g is, but we do know that 5.5 is greater than g. This means that g must be less than 5.5.
The only whole number between 1 and 100 that is less than 5.5 is 5.
So the value of g is 5, and that is the whole number you can use to unlock the door.
I don't understand anything about angles may u help me please

Answers
Answer:
125 degrees
Step-by-step explanation:
Just add the two angles given
What is the domain and range for
ƒ(x)= -√25-x^2
Answers
First rearrange and solve for sqrt of 25(which is 5)
ƒ(x)= -x^2-5
range: y\(\le\)5
domain: x x=can be anything because all values are defined
I need help with this please

Answers
Answer:
76.13.76 m^2
Step-by-step explanation:
Rectangle = 92 x 56
Rectangle = 5152
Circle = (3.14) x (56/2)^2
Circle = (3.14) x (28)^2
Circle = 2461.76
Total = 5152 + 2461.76
Total = 76.13.76 m^2
A box is 45cm long and 32cm wide when 36000cm^3 of sand is put into it what is the height of the sand
Answers
The height of the sand is 25cm
How to calculate height?
First the volume formula is height × long × wide. So, we can calculate height by dividing the volume by the long and wide.
= 36,000 ÷ 45 ÷ 32
= 25cm
Thus, the height of the sand is 25cm
Learn more about volume here:
brainly.com/question/1578538
#SPJ1
HELP!!!Joe can type 40 words every 2 minutes. How many words can he type in 5 minutes?
Answers
Answer:100
Step-by-step explanation:
40+40 =80 +20=100
mega mart sells a large 5kg cake for $2500 while a 2kg chocolate cake cost $1200 what is the cheapest price sam would payfor 10kg of cake for the party
Answers
The cheapest price Sam would pay for 10kg of cake for the party is $5000 from Mega Mart.
To find the cheapest price Sam would pay for 10kg of cake for the party, we need to compare the prices of the available cakes and determine the most cost-effective option.
At Mega Mart, a 5kg cake costs $2500.
Therefore, the price per kilogram for this cake is:
Price per kilogram at Mega Mart = $2500 / 5kg = $500/kg.
At the same time, a 2kg chocolate cake costs $1200.
So, the price per kilogram for this cake is:
Price per kilogram for the chocolate cake = $1200 / 2kg = $600/kg.
Now, let's calculate the total price for 10kg of cake from each option:
Total price at Mega Mart for 10kg = $500/kg \(\times\) 10kg = $5000.
Total price for 10kg of chocolate cake = $600/kg \(\times\) 10kg = $6000.
Comparing the two options, we see that the Mega Mart cake is the more cost-effective choice.
Sam would pay a total of $5000 for 10kg of cake from Mega Mart, whereas the chocolate cake would cost $6000 for the same quantity.
Therefore, the cheapest price Sam would pay for 10kg of cake for the party is $5000 from Mega Mart.
In summary, Sam would pay the cheapest price of $5000 to purchase 10kg of cake for the party from Mega Mart.
For similar question on cheapest price.
https://brainly.com/question/1153322
#SPJ8
The countries of Europe report that 46% of the labor force is female. The United Nations wonders if the percentage of females in the labor force is the same in the United States. Representatives from the United States Department of Labor
plan to check a random sample of over 10,000 employment records on file to estimate a percentage of females in the United States labor force.
5) The representatives from the Department of Labor want to estimate a percentage of females in the United States
labor force to within +/- 5%, with 90% confidence. How many employment records should they sample?
6) They actually select a random sample of 525 employment records, and find that 229 of the people are females. Create the confidence interval.
7) Interpret the confidence interval in this context.
8) Explain what 90% confidence means in this context.
9) Should the representatives from the Department of Labor conclude that the percentage of females in their labor force is lower than Europe's rate of 46%? Explain.
Answers
5. At least 676 employment records, 6. the proportion of females in the sample is 0.4362, 7. confidence interval is (0.401, 0.471), 8. 90% of those intervals would contain the true population proportion, 9. cannot conclude .
Describe Population Proportion?In statistics, population proportion refers to the proportion or percentage of individuals in a population that have a particular characteristic or attribute of interest.
5. To estimate a percentage of females in the United States labor force to within +/- 5%, with 90% confidence, we need to use the formula:
n = (z² × p × q) / E²
where:
n is the sample size we need to estimate the population proportion
z is the z-score associated with the desired level of confidence (in this case, 90%, so z = 1.645)
p is the estimated proportion of females in the population (we don't know this yet, so we use 0.5 as a conservative estimate)
q is the complement of p (q = 1 - p)
E is the maximum error we are willing to tolerate (in this case, 5%, so E = 0.05)
Plugging in the values, we get:
n = (1.645² × 0.5 × 0.5) / 0.05² = 676
So, the representatives from the Department of Labor should sample at least 676 employment records.
6. The sample size they actually selected is 525, and the proportion of females in the sample is 229/525 = 0.4362.
7. The confidence interval for the population proportion of females in the labor force is:
0.4362 ± 1.645 × √[(0.4362 × 0.5638) / 525] = (0.401, 0.471)
This means that we are 90% confident that the true proportion of females in the United States labor force is between 40.1% and 47.1%.
8. 90% confidence means that if we repeated the sampling process many times and calculated a confidence interval for each sample, about 90% of those intervals would contain the true population proportion.
9. We cannot conclude that the percentage of females in the US labor force is lower than Europe's rate of 46% based on this sample. The confidence interval includes the value of 46%, so it is possible that the true proportion is not significantly different from Europe's rate. However, we cannot say for certain without conducting hypothesis testing.
To know more about interval visit:
https://brainly.com/question/15290865
#SPJ1
Two cars leave the same point at the same time travelling in opposite directions. one car travels west at 20 mph and the other travels east at 60 mph. In how many hours will they be 280 miles apart?
Answers
It will take 3.5 hours for the two cars to be 280 miles apart.
To determine the time it takes for the two cars to be 280 miles apart, we can use the concept of relative velocity.
Since the cars are traveling in opposite directions, their velocities can be added together to find their relative velocity:
Relative velocity = Velocity of car traveling east + Velocity of car traveling west
Relative velocity = 60 mph + 20 mph
Relative velocity = 80 mph
The relative velocity of the cars is 80 mph, which means that they are moving away from each other at a combined speed of 80 mph.
To find the time it takes for them to be 280 miles apart, we can use the formula:
Time = Distance / Speed
Plugging in the values, we have:
Time = 280 miles / 80 mph
Time = 3.5 hours
Therefore, it will take 3.5 hours for the two cars to be 280 miles apart.
During this time, the car traveling east would have covered a distance of 60 mph × 3.5 hours = 210 miles, while the car traveling west would have covered a distance of 20 mph × 3.5 hours = 70 miles.
The sum of these distances is indeed 280 miles, confirming the result.
For more questions on relative velocity.
https://brainly.com/question/11418015
#SPJ8
Okie help help math math math

Answers
Answer:
\(\displaystyle y = -3x + 9\)
Step-by-step explanation:
First, find the rate of change of the line:
\(\displaystyle \frac{-y_1 + y_2}{-x_1 + x_2} = m \\ \\ \frac{-6 + 3}{-1 + 2} = m \hookrightarrow \frac{-3}{1} = m \\ \\ \boxed{-3 = m}\)
_______________________________________________
Now plug all the information into the Slope-Intercept Formula. It does not matter which ordered pair is chosen:
\(\displaystyle 3 = -3[2] + b \hookrightarrow 3 = -6 + b; 9 = b \\ \\ \boxed{\boxed{y = -3x + 9}} \\ \\ OR \\ \\ 6 = -3[1] + b \hookrightarrow 6 = -3 + b; 9 = b \\ \\ \boxed{\boxed{y = -3x + 9}}\)
I am joyous to assist you at any time.
Which function has a greater rate of change? Which function has the greater y-intercept?
Explain how you know.

Answers
Answer:
Function B
Step-by-step explanation:
Using any two pairs from the table of values given, say, (0, 1) and (4, 2):
Rate of change =
Rate of change for function A = ¼ = 0.25
✍️Rate of change for Function B:
Equation for Function B is given in the slope-intercept format, y = mx + b.
m = slope = rate of change.
Therefore, the function, y = 0.75x - 2 has a rate of change of 0.75.
Rate of change of Function B = 0.75.
✅0.75 if greater than 0.25, therefore, Function B has the greater rate of change.
what's the answer tell me what the equation is and I have 2 other questions if u can help we with another one of these too

Answers
Answer:
1/5 and 5/5
Step-by-step explanation:
Select all the expressions that are equivalent to 7(2−3).
Answers
Answer:
7(2-3) = -7
Step-by-step explanation:
Hope this helps, but you did not give us any options to choose from.
Predict the shape of the molecule.
2-
S
:0:
A. linear
B. trigonal planar
C. tetrahedral
D. bent

Answers
Answer:c
Step-by-step explanation:
Write the word sentence as an equation. Then solve.
Five more than a number c is −9.
Answers
Step-by-step explanation:
So we are given that the number we are looking for is \(c\). The problem says, "five more than a number". So, \(c+5\). 'Is' typically means equals.
\(c+5=-9\)
Then we can solve for \(c\).
\(c+5=-9\\c=-14\)
Hope this helps!
What's the sum of ⅖ and ¾? О A. % • в. ⅐ • C. % O D. 1%0
Answers
22. How many positive integers less than 1000 a) are divisible by 7? b) are divisible by 7 but not by 11? c) are divisible by both 7 and 11? d) are divisible by either 7 or 11? e) are divisible by exactly one of 7 and 11? f ) are divisible by neither 7 nor 11? g) have distinct digits? h) have distinct digits and are even?
Answers
The set of positive integers less than 1000 that are:
a)Divisible by 7 are 142
b)Divisible by 7 but not by 11 are 130
c)Divisible by both 7 and 11 are 12
d)Divisible by either 7 or 11 are 220
e)Divisible by exactly one of 7 and 11 are 220
f)Divisible by neither 7 nor 11 are 780
g)Having distinct digits are 576
h)Having distinct digits and even are 337
We have,
A whole number that is greater than zero is known as positive integer
a)The positive numbers below 1000 that are divisible by 7 are 7, 14, 21, 28,..., 994.
Total terms: 994, divided by 7, plus (n-1)
There are 142 total terms below 1000 that are divisible by 7.
b) The numbers 77, 154, 231, 308, 385, 462, 539, 616, 693, 770, 847, and 924 are all divisible by both 7 and 11.
The total number of integers below 1000 that are divisible by 7 but not 11 therefore equals 142 - (total number of integers divisible by 7 and 11), which means that the total number of integers that fall into this category is 130.
c) The total amount of integers that can be divided by both 7 and 11 equals the total amount of integers that can be divided by 77.
There are 12 total integers below 1000 that can be divided by 77.
d) The total number of integers that can be divided by either 7 or 11 is equal to the sum of the numbers that can be divided by each of those numbers and the number that can be divided by 77.
The total number of integers below 1000 that are divisible by 11 is (11,22,33,...,990). 990 = 11 + (n-1) 11, which equals 90 integers.
Total integers that may be divided by both 7 and 11 are equal to 142 + 90 - 12 = 220.
e) The total number of integers that may be divided by either 7 or 11 perfectly is equal to 142 + 90 - 12 = 220 numbers.
f) The total number of integers that cannot be divided by either 7 or 11 is 1000 - (The total number of integers that can be divided by either 7 or 11), which is 1000 - 220 = 780 numbers.
g)Distinct digits from 1 to 100 = 100 - Total number of integers below 1000 with distinct digits = 1000 - (non-distinct digits) ( 11,22,33,44,55,66,77,88,99,100),
=> Unique digits from 1 to 100 equal 90.
=> The distinct numerals 101 to 200 equal 100. (101,110,111,112,113,114,115,116,117,118,119,121,122,131,133,141,144,151,155,161,166,171,177,181,188,191,199,200),
=> Unique digits from 101 to 200 are: 100 to 28, 72.
=> Unique numbers between 201 and 1000 = 72 x 8 = 576.
h)Different digits and even values equal to 337
To know more about positive integers, visit:
brainly.com/question/13733829
#SPJ1