Use the logarithm lays to simplify this expression
log2 8x^3/2 = log2 8x^3 - log2 2y
Answers
By applying logarithm laws and the relationship between logarithms and powers of same base, the expression \(\log_{2} \frac{8\cdot x^{3}}{2} = \log_{2} 8\cdot x^{3} - \log_{2} 2\cdot y\) is equal to y = 1.
How to simplify a logarithmic expressions
Herein we must simplify an expression that uses logarithms by applying any of the following three laws:
\(\log_{a} (b \cdot c) = \log_{a} b + \log_{a} c\) (1)
\(\log_{a} \left(\frac{b}{c} \right) = \log_{a} b - \log_{a} c\) (2)
\(\log_{a}{b^{c}} = c \cdot \log_{a} b\) (3)
Now we proceed to simplify the expression:
\(\log_{2} \frac{8\cdot x^{3}}{2} = \log_{2} 8\cdot x^{3} - \log_{2} 2\cdot y\)
\(\log_{2} 2\cdot y = \log_{2} 8\cdot x^{3} - \log_{2} \frac{8\cdot x^{3}}{2}\)
\(\log_{2} 2 \cdot y = \log_{2} \frac{\frac{8\cdot x^{3}}{1} }{\frac{8\cdot x^{3}}{2} }\)
\(\log_{2} 2\cdot y = \log_{2} 2\)
By the relationship between logarithms and powers of same base:
2 · y = 2
y = 1
By applying logarithm laws and the relationship between logarithms and powers of same base, the expression \(\log_{2} \frac{8\cdot x^{3}}{2} = \log_{2} 8\cdot x^{3} - \log_{2} 2\cdot y\) is equal to y = 1.
To learn more on logarithms: https://brainly.com/question/20785664
#SPJ1
Related Questions
Complete the sentence to describe the triangle shown with two answers
A. Acute triangle
B. Obtuse triangle
C. A right angle
AND
A. Equilateral triangle
B. A isosceles triangle
C. Scalene triangle

Answers
and
B) Isosceles triangle
If a wedding ring is dropped from a tall building, the distance it has fallen in feet is given by 16t2, where t is the time in seconds since the ring was dropped. How far has the ring fallen after 5 seconds?
Answers
8)
Solve: 5x - 7x + 6 = -2(x - 3).
0)
A)
0
B)
2
infinitely many solutions
Answers
Answer:
the answer is 0 because both equations on either side cancel out thereby leaving in bare
Which algebraic expression represents the phrase “seven more than half of a number”?
7 minus one-half x
Negative 7 + one-half x
One-half x + 7
Negative one-half x minus 7
Answers
Answer:
C: 1/2x +7
Step-by-step explanation:
8 decreased by the difference of t and 4
Answers
Answer:
See below.
Step-by-step explanation:
(t-4)-8
Remove parenthesis.
t-4-8
Combine like terms.
t-12
-hope it helps
PLEASE HELP!!! Solve 5sin(π/3x)=3 for the four smallest positive solutions
Answers
This one's a special case of a right angled triangle with sides (3, 4, and 5 units)
Back to the problem :\(\qquad\displaystyle \tt \dashrightarrow \: 5 \sin \bigg( \frac{ \pi}{3} x \bigg) = 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \frac{3}{5} \)
Now, check the triangle, sin 37° = 3/5
therefore,
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \sin(37 \degree) \)
[ convert degrees on right side to radians ]
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \sin \bigg(37 \degree \times \frac{ \pi}{180 \degree} \bigg ) \)
There are three more possible values as :
\(\qquad\displaystyle \tt \dashrightarrow \: \sin( \theta) = \sin(\pi - \theta) \)
\(\qquad\displaystyle \tt \dashrightarrow \: sin( \theta) = \sin \bigg( { 2\pi}{} + \theta \bigg) \)
\(\qquad\displaystyle \tt \dashrightarrow \: sin( \theta) = \sin \bigg( \frac{ 3\pi}{} - \theta\bigg) \)
Equating both, we get : First value :\(\qquad\displaystyle \tt \dashrightarrow \: \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 37 \times \frac{ \cancel \pi}{180} \times \frac{3}{ \cancel \pi} \)
\(\qquad\displaystyle \tt \dashrightarrow \: x = \frac{37}{60} \)
or in decimals :
\(\qquad\displaystyle \tt \dashrightarrow \: x = 0.616666... = 0.6167\)
[ 6 repeats at third place after decimal, till four decimal places it would be 0.6167 after rounding off ]
similarly,
Second value :\(\qquad\displaystyle \tt \dashrightarrow \: \pi - \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(1 - \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 1 - \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: - \frac{x}{3} = 0.205 - 1\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 0.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times 0.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 2.385\)
Third value :\(\qquad\displaystyle \tt \dashrightarrow \: 2\pi + \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(2 + \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 2 + \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 0.205 - 2\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = - 1.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times -1 .795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = -5.385\)
Fourth value :\(\qquad\displaystyle \tt \dashrightarrow \: 3 \pi - \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(3 - \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 3 - \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: - \frac{x}{3} = 0.205 - 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 2.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times 2.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 8.385\)
" x can have infinite number of values here with the same result, here are the four values as you requested "
I hope it was helpful ~

Shawna went shopping at the thrift store yesterday and came home with 12 items and she only spent $31.50. She only got shirts and pants. If each shirt cost $2 and each pair of pants cost $3.50, which system of equations would represent this situation?
Answers
2y+3.50x=31.50 and 2y= 31.50-3.50x
I hope this helps you out!
Use a calculator to find the trigonometric ratio. Round your answer to four decimal places
sin 98°~
Answers
Using a calculator, the trigonometric ratio of sin 98 is approximately 0.9848.
How to Find the Trigonometric Ratio?One of the trigonometric ratio we have in mathematics is the sine ratio. We can use calculator to find the sine of an angle without making use of tables. To do this on your calculator, enter the sine function followed by the degree of the angle you want to find its sine. You will get your answer.
Using a calculator, we can find the sine of 98 degrees as follows:
sin 98° ≈ 0.9848
Rounding this to four decimal places, we get:
sin 98° ≈ 0.9848
Therefore, sin 98° is approximately equal to 0.9848.
Learn more about trigonometric ratio on:
https://brainly.com/question/10417664
#SPJ1
(03.02 MC)
Which of the following is a factor of 12x2 − 4x − 1? (6 points)
Group of answer choices
A. 6x − 1
B. 2x + 1
C. 2x − 1
D. None of the above
Answers
Answer:
C
Step-by-step explanation:
Using the integers −9 to 9 at most one time each, place a digit in each box ( ___ , ____) and. ( ___ , ____) to create endpoints for the longest possible line segment both numerically and graphically whose midpoint is (1, 3)
Answers
Using the integers −9 to 9 at most one time each, place a digit in each box (1, 3) and (9, 3) or (-9, 3) to create endpoints for the longest possible line segment both numerically and graphically whose midpoint is (1, 3).
To find the endpoints of the longest possible line segment with midpoint (1, 3), we can use the midpoint formula, which states that the midpoint of a line segment with endpoints (x₁, y₁) and (x₂, y₂) is ((x₁+x₂)/2, (y₁+y₂)/2).
In this case, we know the midpoint is (1, 3), so we can set up two equations using the variables for the endpoints (x and y) and solve for them:
(x₁ + x₂)/2 = 1
(y₁ + y₂)/2 = 3
We also know that the line segment must be as long as possible, so the endpoints should be as far away from each other as possible. To maximize the distance between the endpoints, we can choose one endpoint to be -9 and the other endpoint to be 9. This gives us:
(x₁ + x₂)/2 = 1 => x₁ + x₂ = 2
(y₁ + y₂)/2 = 3 => y₁ + y₂ = 6
Now we can solve for x₁ and y₁, since x₂ and y₂ will be 2-x₁ and 6-y₁ respectively:
x₁ + (2-x₁) = 2 => x₁ = 1
y₁ + (6-y₁) = 6 => y₁ = 3
So the endpoints of the longest possible line segment with midpoint (1, 3) are (1, 3) and (9, 3) or (-9, 3), and its length is 8 units.
To learn more about midpoint click on,
https://brainly.com/question/12885634
#SPJ1
i need help with this question!!!!!!

Answers
Answer: \(87^{\circ}\)
Step-by-step explanation:
Because an angle inscribed in a semicircle is a right angle, \(\angle B=90^{\circ}\)
So, as angles in a triangle add to 180 degrees, \(\angle A=180^{\circ}-90^{\circ}-3^{\circ}=\boxed{87^{\circ}}\)
The manager of a new supermarket wished to estimate the likely expenditure of his customers. A sample of till slips from a similar supermarket describing the weekly amount spent by 500 randomly selected customers was collected and analysed. This expenditure was found to be approximately normally distributed with a mean of $50 and a standard deviation of $15.
Find the probability that any shopper selected at random spends more than $80 per week?
Find the percentage of shoppers who are expected to spend between $30 and 80 per week?
Answers
Answer:
0.0228 = 2.28% probability that any shopper selected at random spends more than $80 per week.
88.54% of shoppers are expected to spend between $30 and 80 per week.
Step-by-step explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Normally distributed with a mean of $50 and a standard deviation of $15.
This means that \(\mu = 50, \sigma = 15\)
Find the probability that any shopper selected at random spends more than $80 per week?
This is 1 subtracted by the p-value of Z when X = 80. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{80 - 50}{15}\)
\(Z = 2\)
\(Z = 2\) has a p-value of 0.9772
1 - 0.9772 = 0.0228
0.0228 = 2.28% probability that any shopper selected at random spends more than $80 per week.
Find the percentage of shoppers who are expected to spend between $30 and 80 per week?
The proportion is the p-value of Z when X = 80 subtracted by the p-value of Z when X = 30.
X = 80
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{80 - 50}{15}\)
\(Z = 2\)
\(Z = 2\) has a p-value of 0.9772
X = 30
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{30 - 50}{15}\)
\(Z = -1.33\)
\(Z = -1.33\) has a p-value of 0.0918
0.9772 - 0.0918 = 0.8854
0.8854*100% = 88.54%
88.54% of shoppers are expected to spend between $30 and 80 per week.
PLZ HELP THANK YOU BRAINLIEST IF CORRECT select all that apply (look at the photo)

Answers
150/20 is 7.5
if you divide these options by each other you’ll 7.5 which means they’re equal :)
Ellie shares 24 cupcakes with x friends, how many cupcakes does each friend get?
Answers
Answer:
24/ 1 + x
you would have to divide the cupcakes upon the friends.
X is normally distributed random variable with mean 72 and standard deviation 22.
Answers
Therefore , X is a continuous random variable, the probability of getting exactly X = 80 is zero. We can only find the probability of a range of values, such as P(79.5 < X < 80.5).
What exactly does the probability method suggest?Calculating the likelihood that a statement is true or that a particular event will take place is the centre of probability theory, a branch of mathematics. Any number between range 0 and 1, where 1 is usually used to express confidence as well as 0 is routinely used it to convey possibility, can be used to represent chance. A probability diagram shows the likelihood that a particular occurrence will occur.
Here,
For P(78 < X < 127):
We first convert the values to standard scores:
Z1 = (78 - 72) / 22 = 0.27
Z2 = (127 - 72) / 22 = 2.50
Using a standard normal distribution table or a calculator, we find the area to the left of Z1 and the area to the left of Z2:
P(Z < 0.27) = 0.6064
P(Z < 2.50) = 0.9938
Then we subtract the smaller area from the larger area to find the area between Z1 and Z2:
P(0.27 < Z < 2.50) = 0.9938 - 0.6064 = 0.3874
So the probability that 78 < X < 127 is approximately 0.3874.
For P(60 < X < 90):
We first convert the values to standard scores:
Z1 = (60 - 72) / 22 = -0.55
Z2 = (90 - 72) / 22 = 0.82
Using a standard normal distribution table or a calculator, we find the area to the left of Z1 and the area to the left of Z2:
P(Z < -0.55) = 0.2912
P(Z < 0.82) = 0.7939
Then we subtract the smaller area from the larger area to find the area between Z1 and Z2:
P(-0.55 < Z < 0.82) = 0.7939 - 0.2912 = 0.5027
So the probability that 60 < X < 90 is approximately 0.5027.
For P(X = 80):
Since X is a continuous random variable, the probability of getting exactly X = 80 is zero. We can only find the probability of a range of values, such as P(79.5 < X < 80.5).
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
The complete question is " X Is A Normally Distributed Random Variable With Mean 72 And Standard Deviation 22. Use Calculator To Find The Probability Indicated. P(78≪X≪127) P(60≪X≪90) P(X=80)
X is a normally distributed random variable with mean 72 and standard deviation 22. Use calculator to find the probability indicated.
P(78<X<127)
P(60<X<90)
P(X=80)"
What additional information would allow you to prove the quadrilateral is a parallelogram according to the minimum criteria?
Question 5 options:
A)
||
B)
≅
C)
≅
D)
∠F ≅ ∠H

Answers
The additional information would allow you to prove the quadrilateral is a parallelogram according to the minimum criteria is
EJ ≅ GJ. Option A
How to prove the statementWe need to know the properties of a parallelogram, we have;
Opposite sides are parallel.Opposite sides are congruent.Opposite angles are congruent.Same-Side interior angles (consecutive angles) are supplementary.We know that FJ ≅ JH, it's given by the marks, now if it were to happen that EJ ≅ GJ, that would mean that the diagonals on that quadrilateral are bisecting each other, and if that's so, then the quadrilateral it's indeed a parallelogram.
Learn more about quadrilaterals at: https://brainly.com/question/23935806
#SPJ1
The complete question:
What additional information would allow you to prove the quadrilateral is a parallelogram according to the minimum criteria?
A)
ej ≅ gj
B)
ej || gj
C)
fg || eh
D)
ef ≅ hg
You spinner that has 12 equal sides sections number 1 through 12 find each probability probability three or four
Answers
Answer:
1 in 12 chance of landing on 3
1 in 12 chance of landing on 4
1 in 6 chance of landing on either 3 or 4
Step-by-step explanation:
12 equal sections means probability is 1 in 12 of landing on any one numbered section.
2 in 12 or 1 in 6 chance of landing on either of two numbered sections in one attempt.
A rectangle has an area of 189 m2 and the length of 21m. What is it’s width?
Answers
Answer:
9 meters
Step-by-step explanation:
189 divided by 21 is 9 (:
Answer:
9m
Step-by-step explanation:
To find the width of a rectangle given area and length all you need to do is take your area (189 in this case) and divide it by your length. (In this case 21.)
Here's our equation:
189 ÷ 21 = 9
(remember the meters squared is important if you're finding area. This doesn't apply in our case as we're only finding the width. To be more clear the "m² and/or m^2")
9m is your answer.
Hope this helps and have a nice day!
SOMEONE PLEASE ANSWER. I'M CRYING AND DONT KNOW WHAT TO DO! I NEED YOUR HELP PLEASE!
A cafeteria serves lemonade that is made from a powdered drink mix. There is a proportional relationship between the number of scoops of powdered drink mix and the amount of water needed to make it. For every 2 scoops of mix, one half gallon of water is needed, and for every 5 scoops of mix, one and one fourth gallons of water are needed. Part A: Find the constant of proportionality. Show every step of your work. Part B: Write an equation that represents the relationship. Show every step of your work. Part C: Describe how you would graph the relationship. Use complete sentences. Part D: How many gallons of water are needed for 12 scoops of drink mix?
Answers
Below, you'll find a list of all the answers to the questions which are solved by using proportional relationship.
What is the fundamental formula for a straight line?The general equation for a straight line is y=mx + c, where m represents the line's slope and expresses the rate of change of y per unit time with respect to x.
The point where the graph crosses the y-axis is called the y-intercept, or c.
Direct proportionality is also represented by y = mx. We can express m as follows: m = y/x
OR
y₁/x₁ = y₂/x₂
In our cafeteria, lemonade is made using a powdered drink mix. The quantity of water required to manufacture a certain amount of powdered drink mix is proportional to the number of scoops required. For every 2 scoops of mix, 1/2 gallon of water is required, and for every 5 scoops,
1 1/4 gallons of water are required.
The proportional formula is written as y = k x.
Using the information provided, we can now write: 2 scoops require 0.5 gallon of water.
1.25 gallon of water is required for 6 scoops.
This means that k = 2/0.5
k = 2/(1/2)
k = 2 x 2
k= 4
Equations describing the relationship can be expressed as y = 4x + c.
0.5 gallon of water is now required for 2 scoops.
2=4(1/2)+c
2=2+c
c=0
Therefore, the formula will be y = 4x.
The end includes a graph for y = 4x.
12 scoops of water:
12=4x
x=3 gallons of water is needed.
To know more about proportional relationship, visit:
https://brainly.com/question/29765554
#SPJ1

Could someone help me out with this question?

Answers
The simplified form of the difference quotient of equation \(9x^2+5x-1\) . in the form 9x + 9h + 5.
In question for equation \(9x^2+5x-1\), simplified to difference quotient in the form of Ax+Bh+C where A, B, C are integers
equation is the relationship between variable and represented as \(9x^2+5x-1\) is example of polynomial equation.
We know that,
for difference quotient
\(=\frac{f(x+h)-f(x)}{h} \\\frac{9(x+h)^2+5(x+h)-1-9x^2-5x+1}{h}\\\frac{9h^2+9hx+5h}{h}\\9x+9h+5\)
While, compared with Ax+Bh+C
we have A=9, B=9, C=5.
Thus, The required value of difference Quotient in the form Ax+Bh+c where A, B and C is 9, 9 and 5 respectively
Learn more about equation here:
https://brainly.com/question/10413253
#SPJ1
Goose a variable and write an equation to solve the situation. Kevin drive 320 miles to a mountain resort. His return trip took 20 minutes longer because his speed returning was 4 mr/h slower than his speed going.
Answers
Answer:
320/x + 1/3 = 320/(x - 4) x = 64 mphStep-by-step explanation:
Let the speed is x.
We have equation:
320/x + 20/60 = 320/(x - 4) ⇒ 320/x + 1/3 = 320/(x - 4)To solve we need to get rid of fraction:
320(x - 4) + 1/3x(x - 4) = 320xx² - 4x - 3840 = 0x² - 4x + 4 = 3844(x - 2)² = 62²x - 2 = 62x = 64MATH
Systems of Linear Equations
1. Determine if each system of equations below is linear or nonlinear.
A. -9x+8y = 9x 7y+8=8x
Linear or nonlinear?
D. 6y+x=12 y-x=1-x
B.
2.3y+1.2x = 0
1.1x+0.1y 1.2
C.
2 7-3y=- 2x+9= 3y
Linear or nonlinear?
Linear or nonlinear?
E. 45x + y = 12 y+x² = 1-x²
Linear or nonlinear?
G
0.2x+9.1y9.1√x
7x+1=8√y
Linear or nonlinear?
F. x+8y = 81 x-7y = 32
Linear or nonlinear?
H.
98317y= 1010 + 2965x
-71389y=5692x - 1001
3 xx y-5= 1 zy+3x=-21
Linear or nonlinear?
Linear or nonlinear?
Linear or nonlinear?
2. Find the solution, if one exists, for each of the graphs shown below that are representing different systems of linear equations.
A.
B.
Solution:
Solution:
C.
D.
Solution:
Solution:
2. Find the solution, if one exists, for each of the graphs shown below that are representing different systems of linear equations.
A.
B.
Solution:
Solution:
C.
D.
Solution:
Solution:


Answers
The system of equations -9x+8y = 9x and 7y+8=8x is linear.
A system of equations is considered linear if each equation in the system is linear, meaning that the highest power of any variable in each equation is 1.
In this case, the first equation -9x+8y = 9x is linear because the highest power of any variable is 1 (x is raised to the first power).
Similarly, the second equation 7y+8=8x is also linear because the highest power of any variable is 1 (x is raised to the first power and y is not raised to any power).
Therefore, the system of equations is linear.
Learn more about the System of equations here:
https://brainly.com/question/12628931
#SPJ1
f(x)=2x-6 g(x)=3x+9, find (f+g)
Answers
Answer:
(f+g)(x) = 5x +3
Step-by-step explanation:
(f+g)(x) = f(x) +g(x)
= (2x -6) +(3x +9)
= 2x +3x -6 +9
(f+g)(x) = 5x +3
El mayor es Novecientos mil cuatrocientos ochenta y nueve , y cuarenta mil dos
Answers
El número "Novecientos mil cuatrocientos ochenta y nueve" se representa como 900,489 en notación numérica.
Por otro lado, el número "cuarenta mil dos" se representa como 40,002.
Si estamos buscando determinar cuál de estos dos números es mayor, podemos comparar las cifras en cada posición.
Comenzando desde la izquierda, el primer dígito de 900,489 es 9, mientras que el primer dígito de 40,002 es 4.
Dado que 9 es mayor que 4, podemos concluir que 900,489 es mayor que 40,002.
En general, al comparar números, se debe observar cada posición en orden de mayor a menor importancia.
Esto significa que el primer dígito a la izquierda es el más significativo y tiene más peso en el valor total del número.
Si los dígitos en la posición más significativa son iguales, se debe pasar a la siguiente posición hasta que se encuentre una diferencia.
En este caso, dado que el primer dígito de 900,489 es mayor que el primer dígito de 40,002, no es necesario comparar los dígitos en posiciones posteriores.
Por lo tanto, podemos concluir que el número "Novecientos mil cuatrocientos ochenta y nueve" (900,489) es mayor que "cuarenta mil dos" (40,002).
For similar questions on Novecientos
https://brainly.com/question/1753221
#SPJ8
on the first one shows you how to solve it then second one is the problem just tell me the answer pls have a good day bye

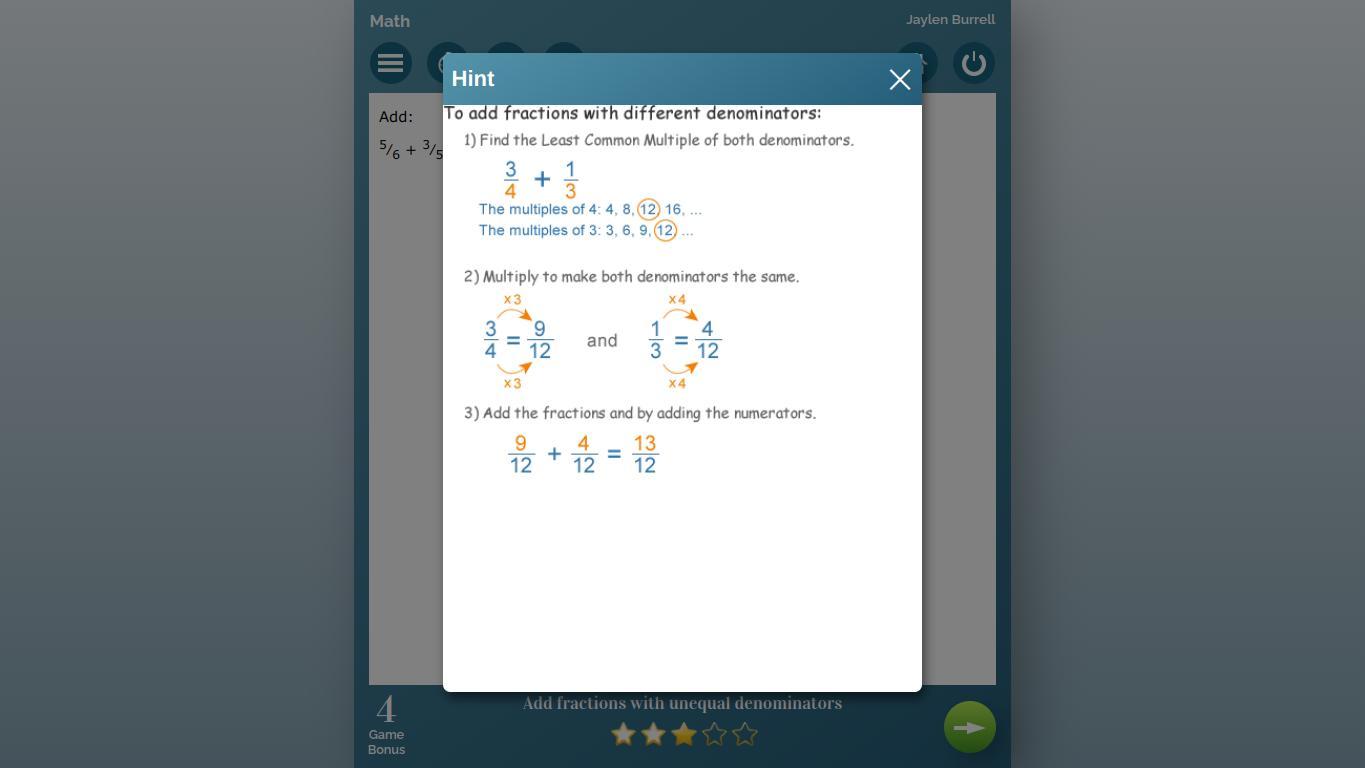
Answers
Answer:
43/30
Step-by-step explanation:
Answer:
1 13/30
Step-by-step explanation:
6 & 5 have a Lcm of 30, so lets use that for our denominator so we can add.
5/6 + 3/5 = 25/30 + 18/30
=
43/30 which is equal to 1 13/30.
If you were to use the substitution method to solve the following system, choose the new equation after the expression equivalent to y from the first equation is substituted into the second equation. 12x − y = −4 4x − 3y = −6 a 4x − 3(−12x − 4) = −6 b 4x − 3(12x + 4) = −6 c 4(12x + 4) − 3y = −6 d 4(−12x − 4) − 3y = −6
Answers
Step-by-step explanation:
Sand Timer Volume Calculation
Puranik Dewangan
need an explanation
It takes 15 minutes for all of the sand to flow through a sand timer. The sand timer contains 475 grams of sand. Each millilitre of sand weighs 1.5 grams. How many millilitres of sand flow through the timer per minute?
To solve the problem, we need to find the total volume of sand that flows through the timer in 15 minutes, and then divide it by 15 to find the volume per minute.
First, let's find the total weight of the sand in grams:
475 grams
Next, we can convert the weight to volume by dividing by the weight of one milliliter of sand:
475 grams ÷ 1.5 grams/mL = 316.67 mL
So 316.67 mL of sand flows through the timer in 15 minutes. To find the volume per minute, we divide by 15:
316.67 mL ÷ 15 minutes = 21.11 mL/minute
Therefore, 21.11 millilitres of sand flow through the timer per minute.
Puranik Dewangan
If you were to use the substitution method to solve the following system, choose the new equation after the expression equivalent to y from the first equation is substituted into the second equation. 12x − y = −4 4x − 3y = −6 a 4x − 3(−12x − 4) = −6 b 4x − 3(12x + 4) = −6 c 4(12x + 4) − 3y = −6 d 4(−12x − 4) − 3y = −6
To use the substitution method, we need to solve one of the equations for one of the variables in terms of the other variable, and then substitute the resulting expression into the other equation. In this case, we can solve the first equation for y:
12x - y = -4
y = 12x + 4
Now we can substitute this expression for y into the second equation:
4x - 3y = -6
4x - 3(12x + 4) = -6
Simplifying this equation gives:
4x - 36x - 12 = -6
-32x = 6
x = -6/32 = -3/16
Now we can substitute this value of x back into either of the original equations to find y. Let's use the first equation:
12x - y = -4
12(-3/16) - y = -4
-27/4 = y
So the solution to the system is (x, y) = (-3/16, -27/4).
Therefore, the answer to the given question is (b) 4x − 3(12x + 4) = −6, which is the second equation after the substitution of y = 12x + 4.
y=3/4x-1/2 in a graph
Answers
Answer:
Look at the graph below, hope this helped :)
Step-by-step explanation:

The Unemployment Rate is calculated by
taking the number of unemployed
people and dividing it by the working
labor force. What is the unemployment
rate if the labor force is 90 people and 6
are unemployed?
A 8.3%
B. 6.7%
C. 5.8%
Answers
The unemployment rate is 6.7%.
The correct option is B.
How do I calculate the percentage?The following formula is a general strategy for calculating percentages.
Finds the total amount of what you are searching for as a percentage. ...
Divide the number to get the percentage.
Multiply the value by 100. In mathematics, a percentage is a number or ratio expressed as a fraction of 100. Often indicated by the percent sign "%", the abbreviations "pct.", "Pct", and in some cases, "pc" is also used. Percentages are dimensionless.
There is no measurement unit. Multiply the number of integers by the decimal number that corresponds to the percentage. The result is the percentage of shares.
explanation;
total people =90
unemployment = 6
percentage = 6*100/90
6.7%.
Learn more about percentages here: https://brainly.com/question/251701
#SPJ2
Show the algorithm/abstract strategy to justify the 3/5?
Answers
The algorithm/abstract strategy to justify the fraction 3/5 involves interpreting it as a division, performing the division, and obtaining the decimal representation as the results.
To justify the fraction 3/5, we can use the concept of division and understand it as a ratio or proportion.
Algorithm/Abstract Strategy:
Start with the numerator, which is 3.
Identify the denominator, which is 5.
Interpret the fraction as a ratio or comparison between the numerator and denominator.
Understand that 3/5 represents a division where the numerator (3) is divided by the denominator (5).
Perform the division: 3 ÷ 5.
Simplify the division to its simplest form, if necessary.
The result of the division, in this case, is the decimal representation of the fraction.
If required, convert the decimal representation to a percentage or any other desired form.
For example, if we perform the division 3 ÷ 5, the result is 0.6.
So, 3/5 can be justified as the ratio or proportion where the numerator (3) is divided by the denominator (5) resulting in 0.6.
For similar question on algorithm/abstract strategy.
https://brainly.com/question/31332020
#SPJ8
A cyclist rides his bike at a rate of 30 kilometers per hour. What is this rate in miles per hour? How many miles will the cyclist travel in 3 hours? In your computations, assume that 1 mile is equal to 1.6 kilometers. Do not round your answers.
Answers
Answer:4.8
Step-by-step explanation:
30/3 x 1.6