Translate into a variable expression. (Use x for your variable.) the sum of six sevenths of a number and three Need Help? Read it Watch Submit Answer
Answers
The variable expression that represents the sum of six sevenths of a number and three is (6/7)x + 3.
In this expression, "x" represents the unknown number. The term "6/7x" represents six sevenths of the number, indicating that the number is multiplied by six sevenths. The term "3" represents the constant value of three.
When these two terms are added together, we obtain the sum of six sevenths of the number and three. This variable expression allows us to represent mathematically the given phrase and can be used to evaluate or manipulate equations involving the sum of six sevenths of a number and three.
To learn more about variable expression click here: brainly.com/question/1511425
#SPJ11
Related Questions
Help explain how to solve

Answers
The value of the angle U in the triangle is 92.10 degrees.
How to find the angle in a triangle?The angle U in the triangle can be found using cosine rule as follows:
Let's use cosine formula to find the angle U
c² = a² + b² - 2ab cos C
Hence,
Therefore,
a = 58.8
b = 38.4
c = 71.4
Hence,
71.4² = 58.8² + 38.4² - 2(58.8)(38.4) cos U
5097.96 = 3457.44 + 1474.56 - 4515.84 cos U
5097.96 - 4932 = - 4515.84 cos U
165.96 = - 4515.84 cos U
divide both sides by - 4515.84
cos U = 165.96 / - 4515.84
cos U = - 0.03675063775
U = cos⁻¹ - 0.03675063775
U = 92.1032274244
Therefore,
U = 92.10 degrees
learn more on triangle here: https://brainly.com/question/28855901
#SPJ1
In 3–5 sentences, explain why the moon appears to be less bright than the sun despite its very close distance to Earth. PLEASE HELP A GIRL OUT THIS IS A VERY IMPORTANT TEST I DO NOT WANT TO FAIL make it simple
Answers
Step-by-step explanation:
Based on scientific observations and findings, the reasons the moon appears to be less bright than the sun despite its very close distance to earth are the following:
Moon doesn't produce its light but rather takes or reflects the light from the Sun.
Moon only reflects about 12 percent maximum of lights that shines on it from the sun.
Externally, Moon is made of dark-colored soil often referred to as lunar soil. This is unlike the Sun which is made of hydrogen and helium, whose atoms are very light.
Also, Sun is about 400 times bigger than the Moon.
Hence, in this case, it is concluded that there are many reasons the moon appears to be less bright than the sun despite its very close distance to earth.
Graph the function g(x)= 1/4x+4
Answers
The given function is
\(g(x)=\frac{1}{4}x+4\)First, we make x = 0.
\(g(0)=\frac{1}{4}\cdot0+4=0+4=4\)Second, we make g(x) = 0.
\(\begin{gathered} 0=\frac{1}{4}x+4 \\ -4=\frac{1}{4}x \\ x=-16 \end{gathered}\)Third, we graph the points (0, 4) and (-16, 0).
At last, we draw the line through the points to get the line.


The difference of x and y is 14. The value of x is 3 more than
twice the value of y. Write two equations and graph to find
the value of x.
O X = 25
O x = -17
OX= 4
O x = 11
Answers
The value of X = 25.
The difference of x and y is 14. The value of x is 3 more thantwice the value of y. Find the value of x and y.Solution:
The two equations are
(i) the first condition is difference of x and y is 14
x - y = 14 ---------equation 1
(ii) the second condition of the given data is value of x is 3 times more than two times of y value.
x - 2y = 3 --------equation 2
From equation 2, we have to separate two variables x and y,
x = 3 + 2y --------equation 3
We have to Substitute equation 3 in equation 1
3 + 2y - y = 14
3 + y = 14
y = 14 - 3
y = 11
Substitute y = 11 in equation 1........
x - 11 = 14
x = 14 + 11
x = 25
So, the value of x is 25 and y is 11.
To learn more about equations refer to:
https://brainly.com/question/2972832
#SPJ1
Answer:
x - y = 14x - 2y = 3x = 25Step-by-step explanation:
Given the difference of x and y is 14, and the difference of x and 2y is 3, you want two equations, their graph, and the value of x.
EquationsThe difference of 'a' and 'b' is (a -b). Here, the two differences are expressed as the equations ...
x - y = 14x - 2y = 3GraphThe attachment shows a graph of these equations. Their point of intersection is (25, 11), meaning the value of x is 25.
The graph of the first equation is easily drawn by recognizing the x- and y-intercepts are 14 and -14, respectively.
The graph of the second equation will go through the x-intercept point of (3, 0) and the y-intercept point of (0, -3/2). It is probably easier to graph this by hand by considering the x-intercept point and the slope of 1/2.
Algebraic solutionSince we're only interested in the value of x, it is convenient to eliminate the variable y. We can to that by subtracting the second equation from twice the first:
2(x -y) -(x -2y) = 2(14) -(3)
x = 25 . . . . . . . . . simplify

Tavon has a gift card of $90 that loses $2 for each 30-day period not used. He has another gift card for $70 that loses $1.50 for each 30-day period not used. What will the value of each card be when they have equal value?
Answers
Answer:
$10
Step-by-step explanation:
Let the number of 30 day periods be x.
\(90-2x=70-1.5x \\ \\ 20=0.5x \\ \\ x=40\)
When x=40, the value is 90-2(40)=$10.
The value of each card will be $ 10 after 40 periods, where the value of the first and second cards are equal.
Given data:
Let x represent the number of 30-day periods that have passed since the gift cards were obtained.
For the first gift card with $90 initial value and losing $2 for each 30-day period:
Value of the first card = Initial value - Loss per period * Number of periods
Value of the first card = $90 - $2 * x
For the second gift card with $70 initial value and losing $1.50 for each 30-day period:
Value of the second card = Initial value - Loss per period * Number of periods
Value of the second card = $70 - $1.50 * x
Now, to find when the two cards have equal value x:
Value of the first card = Value of the second card
$90 - $2 * x = $70 - $1.50 * x
On simplifying the equation:
$90 - $70 = $2 * x - $1.50 * x
$20 = $0.50 * x
x = $20 / $0.50
x = 40
After 40 periods of 30 days each, the two cards will have equal value.
Now, determine the value of each card at this point:
Value of the first card = $90 - $2 * 40 = $90 - $80 = $10
Value of the second card = $70 - $1.50 * 40 = $70 - $60 = $10
Hence, both cards will have a value of $10 when they have equal value after 40 periods.
To learn more about equations, refer:
https://brainly.com/question/19297665
#SPJ3
8. Two bicycle trails were developed in a new housing development. One trail is 3 miles long. The
other trail is as long. How long is the second trail?
G
2 miles
2 miles
3
H 2 miles
14 55
N
miles
Answers
Based on the given information, we know that one bicycle trail in a new housing development is 3 miles long and the other trail is the same length as the first trail.
Therefore, the length of the second trail is also 3 miles.
Hence, the answer is: 3 miles
It seems like there's a missing piece of information in your question about the length of the second trail.
However, I will try my best to help you with the given information.
Two bicycle trails are developed in the housing development.
The first trail is 3 miles long, and we need to find the length of the second trail.
Unfortunately, there is no information provided about the second trail's length.
For similar question on bicycle trail.
https://brainly.com/question/30963648
#SPJ11
What’s 6 times 6 divided by 2 plus 2
Answers
Answer: 20
Step-by-step explanation:
Find the value of a. Enter a numeric answer only.
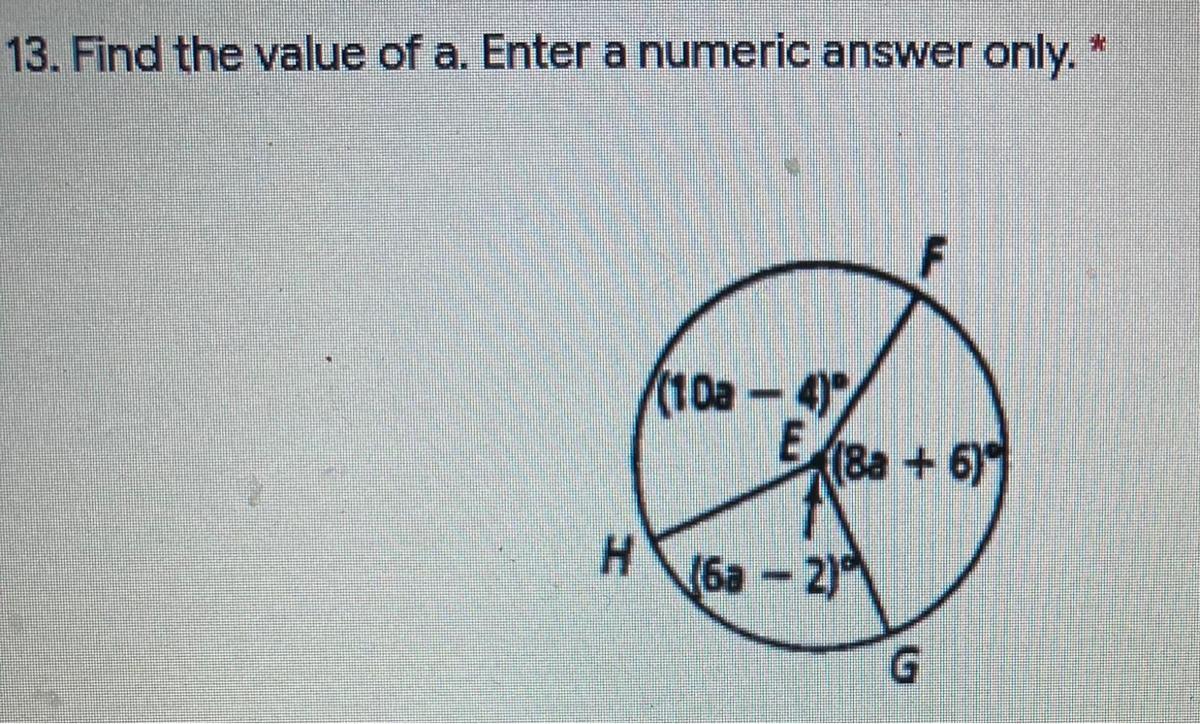
Answers
Solution
For this case we have the following, the sum of the angles needs to be 360 since we have a circumference:
10a-4 +6a-2 +8a+6=360
Regrouping we have:
10a +6a +8a -4 -2 +6= 360
24a= 360
a= 360/24= 15
Graph the following equation S = 25N

Answers
Answer:
On the graph
Step-by-step explanation:

Can someone please help me with this, it’s urgent!!

Answers
Answer:
Step-by-step explanation:
angle 4 is congruent to angle 4 because they are alternate interior angles.
angle 5 is congruent to angle 3 because they are alternate interior angles.
angle 1+angle 2+angle 3 is equal to (=) angle 1+angle 2+angle 3
angle 1+angle 2+angle 3=180 degree(being sum of interior angles of a trianngle)
A container of water holds 128 fluid ounces. Tyler drinks 4 fluid ounces of water every hour.
_________________ fluid ounces are in the container after 8 hours
(look at picture for more understanding)

Answers
Answer:96
Step-by-step explanation: 4x8 = 32 so there will be 32 fluid ounces gone. subtract that from 128 to get 96.
help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Step-by-step explanation:
-2x+4y=16
Subtract 4y from both sides
-2x+4y-4y=16-4y
Simplify
-2x=16-4y
Divide both sides by -2
-2x/-2=16/-2- 4y/-2
x=-2(-y+4)
Jamel plans to take a cruise that leaves out of New Orleans and needs to rent a car to see the sights as well as travel to and from the airport. The cost of renting a car is $50 plus $0.75 per mile for every mile over 40 miles driven. If Jamel's total cost for renting the car is $122.75, use the composition of functions to find how many miles Jamel drove the car on his vacation?

Answers
The number of miles that Jamel drove the car on his vacation was 97 miles.
Let the number of miles that he traveled be represented by x.
Based in the information given, the equation to solve the question will be:
50 + (0.75 × x) = 122.75
50 + 0.75x = 122.75
Collect like terms
0.75x = 122.75 - 50
0.75x = 72.75
Divide both side by 0.75
0.75x/0.75 = 72.75/0.75
x = 97
Therefore, Jamel drove the car for 97 miles.
Read related link on:
https://brainly.com/question/24685998
please answer this question

Answers
The value of m<2 = 107
Given:
m<SOX = 160
m<1 = x+14
m<2 = 3x - 10
x + 14 + 3x - 10 = 160
4x + 14 - 10 = 160
4x + 4 = 160
4x = 160 - 4
4x = 156
divide by 4 on both sides
4x/4 = 156/4
x = 39
m<2 = 3*39 - 10
= 117 - 10
= 107
Learn more about the value here:
https://brainly.com/question/14316282
#SPJ1
The weights of newborn babies are normally distributed with a mean of 8.5 pounds and a standard deviation of 2 pounds. A random sample of 25 newborns are selected.
b) Find the standard deviation of the mean of the 25 newborn babies. Round to 1 decimal place.
Answers
The standard deviation of the mean of the 25 newborn babies is approximately 0.4 pounds, rounded to 1 decimal place.
To find the standard deviation ,we will use the formula for the standard
deviation of the sampling distribution of the sample mean:
Standard deviation of the sample mean = σ / √n
Here, σ is the population standard deviation and
n is the sample size.
Given the population standard deviation (σ) is 2 pounds and the sample size (n) is 25 newborns, we can plug in the
values into the formula:
Standard deviation of the sample mean = 2 / √25
Standard deviation of the sample mean = 2 / 5
Standard deviation of the sample mean = 0.4
So, the standard deviation of the mean of the 25 newborn babies is approximately 0.4 pounds, rounded to 1 decimal place.
for such more question on standard deviation
https://brainly.com/question/1831755
#SPJ11
Write some examples of interval variables
Answers
An interval variable is a type of quantitative variable, where the difference between two values of the variable is meaningful and the values can be ordered.
Examples of interval variables include temperature (in Celsius or Fahrenheit), time (in seconds, minutes, hours, etc.), and dates. You can calculate the difference in temperature between two points, the length of time between two events, or the number of days between two dates. For example, let's say that the temperature outside is 25°C at noon and 29°C at 4 pm. The interval variable is the temperature, and the difference between the two temperatures is 4°C (29°C - 25°C = 4°C). Another example is the length of time between two events. Let's say that Event A began at 1 pm and Event B began at 2 pm. The interval variable is the length of time between the two events and the difference between the two times is 1 hour (2 pm - 1 pm = 1 hour). Finally, let's say that Date A is January 1, 2020 and Date B is January 10, 2020. The interval variable is the number of days between the two dates, and the difference between the two dates is 9 days (January 10,)An interval variable is a type of quantitative variable, where the difference between two values of the variable is meaningful and the values can be ordered.
Learn more about variable here:
https://brainly.com/question/2466865
#SPJ4
simplify fully
2/(5x)+2x/3
Answers
Answer:
16x / 15
Step-by-step explanation:
2/5x + 2x/3
6x - 10x /15
16x / 15
Find the area and the circumference of a circle with diameter 5 cm.
Use the value 3.14 for it, and do not round your answers. Be sure to include the correct units in your answers.
Answers
The Circumference of the circle is
15.7
and Area is
19.625
How many singlets are expected in the 1h nmr spectrum of 2,2,4,4-tetramethylpentane? 1 4 3 2
Answers
Only one singlet is expected in the 1H NMR spectrum of 2,2,4,4-tetramethylpentane. So, correct option is A.
In the 1H NMR spectrum, the number of singlets corresponds to the number of unique hydrogen environments in the molecule. Each unique hydrogen environment, where the hydrogens are chemically equivalent, will produce a singlet peak.
In 2,2,4,4-tetramethylpentane, all the carbons are identical, and each carbon is bonded to three hydrogen atoms. The four methyl groups (-CH3) are also chemically equivalent to each other. Therefore, all the hydrogens in this molecule are in equivalent environments, and there are no differences between them.
Since all the hydrogens are chemically equivalent, they will produce a single peak in the 1H NMR spectrum. This single peak is called a singlet.
Hence, the correct answer is option a, as only one singlet is expected in the 1H NMR spectrum of 2,2,4,4-tetramethylpentane.
To learn more about singlets click on,
https://brainly.com/question/31037641
#SPJ4
Answer: Two singlets.
Step-by-step explanation:
The methyl groups are all equivalent with no neighbors, so they all give rise to only 1 peak.
There is a methylene group that gives rise to another peak.
So the total is 2 singlets.
A bag contains 80 more red marbles than black marbles. Ifthe ratio of red marbles 9 to 4, how many marbles are in the bag in total?
Answers
The ratio of red marbles to black marbles is 9:4, this implies:
\(\frac{x+80}{x}=\frac{9}{4}\)By cross-multiplying and solving for x, we have:
\(\begin{gathered} 9x=4(x+80) \\ 9x=4x+320 \\ 9x-4x=320 \\ 5x=320 \\ x=\frac{320}{5} \\ x=64 \end{gathered}\)Thus, the number of red marbles is 64+80=144 and the number of black marbles is 64.
Hence, the total number of marbles in the bag is:
\(144+64=208\text{ marbles}\)If there are 3 servers in an infinite capacity Poison
queue system with λ = 12 hour and μ = 15 per hour, what is the
percentage of idle time for each server?
Answers
The percentage of idle time for each server can be represented as (1 - ρ) / 3.
In an infinite capacity Poison queue system with three servers, where the arrival rate (λ) is 12 customers per hour and the service rate (μ) is 15 customers per hour, we need to calculate the percentage of idle time for each server. The idle time refers to the time when a server is not serving any customer and there are no customers waiting in the queue. The percentage of idle time provides an indication of the efficiency and utilization of the servers in the system.
To calculate the percentage of idle time for each server, we can utilize the concept of the M/M/3 queuing system, where "M" represents the Markovian arrival process and "3" denotes the number of servers. In this system, the servers operate independently and can handle customer arrivals simultaneously.
In a stable queuing system, the traffic intensity (ρ) is defined as the ratio of the arrival rate (λ) to the total service rate (μ). In this case, the total service rate for three servers is 3μ. By calculating ρ = λ / (3μ), we can determine if the system is stable or not. If ρ < 1, the system is stable.
The percentage of idle time for each server can be obtained by subtracting the traffic intensity from 1 and then dividing it by the number of servers. This can be represented as (1 - ρ) / 3.
By plugging in the given values of λ and μ, we can calculate the traffic intensity (ρ) and then determine the percentage of idle time for each server using the derived formula. This will provide us with the information regarding the efficiency of each server and the amount of time they spend idle in the queuing system.
Learn more about queuing system here:
https://brainly.com/question/29585434
#SPJ11
A population of beetles is growing according to a linear growth model. The initial population is P0=3, and the population after 10 weeks is P10=103.
(a) Find an explicit formula for the beetle population after n weeks.
(b) How many weeks will the beetle population reach 183?
Answers
The beetle population, growing linearly, has an explicit formula P(n) = 3 + 10n, and it will take 18 weeks for the population to reach 183.
(a) To find an explicit formula for the beetle population after n weeks, we can use the information given in the problem. Since the growth model is linear, we can assume that the population increases by a constant amount each week.
Let's denote the population after n weeks as P(n). We know that P(0) = 3 (initial population) and P(10) = 103 (population after 10 weeks).
Since the population increases by a constant amount each week, we can find the growth rate (or increase per week) by taking the difference in population between week 10 and week 0, and dividing it by the number of weeks:
Growth rate = (P(10) - P(0)) / 10 = (103 - 3) / 10 = 100 / 10 = 10
Therefore, the explicit formula for the beetle population after n weeks can be written as:
P(n) = P(0) + (growth rate) * n
P(n) = 3 + 10n
(b) To find how many weeks it will take for the beetle population to reach 183, we can set up an equation using the explicit formula and solve for n:
P(n) = 183
3 + 10n = 183
Subtracting 3 from both sides:
10n = 180
Dividing both sides by 10:
n = 18
Therefore, it will take 18 weeks for the beetle population to reach 183.
To know more about explicit formula,
https://brainly.com/question/29113457
#SPJ11
3.) What is the measure of angle a in the triangle below?
a
50°

Answers
40°
Step-by-step explanation:
∠ACB = ∠DCE ( vertically opposite angle )
Now...
a + 90° + 50° = 180° ( the sum of interior angle of triangle is 180° )
a + 140° = 180°
a = 180° - 140°
a = 40°
hence the value of a is 40°
Opposite angles are congruent and equal in measure so the bottom angle is 50 and their is a right angle that is90. Sum of all three angles is 180.
50 + 90 + a = 180 so
It is 40.
let t : r5 →r3 be the linear transformation defined by the formula
Answers
The rank of the standard matrix for T is 2, which is determined by the number of linearly independent columns in the matrix.
To find the rank of the standard matrix for the linear transformation T: R^5 → R^3, we need to determine the number of linearly independent columns in the matrix.
The standard matrix for T can be obtained by applying the transformation T to the standard basis vectors of R^5.
The standard basis vectors for R^5 are:
e1 = (1, 0, 0, 0, 0),
e2 = (0, 1, 0, 0, 0),
e3 = (0, 0, 1, 0, 0),
e4 = (0, 0, 0, 1, 0),
e5 = (0, 0, 0, 0, 1).
Applying the transformation T to these vectors, we get:
T(e1) = (1 + 0, 0 + 0 + 0, 0 + 0) = (1, 0, 0),
T(e2) = (0 + 1, 1 + 0 + 0, 0 + 0) = (1, 1, 0),
T(e3) = (0 + 0, 0 + 1 + 0, 0 + 0) = (0, 1, 0),
T(e4) = (0 + 0, 0 + 0 + 1, 1 + 0) = (0, 1, 1),
T(e5) = (0 + 0, 0 + 0 + 0, 0 + 1) = (0, 0, 1).
The standard matrix for T is then:
[1 0 0 0 0]
[1 1 0 1 0]
[0 1 0 1 1]
To find the rank of this matrix, we can perform row reduction or use the concept of linearly independent columns. By observing the columns, we see that the second column is a linear combination of the first and fourth columns. Hence, the rank of the matrix is 2.
Therefore, the rank of the standard matrix for T is 2.
LEARN MORE ABOUT matrix here: brainly.com/question/28180105
#SPJ11
COMPLETE QUESTION - Let T: R5-+ R3 be the linear transformation defined by the formula T(x1, x2, x3, x4, x5) = (x1 + x2, x2 + x3 + x4, x4 + x5). (a) Find the rank of the standard matrix for T.
identify the tranfermatoin plz hury

Answers
Answer:
Rotation
Step-by-step explanation:
If that is an option
a newsletter publisher believes that 78% of their readers own a rolls royce. is there sufficient evidence at the 0.02 level to refute the publisher's claim? state the null and alternative hypotheses for the above scenario.
Answers
There is not enough information provided to determine if there is sufficient evidence at the 0.02 level to refute the publisher's claim. The null hypothesis is that proportion of readers owning a Rolls Royce is equal to 0.78 and alternative hypothesis is that proportion of readers owning a Rolls Royce is not equal to 0.78.
To determine if there is sufficient evidence at the 0.02 level to refute the newsletter publisher's claim that 78% of their readers own a Rolls Royce, we need to conduct a hypothesis test. Here are the null and alternative hypotheses for this scenario:
Null Hypothesis (H0): The proportion of readers who own a Rolls Royce is equal to 0.78 (P = 0.78)
Alternative Hypothesis (H1): The proportion of readers who own a Rolls Royce is not equal to 0.78 (P ≠ 0.78)
To test these hypotheses, follow these steps:
1. Collect a random sample of readers and record the number of Rolls Royce owners in the sample.
2. Calculate the sample proportion (p-hat) of Rolls Royce owners.
3. Calculate the test statistic using the formula: z = (p-hat - P) / sqrt(P * (1-P) / n), where P is the claimed proportion (0.78) and n is the sample size.
4. Determine the critical value for a two-tailed test at the 0.02 significance level (α = 0.02), which is approximately ±2.576 (from a z-table or calculator).
5. Compare the test statistic (z) to the critical value. If the test statistic is greater than or equal to the critical value or less than or equal to the negative critical value, reject the null hypothesis in favor of the alternative hypothesis. If not, fail to reject the null hypothesis.
Based on the results, you can determine if there is sufficient evidence to refute the publisher's claim at the 0.02 significance level. However, just based on the given information, there is not enough information to determine if there is sufficient evidence at the 0.02 level to refute the publisher's claim. We need the sample size.
Learn more about Null Hypothesis:
https://brainly.com/question/25263462
#SPJ11
Take the first 4 digits of your student number as the first number and the last 3 digits as the second number. Write the matlab code to find the greatest common divisor of these numbers using the Euclidean algorithm.
Answers
The required Matlab code to find the greatest common divisor of a number using the Euclidean algorithm is shown.
To find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm in MATLAB, you can use the following code:
% Replace '12345678' with your actual student number
studentNumber = '12345678';
% Extract the first 4 digits as the first number
firstNumber = str2double(studentNumber(1:4));
% Extract the last 3 digits as the second number
secondNumber = str2double(studentNumber(end-2:end));
% Find the GCD using the Euclidean algorithm
gcdValue = gcd(firstNumber, secondNumber);
% Display the result
disp(['The GCD of ' num2str(firstNumber) ' and ' num2str(secondNumber) ' is ' num2str(gcdValue) '.']);
Make sure to replace '12345678' with your actual student number. The code extracts the first 4 digits as the first number and the last 3 digits as the second number using string indexing. Then, the gcd function in MATLAB is used to calculate the GCD of the two numbers. Finally, the result is displayed using the disp function.
Learn more about Matlab code here:
https://brainly.com/question/30763780
#SPJ4
Please help! Brainliest! How are the functions y = 2x2 and y = 2x2 + 7 related? How are their graphs related?
A. Each output for y = 2x2 + 7 is 7 less than the corresponding output of y = 2x2. The graph of y = 2x2 + 7 is the graph of y = 2x2 translated down 7 units.
B. Each output for y = 2x2 + 7 is 7 greater than the corresponding output of y = 2x2. The graph of y = 2x2 + 7 is the graph of y = 2x2 translated up 7 units.
Answers
Option B is correct.
We have the two equations -
\(y= 2x^{2}\)
\(y=2x^{2} +7\)
We have determine how are these functions related and how are their graphs related.
What type of conic section is represented by equation -y = \($x^{2}\) ?A parabola is represented by the equation y = \($x^{2}\).
According to the question, we have -
\(y= f(x) = 2x^{2}\)
\(y=g(x)=2x^{2} +7\)
Refer to the image attached for graphs.
Now -
g(x) - f(x) = \(2x^{2} +7-2x^{2}\) = 7
Therefore - Each output for y = g(x) is greater than the corresponding output of y = f(x).
From the graph it is clear that the graph of y = g(x) is the graph of
y = f(x) translated up 7 units.
Hence, Option B is correct.
To solve more questions on functions and graphs, visit the link below -
https://brainly.com/question/2364381
#SPJ2

if a sample mean is 54.6, and this estimates the population mean with a margin of error of 3.9, then what is the 95% confidence interval ? (recall that the mean lies halfway between the lower and upper confidence interval limits.) from 50.7 to 58.5 from 50.7 to 54.6 from 52.64 to 56.56 from 46.8 to 62.4 from 46.96 to 62.24
Answers
The 95% confidence interval is from 50.7 to 58.5.
To calculate the 95% confidence interval, we'll need the sample mean, margin of error, and critical value. The critical value is determined by the confidence level and sample size. For a 95% confidence interval with a sample size of 30 or more, we can use the z-score of 1.96.
The formula for a confidence interval is: Confidence Interval = Sample Mean ± (Critical Value × Standard Error)where Standard Error = Standard Deviation / √n Given, Sample Mean = 54.6Margin of Error = 3.9Critical Value (z-score) = 1.96Using these values and plugging them into the formula, we get: Confidence Interval = 54.6 ± (1.96 × 3.9)Confidence Interval = 54.6 ± 7.644The lower limit of the interval is 54.6 - 7.644 = 46.956The upper limit of the interval is 54.6 + 7.644 = 62.244
To know more about confidence interval refer to-
brainly.com/question/24131141#
#SPJ11
Consider the following normal form game: L U 0,0 D 2-3 R 2, -2 1,-1 Assume that x > 0. Moreover, assume that Player Row chooses U with probability p and Player Column chooses L with probability q. a) Derive and plot players' best response functions (p on the horizontal axis and q on the vertical axis). b) Find all the Nash equilibria (pure and mixed strategies) of the above game. Illustrate your answer in a graph (p on the horizontal axis and q on the vertical axis. Comment. Consider now the following two-player simultaneous-move game, called the rock-paper-scissors-lizard game. R stands for rock, P for paper, S for scissors, and L for lizard. R beats S but loses against P and L; P beats R but loses against S and L; S beats P and L but loses against R; L beats R and P but loses against S. The payoff for winning is 1 and that for losing is -1; when both players choose the same strategy they each get 0. Assume that Player Row chooses R with probability r, P with probability p, and S with probability $ (similarly for Player Column). c) Write down the normal form representation of the game. d) Find all the Nash equilibria (pure and mixed strategies) of the game. Comment.
Answers
(a) Player Column's best response is given by:
BR_Column(p) = { L if p < 1/2, R if p > 1/2 (indifferent if p = 1/2)
(b) Where both players are indifferent between their available strategies.
(c) The normal form representation of the game is above.
(d) No player can gain an advantage by deviating from this strategy.
This equilibrium results in an expected payoff of 0 for each player.
(a) To derive the best response functions, we need to find the strategies that maximize the payoffs for each player given the mixed strategy of the other player.
Player Row's best response function:
If Player Column chooses L with probability q, Player Row's expected payoff for choosing U is 0q + 2(1-q) = 2 - 2q.
If Player Column chooses R with probability 1-q, Player Row's expected payoff for choosing U is 0*(1-q) + 1*q = q.
Therefore, Player Row's best response is given by:
BR_Row(q) = { U if q < 1/3, D if q > 1/3 (indifferent if q = 1/3)
Player Column's best response function:
If Player Row chooses U with probability p, Player Column's expected payoff for choosing L is 0p + 2(1-p) = 2 - 2p.
If Player Row chooses D with probability 1-p, Player Column's expected payoff for choosing L is 0*(1-p) + (-1)*p = -p.
Therefore, Player Column's best response is given by:
BR_Column(p) = { L if p < 1/2, R if p > 1/2 (indifferent if p = 1/2)
Plotting the best response functions on a graph with p on the horizontal axis and q on the vertical axis will result in two line segments: BR_Row(q) is horizontal at U for q < 1/3 and horizontal at D for q > 1/3, while BR_Column(p) is vertical at L for p < 1/2 and vertical at R for p > 1/2.
The two segments intersect at the point (p, q) = (1/2, 1/3).
(b) To find the Nash equilibria, we look for the points where the best response functions intersect. In this case, the only Nash equilibrium is at (p, q) = (1/2, 1/3), where both players are indifferent between their available strategies.
Now let's move on to the rock-paper-scissors-lizard game:
(c) The normal form representation of the game can be written as follows:
R P S L
------------------------
R | 0,0 -1,1 1,-1 1,-1
P | 1,-1 0,0 -1,1 1,-1
S | -1,1 1,-1 0,0 -1,1
L | -1,1 -1,1 1,-1 0,0
(d) To find the Nash equilibria, we look for any strategy profiles where no player can unilaterally deviate to improve their payoff.
In this game, there are no pure strategy Nash equilibria since each strategy can be countered by another strategy with a higher payoff.
However, there is a mixed strategy Nash equilibrium where each player chooses their actions with equal probabilities: r = p = s = l = 1/4.
In this case, no player can gain an advantage by deviating from this strategy.
This equilibrium results in an expected payoff of 0 for each player.
In summary, the rock-paper-scissors-lizard game has a unique mixed strategy Nash equilibrium where each player randomly chooses their actions with equal probabilities.
Learn more about Nash equilibrium from this link:
https://brainly.com/question/29398344
#SPJ11