Answers
Answer:
True
Step-by-step explanation:
Answer:
5
Step-by-step explanation:
15/3
Related Questions
The Chang family puts up holiday lights around their isosceles trapezoidal window. They use 20 feet of lights to go around the frame. How long is each leg of the window?
Answers
Answer:
\(P=a+b+c+d\)
Step-by-step explanation:
These are the steps to finding the trapezoid perimeter.
serenity held a fundraiser for her school and raised a total of $500. She received $150 in donations and then an additional $10 for every candle she sold.
Answers
Answer:
450 $ in tottle for every candle she sold.
Step-by-step explanation:
Complete the following, using ordinary interest. (Use Days in a year table.) (Do not round intermediate calculations. Round the "Interest" and "Maturity value" to the nearest cent.)
Principal: 1,000
Interest rate: 8%
Date borrowed: March 8
Date repaid: June 9
Exact time:
Interest:
Maturity value:
Answers
Answer:
75
Step-by-step explanation:
Which statements are true? Select three options. Line A B and Line C G are parallel. Line A B and Line R S are parallel. Line C G and Line R S are perpendicular. Line A B and Line R S must intersect. Line segment C G lies in plane X. Line segment R S lies in plane X.
Answers
Answer:
Line A B and Line C G are parallel.
Line C G and Line R S are perpendicular
Line A B and Line R S must intersect
Line segment C G lies in plane X
Step-by-step explanation:
Given that Planes X and Y intersect at a right angle.
From the image attached, line AB and CG are on the same plane X while line RS is on plane Y. Hence, line CG lies on plane X.
Since both line AB and CG line on the same plane, this means that both lines are parallel to each other.
Since plane X and plane Y are perpendicular to each other and line CG is on plane X and line RS is on plane Y, this means that both Line C G and Line R S are perpendicular.
Also Since plane X and plane Y intersect and line AB is on plane X and line RS is on plane Y, this means that both Line C G and Line R S intersect with each other at right angle.

Answer:
A and are parallel.
C and are perpendicular.
E lies in plane X.
Step-by-step explanation:
ED22
A bag contains 6 batteries, all of which are the same size and are equally likely to be selected. Each battery is a different brand. If you select 3 batteries at random, use the counting principle to determine how many points will be in the sample space if the batteries are selected
Answers
Answer:
there are 120 possible points in the sample space if we select 3 batteries at random from a bag containing 6 batteries of different brands.
Step-by-step explanation:
The counting principle states that if there are n ways to do one thing and m ways to do another, then there are n x m ways to do both.
In this case, we want to determine how many ways we can select 3 batteries out of 6. Using the counting principle, we can break down the selection process into three steps:
Select the first battery. There are 6 choices for the first battery.
Select the second battery. There are 5 choices left for the second battery, since we've already selected one.
Select the third battery. There are 4 choices left for the third battery.
Using the counting principle, we can multiply the number of choices for each step to get the total number of ways to select 3 batteries:
6 x 5 x 4 = 120
Therefore, there are 120 possible points in the sample space if we select 3 batteries at random from a bag containing 6 batteries of different brands.
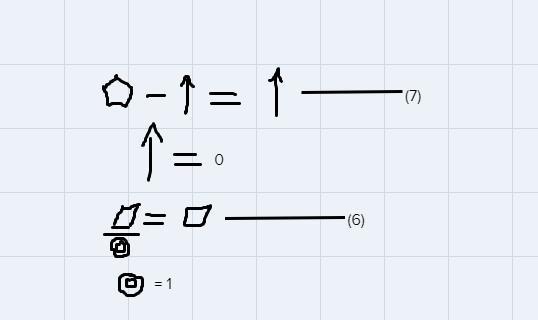
what does start equal if symbols below represent digits 0-9

Answers
The symbol shown in the table represents digits 0 to 9
We need to consider all the equations shown to e able to know the digit that each symbol represents
Since:
(Up arrow) ↑ = 0 (from equation 7)
Annular ring = 1 (from equation 6)
2 clockwisearrow = 10 (from equation 8)
clockwisearrow = 10/2
clockwisearrow = 5
From equation (4)
2 moon = triangle
Substitute equation (4) into equation (2)
moon x triangle = 2 moon
triangle = (2 moon) / moon
triangle = 2
equation 5: pentagon and arrowed circle are consecutive (because annular ring = 1). So pentagon can be only 3, 6, 7 or 8
equation 2: since pentagon is a multiple of two different integers, it can only be 6 or 8
Since triangle = 2, from equation (1), pentagon has to be 6, else, equation (1) will give a value greater than (8), the maximum value, and that is not possible.
Pentagon = 6
moon + moon = pentagon............(4)
2moon = pentagon
2moon = 6
moon = 6/2
moon = 3
The only missing nun



A gardener would like to add to their existing garden to make more flowers available for the butterflies that visit the garden. Her current garden is 20 square feet. If she added another rectangular piece with vertices located at (−18, 13), (−14, 13), (−18, 5), and (−14, 5), what is the total area of the garden?
640 ft2
320 ft2
52 ft2
32 ft2
tysm! :)
Answers
The total area of the garden is 52 ft².
How to find the total area of the garden
First we need to calculate the area of the current garden and the area of the rectangular piece that will be added, and then add them together.
The current garden has an area of 20 square feet.
To find the area of the rectangular piece that will be added, we can use the formula for the area of a rectangle:
Area = length x width
The length of the rectangle is the distance between the points (-18, 13) and (-14, 13), which is 4 units. The width of the rectangle is the distance between the points (-18, 13) and (-18, 5), which is 8 units.
Therefore, the area of the rectangular piece that will be added is:
Area = 4 x 8 = 32 square feet
The total area of the garden is the sum of the areas of the current garden and the rectangular piece that will be added:
Total area = 20 + 32 = 52 square feet
Therefore, the total area of the garden is 52 ft².
Learn more about square feet here :brainly.com/question/22889011
#SPJ1
The temperature in a hotel is 21 °C.
The temperature in the hotel is 26,7°C warmer than at the top of the mountain.
The temperature at the top of the mountain is 3.2°C colder than at the bottom of the mountain.
Work out the temperature at the bottom of the mountain.
Answers
The temperature at the bottom of the mountain is 50.9 °C.
Let's work through the given information step by step to find the temperature at the bottom of the mountain.
The temperature in the hotel is 21 °C.
The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.
Let's denote the temperature at the top of the mountain as T_top.
So, the temperature in the hotel can be expressed as T_top + 26.7 °C.
The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.
Let's denote the temperature at the bottom of the mountain as T_bottom.
So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.
Now, let's combine the information we have:
T_top + 26.7 °C = T_bottom - 3.2 °C
To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:
T_bottom = T_top + 26.7 °C + 3.2 °C
T_bottom = T_top + 29.9 °C
Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:
T_bottom = 21 °C + 29.9 °C
T_bottom = 50.9 °C
Therefore, the temperature at the bottom of the mountain is 50.9 °C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ8
Factor −5x2 + 10x.
PLS HURRY NEED THIS DUE TODAY
Answers
Answer:
C. 5x(-x + 2)
Step-by-step explanation:
To factor the expression -5x² + 10x, we need to look for a common factor that can be factored out.
Finding a common factor involves identifying a term or expression that can be factored out from each term of a given expression.
Both terms have the common factor of 5x, so we can factor out 5x:
5x(-x + 2)
Therefore, the factored form of -5x² + 10x is -5x(x - 2).
\(\hrulefill\)
Additional notes:
If we expand the expressions in the given answer options, we get:
A. −5x(x + 2) = -5x² - 10x
B. 5(−x² + 10x) = -5x² + 50x
C. 5x(−x + 2) = -5x² + 10x
D. x(5x + 10) = 5x² + 10x
Hence confirming that the correct answer is option C.
To factor \(-5x^2+10x\), we can begin by factoring out the greatest common factor, which is \(-5x\):
\(-5x^2 + 10x = \boxed{-5x(x - 2)}\)We can check our answer by distributing \(-5x\) to the expression inside the parentheses:
\(\begin{aligned}-5x(x - 2)& = (-5x)(x) + (-5x)(-2)\\& = -5x^2 + 10x\end{aligned}\)\(\therefore\) The answer is \(-5x(x-2)\).
\(\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}\)
Help ASAP Please. Working on this now. Look at picture for question and answer A, B, C. No Plagiarism Please. Will Mark Brainliest.

Answers
Answer:
Please check explanations for answer to the question
Step-by-step explanation:
The exponential relation can generally be represented as ;
y = I (1 + x)^n
where I is the initial value
1 + x represents the growth rate
n represents the time such as number of years
y represents the value after n count
a) The value 1200 represents the initial count of bacteria in the study
b) 1.8 represents the growth rate of the bacteria population in the culture
c) 1000 represents the initial bacteria population in the second function
The difference mean that the initial population in the first case study is greater than what we have in the second function
Find the derivative of y=3x/(x^2 + 1)
Answers
To find the derivative of
\(y=\frac{3x}{x^2+1},\)we will use the division rule for derivatives.
The division rule states that:
\((\frac{f(x)}{g(x)})^{\prime}=\frac{f^{\prime}(x)g(x)-g^{\prime}(x)f(x)}{g(x)^2}.\)Therefore, the derivative of the given quotient is:
\(y^{\prime}=\frac{(3x)^{\prime}(x^2+1)-(x^2+1)^{\prime}(3x)}{(x^2+1)^2}.\)Simplifying the above result we get:
\(\begin{gathered} y^{\prime}=\frac{3(x^2+1)-(2x\cdot3x)}{(x^2+1)^2}=\frac{3(x^2+1)-6x^2}{(x^2+1)^2}=\frac{3(x^2+1-2x^2)}{(x^2+1)^2} \\ =\frac{3(1-x^2)}{(x^2+1)^2}. \end{gathered}\)Answer:
\(y^{\prime}=\frac{3(1-x^2)}{(x^2+1)^2}.\)Find the slope of the line passing through the points (-2,3) a
and
(-9,6).
Answers
===================================================
Apply the slope formula
m = (y2-y1)/(x2-x1)
m = (6-3)/(-9-(-2))
m = (6-3)/(-9+2)
m = 3/(-7)
m = -3/7
This means each time you go down 3 units, you go to the right 7 units.
Slope = rise/run = -3/7
rise = -3 and run = 7
what is the value of x
Answers
Answer:
x could be anything
Step-by-step explanation:
Hurry - Fill in the blanks


Answers
Answer:
The first value of a relation is an input value and the second value is the output value. A function is a specific type of relation in which each input value has one and only one output value.
An input is an independent value, and the output value is the dependent value, as it depends on the value of the input.
I need help with this problem.

Answers
Answer:
correct answer is marked
Step-by-step explanation:
You can work with the letters in the similarity statement, or you can work with the diagram.
The corresponding sides are ...
AC and BC
AE and BD
CE and CD
If you choose a pair on the left of this list, the proportion is written using the corresponding pair on the right of this list. Using the first two lines, we can write ...
AC/AE = BC/BD . . . . matches the first choice
What else would need to be congruent to show that ABC DEF by SAS? E AA. А B OA. BC = EF B. CF OC. ZA ZD D. AC = OF F Given: AC = DF CE F

Answers
The two triangles exist congruent if they contain two congruent corresponding sides and their contained angles exist congruent.
Let \($&\overline{A B} \cong \overline{D E} \\\) and \($&\overline{A C} \cong \overline{D F}\)
Angle between \($\overline{A B}$\) and \($\overline{A C}$\) exists \($\angle A$\).
Angle between \($\overline{D E}$\) and \($\overline{D F}$\) exists \($\angle D$\).
Therefore, \($\triangle A B C \cong \triangle D E F$\) by SAS, if \($\angle A \cong \angle D$$\).
What is SAS congruence property?Given:
\($&\overline{A B} \cong \overline{D E} \\\) and
\($&\overline{A C} \cong \overline{D F}\)
According to the SAS congruence property, two triangles exist congruent if they contain two congruent corresponding sides and their contained angles exist congruent.
Let \($&\overline{A B} \cong \overline{D E} \\\) and \($&\overline{A C} \cong \overline{D F}\)
Angle between \($\overline{A B}$\) and \($\overline{A C}$\) exists \($\angle A$\).
Angle between \($\overline{D E}$\) and \($\overline{D F}$\) exists \($\angle D$\).
Therefore, \($\triangle A B C \cong \triangle D E F$\) by SAS, if \($\angle A \cong \angle D$$\).
To learn more about SAS congruence property refer to:
https://brainly.com/question/19807547
#SPJ9
yesterday, the temperature at noon was 12 Fahrenheit. by midnight, the temperature had decreased by 16 degrees Fahrenheit. which expression represents the temperature at midnight?
A. 12+16
B. 12+ 16
C. -12 + 16
D. -12 + -16
Answers
Answer:
C
Step-by-step explanation:
The heights of adult men in America are normally distributed, with a mean of 69.8 inches and a standard deviation of 2.69 inches. The heights of adult women in America are also normally distributed, but with a mean of 64.1 inches and a standard deviation of 2.55 inches.
Required:
a. If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)?
b. What percentage of men are SHORTER than 6 feet 3 inches?
c. If a woman is 5 feet 11 inches tall, what is her z-score (to two decimal places)?
d. What percentage of women are TALLER than 5 feet 11 inches?
Answers
Answer:
a) 1.93
b) 97.32% of men are SHORTER than 6 feet 3 inches
c) 2.71
d) 0.34% of women are TALLER than 5 feet 11 inches
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
a. If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)?
For man, \(\mu = 69.8, \sigma = 2.69\)
A feet has 12 inches, so this is Z when X = 6*12 + 3 = 75. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{75 - 69.8}{2.69}\)
\(Z = 1.93\)
b. What percentage of men are SHORTER than 6 feet 3 inches?
Z = 1.93 has a pvalue of 0.9732
97.32% of men are SHORTER than 6 feet 3 inches
c. If a woman is 5 feet 11 inches tall, what is her z-score (to two decimal places)?
For woman, \(\mu = 64.1, \sigma = 2.55\)
Here we have X = 5*12 + 11 = 71.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{71 - 64.1}{2.55}\)
\(Z = 2.71\)
d. What percentage of women are TALLER than 5 feet 11 inches?
Z = 2.71 has a pvalue of 0.9966
1 - 0.9966 = 0.0034
0.34% of women are TALLER than 5 feet 11 inches
help plz can you explain some one plz

Answers
Answer:
Sheila drove 30 more miles than Adam
Step-by-step explanation:
After three hours Sheila drove 150 miles, and after three hours Adam drove 120 miles
In triangle OPQ, p = 38 cm, q = 29 cm and Angle O=39º. Find the length of o, to the nearest
centimeter.
Answers
Answer:
The length of o is 24 centimeters
Step-by-step explanation:
In Δ OPQ
∵ Side p is opposite to ∠P
∵ Side q is opposite to ∠Q
∵ Side o is opposite to ∠O
→ To find side o we must use the cosine rule
∴ o = \(\sqrt{p^{2}+q^{2}-2(p)(q).cos(O) }\)
∵ p = 38 cm
∵ q = 29 cm
∵ m∠O = 39°
→ Substitute them in the rule to find o
∴ o = \(\sqrt{(38)^{2}+(29)^{2}-2(38)(29).cos(39)}\)
∴ o = 23.92008154
→ Round it to the nearest centimeter (whole number)
∴ o = 24 centimeters
∴ The length of o is 24 centimeters
Please help! (Attached image) remainder Theorem

Answers
Answer:
First is option B)
Second is option B)
I hope my answer helps you.
A graph shows the survey results for a group of students who
were asked how many honors classes they have taken and
how many elective classes:
Class Choices
Number of Elective Classes
0
lo 1 2 3
4
5 6 7 8
9 10 11
Number of Honors Classes
How many elective classes would students likely have taken if
they have taken 12 honors classes? (4 points)
Answers
write answers that are not integers rounded to the nearest tenth

Answers
The value of x is 12.82, the value of z is 40.25.
Using Pythagorean theorem
50²= 39² + y²
y²= 2500- 1521
y= 32.28
Again Using Pythagorean theorem
z²= y²+ x²
z²- x²= 979
and, (39 + x)² = 50² + z²
(39 + x)² = 50² + (x² + 979)
1521 + 78x + x² = 2500 + x² + 979
78x = 1000
x ≈ 12.82
Substituting this value of x back into the first equation, we get:
z² - x² = 979
z² - (12.82)² = 979
z² ≈ 1620.12
Taking the square root of both sides, we get:
z ≈ 40.25
Therefore, the value of x is 12.82, the value of z is 40.25.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
how to work out the mode
Answers
Hope this helps, have an awesome day. <3
Which expression has a value of 15 when p = 12?

Answers
Answer:p+3
Step-by-step explanation:
I just took the test trust me homie.
How do you put 2hundreds 9tens 18ones in standard form
Answers
Answer:
308
Step-by-step explanation:
200+90+18=200+108=308
three hundred seven
or
307
Step-by-step explanation:
I can't remember which is standard form. But hope it helps.
write an equation for a line parallel to y = − 2 x − 3 and passing through the point (3,-3)
Answers
Equation of line parallel to y = − 2 x − 3 and passing through the point (3,-3) is y = -2x + 3.
When two lines are called parallel?
Two lines are parallel lines if they do not intersect.
The slopes of the lines are the same.
f(x)= mx + b and g(x)= nx + c are parallel if m = n.
According to the given question:
Given equation of line is y = −2x − 3
If the new line is parallel, then it will have the same slope.
y = -2x + b
Now this line passes through the point (x,y) = (3,-3) so put in the x and y values into the equation above, solve for b
-3 = -2(3) + b
b = 3
Therefore the required equation of line is
y = -2x + 3
To know more about parallel lines visit
https://brainly.com/question/13228195
#SPJ1
Really need help fast!! Will give BRAINLIEST

Answers
Answer: the answer is C.
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
AM = MB is dependant, that means that M has to be the midpoint first before those two
(-52 + x – 5) – (–70² – 7x – 3)
Answers
Answer:
7x+4846
Step-by-step explanation:
-5 1/4 -(-7 1/2) simplify
really fast pleas
