The length of the escalator is 36 ft and the
vertical height it rises is 9 ft. what is the angle
of elevation?
a. 90
b. 75. 52
c. 14. 48
d. 14. 04
Answers
Answer:
sin θ = 9 / 36 = 1/4
θ = 14.48 deg (ans C)
Related Questions
Choose the polynomial that is written in standard form. X 4x5 10x3 x4 4x2 8x −9x4 4x6 10x2 x4 4x4 x6.
Answers
Answer:
B. X4+ 4x2 +8x is the answer
Step-by-step explanation:
Answer:
B x4 + 4x2 + 8x
Step-by-step explanation:
How patriotic are you? Would you say extremely patriotic, very patriotic, somewhat patriotic, or not especially patriotic? Below is the data from Gallup polls that asked this question of a random sample of U.S. adults in 1999 and a second independent random sample in 2010. We conducted a chi-square test of homogeneity to determine if there are statistically significant differences in the distribution of responses for these two years. In this results table, the observed count appears above the expected count in each cell. 1999 994 extremely patriotic very patriotic somewhat patriotic not especially patriotic Total 193 466 284 257.2 443.8 237.3 55.72 324 426 193 611004 259.8 448.2 239.7 517 892 477 112 1998 2010 56.28 Total Chi-Square test: Statistic DF Value P-value Chi-square 3 53.19187) <0.0001 If we included an exploratory data analysis with the test of homogeneity, the percentages most appropriate as part of this analysis for the Extremely Patriotic group are
a. 193/1517 compared to 994/1998 b. 193/1998 compared to 324/1998 c. 193/517 compared to 324/517 d. 193/994 compared to 324/1004
Answers
The appropriate percentages for the Extremely Patriotic group are 19.42% in 1999 and 32.27% in 2010, corresponding to option d: 193/994 compared to 324/1004.
To calculate the appropriate percentages for the Extremely Patriotic group, we need to compare the counts from the 1999 and 2010 samples.
In 1999:
Number of Extremely Patriotic responses: 193
Total number of respondents: 994
In 2010:
Number of Extremely Patriotic responses: 324
Total number of respondents: 1004
Now we can calculate the percentages:
Percentage for 1999: (193 / 994) × 100 = 19.42%
Percentage for 2010: (324 / 1004) × 100 = 32.27%
Therefore, the appropriate percentages as part of the exploratory data analysis for the Extremely Patriotic group are:
19.42% compared to 32.27% (option d: 193/994 compared to 324/1004).
To know more about appropriate percentages:
https://brainly.com/question/28984529
#SPJ4
Hello can you help me solve this question please

Answers
Answer: Radius=19.2 diameter=38.39
Step-by-step explanation: :DDD
A man bought 300pen at Rs6 each of them sold them at Rs 90 per dozen. find his profit

Answers
I hope this help you


Prove that if n^2 + 8n + 20 is odd, then n is odd for natural numbers n.
Answers
Answer:
If n is even, then n^2 + 8n + 20 is even.
Let n = 2k (k = 0, 1, 2,...). Then:
(2k)^2 + 8(2k) + 20 = 4k^2 + 16k + 20
= 4(k^2 + 4k + 5)
This expression is even for all k, so if n is even, this expression is even.
So if n^2 + 8n + 20 is odd, then n is odd.
Natural numbers n must be odd for n^2 + 8n + 20 to be odd.
To prove that if n^2 + 8n + 20 is odd, then n is odd for natural numbers n, we can use proof by contradiction.
Assume that n is even for some natural number n. Then we can write n as 2k for some natural number k.
Substituting 2k for n, we get:
n^2 + 8n + 20 = (2k)^2 + 8(2k) + 20
= 4k^2 + 16k + 20
= 4(k^2 + 4k + 5)
Since k^2 + 4k + 5 is an integer, we can write the expression as 4 times an integer. Therefore, n^2 + 8n + 20 is divisible by 4 and hence it is even.
But we are given that n^2 + 8n + 20 is odd. This contradicts our assumption that n is even.
Therefore, our assumption is false and we can conclude that n must be odd for n^2 + 8n + 20 to be odd.
In detail, we have shown that if n is even, then n^2 + 8n + 20 is even. This is a contradiction to the premise that n^2 + 8n + 20 is odd. Therefore, n must be odd for n^2 + 8n + 20 to be odd.
Learn more about Natural numbers
brainly.com/question/17429689
#SPJ11
there are about 795 house in this region . the average family size is 6 people . there
are about __________ people living in the region
then round off your answer to the nearest tens .
Answers
Answer:
4770 people
Step-by-step explanation:
795*6= 4770
Customers of an internet service provider connect to the internet at the average rate of 12 new connections per minute. Connections are modeled by a Binomial counting process.
(a) What frame length Δ gives the probability 0.15 of an arrival during any given frame?
(b) With this value of Δ, compute the expectation and standard deviation for the number of seconds between two consecutive connections.
Answers
With a frame length of 1, the expectation is 5 seconds and the standard deviation is approximately 3.464 seconds for the number of seconds between two consecutive connections.
(a) To determine the frame length Δ that gives a probability of 0.15 of an arrival during any given frame, we need to consider the Binomial counting process and its probability distribution.
In a Binomial distribution, the probability of success (an arrival) is given by p, and the probability of failure (no arrival) is given by q = 1 - p. In this case, p = 12 connections per minute.
We can use the cumulative distribution function (CDF) of the Binomial distribution to find the frame length Δ. The CDF gives the probability of having k or fewer arrivals in a given number of frames.
Using a binomial probability table or a calculator, we find that when p = 0.15, the corresponding value of k is 1. Therefore, the frame length Δ that gives a probability of 0.15 of an arrival during any given frame is 1 frame.
(b) With a frame length Δ of 1, we can compute the expectation (mean) and standard deviation for the number of seconds between two consecutive connections.
The average rate of connections is 12 per minute. To find the average time between two consecutive connections, we take the reciprocal of the rate: 1/12 minutes per connection.
To convert minutes to seconds, we multiply by 60: (1/12) * 60 = 5 seconds.
Therefore, the expectation (mean) for the number of seconds between two consecutive connections is 5 seconds.
The standard deviation can be calculated using the formula for the standard deviation of a Poisson process, which is the limit of the Binomial distribution as the number of trials becomes large. For a Poisson process, the standard deviation is equal to the square root of the average rate: √(12) ≈ 3.464 seconds.
For more such questions on Standard deviation:
https://brainly.com/question/12402189
#SPJ8
three of the angles of a quadrilateral are 100, 104 and 44. what is the size of the 4th angle?
Answers
Answer:
112
Step-by-step explanation:
Sum of interior angles in quadrilaterial = 360
360 - 100 - 104 - 44 = 112
Step-by-step explanation:
Let the 4th angle = x
Now,
x + 100 + 104 + 44 = 360° ( the sum of interior angle of quadrilateral is 360°)
x + 248 = 360°
x = 360° - 248
x = 112
Hence, the fourth angle is 112....
The profit (p) a baker earned, in dollars, is proportional to the number of muffins (m) sold. This equation represents this relationship.
P = 0.75m
enter the profit earned for each muffin sold.
Answers
P = 0.75m represents the proportional relationship, therefore, the profit earned for each muffin sold is: $0.75.
What is Proportional Relationship?If two variables, i.e. P and m are directly proportional to each other, the relationship between them can be represented as P = km, where k is the constant.
Given that P = 0.75m represents the proportional relationship between the profit earned and muffins sold, the constant, k, is 0.75, which is the profit earned for each muffin sold.
Learn more about proportional relationship on:
https://brainly.com/question/15618632
solve the equation "-12x + 4"
Answers
Answer: -4(3x-1)
Step-by-step explanation:
A volleyball player sets a volleyball straight up into the air. The height of the volleyball, , is modeled by this equation, where t represents the time, in seconds, after that ball was set.
The volleyball reaches its maximum height after 0.625 seconds. What is the maximum height of the volleyball?
Answers
Answer:
The maximum height of the volleyball is 12.25 feet.
Step-by-step explanation:
The height of the volleyball, h(t), is modeled by this equation, where t represents the time, in seconds, after that ball was set :
....(1)
The volleyball reaches its maximum height after 0.625 seconds.
For maximum height,
Put
Now put t = 0.625 in equation (1)
Hope this helps!!
help asap for brainlist

Answers
Answer:
Option D
Step-by-step explanation:
(x + 8) (2x² - 5x - 3)
=> (2x³ - 5x² - 3x) + (16x² - 40x - 24)
=> 2x³ + 11x² - 43x - 24
Hope this helps!
Select the slope (m) and y-intercept. 3y=2x-3
Answers
Answer:
Divide each term by
3
and simplify.
Tap for more steps...
y
=
2
x
3
+
1
Use the slope-intercept form to find the slope and y-intercept.
Tap for more steps...
Slope:
2
3
y-intercept:
1
Any line can be graphed using two points. Select two
x
values, and plug them into the equation to find the corresponding
y
values.
Tap for more steps...
x
y
0
1
3
3
Graph the line using the slope and the y-intercept, or the points.
Slope:
2
3
y-intercept:
1
x
y
0
1
3
3
Step-by-step explanation:

A significance test about a proportion is conducted using a significance level of 0.05. The sample statistic is 0.12. The p-value is 0.03? a) If H0 were true, for what probability of a Type I error was the test designed?
b) What conclusion (reject or fail to reject) would you make for this test?
c) If this test resulted in a decision error, what type of error was it?
Answers
Answer: 28282
Step-by-step explanation:
I think
HELPPPPPPPPPP!!!!!!!
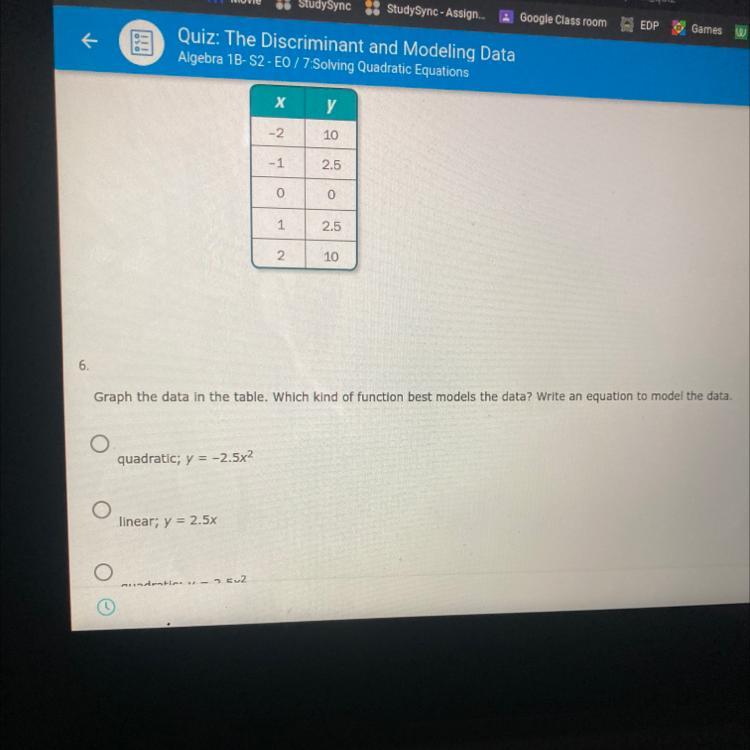
Answers

Yo plz help I have no clue what im doing

Answers
Answer:
hi
Step-by-step explanation:
if four dice are rolled, what is the probability that each of the four numbers that appear will be different?
Answers
Answer:
When four dice are rolled, there are 6 x 6 x 6 x 6 = 1296 possible outcomes, since each die has 6 possible outcomes and the rolls are independent.
To find the probability that each of the four numbers that appear will be different, we need to count the number of outcomes where each die shows a different number. We can do this by breaking it down into cases:
Case 1: The first die shows any number. The second die must show a different number than the first, so there are 5 possible outcomes. The third die must show a different number than the first two, so there are 4 possible outcomes. The fourth die must show a different number than the first three, so there are 3 possible outcomes. Therefore, there are 5 x 4 x 3 = 60 outcomes in this case.
Case 2: The first die shows any number. The second die shows the same number as the first. There is only 1 possible outcome in this case. The third die must show a different number than the first two, so there are 5 possible outcomes. The fourth die must show a different number than the first three, so there are 4 possible outcomes. Therefore, there are 1 x 5 x 4 = 20 outcomes in this case.
Case 3: The first die shows any number. The second die shows a different number than the first. The third die shows the same number as either the first or the second. There are 2 possible outcomes in this case. The fourth die must show a different number than the first three, so there are 4 possible outcomes. Therefore, there are 2 x 4 = 8 outcomes in this case.
To get the total number of outcomes where each die shows a different number, we add up the outcomes from each case:
60 + 20 + 8 = 88
Therefore, the probability that each of the four numbers that appear will be different is:
88 / 1296 = 0.0679, or approximately 6.79%.
draw the directed graph that represents the relation {(a, a), (a, b), (b, c), (c, b), (c, d), (d, a), (d, b)}.
Answers
The directed graph for the given values given by the relation {(a, a), (a, b), (b, c), (c, b), (c, d), (d, a), (d, b)} is expained.
The directed graph that represents the relation {(a, a), (a, b), (b, c), (c, b), (c, d), (d, a), (d, b)} is shown below:
We can clearly see from the directed graph that there are four vertices: a, b, c, and d.
For the given relation, there are three edges that start and end on vertex a, two edges that start and end on vertex b, one edge that starts from vertex c and ends on vertex b, one edge that starts from vertex c and ends on vertex d, and one edge that starts from vertex d and ends on vertex a.
The vertex a is connected to vertex a and b.
The vertex b is connected to vertices c and d.
The vertex c is connected to vertices b and d.
The vertex d is connected to vertices a and b.
A directed graph is a graphical representation of a binary relation in which vertices are connected by arrows.
Each directed edge shows the direction of the relation.
A directed graph is also called a digraph.
Know more about the binary relation
https://brainly.com/question/28682743
#SPJ11
Please help! Correct answer only please!
The formula for a baseball player's slugging percentage is:
1S + 2D + 3T+ 4HR/AB
If a player has 58 singles, 24 doubles, 8 triples, and 39 home runs, with 367 At Bats.
What is the player's slugging percentage?

Answers
What is the solution to the
system of equations graphed below?
y = x- 2
y = 3x - 2
Answers
Answer:
(0, -2)
Step-by-step explanation:
The solution to a system of equations is the point on the graph where the lines intersect.
SolutionHere, both lines have a y-intercept of -2, so intersect there. The solution is ...
(x, y) = (0, -2)

Which expression represents the length of QR?
Answers
Answer:
jsjdkfnfnfkdkfkfkfkidkffbgngngkgk
you have a solution that is 1 gr/tbsp. how many grams are in 2 pt?
Answers
To convert grams per tablespoon to grams per pint, we need to know the conversion factor between tablespoons and pints.
Since there are 2 tablespoons in 1 fluid ounce (oz), and there are 16 fluid ounces in 1 pint, we can calculate the conversion factor as follows:
Conversion factor = (2 tablespoons/1 fluid ounce) (1 fluid ounce/16 fluid ounces) = 1/8
Given that the solution is 1 gram per tablespoon, we can multiply this value by the conversion factor to find the grams per pint:
Grams per pint = (1 gram/tablespoon) (1/8) 2 pints = 0.25 grams
Therefore, there are 0.25 grams in 2 pints of the solution.
Learn more about Gram here :
https://brainly.com/question/29127168
#SPJ11
in a sample of 200 observations, there were 60 positive outcomes. find the standard error for the sample proportion.
Answers
The standard error for the sample proportion is 0.3995.
Standard Error: What Is It?
The standard error of the mean, or simply standard error, indicates how likely it is that the population means will differ from a sample mean. It demonstrates how much the sample means would vary if the same study were conducted again using new samples taken from the same population.
given:
n= 200
and possible outcomes= 80
Standard deviation = √(80²/200)= 5.65
Now, standard error = σ / √n
= 5.65/√200
= 0.3995
Hence, the standard error for the sample proportion is 0.3995.
Learn more about standard error here:
brainly.com/question/13179711
#SPJ4
Two lines meet at a point that is also the vertex of an angle. Set up and solve an equation to find the value of x
Answers
The value of x is the vertex of an angle with angles measuring 120 degrees and 240 degrees.
To solve this problem, we need to use the fact that the sum of the angles around a point is 360 degrees. This means that the angles formed by the two lines at the point of intersection add up to 360 degrees.
Let's call the two angles A and B. Then we can set up the following equation:
A + B = 360
Now, we need to use some information about the angle with vertex x to solve for one of the angles. Depending on the information given in the problem, we may need to use additional equations.
If we are given that one of the angles is twice the size of the other angle, we can write:
A = 2B
Now we can substitute this into our equation:
2B + B = 360
Simplifying, we get:
3B = 360
Dividing both sides by 3, we get:
B = 120
Now that we know the value of one of the angles, we can use our equation to find the value of the other angle:
A + 120 = 360
Subtracting 120 from both sides, we get:
A = 240
To know more about equation here
https://brainly.com/question/10413253
#SPJ1
Complete Question:
Two lines meet at a point that is also the vertex of an angle. Set up and solve an equation to find the value of x. Explain why your answer is reasonable.
A construction crew needs to pave a road that is 209 miles long. The crew paves 8 miles of the road each day. The length, L (in miles), that is left to be paved after d days is given by the following function.
L(d)=209-8d
Question a.)
If 154 miles of the road is left to be paved, how many days has the crew been paving the road?
Question b.)
How many miles of the road does the crew have left to pave after 13 days?
Answers
Answer:
a) 6 7/8 days
b) 105 miles
Step-by-step explanation:
Given that L(d) = 209 -8d miles of road remain to be paved after d days, you want to know (a) the number of days paving if 154 miles remain, and (b) remaining miles after 13 days.
a) Paving daysWe want to find d such that L(d) = 154.
L(d) = 154
209 -8d = 154 . . . . . . substitute for L(d)
209 -154 = 8d . . . . . add 8d-154
55/8 = d = 6 7/8 . . . divide by 8
The crew has been paving for 6 7/8 days if 154 miles remain.
b) Remaining milesAfter 13 days, the remaining miles will be ...
L(13) = 209 -8·13 = 209 -104
L(13) = 105
After 13 days, the crew has 105 miles left to pave.
<95141404393>

Suppose you plan to spend no more than $24 on meat for a cookout. Hamburger costs $3.00/lb and chicken wings cost $2.40/lb. Write and graph an equation to find three possible combinations of hamburger and chicken wings you can buy
Answers
Answer:
1. 8 hamburgers2. 10 chicken wings3. 4 hamburgers and 5 chicken wingsStep-by-step explanation:
Hamburger costs $3.00/lb Chicken wings cost $2.40/lbTotal = $24Required equation is:
3x + 2.4y = 24The graph is attached
Possible combinations are:
8 hamburgers10 chicken wings4 hamburgers and 5 chicken wings
angle sum theory
A) 10
B) 17
C) 3
D) 12

Answers
Answer:
C
Step-by-step explanation:
AWNSER: 3 :)
The Hoylake Rescue Squad receives an emergency call every 1, 2, 3, 4, 5, or 6 hours, according to the following probability distribution. The squad is on duty 24 hours per day, 7 days per week: a. Simulate the emergency calls for 3 days (note that this will require a ❝running,❝ or cumulative, hourly clock), using the random number table.
b. Compute the average time between calls and compare this value with the expected value of the time between calls from the probability distribution. Why are the results different?
Answers
The results are different because the simulated data is based on random numbers and may not perfectly match the probability distribution.
To simulate the emergency calls for 3 days, we need to use a cumulative hourly clock and generate random numbers to determine when the calls will occur. Let's use the following table of random numbers:
Random Number Call Time
57 1 hour
23 2 hours
89 3 hours
12 4 hours
45 5 hours
76 6 hours
Starting at 12:00 AM on the first day, we can generate the following sequence of emergency calls:
Day 1:
12:00 AM - Call
1:00 AM - No Call
3:00 AM - Call
5:00 AM - No Call
5:00 PM - Call
Day 2:
1:00 AM - No Call
2:00 AM - Call
4:00 AM - No Call
7:00 AM - Call
8:00 AM - No Call
11:00 PM - Call
Day 3:
12:00 AM - No Call
1:00 AM - Call
2:00 AM - No Call
4:00 AM - No Call
7:00 AM - Call
9:00 AM - Call
10:00 PM - Call
The average time between calls can be calculated by adding up the times between each call and dividing by the total number of calls. Using the simulated data from part a, we get:
Average time between calls = ((2+10+10+12)+(1+2+3)) / 7 = 5.57 hours
The expected value of the time between calls can be calculated using the probability distribution:
Expected value = (1/6)x1 + (1/6)x2 + (1/6)x3 + (1/6)x4 + (1/6)x5 + (1/6)x6 = 3.5 hours
The results are different because the simulated data is based on random numbers and may not perfectly match the probability distribution. As more data is generated and averaged, the simulated results should approach the expected value.
To learn more about Probability :
https://brainly.com/question/24756209
#SPJ11
You decide to travel by car for your holiday visits this year. You leave early in the morning to avoid congestion on the roads. This enables you to drive at a comfortable speed of v1=65.6mph for t1=2.08 hours. However, after this time, you unexpectedly come to a stop for tsop =33.6 min. Traffic starts moving again and you finish your travel at v2=57.2mph for an additional t2=1.25 hours. There are 1609 meters in one mile. What was the total distance d traveled? d= Incorrect What was the average speed vˉ?
Answers
The total distance traveled is approximately 207.948 miles and the average speed is approximately 53.48 mph.
To find the total distance traveled, we need to calculate the distance traveled during each segment of the journey and then sum them up.
Distance traveled during the first segment:
```
d1 = v1 * t1
= 65.6 mph * 2.08 hours
```
Distance traveled during the stop:
Since the car comes to a stop, the distance traveled during this time is zero.
Distance traveled during the second segment:
```
d2 = v2 * t2
= 57.2 mph * 1.25 hours
```
Now we can calculate the total distance traveled:
```
d = d1 + d2
```
Let's calculate the values:
```
d1 = 65.6 mph * 2.08 hours = 136.448 miles
d2 = 57.2 mph * 1.25 hours = 71.5 miles
d = d1 + d2 = 136.448 miles + 71.5 miles = 207.948 miles
tstop = 33.6 min = 33.6/60 hours = 0.56 hours
= 207.948 miles / (2.08 hours + 0.56 hours + 1.25 hours) = 207.948 miles / 3.89 hours ≈ 53.48 mph
```
Therefore, the total distance traveled is approximately 207.948 miles and the average speed is approximately 53.48 mph.
Learn more about distance here
https://brainly.com/question/30395212
#SPJ11
Solve the following first-order DEs: (e2y−ycos(xy))dx+(2xe2y−xcos(xy)+2y)dy=0 (8 pts) x(yy′−3)+y2=0
Answers
1. The solution to the first differential equation is given by e^2yx - ysin(xy) + y^2 + C = 0, where C is an arbitrary constant.
2. The general solution to the second differential equation is x(3x - y^2) = C, where C is a positive constant.
To solve the first-order differential equations, let's solve them one by one:
1. (e^2y - ycos(xy))dx + (2xe^2y - xcos(xy) + 2y)dy = 0
We notice that the given equation is not in standard form, so let's rearrange it:
(e^2y - ycos(xy))dx + (2xe^2y - xcos(xy))dy + 2ydy = 0
Comparing this with the standard form: P(x, y)dx + Q(x, y)dy = 0, we have:
P(x, y) = e^2y - ycos(xy)
Q(x, y) = 2xe^2y - xcos(xy) + 2y
To check if this equation is exact, we can compute the partial derivatives:
∂P/∂y = 2e^2y - xcos(xy) - sin(xy)
∂Q/∂x = 2e^2y - xcos(xy) - sin(xy)
Since ∂P/∂y = ∂Q/∂x, the equation is exact.
Now, we need to find a function f(x, y) such that ∂f/∂x = P(x, y) and ∂f/∂y = Q(x, y).
Integrating P(x, y) with respect to x, treating y as a constant:
f(x, y) = ∫(e^2y - ycos(xy))dx = e^2yx - y∫cos(xy)dx = e^2yx - ysin(xy) + g(y)
Here, g(y) is an arbitrary function of y since we treated it as a constant while integrating with respect to x.
Now, differentiate f(x, y) with respect to y to find Q(x, y):
∂f/∂y = e^2x - xcos(xy) + g'(y) = Q(x, y)
Comparing the coefficients of Q(x, y), we have:
g'(y) = 2y
Integrating g'(y) with respect to y, we get:
g(y) = y^2 + C
Therefore, f(x, y) = e^2yx - ysin(xy) + y^2 + C.
The general solution to the given differential equation is:
e^2yx - ysin(xy) + y^2 + C = 0, where C is an arbitrary constant.
2. x(yy' - 3) + y^2 = 0
Let's rearrange the equation:
xyy' + y^2 - 3x = 0
To solve this equation, we'll use the substitution u = y^2, which gives du/dx = 2yy'.
Substituting these values in the equation, we have:
x(du/dx) + u - 3x = 0
Now, let's rearrange the equation:
x du/dx = 3x - u
Dividing both sides by x(3x - u), we get:
du/(3x - u) = dx/x
To integrate both sides, we use the substitution v = 3x - u, which gives dv/dx = -du/dx.
Substituting these values, we have:
-dv/v = dx/x
Integrating both sides:
-ln|v| = ln|x| + c₁
Simplifying:
ln|v| = -ln|x| + c₁
ln|x| + ln|v| = c₁
ln
|xv| = c₁
Now, substitute back v = 3x - u:
ln|x(3x - u)| = c₁
Since v = 3x - u and u = y^2, we have:
ln|x(3x - y^2)| = c₁
Taking the exponential of both sides:
x(3x - y^2) = e^(c₁)
x(3x - y^2) = C, where C = e^(c₁) is a positive constant.
This is the general solution to the given differential equation.
To learn more about derivatives Click Here: brainly.com/question/29144258
#SPJ11