The graph of a function g is shown below.
Use the graph of the function to find its average rate of change from x=-2 to x=4.
Simplify your answer as much as possible.
1-10

Answers
Answer: -2
Step-by-step explanation:
The graph passes through (-2, 3) and (4, -9).
So, the average rate of change is \(\frac{-9-3}{4-(-2)}=\boxed{-2}\)

Related Questions
What is the difference of the polynomials:
(3x2 + 4x + 8) - (2x2 + 2x + 5)
a x^2 + 2x + 3
b x^2 + 6x + 3
c x^4 + 2x^2 + 3
d x^4 + 6x^2 + 13
Answers
Answer:
(6+4x+8)-4-2x-5
6-4+4x-2x+8-5
2+2x+3.
x + 121 = 4x - 20 what is x
Answers
Answer:
x = 47
Step-by-step explanation:
x + 121 = 4x - 20
-3x + 121 = - 20
-3x = -141
x = 47
So, the answer is x = 47
Gravel is being dumped from a conveyor belt at a rate of 15 ft3/hr and its coarseness is such that it forms a pile in the shape of an inverted right cone whose height is three times its base radius. How fast is the height of the pile increasing when the pile has a height of 10 ft
Answers
Answer:
0.43 ft/hr
Step-by-step explanation:
dv/dt = 15ft³/hr
Height = 10ft
We are required to get dh/dt
h = 3r
r = h/3
Formula for volume = 1/3πr²h
We put value of h
1/3π(h/3)²h
= 1/3π(h²/9)h
= 1/3πh³/9
= πh³/29
dv/dt = 1/27π.3h²dh/dt
= dv/dt = πh²/9dh/dt
Remember dv/dt = 15
When we put this in we get
dh/dt = 15x9/3.142x10²
= 135/314.2
= 0.43 ft³/hr
Please check the attachment I added also to add you.

Help plsssssssssssssssssssssss

Answers
Answer:
Step-by-step explanation:
let Garrett orders x stickersfrom each company.
then
30+0.80x=14+1.20x
f(x)=7x+3 and g(x)=-6x-8, find (f•g)(x) and (f•g)(-1)
Answers
Answer:
\((f*g)(x)=-42x^2-74x-24\)
\((f*g)(-1)=8\)
Step-by-step explanation:
\(f(x)=7x+3\\ g(x)=-6x-8\)
\((f*g)(x)=(7x+3)(-6x-8)\\(f*g)(x)=-42x^2-56x-18x-24\\(f*g)(x)=-42x^2-74x-24\)
Now;
\((f*g)(-1)=-42x^2-74x-24\\(f*g)(-1)=-42(-1)^2-74(-1)-24\\(f*g)(-1)=-42(1)+74-24\\(f*g)(-1)=-42+50\\(f*g)(-1)=8\)
In any circle of radius R, how many arcs with lengths R fit into the circumference?

Answers
If we take the radius of a circle be R. Then, we can define that,
$ R = x $
Hence,
Arcs will be as $ 4x $. As,
A circle can be divided into four parts according to the radius.
Hence, we know that,
\(x \times 4\)
\( \mapsto \: 4x\)
Hence, according to the radius R, a circle can have 4 arcs.Nearpod,What is a function questions
Answers
Answer:
A function is a relation for which each value from the set the first components of the ordered pairs is associated with exactly one value from the set of second components of the ordered pair
Step-by-step explanation:
hope this helps!
Step-by-step explanation:
A set of question on the concept of the function in calculus are presented along with their solutions.These question have been designed to help you gain deep understanding of the concept of the function .
PLSSSSSS HELP!!!! TIME LIMITEDDD!!!!!! Joan wants to draw a picture that includes a pair of complementary angles. Joan wants one of the angles to be 18° more than the other angle. Select True or False for each statement about the angles.
The smaller angle is 18°.
The smaller angle is 36°.
The larger angle is 54°.
The larger angle is 72°.
Answers
Answer:
True: The smaller angle is 36°; The larger angle is 54°
False: The smaller angle is 18°. The larger angle is 72°
If you create an equation using this scenario, it would be (18+x)+x=90, because complementary angles sum up to 90°. Add the like terms to get 18+2x=90. Subtract 18 on both sides to get 72. Divide 2 on both sides to result with x=36. Subtract 90 with 36 to get 54. The smaller angle is 36° and the larger angle is 54°.
A professor, transferred from Toronto to New York, needs to sell his house in Toronto quickly. Someone has offered to buy his house for $220,000, but the offer expires at the end of the week. The professor does not currently have a better offer but can afford to leave the house on the market for another month. From conversations with his realtor, the professor believes the price he will get by leaving the house on the market for another month is uniformly distributed between $210,000 and $235,000. If he leaves the house on the market for another month, what is the probability that he will get at least $225,000 for the house
Answers
If the radius of a circle is 2.6 inches, what is the diameter of the circle?
Answers
Answer:
5.2
Step-by-step explanation:
radius is half the diameter
Answer:
5.2in
Step-by-step explanation:
7 2/3-4 1/4 help please
Answers
let's firstly convert the mixed fractions to improper fractions.
\(\stackrel{mixed}{7\frac{2}{3}}\implies \cfrac{7\cdot 3+2}{3}\implies \stackrel{improper}{\cfrac{23}{3}}~\hfill \stackrel{mixed}{4\frac{1}{4}} \implies \cfrac{4\cdot 4+1}{4} \implies \stackrel{improper}{\cfrac{17}{4}} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{23}{3}-\cfrac{17}{4}\implies \cfrac{(4)23~~ - ~~(3)17}{\underset{\textit{using this LCD}}{12}}\implies \cfrac{92~~ - ~~51}{12}\implies \cfrac{41}{12}\implies 3\frac{5}{12}\)
Determine the unknown side length of the right triangle to the nearest hundredth. View the figure.

Answers
In the right triangles whose legs are a, b and its hypotenuse is c
\(a^2+b^2=c^2\)In triangle JLK
∵ LK and JL are the legs of the triangle
∵ KJ is the hypotenuse
\(\therefore(LK)^2+(JL)^2=(KJ)^2\)∵ KL = 14 m and KJ = 18 m
Substitute them in the rule above to find JL
\(\begin{gathered} (14)^2+(JL)^2=(18)^2 \\ 196+(JL)^2=324 \end{gathered}\)Subtract 196 from both sides
\(\begin{gathered} 196-196+(JL)^2=324-196 \\ (JL)^2=128 \end{gathered}\)Take a square root for both sides
\(\begin{gathered} \sqrt[]{(JL)^2}=\sqrt[]{128} \\ JL=11.3137085 \end{gathered}\)Round it to the nearest hundredth
\(\therefore JL=11.31m\)The answer is 11.31 m
Carlos stood outside the park and asked every fourth person to enter the park for their favorite sport. There were four choices: football, baseball, basketball, and other. Bill surveyed a total of 54 people. Of those surveyed, 15 said football is their favorite, 13 said baseball is their favorite, 12 said basketball is their favorite, and 14 said other.
Answers
Answer:
216???
Step-by-step explanation:
54 times 4 bc every fourth person that comes in
I have no Idea tho
the given number line shows the solutions to which inequality
A)x + 4 ≥ 5
B)x – 2 > 7
C)x – 3 ≥ 6
D)x – 1 ≥ 8
—————————-
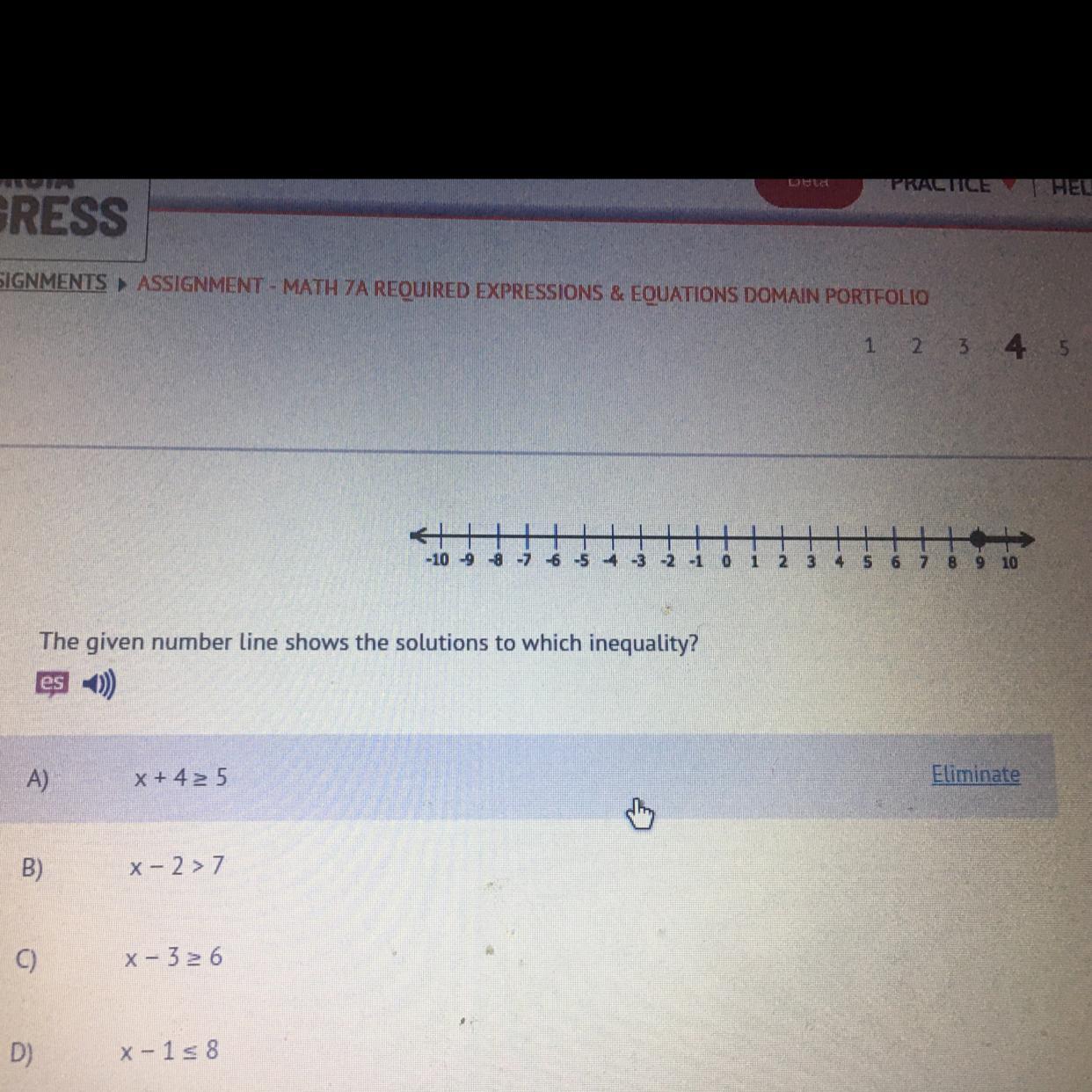
Answers
C) x – 3 ≥ 6
Solving this inequality by adding 3 on both sides, we get
x ≥ 9 which is shown on the number line
I NEED YOUR HELP!! I'LL. GIVE YOU BRAINLIEST

Answers
Answer: ∠16 and ∠11
Step-by-step explanation:
All of these answer options include ∠16, so we know we're looking for an angle that is corresponding to ∠16. A corresponding angle is an angle that is in the same relative position. We will look at ∠9, ∠11, ∠2, and ∠12 since those are the given answer options, and see which is corresponding.
The correct corresponding angles are ∠16 and ∠11.

Point J has coordinates (–3, 4) in the coordinate plane. Point K has coordinates (3, 4). Both points will be reflected across the x-axis.
Answers
The location of the image of points J and K following a reflection across the x-axis are;
J'(-3, -4), and K'(3, -4)Which method can be used to find the image of a point following a reflection?Coordinates of point are;
J(-3, 4), K(3, 4)
The given transformation is; A reflection across the x-axis
The representation of a reflection across the x-axis is presented as follows;
(x, y) → (x, -y)The image of J and K following a transformation across the x-axis are therefore;
J(-3, 4) → J'(-3, -4)K(3, 4) → K'(3, -4)Learn more about reflection transformation on the coordinate plane here:
https://brainly.com/question/8242111
#SPJ1
From the tower of 32meter of heights,a car is observed at angle of the depression of 55 degrees. Find how far the a car from the tower
Answers
the car is approximately 22.4 meters away from the tower.
What is Trigonometric Functions?
Trigonometry uses six fundamental trigonometric operations. Trigonometric ratios describe these operations. The sine function, cosine function, secant function, co-secant function, tangent function, and co-tangent function are the six fundamental trigonometric functions. The ratio of sides of a right-angled triangle is the basis for trigonometric functions and identities. Using trigonometric formulas, the sine, cosine, tangent, secant, and cotangent values are calculated for the perpendicular side, hypotenuse, and base of a right triangle.
we can write:
tan(55 degrees) = 32 / d
To solve for "d", we can rearrange the equation:
d = 32 / tan(55 degrees)
Using a calculator, we can evaluate the tangent of 55 degrees:
tan(55 degrees) = 1.428
d = 22.4 meters
Therefore, the car is approximately 22.4 meters away from the tower.
Learn more about Trigonometric Functions, by the following link.
brainly.com/question/24349828
#SPJ1
Step It Out 12 Find the product. Identify any properties that you used. A. (4)(-0.5)(-3) (-3) Turn Tused the order of operations and multiplied from The product is even / odd. B. (-)(-7X(-9) =) (-)(-9) because the number of negative factors is -O) -00 (3) = -21 89 to I used the the order of the factors, and then I used the Property of Multiplication to group factors to make the multiplication easier. The product is because the number of negative factors is even / odd Property of Multiplication to switch
Answers
The solution to the product is -18 and the property is negative factors
How to determine the productFrom the question, we have the following parameters that can be used in our computation:
(4)(-0.5)(-3) (-3)
Using the property of negative factors, we have
(4)(-0.5)(3) (3)
Next, we remove the brackets
This gives
4 * -0.5 * 3 * 3
Evaluate the product
-18
Hence, the solution is -18
Read more about expression at
https://brainly.com/question/4541471
#SPJ1
A company asks an investor for an investment of $800,000 in exchange for 15% equity in the business. What is the implied valuation of the business?
Answers
If a company asks an investor for an investment of $800,000 in exchange for 15% equity in the business. The implied valuation of the business is: $4,533,333.
Implied valuationFirst step is to calculate the equity valuation
Using this formula
Equity valuation=Amount invested/Equity rate
Let plug in the formula
Equity valuation=$800,000/.15
Equity valuation=$5,333,333
Second step is to calculate the implied valuation
Implied valuation=Equity valuation-Amount invested
Let plug in the formula
Implied valuation=$5,333,333-$800,000
Implied valuation=$4,533,333
Therefore If a company asks an investor for an investment of $800,000 in exchange for 15% equity in the business. The implied valuation of the business is: $4,533,333.
Learn more about implied valuation here:https://brainly.com/question/13258604
#SPJ1
A student is using the elimination method to solve the system of equations below. What is the best first
step?
4x - 5y = 2
2x + y = -3
Answers
Answer:
The best first step would be to multiply the second equation by -2
Step-by-step explanation:
The best first step would be to multiply the second equation by -2
then you would have the following
\(\ \ \ \ \ \ 4x - 5y = 2 \\-2*(2x)+ (-2)*y = (-2)*3\)
and when you multiply it is easy to eliminate because you will get
\(4x - 5y = 2 \\-4x -2y = 6\)
and if you sum the equations you get
-7y = 8
so that is a single variable equation which is easier to solve.
Describe in words the transformations of the graph of the parent function f(x) = x2 that
would result in the graph of
g(x) = 3(x - 5)^2 + 2.
Describe in words the transformations of the graph of the parent function f(x) = x2 that
would result in the graph of
g(x) = 1/3(x + 6)^2- 4.

Answers
2. The transformations are given as follows:
Vertical stretch by a factor of 3.Translation right 5 units.Translation up 2 units.3. The transformations are given as follows:
Vertical compression by a factor of 3.Translation left 6 units.Translation down 4 units.How to define the transformations?For item 2, the transformations in this problem are given as follows:
Vertical stretch by a factor of 3, due to the multiplication by 3.Translation right 5 units, as x -> x - 5.Translation up 2 units, as y -> y + 2.For item 3, the transformations are given as follows:
Vertical compression by a factor of 3, due to the multiplication by 1/3.Translation left 6 units, as x -> x + 6.Translation down 4 units, as y -> y - 4.More can be learned about translations at brainly.com/question/28174785
#SPJ1
Use ALL of the tools have, to find area and perimeter of this below:

Answers
9514 1404 393
Answer:
area 36 ft²perimeter 30 ftStep-by-step explanation:
The area can be decomposed into a rectangle and a trapezoid.
The rectangle is 2' by 5', so has area ...
A = LW
A = (5 ft)(2 ft) = 10 ft²
The trapezoid has bases 8 ft and 5 ft, and height 4 ft, so its area is ...
A = 1/2(b1 +b2)h
A = 1/2(8 ft +5 ft)(4 ft) = 26 ft²
Then the total area of the figure is ...
total area = 10 ft² +26 ft² = 36 ft²
__
The slant side of the trapezoid is the hypotenuse of a triangle with sides 3 and 4. The Pythagorean theorem tells us its length is ...
c = √(a² +b²) = √(3² +4²) = √25 = 5
The perimeter of the figure is the sum of the side lengths. Working clockwise from the top, that sum is ...
P = 5 + 4 + 2 + 2 + 5 + 2 + 5 + 5 = 30 . . . feet
The perimeter of the figure is 30 feet.

The base area of a right circular cone is 1/4 of its total surface area. What is the ratio of the radius
to the slant height?
Answers
Given:
The base area of a right circular cone is \(\dfrac{1}{4}\) of its total surface area.
To find:
The ratio of the radius to the slant height.
Solution:
We know that,
Area of base of a right circular cone = \(\pi r^2\)
Total surface area of a right circular cone = \(\pi rl+\pi r^2\)
where, r is radius and l is slant height.
According to the question,
\(\pi r^2=\dfrac{1}{4}(\pi rl+\pi r^2)\)
Multiply both sides by.
\(4\pi r^2=\pi rl+\pi r^2\)
\(4\pi r^2-\pi r^2=\pi rl\)
\(3\pi r^2=\pi rl\)
Cancel out the common factors from both sides.
\(3r=l\)
Now, ratio of the radius to the slant height is
\(\dfrac{r}{l}=\dfrac{r}{3r}\)
\(\dfrac{r}{l}=\dfrac{1}{3}\)
Therefore, the ratio of the radius to the slant height is 1:3.
The equation c = 8m represents how many ice cream cones (c) are sold within a certain number of minutes (m) at a certain ice cream shop.
Determine the constant of proportionality.
8
1
one-eighth
16
Answers
The constant of proportionality in the equation c = 8m is 8.
What is a variation?A variation is a relation between a set of values of one variable and a set of values of other variables. Direct variation. In the equation y = mx + b, if m is a nonzero constant and b = 0, then you have the function y = mx (often written y = kx), which is called a direct variation.
since C = 8m is an equation and the relationship between c and m is direct.
It means that dividing both sides of the equation by m we have
C/m = 8m/m
c/m = 8
Therefore the constant of proportionality is 8
In conclusion the constant of proportionality for which c = 8m is 8.
Learn more about variation: https://brainly.com/question/6499629
#SPJ1
Type the correct answer in each box.
Day Amount
1
$26
2
$23
3
$31
4
$26
5
534
The table shows the amount Bill spent on 5 days last week.
The mean of the amount he spent is $
The mean absolute deviation is $
Reset
Next
Answers
The mean absolute deviation is $106.6.
Given the table shows the amount Bill spent on 5 days last week.
DayAmount12622313126534To find the mean of the amount he spent: The formula for calculating the mean of a given set of values is mean=∑x/n where x represents the values, n represents the number of values, and ∑x represents the sum of the values.
Mean=total sum of values/total number of values Mean=(26+23+31+26+534)/5Mean=640/5Mean=128So,
the mean of the amount he spent is $128.To find the mean absolute deviation: The mean absolute deviation (MAD) is the average distance between each data value and the mean. MAD shows how much the data set deviates from the mean. The formula for calculating the MAD is MAD=∑|xi−m|/n where xi represents the values, m represents the mean, and n represents the number of values. So, the calculation for each day is:
Day Amount Absolute deviation from mean1 26 |128-26|=102 23 |128-23|=105 31 |128-31|=974 26 |128-26|=102 534 |128-534|=406
The sum of all absolute deviations is:
10+10+97+10+406=533The mean absolute deviation (MAD) is: MAD=533/5=106.6So.
For more question deviation
https://brainly.com/question/475676
#SPJ8
simplify [Xn (X'nY)]'.
Answers
Answer:
(X'U'Y) + (XUY')
Step-by-step explanation:
Starting with [Xn(X'nY)]', we can use De Morgan's laws to simplify the expression:
[Xn(X'nY)]' = (Xn)' + (X'nY)'
Recall that Xn represents the logical operator "and", while X' represents "not X". Using these definitions, we can expand the expression:
(Xn)' + (X'nY)' = (X'U'Y) + (XUY')
where U represents the logical operator "or".
Therefore, [Xn(X'nY)]' simplifies to (X'U'Y) + (XUY').
A box measures 4 inches by 2 inches by 6 inches .Find the volume of the box in cubic centimeters
Answers
Answer:
121.92 cm cubed
Step-by-step explanation:
all you have to do is multiply all 3 measurements to find the simple shapes volume, and then convert to centimeters using the simple 2.54 cm=1 in conversion rate
Answer:
1/36 cubic ft
Step-by-step explanation:
4 inches = 12/3 inches = 1/3 ft
2 inches = 12/6 inches = 1/6 ft
6 inches = 12/2 inches = 1/2 ft
Finding trigonometric ratios from a point on the unit circle

Answers
The terminal side of theta intersects with unit circle at (-√2/2, -√2/2)
The only quadrant where we have (-, -), that is the y and x coordinate is negative is the third quadrant
In the third quadrant: tan is positive, cos is negative and sine is negative
from the point of the unit circle:
\(\begin{gathered} x\text{ = adjacent = }\frac{-\sqrt[]{2}}{2} \\ y\text{ = opposite = }\frac{-\sqrt[]{2}}{2} \\ \text{hypotenuse}^2=opposite^2+adjacent^2 \\ \text{hypotenuse}^2=\text{ }(\frac{-\sqrt[]{2}}{2})^2\text{ + }(\frac{-\sqrt[]{2}}{2})^2 \\ \text{hypotenuse}^2=\frac{2}{4}\text{ + }\frac{2}{4}\text{ = }\frac{4}{4}=\text{ 1} \\ \text{hypotenuse = }\sqrt[]{1} \\ \text{hypotenuse = 1} \end{gathered}\)We can find csc θ, sin θ and cot θ now:
\(\begin{gathered} co\sec \text{ }\theta\text{ = }\frac{1}{\sin \text{ }\theta} \\ \sin \text{ }\theta\text{ = }\frac{opposite}{hypotenuse} \\ \sin \theta\text{= }\frac{\frac{-\sqrt[]{2}}{2}}{1}\text{ = }\frac{-\sqrt[]{2}}{2} \\ \\ co\sec \text{ }\theta\text{ = }\frac{1}{\frac{-\sqrt[]{2}}{2}}\text{ = 1 }\div\text{ }\frac{-\sqrt[]{2}}{2}\text{ = 1 }\times\text{ }\frac{2}{-\sqrt[]{2}} \\ co\sec \text{ }\theta\text{ = }\frac{2}{-\text{ }\sqrt[]{2}} \end{gathered}\)\(\begin{gathered} \sin \theta\text{ = }\frac{opposite}{\text{hypotenuse}} \\ \sin \theta\text{ = }\frac{-\text{ }\sqrt[]{2}}{2} \end{gathered}\)\(\begin{gathered} \cot \theta\text{ = }\frac{1}{\tan\theta\text{ }} \\ \tan \text{ }\theta\text{ = }\frac{\sin\theta}{\cos\theta} \\ \\ \cos \text{ }\theta\text{ = }\frac{adjacent}{\text{hypotenuse}} \\ \cos \text{ }\theta\text{ = }\frac{\frac{-\sqrt[]{2}}{2}}{1}\text{ = }\frac{-\sqrt[]{2}}{2} \\ sin\text{ }\theta\text{ = }\frac{-\sqrt[]{2}}{2} \\ \\ \tan \text{ }\theta\text{ = }\frac{\frac{-\sqrt[]{2}}{2}}{\frac{-\sqrt[]{2}}{2}}\text{ = 1} \\ \cot \theta=\frac{1}{1} \\ \cot \theta\text{ = 1} \end{gathered}\)In the figure at the right, RS is extended as shown. Find m/QSR.
A 26°
B 34°
C 50°
D 96°
34°
Q
(4x-8)° (76-x)°
S
R
(Number8) I really need this pls

Answers
The value of angle QSR is determined as 50⁰.
What is the value of angle QSR?The value of angle QSR can be obtained if we calculate the value of x.
The value of x is calculated by setting up the following equation as shown below;
(4x - 8) + 34 + (76 - x) = 180 (sum of angles in a straight line )
4x - 8 + 34 + 76 - x = 180
3x = 180 - 102
3x = 78
x = 78/3
x = 26
The value of angle QSR;
∠QSR = 76 - x
∠QSR = 76 - 26
∠QSR = 50⁰
Learn more about angle on straight line here: https://brainly.com/question/164801
#SPJ1
3. Prepare a contribution margin income statement.
Naomi's Quilt Shoppe sells homemade Amish quilts. Naomi buys the quilts from local
Amish artisans for $290 each, and her shop sells them for $490 each. She also pays a
sales commission of 8% of sales revenue to her sales staff. Naomi leases her country-
style shop for $1,300 per month and pays $1,800 per month in payroll costs in addition
to the sales commissions. Naomi sold 95 quilts in February,
Answers
According to Naomi's Quilt Shoppe's contribution margin income statement, she had a net income of $12,176 for the month of February.
To solve this problemFor the month of February, Naomi's Quilt Shoppe's contribution margin income statement is as follows:
Revenue from Sales: 95 x $490 = 46,550
Cost of Goods Sold: 95 x $290 = $27,550
Gross profit: $27,550 - $46,550 = $19,000.
Variable expenses :
Revenue Commission: 8% × $46,550 = $3,724
Costs for all variables: $3,724
Contribution Margin: $19,000 - $3,724 = $15,276
Fixed expenses :
Rent: $1,300
Cost of payroll: $1,800
Total Fixed Costs: $3,100
Net Income: $15,276 - $3,100 = $12,176
Therefore, According to Naomi's Quilt Shoppe's contribution margin income statement, she had a net income of $12,176 for the month of February.
Learn more about multiply here : brainly.com/question/29120629
#SPJ1