Steven throws a dart at a dartboard with radius 9 inches. Suppose that the dart lands randomly on the dartboard at a point with distance R from the center of the dartboard. Find the probability P(R sr) that the distance from the center is less than r for r > 0. [Hint: compare the area of the event R Sr to the total area of the dartboard). Suppose that the bullseye is a circular region with radius 1 inch at the center of the dartboard. Find the probability that the dart lands in the bullseye.
Answers
To find the probability P(R < r), we need to compare the area of the event R < r (i.e. the circle with radius r centered at the center of the dartboard) to the total area of the dartboard.
The total area of the dartboard is π(9)^2 = 81π square inches. The area of the circle with radius r is πr^2. So the probability that the distance from the center is less than r is:
P(R < r) = (area of circle with radius r) / (total area of dartboard)
P(R < r) = πr^2 / (81π)
P(R < r) = r^2 / 81
To find the probability that the dart lands in the bullseye, we need to compare the area of the bullseye to the total area of the dartboard.
The area of the bullseye is π(1)^2 = π square inches. So the probability that the dart lands in the bullseye is:
P(dart lands in bullseye) = (area of bullseye) / (total area of dartboard)
P(dart lands in bullseye) = π / (81π)
P(dart lands in bullseye) = 1/81
we'll need to consider the areas of the dartboard and the event R ≤ r, as well as the bullseye.
The total area of the dartboard (A_total) is given by the formula for the area of a circle: A_total = π(radius)^2 = π(9 inches)^2 = 81π square inches.
Now let's find the probability P(R ≤ r) for r > 0. The area of this event (A_event) is also given by the area of a circle: A_event = π(r)^2. To find the probability, we'll compare A_event to A_total:
P(R ≤ r) = A_event / A_total = (π(r)^2) / (81π).
The π terms cancel out, leaving us with:
P(R ≤ r) = r^2 / 81.
For the bullseye, it has a radius of 1 inch. We can use the same probability formula:
P(bullseye) = r^2 / 81 = (1 inch)^2 / 81 = 1 / 81.
So the probability that the dart lands in the bullseye is 1/81.
Visit here to learn more about probability : https://brainly.com/question/30034780
#SPJ11
Related Questions
we are interested in testing to see if the variance of a population is less than 5. the correct null hypothesis is σ< 5. σ< 25. σ^2 ≥ 5. σ^2 ≥ 25.
Answers
The variance of a population is less than 5. Null hypothesis reflects the initial presumption or claim that something is true in this case and true option is : σ^2 ≥ 5.
In hypothesis testing, the null hypothesis (H0) represents the assumption or claim that is initially presumed to be true. In this scenario, we are interested in testing whether the variance of the population is less than 5.
The notation σ^2 represents the population variance, and the symbol ≥ denotes "greater than or equal to." Therefore, the correct null hypothesis is that the population variance is greater than or equal to 5 (σ^2 ≥ 5).
The other options listed are not correct for this scenario:
- σ < 5: This alternative hypothesis suggests that the population variance is strictly less than 5, which is not the hypothesis we want to test.
- σ < 25: This alternative hypothesis suggests a different value for the population variance, which is not what we are interested in.
- σ^2 ≥ 25: This alternative hypothesis sets a higher threshold for the population variance, which is not the hypothesis we want to test.
Therefore, the correct null hypothesis is σ^2 ≥ 5, indicating that the population variance is greater than or equal to 5.
To know more about null hypothesis refer here:
https://brainly.com/question/30821298?#
#SPJ11
help pls 20 points due today

Answers
Answer: A
Step-by-step explanation:
Solve the system using any method:
y = x - 3
y = 7x + 3
Answers
Answer:
x=-1, y=-4
Step-by-step explanation:
For this question, you can replace y in one equation with the second one.
This means x-3=7x+3.
From there, you subtract x from each side, giving -3=6x+3.
Subtracting 3 from each side makes it -6=6x.
Dividing both sides by 6 leaves x isolated, with a result of x=-1.
You can substitute the value of x into either equation to work out y. I'm using the first one, as it has smaller numbers.
This equation is now y=-1-3, which can be solved for y=-4.
**This content involves simultaneous equations, which you may wish to revise. I'm always happy to help!
Which pair shows equivalent expressions?

Answers
Answer:
2(2/5x+2)=4x/5+4
Step-by-step explanation:
2(2/5x+2)=4x/5+4
4x/5 +4=4x/5 +4
someone help me on this offering 100 points hurry please

Answers
Answer:
From my calculations I'm not sure if I'm right but I got 14.2
If it's not right my apologies
a⃗ =⟨−1,−4⟩ and b⃗ =⟨3,2⟩.
Represent a⃗ −b⃗ using the head-to-tail method.
Use the Vector tool to draw the vectors, complete the subtraction by the head-to-tail method, and draw a⃗ −b⃗ .
To use the Vector tool, select the initial point and then the terminal point.
Answers
The resultant of the vector subtraction of vector a and vector b is determined as ( -4, - 6).
What is the resultant of the vector addition?The resultant of the vector subtraction is calculated as follows;
The given vector expression;
a = ( -1, - 4) and b = (3, 2 )
Then the subtraction of the two vector is calculated as follows;
a - b = ( -1, -4 ) - (3, 2 )
To subtract each component of the vector, we will simply collect similar terms, for example, vectors in x direction will be subtracted and the vectors in y direction will be subtracted as well.
( -1, -4 ) - (3, 2 ) = ( -1 - 3, -4-2)
R = ( -4, - 6)
The vector diagram is in the image attached.
Learn more about subtraction of two vectors here: https://brainly.com/question/14920537
#SPJ1

Viết phương trình đường thẳng biết
a) vuông góc với đường thẳng x+2y=1 và đi qua A(1;2)
b) đi qua gốc toạ độ và đi qua điểm M (-1;3)
Answers
Answer:
Step-by-step explanation:
a) 2x - y = 0
16+ n/4 =22
Help me solve please and thank you :))
Answers
Answer:
n = 24
Step-by-step explanation:
16+ n/4 =22
Subtract 16 from each side
16-16+ n/4 =22-16
n/4 = 6
Multiply each side by 4
n/4*4 = 6*4
n = 24
Elle sews fleece baby blankets, and each blanket requires 3 ft. of material. She has 52 ft. of fleece in her workshop and would like to make at least 16 blankets. Write an inequality that represents how many blankets Elle can make in her workshop
Answers
The final inequality that represents how many blankets Elle can make in her workshop would be:
3x ≤ 52 and x ≥ 16
What is Inequality ?In mathematics, an inequality is a statement that compares two values or expressions using an inequality symbol such as "<" (less than), ">" (greater than), "<=" (less than or equal to), ">=" (greater than or equal to), or "≠" (not equal to).
An inequality indicates that one value or expression is smaller, greater, or not equal to the other value or expression.
The inequality "y <= 10" states that the value of "y" is less than or equal to 10.
Let "x" be the number of blankets Elle can make in her workshop.
Since each blanket requires 3 ft. of material, the total amount of fleece required for "x" blankets would be 3x ft.
We know that Elle has 52 ft. of fleece in her workshop, so we can set up the inequality:
3x ≤ 52
This inequality states that the amount of fleece required for "x" blankets must be less than or equal to the amount of fleece Elle has available.
To satisfy the condition of making at least 16 blankets, we can add the requirement that "x" must be greater than or equal to 16.
To know more about expressions visit:
https://brainly.com/question/1859113
#SPJ1
HELPPPPPPP PLSSSSSS!!!!!!!!

Answers
Simplify fully12xy24xy
Answers
Answer:
288xy
Step-by-step explanation:
First, you multiply 12 by 24 and you get 288. Next, you can't forget the variables, so you add those to the end and get, 288xy.
find an equation of the plane. the plane through the point (−2, 7, 10) and perpendicular to the line x = 3 t, y = 4t, z = 3 − 4t
Answers
As per the details given, the equation of the plane passing through the point (−2, 7, 10) and perpendicular to the line x = 3t, y = 4t, z = 3 − 4t is 3x + 4y - 4z + 18 = 0.
We require a point on the plane and the normal vector to the plane in order to find the equation of the plane. On the plane, the specified point (2, 7, 10) is located. We must now locate the normal vector.
The parametric form of the line x = 3t, y = 4t, and z = 3 4t. This line's direction vector is [3, 4, -4]. Use the direction vector of the line as the normal vector in order to get the normal vector to the plane.
3(x + 2) + 4(y - 7) - 4(z - 10) = 0
3x + 6 + 4y - 28 - 4z + 40 = 0
3x + 4y - 4z + 18 = 0
Thus, the equation of the plane passing through the point (−2, 7, 10) and perpendicular to the line x = 3t, y = 4t, z = 3 − 4t is 3x + 4y - 4z + 18 = 0.
For more details regarding parametric form, visit:
https://brainly.com/question/30790157
#SPJ1
PLEASE HELP
percent to the nearest inwalreden of a pertent? 11.969.39 9804011 \( 511,61+32 \) ?
Answers
Rounding a percentage to the nearest whole number can be done by considering the decimal part of the percentage. For the percentages provided, 11.969 would round to 12%, 39.9804 would round to 40%, and 11.61+32 would equal 43.
To round a percentage to the nearest whole number, we examine the decimal part. If the decimal is 0.5 or greater, we round up to the next whole number. If the decimal is less than 0.5, we round down to the previous whole number. In the given examples, 11.969 has a decimal of 0.969, which is closer to 1 than to 0, so it rounds up to 12. Similarly, 39.9804 has a decimal of 0.9804, which is closer to 1, resulting in rounding up to 40. Lastly, the expression 11.61 + 32 equals 43, as it is a straightforward addition calculation.
To know more about round a percentage here: brainly.com/question/29096182
#SPJ11
Calculate the area of the triangle? What is the best way to solve it

Answers
Answer: Find the the height and length of the triangle. I'm not sure what it would be but then use a1 + a2 to find the area
Answer:
Formula of triangle: A = 1/2 x b x h
Step-by-step explanation:
Solve the base of the triangle by solving the distance between points (-2,0) and (f, -5) in units, and then do the same for height: find distance between points (-2, 6) and (-2, 0). Once you find the distance, input value of base and height into the formula and solve to get the area!
find the value of x plzzzzzz...

Answers
Answer:
x = 120°( if given triangle is equilateral triangle)
Hope this will help you.
The following table represents the highest educational attainment of all adultresidents in a certain town. If a resident who has a master's degree is chosen atrandom, what is the probability that they are aged 40 or over? Round your answer tothe nearest thousandth.

Answers
The answer is: 0.0362
The total number of Master's degree holders = 2848 (from the question)
In order to choose people 40 and above from this Master's degree holder subset,
You choose:
People 40-49 AND People 50 and over.
Number of people 40-49 = 475
Number of people 50 and over = 699
But we also need to take into consideration, the probability of picking a person 40-49 years old OR 50 and over
total Number of people 40 - 49 are 3518
The total Number of people 50 and above are 6518
Thus, we can write the probability as:
\(\begin{gathered} P(\text{choosing 40-49)=}\frac{475}{3518} \\ P(\text{choosing 50 and above)=}\frac{699}{6518} \\ P(choo\sin g\text{ Master's degre}e)=\frac{2848}{19076} \\ \\ \text{Thus, for choosing 40-49 AND Master's degre}e\colon \\ P(\text{choosing 40-49 AND Master's degr}ee)=\frac{475}{3518}\times\frac{2848}{19076}=0.0202 \\ \\ \text{For choosing 50 and above AND Master's degre}e\colon \\ P(\text{choosing 50 and above AND Master's degree)=}\frac{699}{6518}\times\frac{2848}{19076}=0.016 \\ \\ \text{Thus choosing Master's degree holder, 40 or over:} \\ P(\text{choosing 40-49 AND Master's degr}ee)+ \\ P(\text{choosing 50 and above AND Master's degree)} \\ =0.0202+0.016=0.0362 \end{gathered}\)The final answer is: 0.0362
Hi, when i put Pi/2 +Pi/4 it used to give me the answer as 3pi/4 while now it give me 2.35619449 how can i fix it to give me the way i like it again ?
Note i tries pressing on S>D it is not working too!
please help me!!!
Answers
To fix the issue where the expression "π/2 + π/4" is giving you a decimal value instead of the desired fraction, If the "S>D" (standard to decimal) button on your calculator is not working, it might be due to a different labeling or functionality on your particular device.
The decimal value you are seeing, 2.35619449, is the approximate numerical evaluation of the expression "π/2 + π/4." This occurs when your calculator or mathematical software is set to display results in decimal form instead of fractions. If you prefer to see the answer as a fraction, you can change the settings on your calculator or software.
Look for a mode or setting that allows you to switch between decimal and fraction representation. It may be labeled as "Frac" or "Exact" mode. By enabling this setting, the result will be displayed as a fraction, which in this case should be "3π/4" (or equivalently, "π/4 + π/2"). Be sure to consult the user manual or help documentation for your specific calculator or software to locate and adjust the appropriate setting.
If the "S>D" (standard to decimal) button on your calculator is not working, it might be due to a different labeling or functionality on your particular device. Try exploring the settings menu or consult the user manual for further guidance on how to switch from decimal to fraction mode.
Learn more about mathematical software here:
https://brainly.com/question/28475549
#SPJ11
Use the Law of Sines to find each missing side or angle. Round to the nearest tenth.

Answers
Applying the sine rule the value of side x is calculated to be 7.4
How to find the size of xThe size of x is calculated using the sine rule which sates that the ratio of a side and the opposite angles are equal to each other
This represented by the formula
Sine A / a = Sine B / b = Sine C / c
applying the formula for the problem
Sine A / a = Sine B / b
Sine 29 / 5 = Sine 46 / x
cross multiplying
x = 5 * Sine 46 / Sine 29
x = 7.4188
x = 7.4 to the nearest tenth
Learn more about sine rule at:
https://brainly.com/question/27174058
#SPJ1
Answer:
7.4
Step-by-step explanation:
yes
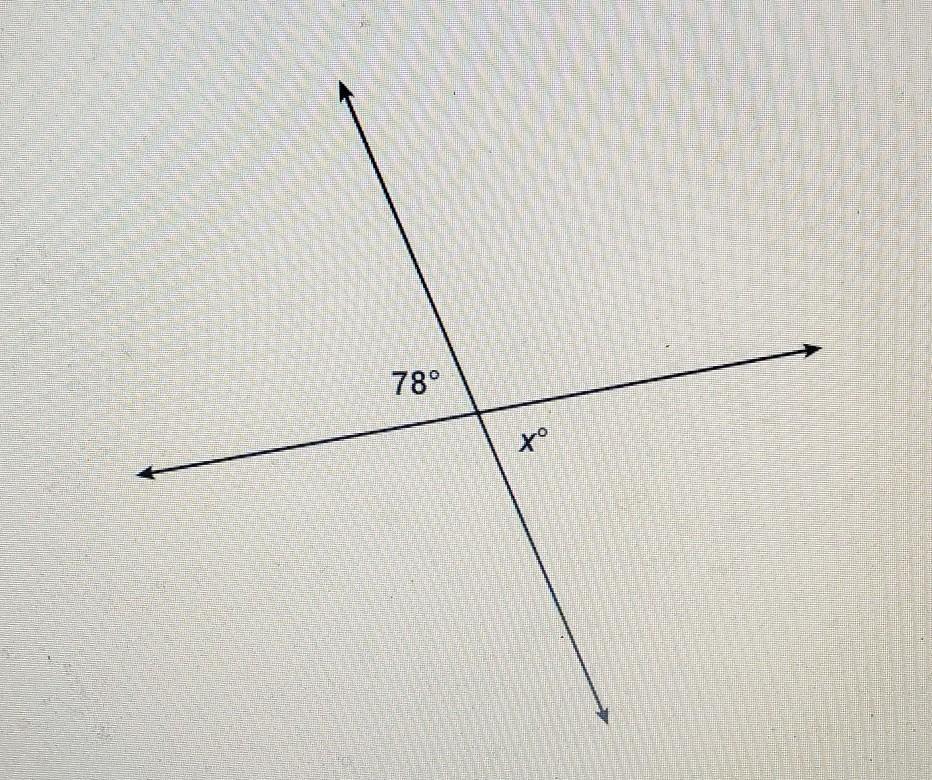
What is the value of x? Enter your answer in the box. X= 78°
Answers
the angles 78° and x° are opposite by vertex then have the same value
\(x=78\)As the prize in a contest, you are offered $29,000 now or $51,000 in 6 years. If the money can be invested at 9% compounded annually, which prize will be worth more in 6 years? Choose the option that is most profitable after 6 years. O accepting the $29,000 prize now O accepting the $51,000 prize in 6 years
Answers
If the money can be invested at 9% compounded annually, then accepting the $51,000 prize in 6 years is the most profitable option after 6 years.
First, let's calculate the future value of the $29,000 prize if it is invested at 9% annual compounded rate for 6 years. We can use the formula FV = PV * (1 + r)^n, where FV is the future value, PV is the present value, r is the annual interest rate, and n is the number of compounding periods. In this case, PV is $29,000, r is 9%, and n is 6. Plugging these values into the formula, we get FV = $29,000 * (1 + 0.09)^6 = $49,193.29.
Now, let's calculate the future value of the $51,000 prize if it is received in 6 years. We already know that the money can be invested at 9% annual compounded rate for 6 years. So, we can directly use the formula FV = PV * (1 + r)^n. In this case, PV is $51,000, r is 9%, and n is 6. Plugging these values into the formula, we get FV = $51,000 * (1 + 0.09)^6 = $86,929.63.
Comparing the future values of both options, we can see that accepting the $51,000 prize in 6 years is more profitable as it will result in a future value of $86,929.63, which is higher than the future value of $49,193.29 that would result from investing the $29,000 prize now.
In conclusion, if the money can be invested at 9% compounded annually, then accepting the $51,000 prize in 6 years is the most profitable option after 6 years. It is important to note that this decision is based solely on financial considerations, and other non-financial factors may also be relevant when making such decisions.
For more such questions on Prize-Profit Comparison.
https://brainly.com/question/14850973#
#SPJ11
PLEASE HELP I WILL GIVE 20

Answers
Answer:
80°
Step-by-step explanation:
since 4x+5x=180, it means that x is 20.
to find SVW, you multiply 4 by 20 which is 80°
write and equation that would create the graph of the line

Answers
we have two points (x, y): (0,1) and (1,3)
We can use the point-slope form
(y - y1) = m (x -x1)
The slope = m= (y2-y1)/ (x2-x1)
or
The slope-intercept form.
y = mx + b
m= (y2-y1)/ (x2-x1)
y-intercept is (0, b)
__________________________
Using The slope-intercept form,
y = mx + b
b = 1
point (0,1)
Replacing
y = mx + 1
finding the slope
point 1 (0, 1), x1= 0; y1= 1
point 2 (1, 3); x2= 1; y2= 3
m= (y2-y1)/ (x2-x1)
Replacing
m= ( 3- 2)/ (1 - 0) = 2/1 = 2
___________________
Replacing the slope
y = 2x + 1
__________________
Answer
y = 2x + 1
if y varies directly as x, and y is 20 when x is 4, what is the constant of variation for this relation?
Answers
Answer:
k = 5
Step-by-step explanation:
Given y varies directly as x then the equation relating them is
y = kx ← k is the constant of variation
To find k use the condition y = 20 when x = 4, then
20 = 4k ( divide both sides by 4 )
5 = k
Answer:
The value of k = 5
Step-by-step explanation:
We know when y varies directly as x, we get the equation
y ∝ x
y = kx
Here 'k' is the 'constant' of proportionality
Given
y = 20, when x = 4so substituting y = 20, x = 4 in the equation y = kx
y = kx
20 = k(4)
k = 20 / 4
k = 5
Therefore, the value of k = 5
A) y=1/3x-8
B) y=1/3x-4
C) y=1/3x+2
D) y=1/3x-14

Answers
Answer:
A
Step-by-step explanation:
Concept :-
The slope intercept form of a line is y = mx + c Where m is slope , and c is constant .On converting :-
\(\bf\implies y + 5 =\dfrac{1}{3}(x-9)\\\\\bf\implies y + 5 =\dfrac{1}{3}x - 3 \\\\\bf\implies y = \dfrac{1}{3}x - 3 - 5 \\\\\bf\implies\boxed{\red{y = \dfrac{1}{3}x -8 }}\)
Hence option A is correct.
Evaluate the following formula for the values given A=p(1+(r)/(n))^(nt) when p=100,r=0.04,n=1,t=3 (the compound interest formula ). The answer is (Type an integer or decimal rounded to the nearest hun
Answers
The final amount A, after three years of compounding at an interest rate of 4% per year, starting with an initial principal amount of $100, is approximately $112.49.
The compound interest formula, A =\(p(1 + r/n)^{(nt)\), calculates the final amount A accumulated from an initial principal amount p over a specified period of time t, with an interest rate of r compounded n times per year.
In this case, we are given p = 100, r = 0.04, n = 1, and t = 3. Substituting these values into the formula, we have:
A = 100(1 + 0.04/1)⁽¹⁾⁽³⁾
Simplifying the expression inside the parentheses first, we have 0.04/1 = 0.04, and 1 + 0.04 = 1.04. Thus, we have:
A = 100(1.04)³
Evaluating the exponent, we get (1.04)³ ≈ 1.124864.
Finally, multiplying 100 by 1.124864, we find that A is approximately equal to 112.4864.
Rounding this value to the nearest hundredth, we obtain A ≈ 112.49.
Therefore, the final amount A, after three years of compounding at an interest rate of 4% per year, starting with an initial principal amount of $100, is approximately $112.49.
Learn more about Compound Interest Formula at
brainly.com/question/29639856
#SPJ4
EB and DA are diameters of circle Y. What is the measure of arc EDC?

Answers
Answer:
Option (D). 110°
Step-by-step explanation:
Since EB and AD are diameter,
\(m(\widehat{ECB})\) = \(m(\widehat{ACD})\) = 180°
\(m(\widehat{ECB})=m(\widehat{EDC})+m(\widehat{BC})\) = 180° -------(1)
And \(m(\widehat{ACD})=m(\widehat{AB})+m(\widehat{BCD})\)
180° = 40° + \(m(\widehat{BCD})\)
\(m(\widehat{BCD})\) = 140°
Since, \(m(\widehat{BCD})=m(\widehat{BC})+m(\widehat{CD})\)
\(2m(\widehat{BC})\) = 140° [Given \(m(\widehat{BC})=m(\widehat{CD})\)]
\(m(\widehat{BC})\) = 70°
From equation (1),
\(m(\widehat{EDC}})\) = 180° - \(m(\widehat{BC})\)
\(m(\widehat{EDC}})\) = 180°- 70°
Therefore, measure of arc(EDC) = 110°
Option (D) will be the answer.
1. An automobile dealer decides to select a month for its annual sale.
A) Find the probability that it will be September or October. Assume all months have an equal probability of being selected.
B) Compute the probability of selecting September or October, using days, and
compare the answer with the answer from part a.
Answers
A) the probability that the month selected for the annual sale will be September or October is 1/6.
How to determine the probabilitiesA) Since we are interested in the probability of selecting September or October, which are two out of the 12 months, the probability can be calculated as:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 2 months / 12 months
Probability = 1/6
Therefore, the probability that the month selected for the annual sale will be September or October is 1/6.
B) To calculate the probability, we need to sum the number of days in September and October and divide it by the total number of days in a year (365 or 366 in a leap year).
Probability = (30 + 31) days / 365 or 366 days
Probability ≈ 61/365 or 366
The exact probability will depend on whether it is a leap year or not.
Comparing the answers from part A and part B, we can see that the probability of selecting September or October using days is slightly different from the probability calculated assuming each month has an equal probability of being selected.
Learn more about probability at https://brainly.com/question/13604758
#SPJ1
consider two random variables x and y with joint pmf given by pxy(k,l)=12k l,for k,l=1,2,3,... show that x and y are independent and find the marginal pmfs of x and y. find p(x2 y2≤10)
Answers
Answer:
Step-by-step explanation:
To show that X and Y are independent, we need to check that their joint PMF factorizes into the product of their marginal PMFs, i.e., PXY(k,l) = PX(k)PY(l) for all k,l.
To do this, we need to find the marginal PMFs of X and Y. We can do this by summing over all possible values of the other variable, as follows:
PX(k) = ∑l=1,2,3,... PXY(k,l) = ∑l=1,2,3,... 1/(2^(k+l))
if sin a=3/5 and sin b= 5/13, where A is an acute angle, B is an obtuse angle. find sin (a+b)
Answers
Answer:
-16/65
Step-by-step explanation:
We can use the sum formula for sine to find sin(a+b):
sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
We are given the values of sin(a) and sin(b), but we don't have the values of cos(a) and cos(b). However, we can use the Pythagorean identity to find them:
sin^2(a) + cos^2(a) = 1 => cos^2(a) = 1 - sin^2(a)
sin^2(b) + cos^2(b) = 1 => cos^2(b) = 1 - sin^2(b)
We know that angle A is acute, so cos(a) is positive. For angle B, we know that it is obtuse, which means that cos(b) is negative. With this information, we can find the values of cos(a) and cos(b):
cos(a) = sqrt(1 - sin^2(a)) = sqrt(1 - (3/5)^2) = 4/5
cos(b) = -sqrt(1 - sin^2(b)) = -sqrt(1 - (5/13)^2) = -12/13
Now we can substitute these values into the sum formula for sine:
sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
= (3/5)(-12/13) + (4/5)(5/13)
= -36/65 + 20/65
= [-16/65]
Help meh plzzzzzzzzzzzz!!!!!!!!!

Answers
Answer:
1. a 2. d 3. c 4. d 5. b
Step-by-step explanation: