solve the equation by completing the square. 4x2 − x = 0 x = (smaller value) x = (larger value)
Answers
To solve the given equation, we need to complete the square. First, we can factor out 4 from the equation to get 4(x^2 - 1/4x) = 0. To complete the square, we need to add (1/2)^2 = 1/16 to both sides of the equation. This gives us 4(x^2 - 1/4x + 1/16) = 1. We can simplify this to (2x - 1/2)^2 = 1/4.
Taking the square root of both sides gives us 2x - 1/2 = ± 1/2. Solving for x, we get x = 1/4 or x = 0. Therefore, the smaller value of x is 0 and the larger value of x is 1/4. Completing the square helps us find the values of x that satisfy the equation by manipulating it into a form that can be more easily solved.
To solve the equation 4x² - x = 0 by completing the square, follow these steps:
1. Divide the equation by the coefficient of x² (4): x² - (1/4)x = 0
2. Take half of the coefficient of x and square it: (1/8)² = 1/64
3. Add and subtract the value obtained in step 2: x² - (1/4)x + 1/64 = 1/64
4. Rewrite the left side as a perfect square: (x - 1/8)² = 1/64
5. Take the square root of both sides: x - 1/8 = ±√(1/64)
6. Solve for x to find the two values: x = 1/8 ±√(1/64)
The smaller value: x = 1/8 - √(1/64)
The larger value: x = 1/8 + √(1/64)
To learn more about Equation: brainly.com/question/29657983
#SPJ11
Related Questions
what is the rate of change of y with respect of x for this solution

Answers
Answer:
5.2
Step-by-step explanation:
Solve for d.
-6 + d = 7 + 3d + 3
d = [
Submit
Answers
Answer:
so if add everything and subtract them for d you get 7
help plss and if u could plot the point as well thats better
TY

Answers
The linear functions defined in this problem are given as follows:
1. y = -x + 3.
2. y = x - 3.
3. y = 3x + 1.
4. y = -2x - 2.
How to define the linear functions?The slope-intercept definition of a linear function is given as follows:
y = mx + b.
The coefficients and their meaning are given as follows:
m is the slope, representing the rate of change of the output variable y relative to the input variable x.b is the y-intercept, representing the value of y when the graph of the function touches or crosses the y-axis.From the second bullet point above, the intercepts for each function in this problem are given as follows:
1. b = 3.2. b = -3.3. b = 1.4. b = -2.The slopes are given as follows:
1: m = -1, when x increases by 1, y decays by 1.2: m = 1, when x increases by 1, y increases by 1.3. m = 3, when x increases by 1, y increases by 3.4: m = -2, when x increases by 1, y decays by 2.Missing Information
The problem is incomplete, hence we just define the linear functions.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Now consider the so-called random walk with absorbing barriers on 1 = {0, 1, 2, 3, 4}. This is also a Markov chain on N = {0,1,2,3,4} with the following transition probability matrix P =
[1 0 0 0 0]
[1/2 0 1/2 0 0]
[0 1/2 0 1/2 0]
[0 0 1/2 0 1/2]
[0 0 0 0 1]
(a) Draw a graphical diagram that shows how this chain moves. (b) Is this chain irreducible? Why or why not? (c) Find E(X5 | X3 = 1, X0 = 2).
Answers
The random walk with absorbing barriers on the set {0, 1, 2, 3, 4} can be represented as a Markov chain with a transition probability matrix. This chain is irreducible since it is possible to reach any state from any other state. By evaluating the probabilities and the corresponding states, we can find the expected value E(X5 | X3 = 1, X0 = 2) for the given random walk with absorbing barriers.
(a) The graphical diagram representing the random walk with absorbing barriers on {0, 1, 2, 3, 4} can be visualized as a directed graph. Each state is represented by a node, and the arrows indicate the transition probabilities between states according to the given transition probability matrix P.
(b) The chain is irreducible because it is possible to reach any state from any other state. Starting from any state, there is always a positive probability of transitioning to any other state, including the absorbing states (0 and 4). This means that the chain does not have any disjoint subsets of states that are unreachable from one another.
(c) To find E(X5 | X3 = 1, X0 = 2), we condition on the starting state X0 = 2 and the state at time step 3, X3 = 1. Given this condition, we can calculate the expected value of X5, which represents the expected state at time step 5.
To compute this expectation, we can use the Markov property, which states that the future behavior of the chain depends only on its current state. Since X3 = 1 is known, we only need to consider the possible transitions from state 1 to other states according to the transition probability matrix P. By following these transitions, we can calculate the probability of reaching each state at time step 5 and then compute the expected value of X5 accordingly.
By evaluating the probabilities and the corresponding states, we can find the expected value E(X5 | X3 = 1, X0 = 2) for the given random walk with absorbing barriers.
To learn more about probability matrix click here: brainly.com/question/30974278
#SPJ11
if ∑an and ∑bn are both convergent series with positive terms, then ∑anbn is convergent.T/F
Answers
If the series ∑an and ∑bn are both convergent series with positive terms, then the series ∑anbn is also convergent.
This can be proven using the Comparison Test for series convergence. Since an and bn are both positive terms, we can compare the series ∑anbn with the series ∑an∑bn.
If ∑an and ∑bn are both convergent, then their respective partial sums are bounded. Let's denote the partial sums of ∑an as Sn and the partial sums of ∑bn as Tn.
Then, we have:
0 ≤ Sn ≤ M1 for all n (Sn is bounded)
0 ≤ Tn ≤ M2 for all n (Tn is bounded)
Now, let's consider the partial sums of the series ∑an∑bn:
Pn = a1(T1) + a2(T2) + ... + an(Tn)
Since each term of the series ∑anbn is positive, we can see that each term of Pn is the product of a positive term from ∑an and a positive term from ∑bn.
Using the properties of the partial sums, we have:
0 ≤ Pn ≤ (M1)(Tn) ≤ (M1)(M2)
Hence, if ∑an and ∑bn are both convergent series with positive terms, then ∑anbn is also convergent.
Therefore, the given statement is True.
learn more about convergent series here : brainly.com/question/32202517
#SPJ11
On a coordinate plane, a line goes through (0, negative 1) and (3, 1). a point is at (negative 3, 0). what is the equation of the line that is parallel to the given line and has an x-intercept of â€"3? y = two-thirdsx 3 y = two-thirdsx 2 y = negative three-halvesx 3 y = â€"three-halvesx 2
Answers
The equation of the line that is parallel to the given line and has an x-intercept of 3 is y = 2/3x - 2
What is the equation of the line that is parallel to the given line and has an x-intercept of 3?The given parameters are
Point =(0, -1) and (3, 1)
Calculate the slope using
m = (y₂ - y₁)/(x₂ - x₁)
Where m represents the slope
So, we have:
m = (1 -- 1)/(3 -0)
Evaluate
m = 2/3
Parallel lines have equal slopes
So, the slope of the other line is
m = 2/3
Linear equations are represented as:
y = mx + c
Where m represents the slope and c represents the y-intercept
So, we have
y = 2/3x + c
An x-intercept of 3 means
0 = 2/3 * 3 + c
So, we have
c = -2
Substitute c = -2 in y = 2/3x + c
y = 2/3x - 2
Hence, the equation of the line that is parallel to the given line and has an x-intercept of 3 is y = 2/3x - 2
Learn linear equations at
https://brainly.com/question/14323743
#SPJ4
Which situation could be represented by the graph
Answers
Answer:
what graph
Step-by-step explanation:
Zach substitutes the values 32 inches, 20 inches, and 20 inches into the Pythagorean theorem. Explain what Zach is most likely trying to find out.
Answers
Zach is trying to find out the hypotenuse value of the right-angle triangle.
What is the right triangle?
A right triangle is defined as a triangle in which one angle is a right angle or two sides are perpendicular.
The Pythagorean theorem states that "in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides".
Zach is most likely trying to find the length of the hypotenuse of a right triangle, which is the side opposite the right angle, given the lengths of the other two sides.
In this case, given 32 inches, 20 inches, and 20 inches values, he's trying to find out the hypotenuse value of the right-angle triangle.
Hence, Zach is trying to find out the hypotenuse value of the right-angle triangle.
To know more about right triangle, click on the link
https://brainly.com/question/2437195
#SPJ1
Which statements are true? Select three options
There are exactly two planes that contain points A,
B, and F
There is exactly one plane that contains points E, F,
and B
The line that can be drawn through points C and G
would lie in plane x,
The line that can be drawn through points E and F
would lie in planer
The only points that can lie on plane Yare points E
and F. my guy I literally have 5 days before graduation cmon man

Answers
Answer:
1. There is exactly one plane that contains points E,F, and B (2nd option)
2. The line that can be drawn through points C and G
would lie in plane x. (3rd option)
3. The line that can be drawn through points E and F
would lie in plane y. (4th option)
Step-by-step explanation:
The line that can be drawn through points C and G would lie in X-plane and the point E and F would lie in Y-plane. Then the correct options are C, D, and E.
What is a plane?A plane is a straight surface, with multiple surfaces that never end in maths.
The points C, D, and G lie in X-plane.
And the points E and F lie in Y-plane.
From the diagram, the conclusion points are given below.
The line that can be drawn through points C and G would lie in X-plane.The line that can be drawn through points E and F would lie in Y-planer.The only points that can lie on plane Y are points E and F.Then the correct options are C, D, and E.
More about the plane link is given below.
https://brainly.com/question/1962726
#SPJ5
Is the graph increasing, decreasing, or constant?
y
4
+
-8
4
8
8
-8
4
2.
-2
-2
A. Constant
B. Decreasing
C. Increasing
Answers
Geometry Math
Level : 9th Grade
Topic : Finding Angles with Justification
I have to find the angle
Example: ABC = 29 Degrees
**not true**
And the reasoning
Example :
SSA
SAS
AAS
And etc
The first person to give me all the answers will get marked and rewarded

Answers
Answer:
Step 3: The measure of angle DAB is 60°. Reason: Since DAE is a right angle, and EAB is 30 degrees, 90 - 30 is 60. (Just find the reason that is related to this statement).
Step 4: The measure of angle ABC is 130°. Reason: Same-side Interior Angles Theorem
Step-by-step explanation:
The polynomial 6x² + x - 15 has a factor of 2x - 3. What is the other factor?
3x - 5
O 3x + 5
O4x-5
O 4x + 5
Answers
Answer: Another factor is 3x + 5.
Step-by-step explanation:
please view the attachment for the steps.

The other factor of the polynomial (6x² + x - 15) would be (3x + 5). Hence option 2 is true.
Given that the polynomial is,
6x² + x - 15
And, The polynomial has a factor of 2x - 3.
Now apply the factorization method to solve for the factor,
6x² + x - 15
6x² + (10 - 9)x - 15
6x² + 10x - 9x - 15
2x (3x + 5) - 3 (3x + 5)
(2x - 3) (3x + 5)
Since The polynomial has a factor of 2x - 3.
Hence, the other factor would be (3x + 5). So option 2 is true.
To learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ5
aint the answer for this 10 just let me if im wrong

Answers
Answer:
Yup
Step-by-step explanation:
For the lucky ones
What is 2*2-45+2-4*37
25 points
Answers
Answer:
-187
Step-by-step explanation:
2*2-45+2-4*37
(multiply)
4-45+2-148
(calculate)
-187
Which value is greater 4/5 or 70%
Answers
Answer:
4/5
Step-by-step explanation:
4/5 = .8
70% = .7
Answer:
4/5
Step-by-step explanation:
If a ring costs $60 but the customer price is $90, what is the percent
increase?
Answers
Answer;
50% increase
Step-by-step explanation:
It would be 50% because 50% of 60 is 30 and 90 is 150% of 60, and so you're adding on 50%, or increasing 50%.
Find the length of the third side of the right triangle. Give an exact answer and an approximation to three decimal places if needed.

Answers
Answer:
a = 32
Step-by-step explanation:
This is a right triangle and the square value of hypotenuse is equal to sum of square value of other two side lengths
68^2 = 60^2 + a^2
4624 = 3600 + a^2
4624 - 3600 = a^2
1024 = a^2 find the root for both sides
32 = a
help, please Ill mark brainliest!

Answers
Answer:
the answers are 12.5, 5, 2, 0.8 and 0.32
Step-by-step explanation:
2(0.4)^-2
=2(6.25)
= 12.5
2(0.4)^-1
= 2(2.5)
=5
2(0.4)^0
=2(1)
=2
2(0.4)^1
=2(0.4)
=0.8
2(0.4)^2
=2(0.16)
=0.32
In a class , out of 40 students , 25 like maths only , 7 like science only , Slike both subjects . ( i ) Represent it in Venn - diagram . ( ii ) How many students do not like science ? ( ii ) How many students like science or maths ?
Answers
Answer:
STAY SAFE STAY UGLY.
Step-by-step explanation:
BY ELON MUSK
How does h(x) = -0.05x change over a unit interval in x?
Answers
Answer:
It changes downard 0.05 units
Step-by-step explanation:
We can easily see that h(x) is linear. That means it has a constant rate of change(i.e. the answer to the question is the same no matter the interval. It could be from 2 to 3, or 4 to 5, or -10000 to -9999, but the answer is the same).
Because the answer is the same across any interval, we can take the arbitrary interval 0 to 1 because it's easy to work with.
h(0)=-0.05(0)=0
h(1)=-0.05(1)=-0.05
As we can see, from 0 to 1, and thus for any unit interval, h(x) changes downard 0.05 units.
A study was conducted to compare the resting pulse rates (in beats per minute, BPM) of smokers to non-smokers. The difference in BPM was measured as smokers - nonsmokers. The 95% confidence interval of the difference in mean BPM was: -3.3 BPM < [u (smoke) – u (nonsmoke)] <10.9 BPM. < Based on this information, answer the following questions: 1. Did the smokers and non-smokers have significantly different mean BPMs? [ Select] 2. Who had the higher mean BPM in the sample? [ Select ] 3. If you had run the hypothesis test on this data, what would you have concluded? [Select ] 4. If you had run the hypothesis test on this data, what would your p-value have been? | [ Select]
Answers
A hypothesis is an informed prediction regarding the solution to a scientific topic that is supported by sound reasoning.
1. The 95% confidence interval for the difference in mean BPM between smokers and non-smokers based on the provided data is -3.3 BPM 10.9 BPM. The mean BPMs of smokers and non-smokers do not differ considerably, however this cannot be said with certainty because the confidence interval includes both positive and negative values.
2. It cannot be said with certainty whether group smokers or non-smokers had higher mean BPM based only on the confidence interval because it contains both positive and negative values. As a result, it is unclear whether the group's mean BPM was greater in the sample.
3. The null hypothesis can not be ruled out as per confidence interval, which contains both positive and negative numbers. According to null hypothesis, there is no discernible difference among smokers and non-smokers in terms of mean BPM. Thus, the conclusion will be that there is insufficient data to support the notion that smoking and non-smoking have significantly different mean BPMs.
4. If null hypothesis is correct, p-value indicates likelihood of receiving a result that is as extreme to or more extreme than the observed result. The precise value of p-value can not be identified since it is not included the given information. It would be necessary to determine the p-value using the proper statistical test, such as a t-test or a z-test, in order to determine if the observed difference is statistically significant.
Read more about hypothesis on:
https://brainly.com/question/26185548
#SPJ4
A bicycle has a listed price of $682.99 before tax. If the sales tax rate is 8.25%, find the total cost of the bicycle with sales tax
included.
Round your answer to the nearest cent, as necessary.
Answers
Answer:
739.34
Step-by-step explanation:
What is the 12th term in the sequence (1,3,5,7).
Answers
Answer:
23
Step-by-step explanation:
We Know
The sequence (1,3,5,7)
Each time it increases by 2
What is the 12th term in the sequence (1,3,5,7)?
Let's list it out
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23,....
So, the 12th term in the sequence is 23.
On a six-question multiple-choice test there are five possible answers for each question, of which one is correct (C) and four are incorrect (I). If a student guesses randomly and independently, find the probability of
a. Being correct only on questions 1 and 4 (i.e., scoring C, I, I, C, I, I).
b. Being correct on exactly two questions.
c. If X equals the number of correct answers in the six guesses, what is the p.m.f.; the mean; and the variance of X?
Answers
a. The probability of being correct only on questions 1 and 4 is (1/5) * (4/5) * (4/5) * (1/5) * (4/5) * (4/5) ≈ 0.01696. b. The probability of being correct on exactly two questions is 0.2304. c. The mean of X is 1.2 and the variance of X is 0.96.
a. To find the probability of being correct only on questions 1 and 4, we multiply the probabilities of getting a correct answer (C) on question 1, an incorrect answer (I) on questions 2 and 3, a correct answer on question 4, and incorrect answers on questions 5 and 6. The probability of getting a correct answer is 1/5, and the probability of getting an incorrect answer is 4/5. So the calculation becomes (1/5) * (4/5) * (4/5) * (1/5) * (4/5) * (4/5), which is approximately 0.01696.
b. To calculate the probability of being correct on exactly two questions, we can use the binomial distribution. The formula is P(X = k) = (n choose \(k) * p^k * (1-p)^(n-k),\)where n is the number of trials, k is the number of successes, and p is the probability of success in a single trial. In this case, n = 6, p = 1/5, and we want exactly 2 correct answers (k = 2). Plugging these values into the formula, we get P(X = 2) = (6 choose 2) * \((1/5)^2 * (4/5)^4,\)which is approximately 0.2304.
c. The probability mass function (p.m.f.) of X is a function that gives the probability of each possible number of correct answers in the six guesses. In this case, X can take values from 0 to 6. To calculate the p.m.f., we can use the binomial distribution formula for each value of X. The mean of X is calculated using the formula μ = n * p, where μ represents the mean, n is the number of trials, and p is the probability of success in a single trial. The variance of X is calculated using the formula \(σ^2 = n * p * (1-p),\) where \(σ^2\)represents the variance. For this problem, n = 6 and p = 1/5, so μ = 6 * (1/5) = 1.2 and\(σ^2\) = 6 * (1/5) * (4/5) = 0.96.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A water tank currently contains 275 gallons of water. The amount of water in the tank will decrease at a constant rate of 15 gallons per week. Which functions can be used to find t, the total number of gallons of water in the tank after w weeks.

Answers
The total number of gallons of water in the tank after w weeks is 275 - 15w.
What is a function?
Each element of X receives exactly one element of Y when a function from one set to the other is used. The sets X and Y are collectively referred to as the function's domain and codomain, respectively. Initially, functions represented the idealized relationship between two changing quantities.
Here, we have
Given: A water tank currently contains 275 gallons of water. The amount of water in the tank will decrease at a constant rate of 15 gallons per week.
To determine the function that can be used to evaluate 't', the total number of gallons of water in the tank after w weeks:
Let the total number of weeks be 'w'.
So, the total amount of water reduced from the tank is:
= 15w
The functions that can be used to evaluate 't', the total number of gallons of water in the tank after w weeks are given below:
G(t) = 275 - 15w
Hence, the total number of gallons of water in the tank after w weeks is 275 - 15w.
To learn more about the function from the given link
https://brainly.com/question/10439235
#SPJ1
A. y=-2x+6
B. y=2x +6
C. y= -1/2x +6
D. y=1/2x+6
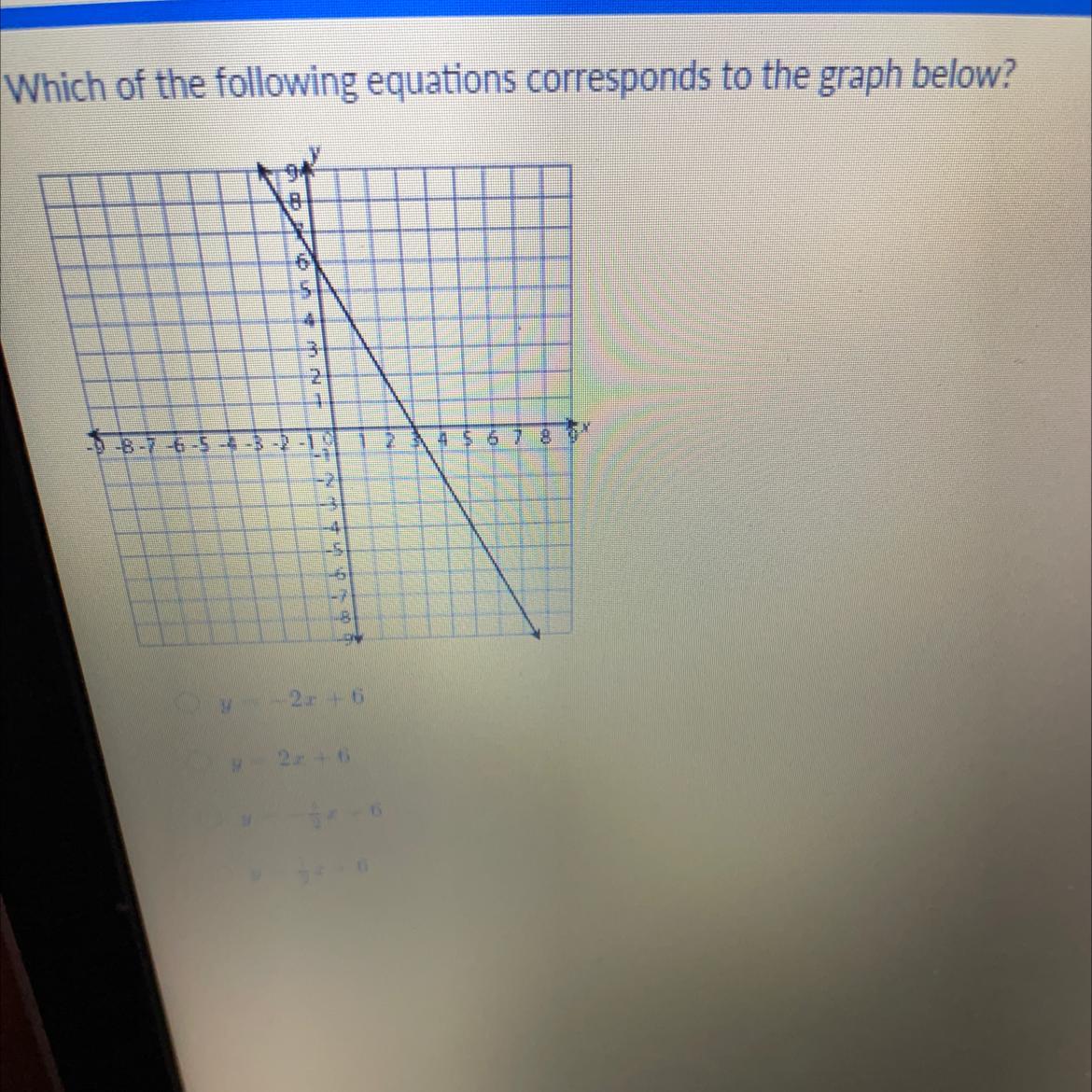
Answers
Answer:
A. y=-2x+6
Step-by-step explanation:
without using symmetry, determine a definite integral that represents the area of the region enclosed by r = 1 sin θ .
Answers
The definite integral that represents the area of the region enclosed by the polar curve r = 1 sin θ is ∫[a, b] 1/2 r^2 dθ
To determine the definite integral that represents the area of the region, we integrate the expression 1/2 r^2 with respect to θ over the interval [a, b], where a and b are the limits of the region.
In this case, the polar curve r = 1 sin θ represents a circle with radius 1 centered at the origin. As θ varies from 0 to π, the curve traces half of the circle in the positive direction. To find the area of the region enclosed by this curve, we integrate the expression 1/2 r^2 over this interval.
The expression 1/2 r^2 represents the area of a sector of the circle with radius r and central angle θ. Integrating this expression with respect to θ gives us the total area enclosed by the curve.
By evaluating the definite integral over the interval [a, b], we can find the area of the region enclosed by the polar curve r = 1 sin θ.
To know more about area click here
brainly.com/question/13194650
#SPJ11
Do the following side lengths form a right triangle?
95, 76, 57
Answers
Answer:
Yes
Step-by-step explanation:
A right triangle is a triangle that has one angle whose measure is 90°. A right triangle CANNOT have two 90º angles. This is because the angles of a triangle must add up to 180°. With one angle measuring 90°, the other two angles in the right triangle must add up to 90°
If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has:_________
Answers
If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has exactly one solution.
This is because the linear function intersects the quadratic function at its minimum point, where there is only one value of x that satisfies both equations.
If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has one unique solution.
Here's a step-by-step explanation:
1. A nonlinear system is a set of equations where at least one of the equations is not linear.
2. In this case, the nonlinear system contains one linear function and one quadratic function.
3. The quadratic function has a minimum point, which is the lowest point of its parabolic graph.
4. The linear function touches the quadratic function at its minimum, which means they intersect at exactly that point.
5. Since the two functions intersect at one point, the system has one unique solution, which corresponds to the coordinates of that intersection point.
Visit here to learn more about quadratic function:
brainly.com/question/30929439
#SPJ11
Let 0≤s≤r≤k≤n. Give a combinatorial proof of the following identity. ( n
k
)( k
r
)( r
s
)=( n
s
)( n−s
r−s
)( n−r
k−r
) [Hint: count the number of triples (A,B,C) such that A⊆B⊆C⊆T, where ∣A∣=s,∣B∣=r,∣C∣=k and ∣T∣=n in two different ways.] Note: you may attempt an algebraic proof for reduced credit of most 12/20 points
Answers
The combinatorial proof of the given identity can be demonstrated by counting the number of triples (A, B, C) such that A⊆B⊆C⊆T, where |A|=s, |B|=r, |C|=k, and |T|=n.
First, let's consider counting the triples by fixing the sizes of the sets. We choose s elements for set A out of n, then r elements for set B out of the remaining n-s elements, and finally, k elements for set C out of the remaining n-r elements. This can be represented as (n choose s)(n-s choose r)(n-r choose k).
On the other hand, we can count the triples by fixing the contained relationship. We choose a set C of size k out of n elements. Then, we select a subset A of size s from the k elements in C. Finally, we choose a subset B of size r from the k elements in C, which may or may not contain the elements of A. This can be represented as (n choose k)(k choose s)(k choose r).
Since both counting methods represent the same set of triples, they must be equal. Therefore, we have:
(n choose s)(n-s choose r)(n-r choose k) = (n choose k)(k choose s)(k choose r)
This provides a combinatorial proof of the given identity.
Learn more about combinatorial proof from the given link:
https://brainly.com/question/32759019
#SPJ11