Answers
By constructing and solving the profit equation for the cuckoo clock sales, we conclude that the sales of 30 clock will make a profit of $ 4250
How to determine the monthly profit by the cuckoo clock sales
The profit (P) is the result of subtracting costs from sales (S). Cost (Cp) is the sum of rent (C) and production cost (C'). Now we proceed to create and solve the expression:
P = S - C - C'
P = 500 · x - 275 · x - 2500
P = 225 · x - 2500
P = 225 · 30 - 2500
P = 4250
By constructing and solving the profit equation for the cuckoo clock sales, we conclude that the sales of 30 clock will make a profit of $ 4250.
To learn more on profits: https://brainly.com/question/13716014
#SPJ1
Related Questions
The ratio of adult cats to kittens at a pet care center on Wednesday was 5.3 there where 27 kittens there that day.monday 48 adult cats where at the pet care center.what is the difference between the number of adult cats at the pet care center on Monday and Wednesday
Answers
The difference between the number of adults cats at the pet centre on Monday and Wednesday is 3.
What is ratio?Ratio, in math, is a term that is used to compare two or more numbers.
The ratio of adult cats to kittens at a pet care centre on Wednesday was 5:3. There were 27 kittens there that day.
Hence, let
total number of cat on Wednesday = x
Hence,
27 = 3 / 8 x
cross multiply
3x = 216
x = 216 / 3
x = 72
Hence,
adult cat on Wednesday = 72 - 27 = 45
The difference between the number of adult cats at the pet centre on Monday and Wednesday can be computed as follows:
difference = 48 - 45 = 3
learn more on ratio here:https://brainly.com/question/18455434WHat
#SPJ1
Consider the two functions below. Which one of these functions is linear? What is its equation? Enter any answers to two decimal places

Answers
Answer:
A
Step-by-step explanation:
A linear function is a straight line when graphed so is not B.
For confirmation of A note how for each increase of 3 in x we get the same increase of 5 in y.
Solve the system. It there is no solution or it there are infinitely many solutions and the system's equations are dependent, so state. 2x+y=−1 x+y−z=−4 3x+3y+z=0 Select the correct choice below and fill in any answer boxes within your choice. A. There is one solution. The solution set is {()}. (Simplify your answers.) B. There are infinitely many solutions. C. There is no solution.
Answers
The given system of equations has infinitely many solutions.
Explanation:
To determine the number of solutions for the given system of equations, we can analyze the system using various methods such as substitution, elimination, or matrix operations. Let's use the method of elimination to solve the system.
Given equations:
1) 2x + y = -1
2) x + y - z = -4
3) 3x + 3y + z = 0
We can start by manipulating the equations to eliminate variables. Multiplying equation 2 by 2 and adding it to equation 1 will cancel out the variable "y":
1) 2x + y = -1
2) 2(x + y - z) = 2(-4) -> 2x + 2y - 2z = -8
Adding equation 1 and the modified equation 2 gives us:
4x - 2z = -9 (equation 4)
Next, let's multiply equation 3 by -2 and add it to equation 4 to eliminate the variable "z":
-6x - 6y - 2z = 0
4x - 2z = -9
Simplifying:
-6x - 6y - 2z + 4x - 2z = 0 - 9
-2x - 6y - 4z = -9
Dividing the equation by -2:
x + 3y + 2z = 4.5 (equation 5)
Now we have equations 4 and 5:
4x - 2z = -9
x + 3y + 2z = 4.5
Looking at the equations, we notice that the variable "x" can be eliminated by multiplying equation 5 by 4 and adding it to equation 4:
4(x + 3y + 2z) = 4(4.5) -> 4x + 12y + 8z = 18
Adding equation 4 and the modified equation 5 gives us:
4x - 2z + 4x + 12y + 8z = -9 + 18 (equation 6)
Simplifying:
8x + 12y + 6z = 9 (equation 6)
From equations 6 and 5, we can see that both have the same coefficients for variables "x," "y," and "z." This indicates that the two equations are dependent and represent the same line in three-dimensional space.
Since the system has dependent equations, there are infinitely many solutions. In other words, any values of "x," "y," and "z" that satisfy the equation of the line represented by the system will be a solution.
Learn more about system of equations
brainly.com/question/21620502
#SPJ11.
find the area of this triangle

Answers
Work Shown:
area = 0.5*base*height
area = 0.5*11*13.4
area = 73.7 square cm
The other values 15 and 14 are not used. Your teacher probably put them in as a distraction.
Jaime wrote 4.4-0.33=1.1 .Is his answer reasonable why or why not?
Answers
Answer: No it would be 4.07
=1.1
Step-by-step explanation: Subtract 0.33 from 4.4
Q1. Convert the following LPs to standard form: minz=3x1+x2 s.t.
x1>=3
x1+x2<=4
2x1−x2=3
x1,x2>=0
minz=3x1+x2
s.t.
x1>=3
x1+x2<=4
2x1−x2=3
x2>=0,x1: unrestricted
Answers
The standard form of the LP is
min z = 3x1 + x2
s.t.
x1+ - 3 >= 0
x2 >= 0
x2 <= 4 - x1
2x1 - x2 + s = 3
x1+, x1, x2, s >= 0.
The problem is in standard form with all constraints as "≤" inequalities and all variables non-negative.
To convert the given linear programming problem (LP) into standard form, we need to make sure that all the constraints are of the form "≤" and the objective function is in the form of "minimize" or "maximize" with all variables on the right side.
1. Start by converting the objective function. The given objective function is already in the form of "minimize," so no changes are needed.
2. Next, convert the first constraint, x1 >= 3. Since it is already in the correct form, we can move on to the second constraint.
3. Convert the second constraint, x1 + x2 <= 4. To convert it to the "≤" form, subtract x1 from both sides: x2 <= 4 - x1.
4. Now, convert the third constraint, 2x1 - x2 = 3.
Since it is an equation, we need to introduce a slack variable to convert it into an inequality.
Add a new variable, s, and rewrite the constraint as follows: 2x1 - x2 + s = 3.
5. Finally, we need to ensure that all variables are non-negative.
The given constraint x2 >= 0 is already in the correct form, but x1 has no explicit lower bound.
To address this, we can introduce a new variable, x1+, and rewrite x1 as the difference between x1+ and 3: x1 = x1+ - 3.
The standard form of the LP is now:
min z = 3x1 + x2
s.t.
x1+ - 3 >= 0
x2 >= 0
x2 <= 4 - x1
2x1 - x2 + s = 3
x1+, x1, x2, s >= 0.
In summary, the LP is converted to standard form by rewriting the constraints and introducing additional variables as necessary to ensure all constraints are in the form of "≤" and the objective function is in the form of "minimize."
Learn more about slack variable, here
https://brainly.com/question/33373374
#SPJ11
w(n)=n^2-3
Find w(-3)
Answers
Answer:
6
Step-by-step explanation:
w(-3)=-3^2-3
w(-3)=9-3 = 6
Answer:
w(-3)=6
Step-by-step explanation:
w(n)=n^2-3
w(-3)=-3^2-3
w(-3)=9-3
6
Fist you change the n to -3.
Next you multiply -3 times -3 and two negatives multipled together makes a positve so it would be 9.
Then you subtract 9 and 3 and yo get six.
P.S. if you have a number, for example 5, then there is a ^2 above the five, which means you multiply 5 by 5.
suppose you drive an old truck with a 32 gallon gas tank that gets 16 miles/gallon. if you are 75 miles from home and you have a quarter tank of gas, will you run out of gas before you get home?
Answers
The answer is no, the truck will not run out of gas before getting home.
To solve the problem, the following terms are needed:
32 gallons = Capacity of the gas tank
16 miles/gallon = The truck's fuel economy
75 miles = The distance from home to the truck
Quarter tank = The remaining fuel level
The capacity of the gas tank is 32 gallons.
Since a quarter of the tank is remaining, the amount of fuel in the tank is \(32/4 = 8 gallons\).
A truck with a fuel efficiency of 16 miles per gallon is capable of driving for 8 gallons x 16 miles per gallon \(= < < 8*16\)
\(=128 > > 128\) miles on the remaining fuel level.
The remaining distance is 75 miles, so the truck will not run out of gas before reaching home since 75 miles is less than 128 miles that the truck can drive with the remaining fuel in the tank.
Therefore, the answer is no, the truck will not run out of gas before getting home.
Know more about distance here:
https://brainly.com/question/26550516
#SPJ11
Solution:
20. RAINFALL The amount of rainfall on Monday
and Thursday is shown in the table. If the same
amount of rain that fell on Monday fell for 3 days
and the same amount that fell on Thursday fell for
2 days, how much rain would fall over those 5
days?
Day
Rain (in.)
Equation:
Monday
0.50
Thursday
0.25
Answers
Here is how to solve it :
0.50 x 3 = 1.5
0.25 x 2 = 0.5
1.5 + 0.5 = 2
Determine the quotient of
3/7 divided by 2/3
Answers
Okay, so dividing fractions is the same thing as multiplying by the reciprocal. Which means 2/3 will be flipped over to 3/2 now multiplying 3/7 x 3/2 you will get 9/14
Between which two integers does square root of /10
lie?
Answers
Answer:
It is lie
Step-by-step explanation:
Fdfdddddhfhdhdhdhdhhdhdhdhd
Answer:
Between 3 and 4.
Step-by-step explanation:
Due to the square root of 10 being around 3.16, the value is between 3 and 4.
However, we can also find this by saying the closest two integers to the square root of 10 are 3 and 4 due to 3^3 = 9 and 4^2 = 16 and 10 being between those two values.
Hope this helped!
Yaritza is driving on a long road trip. she currently has 13 gallons of gas in her car. each hour that she drives, her car uses up 0.75 gallons of gas. how much gas would be in the tank after driving for 5 hours? how much gas would be left after t hours?
Answers
Answer:
9.25
13 - 0.75t
Step-by-step explanation:
0.75 * 5 = 3.75
13 - 3.75 = 9.25
hope this helps!
Help please ........

Answers
Answer:
D
Step-by-step explanation:
eh too lazy to explain but plz trust me
An item is regularly priced at $35. It is now priced at a discount of 40% off the regular price. What is the price now?
Answers
Answer:
15
Step-by-step explanation:
4. A ship is travelling at a heading of \( 220^{\circ} \) at a speed of 14 knots. A current is flowing at a speed of knots, at a bearing of \( 060^{\circ} \). What is the ship's ground speed?
Answers
\(Given, Heading of the ship is \(220^{\circ}\) and the Speed of the ship is 14 knots current is flowing at a speed of knots, at a bearing of \(060^{\circ}\)Let the speed of current be x knots.\)
The ship's ground speed is the vector sum of the velocity of the ship and the velocity of the current.
Ground speed of the ship = The resultant velocity of the ship and velocity of current ground speed of the ship = \(√((Ship's speed)² + (Speed of current)² + 2 (Ship's speed) (Speed of current) cos θ)θ\) is the angle between the velocity vector of ship and the velocity vector of current ground speed of ship = \(√((14)² + x² + 2(14) (x) cos (220° - 60°))\)
\(We know, cos (220° - 60°) = cos 160° = -1/2
By putting this value,\)
\(Ground speed of ship = √((14)² + x² + 2(14) (x) (-1/2))\)
\(Ground speed of ship = √(196 + x² - 14x)
Hence, the ship's ground speed is √(196 + x² - 14x) .\)
To know more about the word velocity visits :
https://brainly.com/question/22038177
#SPJ11
To find the ship's ground speed, we need to consider the effect of both the ship's heading and the current's direction and speed.
Let's break down the given information:
Ship's heading: \(\(220^\circ\)\) (measured clockwise from north)
Ship's speed: 14 knots
Current's direction: \(\(060^\circ\)\) (measured clockwise from north)
Current's speed: unknown (let's call it (C) knots)
To find the ship's ground speed, we can use vector addition. The ship's velocity vector (ship's speed and direction) and the current's velocity vector (current's speed and direction) will combine to give us the resultant velocity vector (ground speed and direction).
To solve this, we can use the law of cosines to find the magnitude of the resultant velocity vector.
The law of cosines states:
c^2 = a^2 + b^2 - 2ab * cos(C)
Where:
c = magnitude of the resultant velocity vector (ground speed)
a = magnitude of the ship's velocity vector (ship's speed)
b = magnitude of the current's velocity vector (current's speed)
C = angle between the ship's velocity vector and the current's velocity vector
In this case, the angle C is the difference between the ship's heading and the current's direction:
C = (ship's heading) - (current's direction)
C = 220° - 60°
C = 160°
Plugging in the known values into the law of cosines equation:
c^2 = (14)^2 + (C)^2 - 2(14)(C) * cos(160°)
Now, we need to find the value of C (current's speed) in order to solve for c (ground speed).
Unfortunately, the current's speed (C) is not provided in the given information. Please provide the value of the current's speed (in knots), and I will be able to calculate the ship's ground speed.
To know more about speed visit:
https://brainly.com/question/17661499
#SPJ11
En un quiosco hay 40 cajas de cromos. Cada caja contiene 25 paquetes. Cada paquete lleva 7 cromos. El quiosquero vende 12 paquetes. ¿Cuantos cromos quedan en el quiosco? Escribe todos los calculos en una sola expresion
Answers
Las ecuaciones algebraicas son ecuaciones que contienen variables desconocidas. Estas variables desconocidas se pueden representar con cualquier letra del alfabeto.
Por lo tanto, quedan 6916 pegatinas en el quiosco.
Paso 1: En un quiosco, hay 40 cajas de pegatinas. Cada caja contiene 25 paquetes.Por lo tanto, el número total de paquetes en 40 cajas de pegatinas es:
1 caja = 25 paquetes
40 cajas =?
Multiplicar cruzada
40 cajas × 25 paquetes / 1 caja
= 1000 paquetes.
Hay 1000 paquetes de pegatinas en 40 cajas.
Paso 2: cada paquete tiene 7 pegatinas.1 paquete = 7 pegatinas
1000 paquetes =?
Multiplicar cruzada
1000 paquetes × 7 pegatinas / 1 paquete
= 7000 pegatinas
Hay 7000 pegatinas en 40 cajas.
Paso 3: el quiosco vende 12 paquetes. ¿Cuántas pegatinas quedan en el quiosco?El número total de paquetes = 1000 paquetes
El número de paquetes que quedan después de vender 12 paquetes es
1000 - 12
= 988 paquetes
Quedan 988 paquetes.
Paso 4: conversión de la cantidad de paquetes que quedan en pegatinas1 paquete = 7 pegatinas
988 paquetes =?
Multiplicar cruzada
988 paquetes × 7 pegatinas / 1 paquete
= 6916 pegatinas
Por lo tanto, quedan 6916 pegatinas en el quiosco.
Para obtener más información, visite el enlace a continuación:
brainly.com/question/20964056
Two friends shop for fresh fruit. elena buys a watermelon for $7.65 and 4 pounds of cherries. taniy buys a pineapple for $2.25 and 3 pounds of cherries. use the variable p to represent the price, in dollars, per pound of cherries.
Answers
Answer:Answer: 5.2-p
Step-by-step explanation:
Let p be the price, in dollars, per pound of cherries.
Given : .Jackson buys a watermelon for $7.65 and 5 pounds of cherries.
Cost of 5 pounds of cherries = 5p
Now,
Cost of fruits to Jackson = 7.65+5p (in dollars)
Tim buys a pineapple for $2.45 and 4 pounds of cherries.
Cost of 4 pounds of cherries = 4p
Now,
Cost of fruits to Tim = 2.45+4p (in dollars)
Amount spent by Jackson more than Tim = (Cost of fruits to Jackson)-(Cost of fruits to Tim)
= 7.65+5p -(2.45+4p)
= 7.65+5p -2.45 - 4p
= 5.2-p
Hence , the required expression in terms of p = "5.2-p"
Step-by-step explanation:
will somebody please help

Answers
Answer:
Step-by-step explanation:
it should be 34
Answer:
x° = 34°.Step-by-step explanation:
Given equation:
90 - 56We are finding the value of x.
Solve:
90 - 56= 34.x° = 34°.
a stone is dropped from the top of a cliff. it is observed to hit the ground 5.78 s later how high is the cliff?
Answers
Using the formula;
H= ut + 1/2 gt²
The initial velocity = 0
Hence H= 1/2 gt²
g= 10m/s t= 5.78 s
H = 1/2 x 10 x 5.78²
H = 167.042 m
H = 167 m approximately
a) Set-up an integral for the area of the surface obtained by rotating the curve y=tanx,0≤x≤π3about the x-axisb) Set-up an integral for the area of the surface obtained by rotating the curve y=tanx,0≤x≤π3about the y-axis
Answers
The area of the surface obtained by the curve rotated along the x-axis is \(S_1=\int\limits_0^{\pi/3}2\pi (\tan x)\sqrt{1+\sec^4x}\;dx\). The area of the surface obtained by the curve rotated along the y-axis is \(S_2=\int\limits_0^{\sqrt{3}}2\pi (\tan^{-1}y)\sqrt{1+\left(\frac{1}{1+y^2}\right)^2}\;dy\).
A surface type that results from rotating a curve around a specific axis is the area of the surface of revolution. The formula for the area around the x-axis is given by, \(S_1=\int\limits_a^b2\pi f(x)\sqrt{1+(f'(x))^2}\;dx\) and around the y-axis is \(S_2=\int\limits_a^b2\pi g(y)\sqrt{1+(g'(y))^2}\;dy\).
a) Given the expression is rotated about the x-axis. Let,
\(\begin{aligned}f(x)&=y\\&=\tan x \in \left[0,\frac{\pi}{3}\right] \end{aligned}\)
Then,
\(f'(x)=\sec^2x.\)
Substitute f(x) and f'(x) value in the S₁ formula, we get,
\(S_1=\int\limits_0^{\pi/3}2\pi (\tan x)\sqrt{1+\sec^4x}\;dx\)
b) Given the expression is rotated about the y-axis. Let,
\(\begin{aligned}x&=g(y)\\&=\tan^{-1}y \in \left[0, \sqrt{3}\right] \end{aligned}\)
Then,
\(g'(y)=\frac{1}{(1+y^2)}\)
Substitute g(y) and g'(y) value in the S₂ formula,
\(S_2=\int\limits_0^{\sqrt{3}}2\pi (\tan^{-1}y)\sqrt{1+\left(\frac{1}{1+y^2}\right)^2}\;dy\)
To know more about the area of a surface of revolution:
https://brainly.com/question/29992924
#SPJ4
The complete question is -
a) Set up an integral for the area of the surface obtained by rotating the curve y=tanx,0≤x≤π/3 about the x-axis.
b) Set up an integral for the area of the surface obtained by rotating the curve y=tanx,0≤x≤π/3 about the y-axis.
For the in parts A through E, choose the highest level of measurement (or cannot be determine).
A. Temperature of refrigerators ---
Nominal
Ratio
Cannot determine
Interval
Ordinal
B. Horsepower of race car engines ---
Ordinal
Interval
Nominal
Cannot determine
Ratio
C. Marital status of school board members ---
Interval
Nominal
Ordinal
Cannot determine
Ratio
D. Ratings of televisions programs (poor, fair, good, excellent) ---
Ordinal
nominal
Interval
Cannot determine
Ratio
E. Ages of children enrolled in a daycare
Ordinal
nominal
Interval
Cannot determine
Ratio
Answers
Temperature of refrigerators - Cannot determine. Horsepower of race car engines - Ratio. Marital status of school board members - Nominal. Ratings of television programs - Ordinal. Ages of children enrolled in a daycare - Interval
The level of measurement for the temperature of refrigerators cannot be determined based on the given information. The temperature could potentially be measured on a nominal scale if the refrigerators were categorized into different temperature ranges. However, without further context, it is not possible to determine the specific level of measurement.
The horsepower of race car engines can be measured on a ratio scale. Ratio scales have a meaningful zero point and allow for meaningful comparisons of values, such as determining that one engine has twice the horsepower of another.
The marital status of school board members can be measured on a nominal scale. Nominal scales are used for categorical data without any inherent order or ranking. Marital status categories, such as "married," "single," "divorced," etc., can be assigned to school board members.
The ratings of television programs, such as "poor," "fair," "good," and "excellent," can be measured on an ordinal scale. Ordinal scales represent data with ordered categories or ranks, but the differences between categories may not be equal or measurable.
The ages of children enrolled in a daycare can be measured on an interval scale. Interval scales have equal intervals between values, allowing for meaningful differences and comparisons. Age, measured in years or months, can be represented on an interval scale.
Learn more about nominal scale visit:
brainly.com/question/28465126
#SPJ11
if z is a standard normal variable, find the probability that z lies between −2.41 and 0. round to four decimal places.
Answers
The probability that z lies between -2.41 and 0 is approximately 0.9911.
What is the probability of z falling within a specific range?To find the probability that a standard normal variable, z, falls within a specific range, we can use the standard normal distribution table or a statistical calculator.
In this case, we want to find the probability that z lies between -2.41 and 0. By referencing the standard normal distribution table or using a calculator, we can determine the area under the curve corresponding to this range. The resulting value represents the probability of z falling within that range.
Approximately 0.9911 is the probability that z lies between -2.41 and 0 when rounded to four decimal places. This means that there is a high likelihood (approximately 99.11%) that a randomly chosen value of z from a standard normal distribution falls within this range.
Learn more about probability
brainly.com/question/31828911
#SPJ11
Work out the length of x.
Give your answer rounded to 3 significant figures.
8.6 cm+
x
The diagram is not drawn accurately.
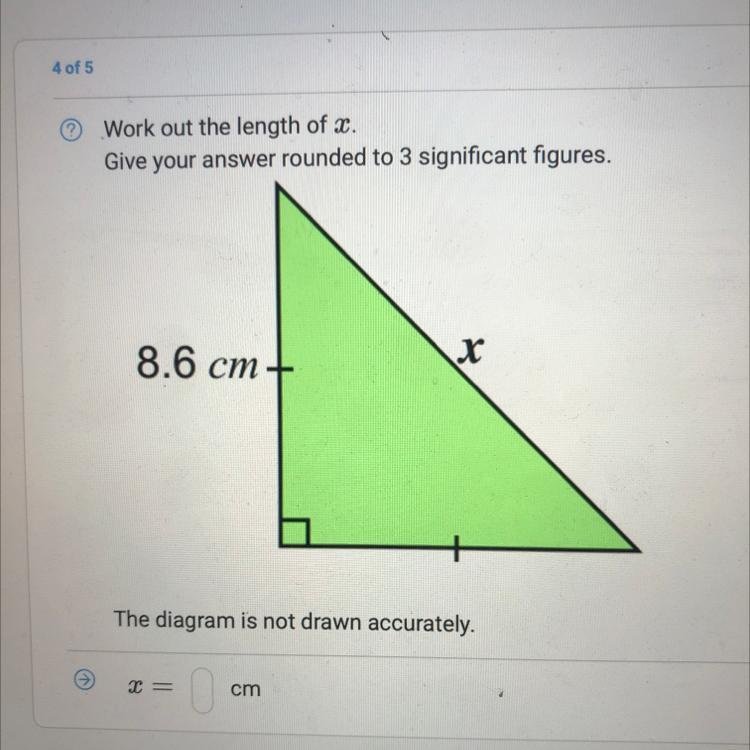
Answers
Answer:
12.2cm
Step-by-step explanation:
Follow the steps in the image I send you to learn it if you don't get it tell me.


a line has a slope of -3, so it's equation has the form y= -3x + b. the line passes through the point (1, -2). what is the y-intercept, b, of the line?
Answers
Answer:
y-intercept = 1
Step-by-step explanation:
y = -3x + b
(1 , -2)
Plugin the equation
-2 = -3*1 + b
-2 = -3 + b
-2 + 3 = b
1 = b
What is the percent of change from 72 to 36?
Answers
The answer should be negative 50
4 over 5 ÷ 1 over 10 =
Answers
Answer:
8
Step-by-step explanation:
Factor the numerator and denominator and cancel the common factors.
The standard error of the estimate is
A.the amount of error that is calculated amongst variables
B.the same amount of error throughout, hence being standard
C. the measure of variability around the line of regression
D. the measure of the volatility of the independent variable
Answers
the standard error of the estimate provides a measure of the variability around the regression line, helping us understand how well the line predicts the dependent variable based on the independent variable(s).The correct answer is C.
The standard error of the estimate is the measure of variability around the line of regression. It quantifies how accurately the regression line predicts the dependent variable based on the independent variable(s).
To understand this concept, let's consider an example. Suppose we have a dataset of students' test scores and the amount of time they spent studying. We want to use linear regression to predict test scores based on study time. The regression line represents the best-fit line that minimizes the overall distance between the predicted and actual test scores.
The standard error of the estimate tells us how much the actual test scores vary from the predicted scores. A lower standard error indicates that the regression line is a better fit to the data, meaning the predictions are more accurate. Conversely, a higher standard error indicates more variability and less accuracy in the predictions.In summary, the standard error of the estimate provides a measure of the variability around the regression line, helping us understand how well the line predicts the dependent variable based on the independent variable(s).
Learn more about Regression here,https://brainly.com/question/28178214
#SPJ11
determine the general solution of 6 sin squared x + 7 cos x - 3 is equals to zero
Answers
Step-by-step explanation:
To solve the equation:
6(sin(x))^2 + 7cos(x) - 3 = 0
We can use the identity:
sin^2(x) + cos^2(x) = 1
Rearranging the equation, we get:
6(1-cos^2(x)) + 7cos(x) - 3 = 0
Expanding and rearranging, we get:
6cos^2(x) + 7cos(x) - 9 = 0
This is now a quadratic equation in terms of cos(x).
Using the quadratic formula, we get:
cos(x) = [-7 ± √(7^2 - 4(6)(-9))]/(2(6))
cos(x) = [-7 ± 13]/12
cos(x) = 1/2 or -3/2
Now we use the inverse cosine function to find x for each solution for cos(x).
When cos(x) = 1/2, we get:
x = π/3 + 2πk or x = 5π/3 + 2πk
When cos(x) = -3/2, we get:
there are no solutions for this case.
Therefore, the general solution to the equation is:
x = π/3 + 2πk or x = 5π/3 + 2πk where k is an integer.
Suppose that 17 inches of wire costs 51 cents.
At the same rate, how much (in cents) will 13 inches of wire cost?
Answers
Answer:
$0.39
Step-by-step explanation:
51/17 = 3
$0.03 per inch
0.03 × 13 = 0.39
$0.39
Troy needs to complete 45 hours of training. During the fall, Troy completed 12 hours of training, and during the spring he completed twice as many hours as he had during the fall. Which equation can be used to find how many more hours of training (h) Troy needs to complete? Select one:
Answers
Answer:
\(36 + h = 45\)
\(h = 9\)
Step-by-step explanation:
Given
\(Total = 45\)
\(Fall = 12\)
\(Spring = 2 * Fall\)
Required
Determine the equation to find the hours (h) left
The sum of the hours spent during the fall, spring and the hours left must be equal to the total hours.
In other word;
\(Fall + Spring + h = Total\)
Substitute 2 * Fall for Spring
\(Fall + 2 * Fall + h =Total\)
Substitute values for Fall and Total
\(12 + 2 * 12 + h = 45\)
\(12 + 24 + h = 45\)
\(36 + h = 45\)
The above represents the equation,
Solving further for h
\(h = 45 - 36\)
\(h = 9\)
Hence, there are 9 hours left
