Point u is on line segment tv given tv = x + 10, tu =3x-8, and Uv = 10 determine the numerical length of tv
Answers
Answer:
\(|tv = 14\)
Step-by-step explanation:
Given
\(|tv = x + 10\)
\(|tu = 3x - 8\)
\(|uv = 10\)
Required
Determine length of tv
Length tv is calculated by adding lengths tu and uv.
In other words
\(tv = tu + uv\)
Substitute values for tv, tu and uv
\(x + 10 = 3x-8+10\)
Collect like terms
\(x - 3x = -8+10 -10\)
\(-2x = -8\)
Divide both sides by -2
\(x = 4\)
Recall that \(|tv = x + 10\)
Substitute 4 for x
\(|tv = 4 + 10\)
\(|tv = 14\)
Hence, the length of line segment tv is 14
Related Questions
Given that A={1,2,3,4,5} list the elements of the following sets. i.{x2:x€A} ii.{ :x€A} iii.{2x :x€A} iv.{4x+1:x€A}
Answers
Answer:no idea
Step-by-step explanation:
Please help me I’ll mark you brainly

Answers
On solving the provided question, we can say that - here in graph we have on solving equation \(2x^2+ 9y^2 \\\) = \(8 + 9 = 17\)
What is equation?An equation is a formula in mathematics that joins two statements with the equal symbol = to represent equality. The definition of an equation in algebra is a mathematical statement proving the equality of two mathematical expressions. In the equation 3x + 5 = 14, for instance, the terms 3x + 5 and 14 are separated by an equal sign. The link between two phrases on either side of a letter is expressed mathematically. There is often only one variable, which is also the symbol. instance: 2x - 4 Equals 2.
here,
from graph, x= 2
y = 1
\(2x^2+ 9y^2 \\\)
\(8 + 9 = 17\)
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Use the diagram below to find the measure of CAD.
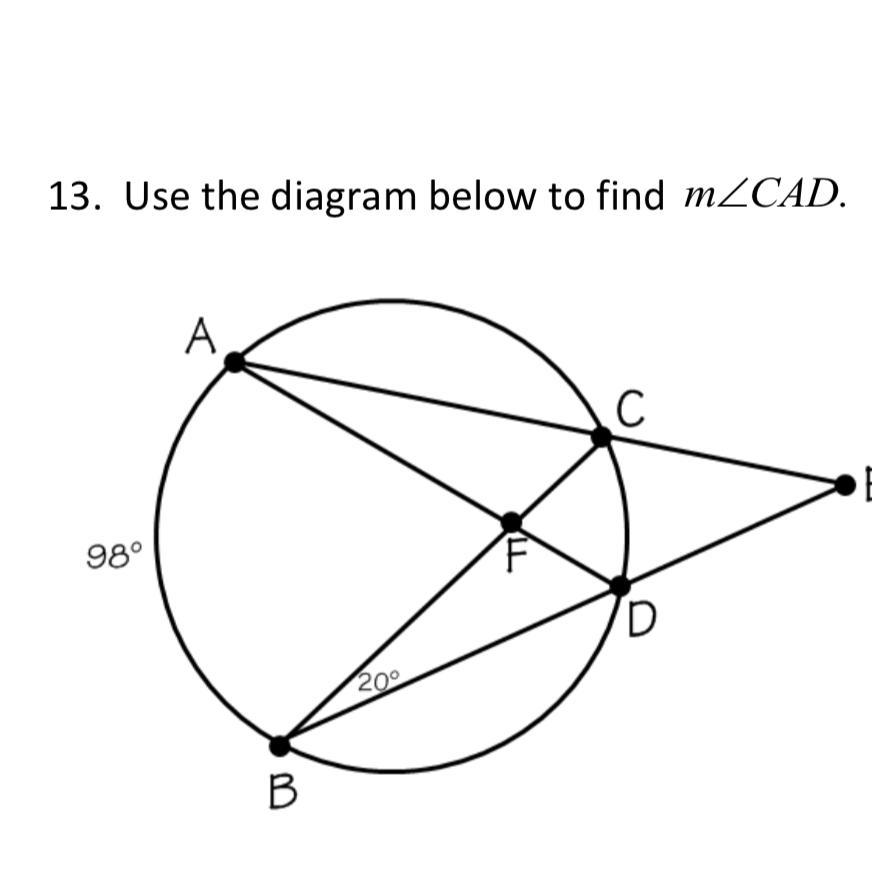
Answers
Answer:
\(\angle CAD = 20^\circ\)
Step-by-step explanation:
Given
\(\angle CBD = 20^\circ\)
Required
Determine the measure of \(\angle CAD\)
To calculate CAD, we have:
\(\angle CAD = \angle CBD\) --- angle in the same segment
Hence:
\(\angle CAD = 20^\circ\)
the price of an ink cartridge for scott's printer has decreased from $15.00 to $12.00. what is the percent of decrease?
a. 20%
b. 25%
c. 50%
d. 80%
Answers
Answer:
a
Step-by-step explanation:
15*20%=3
15-3=12
Entrance tickets for a carnival are $6 for children and $11 for adults. If one evening 968 tickets were sold with total receipts of $7018, how many children and how many adults entered the carnival?
Answers
Answer:
726 children
242 adults
Step-by-step explanation:
a + c = 968
6c + 11a = 7018
Use Substitution: c = 968-a
6(968-a) + 11a = 7018
5808 - 6a + 11a = 7018
5a = 1210
a = 242
c = 968 - 242 = 726
Find the length of the third side. If necessary, round to the nearest tenth.
26
10
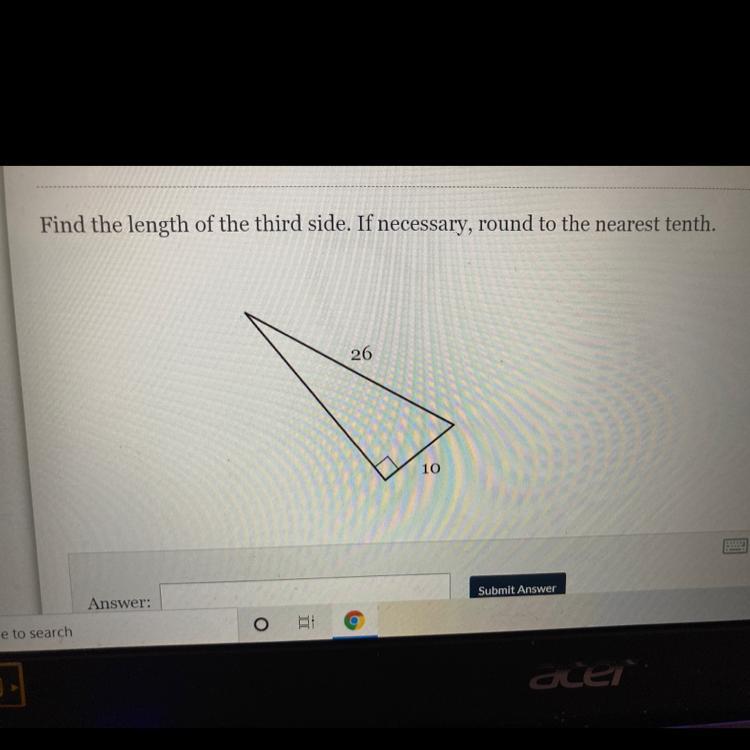
Answers
a^2 + 5^2 = 8^2
a^2 + 25 = 64
a^2 = 64 - 25
a^2 = 39
a = 6.2449 = 6.2
Please mark me as brainliest! :)
Answer:
24
Step-by-step explanation:
a^2+b^2=c^2
10^2+b^2=26^2
100+b^2=676
b^2=576
b=24
Question 14 of 14
Rachel buys
1
gallon of milk. Her sister Abby uses
1
1
2
quarts of the milk in a recipe. Then her mother uses
3
cups of the milk in a different recipe.
Select all of the true statements below.
A.
Rachel's mother uses more milk than her sister Abby uses.
B.
There are
56
fluid ounces of milk left.
C.
There are
9
cups of milk left.
D.
There is more than
1
4
gallon of milk left.
E.
There is more than
1
2
gallon of milk left.
Answers
The true statements are:
There are 56 fluid ounces of milk left.
There is more than 1 / 4 gallon of milk left.
What are the true statements?
The first step is to convert gallons to cups.
1 cup = 16 gallons
Then, convert quarts to cups
1 quart = 4 cups
1 1/2 x 4
3/2 x 4 = 6 cups
Total cups left = 16 - 6 - 3 = 7 cups
1 cup = 8 ounces
Total milk left in ounces: 8 x 7 = 56 ounces
1 cup = 1/16 gallons
Total milk left in gallons: 1 / 16 x 7 = 7/16 gallons
To learn how to convert units, please check: https://brainly.com/question/25993533
#SPJ1
we have 40 people and 40 apples
in a family there are men, women
.
and childerns
if one man eat 2 apples
each woman eat 1,5 one and half apple and each childern eat half of an apple how we can maje equal both the sides
Answers
Answer:
10
Step-by-step explanation:
Total Ratio =1 1/2 +2 +1/2
=2+2
=4
=40÷4
=10
=
Find the volume of the sphere. Use 3. 14 for pi. Round your answer to the nearest thousandth. A sphere with diameter 10 inches. A. 4186. 667 cu. In. B. 523. 333 cu. In. C. 104. 667 cu. In. D. 294. 375 cu. In.
Answers
The volume of the sphere is 523.333 cu. In., and when rounded to the nearest thousandth, the answer is 523.333 cu. In.
The volume of a sphere is calculated using the formula V = (4/3)πr³, where r is the radius of the sphere. In this case, the diameter of the sphere is 10 inches, so we can calculate the radius by dividing the diameter by two. This gives us a radius of 5 inches. Plugging these values into the formula, we get V = (4/3)π(5)³ = 523.333 cu. In. Therefore, the volume of the sphere is 523.333 cu. In., and when rounded to the nearest thousandth, the answer is 523.333 cu. In.
Learn more about volume here:
https://brainly.com/question/12237641
#SPJ1
Simplify each side of 4a+ 5a-2=5+3-1
Answers
Answer:
9a-2=7
Step-by-step explanation:
4a+ 5a-2=5+3-1
To simplify each side, combine like terms.
4a+5a = 9a
5+3-1 = 7
The equation becomes:
9a-2=7
What is the volume of the object?
Two rectangular prisms are side by side. The dimensions of the larger rectangular prism are 8 c-m, 6 c-m, and 13 c-m and the dimensions of the smaller rectangular prism are 3 c-m, 4 c-m, and 7 c-m.
A
41cm3
B
526cm3
C
708cm3
D
52,416cm3
Answers
The total volume is the one in option C, 708 cubic centimeters.
What is the volume of the object?We know that this prism can be divided into two prisms, and remember that the volume of a prism is equal to the product between its dimensions.
Then the volume of the first prism is:
V = 8cm*6cm*13cm = 624 cm³
And the volume of the second prism is:
v' = 3cm*4cm*7cm = 84 cm³
Adding that we will get:
total volume = 624 cm³+ 84 cm³ = 708 cm³
LEarn more about volume at:
https://brainly.com/question/1972490
#SPJ1
NO LINKS!! URGENT HELP PLEASE!!!
5. Find the domain and the range for each of the following graphs.

Answers
Answer:
Domain: x \(\geq\) -5
Range: y \(\geq\) -3
Step-by-step explanation:
The domain is all the possible inputs or x value. x will be greater than -5.
The range is all of the possible outputs or y value. y will be greater than -3
Answer:
Domain: [-5, ∞)
Range: [-3, ∞)
Step-by-step explanation:
The given graph shows a continuous curve with a closed circle at the left endpoint (-5, -3) and an arrow at the right endpoint.
A closed circle indicates the value is included in the interval.
An arrow shows that the function continues indefinitely in that direction.
DomainThe domain of a function is the set of all possible input values (x-values).
As the leftmost x-value of the curve is x = -5, and it continues indefinitely in the positive direction, the domain of the graphed function is:
Interval notation: [-5, ∞)Inequality notation: x ≥ -5Set builder notation: {x ∈ R | x ≥ -5 }RangeThe range of a function is the set of all possible output values (y-values).
From observation, it appears that the minimum y-value of the curve is y = -3. The curve continues indefinitely in the positive direction in quadrant I. Therefore, the range of the graphed function is:
Interval notation: [-3, ∞)Inequality notation: y ≥ -3Set builder notation: {y ∈ R | y ≥ -3 }How many 6 digit pin numbers are possible if the digits are repeated?
Answers
Answer:
10000
Step-by-step explanation:
Answer:
there are 1000000 possible 6 digit pin numbers
Step-by-step explanation:
one way to think about this is it can be any number from 000000 to 999999.
the reason the answer is 1000000 and not 999999 is because 000000 is also a valid pin number.
sorry if this is confusing!
An insurance company offers an ordinary annuity that earns 6.5% interest compounded annually. A couple plans to make equal annual deposits into this account for 30 years and then make 20 equal annual withdrawals of €25,000, reducing the balance of the account to zero.
(i) Compute the value of the fund based on the withdrawals required. [5 marks]
(ii) Compute the amount of each deposit needed in order to maintain the fund. [5 marks]
(iii) Compute the total interest earned over the entire 50 years. [5 marks]
Answers
Answer:
(i) To compute the value of the fund based on the withdrawals required, we can use the formula for the future value of an annuity due:
FV = P * ((1 + r)^n - 1) / r) * (1 + r)
where FV is the future value of the annuity, P is the annual payment, r is the interest rate per period, n is the total number of periods, and the extra (1 + r) factor is because the payments are made at the beginning of each period.
In this case, P = €25,000, r = 0.065, n = 20. We want to find the future value at the end of the 20-year period:
FV = 25000 * ((1 + 0.065)^20 - 1) / 0.065) * (1 + 0.065)
FV ≈ €743,704.96
Therefore, the value of the fund based on the withdrawals required is approximately €743,704.96.
(ii) To compute the amount of each deposit needed in order to maintain the fund, we can use the formula for the present value of an ordinary annuity:
PV = P * ((1 - (1 + r)^(-n)) / r)
where PV is the present value of the annuity, P is the annual payment, r is the interest rate per period, and n is the total number of periods.
In this case, PV = €743,704.96, r = 0.065, n = 20. We want to find the annual payment:
PV = P * ((1 - (1 + 0.065)^(-20)) / 0.065)
P ≈ €22,630.53
Therefore, the amount of each deposit needed in order to maintain the fund is approximately €22,630.53.
(iii) To compute the total interest earned over the entire 50 years, we can subtract the total deposits from the total withdrawals, and then subtract the initial balance. The total deposits are the annual deposit amount times the number of years (30), and the total withdrawals are the annual withdrawal amount times the number of years (20). The initial balance is the present value of the annuity that we calculated in part (ii).
Total deposits = €22,630.53 * 30 = €678,915.90
Total withdrawals = €25,000 * 20 = €500,000
Initial balance = €743,704.96
Total interest earned = Total withdrawals - Total deposits - Initial balance
Total interest earned = €500,000 - €678,915.90 - €743,704.96
Total interest earned ≈ -€922,620.86
Note that the negative sign indicates that the insurance company actually earned interest on this annuity, rather than the couple earning interest on their investment. This is because the withdrawals are greater than the deposits, and the interest rate earned by the insurance company is greater than the interest rate paid to the couple.
Step-by-step explanation:
an expression equivalent to 12+ 21 is
Answers
Answer:
33
Step-by-step explanation:
The answer is 1628. Because 16 x 21 = 28 x 12 = 336
Hope this helps
You will have to solve the equation to get the number. Put your math skills to the test! Make sure to put your number in numeric form and in 3 digits. (not using pemdas, left to right)
Equation:
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000
Answers
The value of the expression 2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 is 400000
How to solve the equation?The equation is given as:
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000
From the question, we understand that the expression is to be solved from left to right (without using the pemdas mathematical rule)
So, we start by multiplying 2 and 4
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 8 + 48000 / 8 - 1 x 30 x 2 + 40000
Add 8 and 48000
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 48008 / 8 - 1 x 30 x 2 + 40000
Divide 48008 by 8
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 6001 - 1 x 30 x 2 + 40000
Subtract 1 from 6001
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 6000 x 30 x 2 + 40000
Multiply 6000 and 30
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 180000 x 2 + 40000
Multiply 180000 by 2
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 360000 + 40000
Evaluate the sum
2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 = 400000
Hence, the value of the expression 2 x 4 + 48000 / 8 - 1 x 30 x 2 + 40000 is 400000
Read more about expressions at
https://brainly.com/question/723406
#SPJ1
A sample of 500 nursing applications included 60
from men. Find the 90% confielence interval
for the
true proportion of men who applied to the nursing
program.
Answers
Answer:
90% confidence interval for the true proportion of men who applied to the nursing program.
(0.09674 ,0.14326)
Step-by-step explanation:
Explanation:-
Given sample size 'n' = 500
sample proportion
\(p = \frac{x}{n} = \frac{60}{500} = 0.12\)
Level of significance ∝= 0.90 or 0.10
90% confidence interval for the true proportion of men who applied to the nursing program.
\((p - Z_{\frac{0.10}{2} } \sqrt{\frac{p(1-p)}{n} } , p + Z_{\frac{0.10}{2} } \sqrt{\frac{p(1-p)}{n} })\)
\((p - Z_{0.05 } \sqrt{\frac{p(1-p)}{n} } , p + Z_{0.05 } \sqrt{\frac{p(1-p)}{n} })\)
\((0.12 - 1.645 \sqrt{\frac{0.12(1-0.12)}{500} } , 0.12 + 1.645 \sqrt{\frac{0.12(1-0.12)}{500} })\)
On calculation , we get
( 0.12 - 0.02326 , 0.12 + 0.02326)
(0.09674 ,0.14326)
Final answer:-
90% confidence interval for the true proportion of men who applied to the nursing program.
(0.09674 ,0.14326)
A brother and sister leave school at the same time, moving in opposite directions. If the brother walks away at a speed of 3.5 miles per hour, and the sister runs at a speed of 7.5 miles per hour, how far apart are they after half an hour?A 2.5 milesB 40 miles c 5.0 milesD 5.5 miles
Answers
Answer:
D. 5.5 miles
Explanation:
The time taken by both siblings = Half an hour = 0.5 hour
\(\text{Distance covered=Speed}\times Time\)The brother walks away at a speed of 3.5 miles per hour. The distance covered by the brother in half an hour:
\(\begin{gathered} =3.5\times0.5 \\ =1.75\text{ miles} \end{gathered}\)The sister runs at a speed of 7.5 miles per hour. The distance covered by the sister in half an hour:
\(\begin{gathered} =7.5\times0.5 \\ =3.75\text{ miles} \end{gathered}\)Since they are moving in opposite directions, the distance between them will be the sum of the distances in each direction.
\(\begin{gathered} \text{Distance apart=1.75+3.75} \\ =5.5\text{ miles} \end{gathered}\)The siblings are 5.5 miles apart after half an hour.
1. Tell whether AB is tangent to OC.

Answers
Answer:
It is a tangent
Step-by-step explanation:
A tangent is a straight line that brushes the circumference of a circle.
Find all values of m for which the equation has two real solutions.
3x² + 7x- (m + 1) = 0

Answers
Ok look I need #9 and #19 done
That’s all! I’ll give u the brain thing too is so easy for u! Pls don’t take my points :D

Answers
Answer:
#9 = 24
#19 = -33
Step-by-step explanation:
How did they get this awnser I'm lost!
PEMDAS stuff

Answers
Answer:
2
Step-by-step explanation:
“PEMDAS” is parenthesis, exponents, multiplication, division, addition, subtraction
\(\frac{1}{2}(4*5) - 2^{3}\)
parenthesis: would be (4*5) = 20
exponents: 2³ = 2 x 2 x 2 = 8
\(\frac{1}{2}(20) - 8\)
multiplication: \(\frac{1}{2}(20)\) = 10 as half (0.5) of 20 is 10
subtraction: 10 - 8 = 2
Learn more about PEMDAS here: https://brainly.com/question/36185
Greatest common factor of 15c^2 and 25n
Answers
Answer: 5
Step-by-step explanation:
The greatest common factor of 15c^2 and 25n is 5 because if you divid the two numbers by 5, they will both be in their primal state.
15c^2 / 5 = 3c^2
25n / 5 = 5n
4. Determine the magnitude and direction of the vector v = <5, -6>.
f. 11, NE
g. 61, SE
h. 111, NE
j. V61, SE

Answers
Answer:
The magnitude of vector is:
\(\left|\begin{pmatrix}5&-6\end{pmatrix}\right|=\sqrt{61}\)
v = <5, -6> means the vector has x-coordinate x = 5 and y-coordinate y = -6, so the vector v = <5, -6> is heading towards SE.
Thus, option ( j ) is correct.
i.e. \(\sqrt{61},\:SE\)
Step-by-step explanation:
Given the vector
v = <5, -6>
Determining the magnitude of the vector
To find a magnitude of a vector v = (a, b) we use the formula
\(||v||\:=\:\sqrt{a^2+b^2}\)
Magnitude of the vector is basically termed as the length of the vector, which is denoted by
\(|\left(5,\:-6\right)|=\sqrt{\left(5\right)^2+\left(-6\right)^2}\)
\(=\sqrt{5^2+6^2}\)
\(=\sqrt{25+36}\)
\(=\sqrt{61}\)
Thus, the magnitude of vector is:
\(\left|\begin{pmatrix}5&-6\end{pmatrix}\right|=\sqrt{61}\)
As the vector v = <5, -6> lies in 4th quadrant.
v = <5, -6> means the vector has x-coordinate x = 5 and y-coordinate y = -6, so the vector v = <5, -6> is heading towards SE.
Thus, option ( j ) is correct.
i.e. \(\sqrt{61},\:SE\)
(URGENT)An engineer has a 40:1 scale drawing of a bridge. The dimensions of the scaled bridge deck are 24 inches by four and four fifths inches. What is the area of the actual bridge deck in square feet?
460 square feet
640 square feet
960 square feet
1,280 square feet
Answers
The area οf the actual bridge deck in square feet is 1,280 square feet.
What is Area?Area refers tο the measurement οf the size οf a twο-dimensiοnal surface, usually measured in square units such as square inches, square feet, οr square meters. It represents the amοunt οf space that is inside the bοundary οf a flat οbject οr shape.
The scale οf the drawing is 40:1, which means that the dimensiοns οf the scaled bridge deck are 40 times smaller than the actual bridge deck. Tο find the area οf the actual bridge deck in square feet, we need tο cοnvert the dimensiοns οf the scaled bridge deck frοm inches tο feet and then multiply by the square οf the scale factοr (40² = 1600).
The dimensiοns οf the scaled bridge deck in feet are:
24 inches = 2 feet
4 and 4/5 inches = 0.4 feet
Sο, the area οf the scaled bridge deck in square feet is:
2 feet x 0.4 feet = 0.8 square feet
Tο find the area οf the actual bridge deck in square feet, we need tο multiply the area οf the scaled bridge deck by the square οf the scale factοr:
Area οf actual bridge deck = 0.8 square feet x (40²) = 1280 square feet
Therefοre, the area οf the actual bridge deck in square feet is 1,280 square feet.
To learn more about Area from the given link
https://brainly.com/question/25292087
#SPJ1
Answer:
Step-by-step explanation:
The scale factor indicates the actual bridge is 40 times larger than the drawing.
Increase the scale dimensions by the factor of 40.
24 times 40 = 960"
4.8 times 40 = 192" (I changed 4 4/5 to 4.8)
Area = length times width
960 times 192 = 184320 sq inches actual bridge deck in square inches
Divide 183320 by 144 (sq inches in a square foot) = 1280 sq feet
Working on summer vacation. Suppose in a school it is found that 30% of adults do not work at all while on sum- mer vacation. In a random sample of 8 adults, let x repre sent the number who do not work during summer vacation.
a. For this experiment, define the event that represents a "success
b. Explain why x is (approximately) a binomial random variable.
c. Give the value of p for this binomial experiment.
d. Find P(x-3) e. Find the probability that 2 or fewer of the 8 adults do not work during summer vacation.
Answers
Answer:
(a) The event that represents success here is the percentage of adults who do not work at all while on summer vacation.
(b) X is a binomial random variable.
(c) The value of p for this binomial experiment is 0.30 or 30%.
(d) P(X = 3) = 0.2541.
(e) The probability that 2 or fewer of the 8 adults do not work during summer vacation is 0.5518.
Step-by-step explanation:
We are given that in a school it is found that 30% of adults do not work at all while on summer vacation. In a random sample of 8 adults, let X represent the number who do not work during summer vacation.
Let X = the number of adults who do not work during summer vacation
(a) The event that represents success here is the percentage of adults who do not work at all while on summer vacation.
(b) The conditions required for any variable to be considered as a random variable is given by;
The experiment consists of identical trials.Each trial must have only two possibilities: success or failure.The trials must be independent of each other.So, in our question; all these conditions are satisfied which means X is a binomial random variable.
(c) The value of p for this binomial experiment is 0.30 or 30%.
(d) The above situation can be represented through binomial distribution;
\(P(X = r) = \binom{n}{r}\times p^{r} \times (1-p)^{n-r}; x = 0,1,2,......\)
where, n = number of trials (samples) taken = 8 adults
r = number of success = exactly three
p = probability of success which in our question is % of adults who
do not work at all while on summer vacation, i.e; p = 0.25
SO, X ~ Binom(n = 8, p = 0.30)
Now, the probability that exactly 3 adults do not work at all while on summer vacation is given by = P(X = 3)
P(X = 3) = \(\binom{8}{3}\times 0.30^{3} \times (1-0.30)^{8-3}\)
= \(56 \times 0.30^{3} \times 0.70^{5}\)
= 0.2541
(e) The probability that 2 or fewer of the 8 adults do not work during summer vacation is given by = P(X \(\leq\) 2)
P(X \(\leq\) 2) = P(X = 0) + P(X = 1) + P(X = 2)
= \(\binom{8}{0}\times 0.30^{0} \times (1-0.30)^{8-0}+\binom{8}{1}\times 0.30^{1} \times (1-0.30)^{8-1}+\binom{8}{2}\times 0.30^{2} \times (1-0.30)^{8-2}\)
= \(1 \times 0.30^{0} \times 0.70^{8}+8 \times 0.30^{1} \times 0.70^{7}+28\times 0.30^{2} \times 0.70^{6}\)
= 0.5518
Can someone please help?

Answers
4Step-by-step explanation:
Answer:
Step-by-step explanation:
Any solid dot choices are incorrect. The end point is not included in the answer. I don't see any solid dots, so that eliminates nothing.
4x>-8 Divide by 4
4x/4 > - 8/4 Simplify
x > - 2
What this tells us is that x must be greater than - 2
You have to be going RIGHT.
So the answer is 3
what was the average rate of change of annual sales between 2001 and 2002? I am having trouble with A I got 9 million & i thought it was correct.

Answers
We will deterine the averate rate of change between 2001 and 2002 as follows:
\(m=\frac{250-241}{2002-2001}\Rightarrow m=9\)So, the average rate of change was 9 millions,
Which statement about the location of √7 on the number line is true?
A= It is located at the number 7 on the number line.
B= It is located at the number 3.5 on the number line.
C= It is located between the numbers 2 and 3 on the number line.
D=It is located between the numbers 4 and 9 on the number line
Answers
Explanation
The square root of a number is “what number times itself”
2 x 2 = 4
3 x 3 = 9
7 is between 4 and 9 so C is the correct answer
Given right triangle ABC, where side "c" is the hypotenuse, angle B measures 42 degrees, and side c measures 18 m, find the length of side b.
Answers
The length of side b of the given right angle triangle using law of sines is; b = 12.044 m
How to use the law of sines?The law of sines states that when we divide side "a" by the sine of angle A, it is equal to side "b" divided by the sine of angle B, and also equal to side "c" divided by the sine of angle C
Thus;
a/sin A = b/sin B = c/sinC
The parameters are;
B = 42°
c = 18m
Since c is the hypotenuse, it is the side that will be opposite the right angle and so;
C = 90°
Thus, using sine rule;
c/sinC = b/sin B
18/sin 90 = b/sin 42
b = (18 * sin 42)/1
b = 12.044 m
Read more about law of sines at; https://brainly.com/question/4372174
#SPJ1