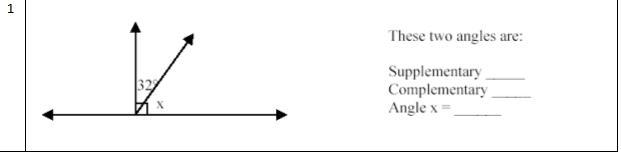
Answers
Answer: Complementary
x=58
Step-by-step explanation:
Related Questions
Two linear functions are represented in different ways. One linear function is represented by the equation y =−3x.
Answers
Answer: Y = -3x
Step-by-step explanation:not needed
continuinty
Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a f(x) = x² + 5x 2x + 1 a = 2
Answers
The function is continuous by the property of limits.
Given data ,
To show that the function f(x) = x^2 + 5x / (2x + 1) is continuous at a = 2:
The value of the function at x = 2 is equal to the limit.
Let's proceed step by step:
The function is defined at x = 2:
To check this, substitute x = 2 into the function:
f(2) = (2² + 5(2)) / (2(2) + 1)
= (4 + 10) / (4 + 1)
= 14 / 5
So, f(2)=14/5 and is defined.
The limit of the function as x approaches 2 exists:
We need to evaluate the limit of f(x) as x approaches 2.
lim(x→2) (x² + 5x) / (2x + 1)
We can simplify the expression by directly substituting x = 2 into the function:
lim(x→2) (x² + 5x) / (2x + 1) = (2² + 5(2)) / (2(2) + 1) = 14 / 5
Therefore, the limit of f(x) as x approaches 2 exists and is equal to 14/5.
The value of the function at x = 2 is equal to the limit:
We have already computed f(2) = 14/5, and the limit lim(x→2) f(x) = 14/5.
Since the value of the function at x = 2 (14/5) is equal to the limit as x approaches 2 (14/5), we can conclude that the function is continuous at x = 2.
Hence, satisfying all three conditions, we have shown that the function f(x) is continuous at x = 2.
To learn more about property of limits click :
https://brainly.com/question/30339385
#SPJ4
The complete question is attached below :
Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a f(x) = (x² + 5x) / (2x + 1) a = 2

(c) दिइएको त्रिभुजमा कुन-कुन अनुरुप छन् ?
Which triangles are congruent in the given
triangles?
A
P
F
E
809
E
cm
180°
70°
C0 10cm
B
R
D
Answers
Please help me with this question!

Answers
Answer:
part 2 of 3 means is it ans
Step-by-step explanation:
I don't understand ur question can u explain me then I I will ans
The length of a rectangular garden is three feet less than twice its width. If the perimeter of the garden is 42 fett, what is its length?
Answers
Answer:
13 feet
Step-by-step explanation:
If the length is 3 less than 2x the width, you can set up the equation 2(2w-3) + 2(w) = 72 and solve. That gives you w = 8. Lastly plug it in and that gives you 13.
Which of Polygons B, C, D, E, and F are similar to Polygon A? Select all that apply. Recall
that similar means same shape and different sizes. The figures do not need to be
oriented the same way.

Answers
Answer: A, D, F
The guy above me is wrong.
The rate of consumption of oil in the United States during the 1980s (in billions of barrels per year) is modeled by the function C(t) = 27.08e', where t is the number of years after January 1, 1980. Find the total consumption of oil in the United States from January 1, 1980 to January 1, 1990.
Answers
the total consumption of oil in the United States from January 1, 1980, to January 1, 1990 is approximately 596,533.7 billion barrels.
To find the total consumption of oil in the United States from January 1, 1980 to January 1, 1990, we need to integrate the given function\(C(t) = 27.08e^t\)with respect to time t, over the interval [0, 10], where t is measured in years.
The integral of the function is:
∫\((27.08e^t) dt\)
To solve this integral, we use the fact that the integral of\(e^t\) is \(e^t\)itself. Thus, we get:
27.08∫\(e^t dt = 27.08e^t\)
Now, we need to evaluate the definite integral over the interval [0, 10]:
\(27.08e^t\)| from 0 to 10 =\(27.08(e^{10} - e^0)\)
As e^0 = 1, the expression simplifies to:
\(27.08(e^{10} - 1)\)
Now, we can calculate the value of the expression:
\(27.08(e^{10} - 1) =27.08(22026.47 - 1) = 27.08 * 22025.47 =596533.7\)
Thus, the total consumption of oil in the United States from January 1, 1980, to January 1, 1990 is approximately 596,533.7 billion barrels.
learn more about integral
https://brainly.com/question/18125359
#SPJ11
S
You have $18 to spend on lip balm and hand sanitizer. The equation 1.5x + 2.5y = 18 represents this situation, where x is tubes of
lip balm and y is bottles of hand sanitizer. How many tubes of lip balm can you buy when you do not buy any bottles of hand
sanitizer?
Answers
Answer:
(1.5×5) + (2.5×4)
Step-by-step explanation:
if 1.5 + 2.5 is 4.0, and you have $18 and you would see how many times 4 can go into 18 (18÷4) which has four times then you have $2 left so you can get another lip balm so x equals 5 and Y equals 4. I hope this helps! :D
(a) Given an initial condition for y0, answer the following questions, where yt is the random variable at time t,ε is the error, t is also the time trend in (iii):
(i) find the solution for yt, where yt=yt−1+εt+0.3εt−1.
(ii) find the solution for yt, and the s-step-ahead forecast Et[yt+s] for yt=1.2yt−1+εt and explain how to make this model stationary.
(iii) find the solution for yt, and the s-step-ahead forecast Et[yt+s] for yt=yt−1+t+εt and explain how to make this model stationary.
Answers
(i) To find the solution for yt in the given equation yt = yt−1 + εt + 0.3εt−1, we can rewrite it as yt - yt−1 = εt + 0.3εt−1. By applying the lag operator L, we have (1 - L)yt = εt + 0.3εt−1.
Solving for yt, we get yt = (1/L)(εt + 0.3εt−1). The solution for yt involves lag operators and depends on the values of εt and εt−1. (ii) For the equation yt = 1.2yt−1 + εt, to find the s-step-ahead forecast Et[yt+s], we can recursively substitute the lagged values. Starting with yt = 1.2yt−1 + εt, we have yt+1 = 1.2(1.2yt−1 + εt) + εt+1, yt+2 = 1.2(1.2(1.2yt−1 + εt) + εt+1) + εt+2, and so on. The s-step-ahead forecast Et[yt+s] can be obtained by taking the expectation of yt+s conditional on the available information at time t.
To make this model stationary, we need to ensure that the coefficient on yt−1, which is 1.2 in this case, is less than 1 in absolute value. If it is greater than 1, the process will be explosive and not stationary. To achieve stationarity, we can either decrease the value of 1.2 or introduce appropriate differencing operators.
(iii) For the equation yt = yt−1 + t + εt, finding the solution for yt and the s-step-ahead forecast Et[yt+s] involves incorporating the time trend t. By recursively substituting the lagged values, we have yt = yt−1 + t + εt, yt+1 = yt + t + εt+1, yt+2 = yt+1 + t + εt+2, and so on. The s-step-ahead forecast Et[yt+s] can be obtained by taking the expectation of yt+s conditional on the available information at time t.
To make this model stationary, we need to remove the time trend component. We can achieve this by differencing the series. Taking first differences of yt, we obtain Δyt = yt - yt-1 = t + εt. The differenced series Δyt eliminates the time trend, making the model stationary. We can then apply forecasting techniques to predict Et[Δyt+s], which would correspond to the s-step-ahead forecast Et[yt+s] for the original series yt.
Learn more about model here: brainly.com/question/19426210
#SPJ11
Please help me with this

Answers
Answer:
x = 23
Step-by-step explanation:
if line j is parallel to line k then
5x + 9 + 33 + x = 180 add like terms
6x + 42 = 180 subtract 42 from both sides
6x = 138 divide both sides by 6
x = 23
x+y=5
5x - 3y - 17
answer
Answers
9514 1404 393
Answer:
(x, y) = (4, 1)
Step-by-step explanation:
We assume you want to solve ...
x +y = 55x -3y = 17Multiply the first equation by 3 and add the second:
3(x +y) +(5x -3y) = 3(5) +(17)
8x = 32 . . . . . . simplify
x = 4 . . . . . . . . .divide by 8
4 +y = 5 . . . . . . substitute into the first equation
y = 1 . . . . . . . . .subtract 4
The solution is (x, y) = (4, 1).
I really need help I'm to the point of tears please help
A line that includes the points (g,–7) and (7,2) has a slope of –9. What is the value of g?
Answers
Answer:
g = 8
Step-by-step explanation:
The image below shows when g equals 8 and creates the point (8,-7), both that and (7,2) fall on the line of the equation y = -9x + 65, which has a slope of -9.

a newborn baby has extremely low birth weight (elbw) if it weighs less than 1000 grams. a study of the health of such children in later years examined that such children's weight follows a normal distribution with a mean of 810 grams and a standard deviation of 40 grams. what is the mean and standard deviation of the sampling distribution of the average weight for simple random samples (srs) of 100 children who had been born with elbw?
Answers
The mean of the sampling distribution is still 810 grams, which is the same as the population mean. The standard deviation of the sampling distribution is 4 grams.
The mean of the sampling distribution for the average weight of a simple random sample can be considered an unbiased estimator of the population mean. In this case, since the population mean is 810 grams, the mean of the sampling distribution remains the same.
The standard deviation of the sampling distribution, on the other hand, is influenced by the sample size. The formula for the standard deviation of the sampling distribution of the sample mean is given by the population standard deviation divided by the square root of the sample size. In this case, the population standard deviation is 40 grams, and the sample size is 100. Therefore, the standard deviation of the sampling distribution is calculated as 40 grams divided by the square root of 100, which is 4 grams.
In summary, the mean of the sampling distribution for the average weight of simple random samples of 100 children born with ELBW is 810 grams, and the standard deviation is 4 grams.
Learn more about standard deviation here:
https://brainly.com/question/29115611
#SPJ11
Find the perimeter of the image below:
37 units
38 units
39 units
40 units

Answers
Answer:
154
Step-by-step explanation:
add all of tham together to get it
In a baseball game, a pop fly is hit, and its height in meters relative to time in seconds is modeled by the function h(t)=4.9t^2+8t+1
a.) What direction does it open?
b.) For how many seconds is the ball in the air?
c.) When does the ball begin coming down after being hit?
d.) What is the maximum height of the baseball?
Answers
a.) The pop fly opens upward.
b.) The ball is in the air for approximately 1.63 seconds.
c.) The ball begins coming down after 1.63 seconds.
d.) The maximum height of the baseball is 21.27 meters.
a.) The quadratic function h(t) = 4.9t^2 + 8t + 1 is in the form of h(t) = a(t - b)^2 + c, where a, b, and c are constants. Since the coefficient of the squared term (a) is positive, the graph of the function opens upward, indicating that the pop fly opens upward.
b.) The ball is in the air as long as it takes for it to hit the ground, which occurs when h(t) = 0. To find the time it takes for the ball to hit the ground, we can solve the quadratic equation 4.9t^2 + 8t + 1 = 0 using the quadratic formula. The solutions are approximately -0.19 and -1.44, but we discard the negative solution since time cannot be negative. Therefore, the ball is in the air for approximately 1.63 seconds.
c.) The ball begins coming down after it reaches its maximum height, which occurs at the vertex of the parabola. To find the time when the ball reaches its maximum height, we can use the formula t = -b/2a, where a and b are the coefficients of the squared and linear terms, respectively. Plugging in the values from the function h(t), we get t = -8/(2*4.9) = -0.8163 seconds. Since time cannot be negative, we discard this solution and take the positive value of t, which is 1.63 seconds. Therefore, the ball begins coming down after 1.63 seconds.
d.) The maximum height of the baseball is the y-coordinate of the vertex of the parabola, which we can find by plugging in the value of t we just found. Plugging t = 1.63 into the function h(t), we get h(1.63) = 4.9(1.63)^2 + 8(1.63) + 1 = 21.27 meters. Therefore, the maximum height of the baseball is 21.27 meters.
Learn more about Maximum:
brainly.com/question/17467131
#SPJ11
Find the exact value of sin(α β), if sinα= 3 5 and sinβ= 5 13, with α in quadrant i and β in quadrant
Answers
The exact value of sin(α + β) is -16/65.
To find the exact value of sin(α + β), we can use the trigonometric identities and the given information about the values of sinα and sinβ.
We are given:
sinα = 3/5 (α in quadrant I)
sinβ = 5/13 (β in quadrant II)
Let's use the sum formula for sine:
sin(α + β) = sinα * cosβ + cosα * sinβ
To evaluate sinα, we need to find cosα using the Pythagorean identity:
sin²α + cos²α = 1
Given sinα = 3/5, we can solve for cosα:
(3/5)² + cos²α = 1
9/25 + cos²α = 1
cos²α = 1 - 9/25
cos²α = 16/25
cosα = ± √(16/25)
cosα = ± 4/5
Since α is in quadrant I, cosα is positive:
cosα = 4/5
Similarly, we need to find cosβ using the Pythagorean identity:
sin²β + cos²β = 1
Given sinβ = 5/13, we can solve for cosβ:
(5/13)² + cos²β = 1
25/169 + cos²β = 1
cos²β = 1 - 25/169
cos²β = 144/169
cosβ = ± √(144/169)
cosβ = ± 12/13
Since β is in quadrant II, cosβ is negative:
cosβ = -12/13
Now, substitute the values of sinα, cosα, sinβ, and cosβ into the sum formula for sine:
sin(α + β) = (3/5) * (-12/13) + (4/5) * (5/13)
sin(α + β) = -36/65 + 20/65
sin(α + β) = -16/65
Therefore, the exact value of sin(α + β) is -16/65.
for such more question on exact value
https://brainly.com/question/27746495
#SPJ8
A dog breeder breeds both dalmations and terriers.
1/4 of the dogs they breed are terriers.
What is the ratio of dalmations to terriers bred?
Answers
Answer:
\(\frac{3}{4} :\frac{1}{4}\)
Step-by-step explanation:
Given that A dog breeder breeds both dalmatians and terriers. \(\frac{1}{4}\) of the dogs they breed are terriers. The ratio of dalmatians to terriers bred is given as 3:1.
Ratio is the quantitative relation between two amounts showing the number of times one value contains or is contained within the other.
Given in the question,
Let the dog breeder breed x dogs in total
\(\frac{1}{4}\) of the dogs are of breed terriers.
Number of terrier dogs = \(\frac{x}{4}\)
Number of dalmatian dogs = \(x - \frac{x}{4} = \frac{3x}{4}\)
Ratio of dalmatian dogs to terrier dogs = \(\frac{Number \ of \ dalmatian \ dogs}{number \ of \ terrier \ dogs } = \frac{\frac{3x}{4} }{\frac{x}{4} } = \frac{3}{1}\)
Learn more about ratio here
https://brainly.com/question/30932604
#SPJ2
solve for x. -3x = 6
Answers
Answer:
x=-2
Step-by-step explanation:
Divide each side by -3.
-3x = 6
/-3 = /-3
x=-2
!!!!!!!!!HELLLLLPPPP!!!!!!
Find the maximum and minimum values. You will want to draw a graph to determine the intersections of the constraints below.
f=2x + 5y, subject to the constraints
3x + 2y ≤ 6,
-2x + 4y ≤ 8,
x 20,
y 20.
12-²
Maximum: 4: Minimum: 4
12-
Maximum: 4: Minimum: 0
Maximum: 10; Minimum: 0
13-
Maximum: 4: Minimum: 0

Answers
Answer:
maximum 4 Mimimum I'm 0 or maximum 10 minimum 0
What i the lope of a line perpendicular to the line whoe equation i 3x-6y=90. Fully implify your anwer
Answers
The slope of line perpendicular to line 3x - 6y = 90 is -2.
Slope-Intercept form of equation => y = mx + c
Slope = m
Given equation,
3x - 6y = 90
x - 2y = 30
2y = x - 30
y = x/2 - 15
y = (1/2)x + (-15)
Here, slope = m1
= 1/2
For line perpendicular slope will be negative reciprocal of the slope of given line.
Therefore, slope of other line = m2
= -1/m1
= -2
Hence, slope of line perpendicular to line 3x - 6y = 90 is -2.
To learn more about slope here:
https://brainly.com/question/3605446
#SPJ4
NO LINKS PLS! Simplify 6 - (-2) - 3(-5).
Answers
Hope this helps!
Have a great day!
Consider the series One-fourth, StartFraction 1 Over 16 EndFraction + StartFraction 1 Over 64 EndFraction + StartFraction 1 Over 256 EndFraction + ellipsis
Which expression defines Sn?

Answers
Answer:
C, I got it right
Step-by-step explanation:
The two major types of series are the arithmetic series and the geometric series. The arithmetic series is characterized by common difference, while the geometric series has common ratio between two successive terms.
The sum of the given series is:
\(\lim_{n \to \infty} \frac{1}{3}(1 - \frac{1}{4}^n )\)
The given series is a geometric series. So, we first calculate the common ratio (r) using:
\(r = T_2 \div T_1\)
From the series, we have:
\(T_1 = \frac{1}{4}\)
\(T_2 = \frac{1}{16}\)
So, the equation becomes
\(r = \frac{1}{16} \div \frac{1}{4}\)
Rewrite as product
\(r = \frac{1}{16} * \frac{4}{1}\)
\(r = \frac{1}{4}\)
The formula to calculate the sum of a geometric series of is:
\(S_n = \frac{a(1 - r^n )}{1-r}\)
Where
\(a = T_1 =\frac{1}{4}\) -- the first term
\(S_n = \frac{\frac{1}{4}(1 - \frac{1}{4}^n )}{1-\frac{1}{4}}\)
Simplify the denominator
\(S_n = \frac{\frac{1}{4}(1 - \frac{1}{4}^n )}{\frac{3}{4}}\)
Divide 1/4 by 3/4
\(S_n = \frac{1}{3}(1 - \frac{1}{4}^n )\)
We can conclude that, the sum of the series is:
\(S_n = \lim_{n \to \infty} \frac{1}{3}(1 - \frac{1}{4}^n )\)
Read more at:
https://brainly.com/question/21087466
I will give BRAINLIEST to the correct answer

Answers
Answer:
<PCH+<HCK=180-DEGREE BEING IN A STRAIGHT LINE.
3M+58+8M+155=180
11M=180-213
11M=-33
M=-3
SO,
<PCH
3M+58
=3*(-3)+58
=58-9
=49-DEGREE
Given s(t)=3t
2
+3t, where s(t) is in feet and t is in seconds, find each of the following. a) v(t) b) a(t) c) The velocity and acceleration when t=4sec
Answers
The velocity function v(t) is 6t + 3. The acceleration function a(t) is constant and equal to 6. When t = 4 sec, the velocity is 27 ft/s and the acceleration is 6 ft/s^2.
To find the velocity and acceleration, we need to differentiate the position function s(t) with respect to time t.a) Velocity (v(t)): The velocity is the derivative of the position function s(t) with respect to time t.v(t) = d/dt [s(t)]
Given s(t) = 3t^2 + 3t, we can differentiate it to find the velocity:
v(t) = d/dt [3t^2 + 3t]
To differentiate, we apply the power rule of differentiation: v(t) = 6t + 3
Therefore, the velocity function v(t) is 6t + 3.
b) Acceleration (a(t)): The acceleration is the derivative of the velocity function v(t) with respect to time t. a(t) = d/dt [v(t)]
Given v(t) = 6t + 3, we can differentiate it to find the acceleration:
a(t) = d/dt [6t + 3]
The derivative of a constant term is zero, so the derivative of 3 is 0:
a(t) = 6
Therefore, the acceleration function a(t) is constant and equal to 6.
c) Velocity and acceleration when t = 4 sec:
To find the velocity and acceleration at t = 4 seconds, we substitute t = 4 into the respective functions: At t = 4 sec: v(4) = 6(4) + 3
v(4) = 24 + 3
v(4) = 27 ft/s ,a(4) = 6
Therefore, when t = 4 sec, the velocity is 27 ft/s and the acceleration is 6 ft/s^2.
Learn more about differenetiation here :
https://brainly.com/question/13958985
#SPJ11
The area of a rectangle is given below.
If one of the sides is length 2s units, find the perimeter in terms of s.
A = (2s squared – 4s) square units
Answers
Answer:
Rectangle
ABCD
LMNO
PQRS
Area
8 sq. cm
12 sq. cm
6 sq. cm
Length
4 cm
4 cm
2 cm
Breadth
2 cm
3 cm
3 cm
Length × Breadth
4 cm × 2 cm = 8 cm2
4 cm × 3 cm = 12 cm2
2 cm × 3 cm = 6 cm2
In each case we observe the length × breadth = Area of the rectangle.
Therefore, area of rectangle = length × breadth = l × b sq. units
From the above multiplication, we get the following facts:
Length of the rectangle = Area of the RectangleBreadth of the Rectangle
Breadth of the rectangle = Area of the RectangleLength of the Rectangle
Ricardo can type 39 words per minute. Estimate the number of words he can type in 18 minutes.
400
600
300
800
Answers
Answer: 702
Step-by-step explanation: 39 times 18
What is the SLOPE of the line that goes through the points (20,-3) and
(-16.-3)?

Answers
Answer:
0
Step-by-step explanation:
m=y2-y1
____
x2-x1
m=-3-(-3) =(-3+3)/(-36) =0/-36=0
_____
-16-20
What is the circumference of the following circle?

Answers
Answer:
C = 2pi(r)
= 2pi(5)
≈ 31.416
≈ 31.4
Answer:
Hello! answer: 31.4
Step-by-step explanation:
I'm using 3.14 for pi and
To find circumference you just have to do diameter × pi or radius × 2 × pi since we have the radius we can just do radius × 2 × pi so
5 × 2 × 3.14 = 31.4 so our circumfrence is 31.4 Hope that helps!!
73 in.
55 in.
b
What is the length of the missing leg? If necessary, round to the nearest tenth.
b =
inches

Answers
Answer:
48 (rounded to 10).....
Which statement is not always true when
△ABC ≅ △ XYZ
1. BC ≅ YZ
2. CA ≅ XY
3. ∠CAB ≅ ∠ZXY
4. ∠BCA ≅ ∠YZX
Answers
If two triangles are congruent, it means that all corresponding sides and angles are equal. Therefore, all of the statements are always true when △ABC ≅ △ XYZ.
When we say that two triangles, △ABC and △XYZ, are congruent, we mean that they have exactly the same size and shape. This implies that all corresponding sides and angles of the two triangles are equal.
For example, if we say that △ABC ≅ △XYZ, then we know that side AB is equal in length to side XY, side AC is equal in length to side XZ, and side BC is equal in length to side YZ. Additionally, we know that angle A is equal in measure to angle X, angle B is equal in measure to angle Y, and angle C is equal in measure to angle Z.
Therefore, all of the statements in the original question are always true when △ABC ≅ △XYZ because congruence means that all corresponding sides and angles of the two triangles are equal.
Learn more about triangles from
https://brainly.com/question/1058720
#SPJ11