Answers
The height of of the center support that is perpendicular to the ground is 63 feet.
Calculating the height of the center supportFrom the question, we are to calculate the height of the center support shown in the diagram.
In the diagram,
The perpendicular height divides the triangle into two right triangles
Thus, we can determine the height of the center support by using the Pythagorean theorem.
From the Pythagorean theorem, we can write that
65² = h² + (1/2 × 32)²
4225 = h² + (16)²
4225 = h² + 256
h² = 4225 - 256
h² = 3969
h = √3969
h = 63 feet
Hence,
The height of of the center support is 63 feet.
Learn more on Calculating the height here: https://brainly.com/question/73194
#SPJ1
Related Questions
Ty is a landscape architect. He needs to find the value of x in meters so that the sum of the areas of the patio, herb garden, and flower garden is 25% of the area of the entire rectangle. What in the area in square meters of the patio?

Answers
By using this value of x in the formula we previously discovered, we can get the patio's area Patio's size is equal to x2 + 4x + 4 = ((1 + 7)/3)2 + 4((1 + 7)/3) + 4 = 4.72 square meters.
What is a square's area?A square is a 2D shape with equal-sized sides on each side. The area would be length times width, which is equal to side side because all the sides are equal. As a result, a square's area is side square.
Let's first find the area of the entire rectangle:
A = lw = (3x + 6)(2x + 4) = 6x² + 30x + 24
Area of patio = (x + 2)² = x² + 4x + 4
Area of herb garden = (2x + 2)(x + 4) = 2x² + 10x + 8
Area of flower garden = (3x + 4)(x + 4) = 3x² + 16x + 16
Sum of areas = x² + 4x + 4 + 2x² + 10x + 8 + 3x² + 16x + 16
= 6x² + 30x + 28
0.25(6x² + 30x + 24) = 6x² + 30x + 28
Simplifying and solving for x, we get:
1.5x² - x - 1 = 0
Using the quadratic formula, we find that:
x = (1 ± √7)/3
x = (1 + √7)/3
To know more about square visit:-
https://brainly.com/question/14198272
#SPJ1
The area in square meters of the patio is 850 square meters.
What is a rectangle?
A rectangle is a geometric shape that has four sides and four right angles (90 degrees) with opposite sides being parallel and equal in length.
Let's start by calculating the total area of the rectangle:
Area of rectangle = length x width = 100m x 40m = 4000 square meters
Now, let's denote the width of the herb garden as x meters. Then, the length of the herb garden would be 10 meters.
The area of the herb garden would be:
Area of herb garden = length x width = 10m x x = 10x square meters
The area of the patio can be calculated as:
Area of patio = (100 - x) x (40 - 2x) square meters
(100 - x) is the length of the patio, and (40 - 2x) is the width of the patio, since the herb garden takes up x meters of the width.
The area of the flower garden can be calculated by subtracting the area of the rectangle, the herb garden, and the patio from each other:
Area of flower garden = 4000 - 10x - (100 - x) x (40 - 2x) square meters
Now, we need to find the value of x so that the sum of the areas of the patio, herb garden, and flower garden is 25% of the area of the entire rectangle. In other words:
Area of herb garden + Area of patio + Area of flower garden = 0.25 x Area of rectangle
10x + (100 - x) x (40 - 2x) + 4000 - 10x = 0.25 x 4000
Simplifying this equation, we get:
-2x^2 + 30x + 1000 = 1000
-2x^2 + 30x = 0
-2x(x - 15) = 0
Therefore, x = 0 or x = 15. Since x cannot be 0 (since the herb garden would have no width), the value of x must be 15 meters.
Now we can calculate the area of the patio:
Area of patio = (100 - x) x (40 - 2x) = (100 - 15) x (40 - 2(15)) = 850 square meters
Therefore, the area in square meters of the patio is 850 square meters.
To learn more about rectangle from the given link:
https://brainly.com/question/29123947
#SPJ1
If Fx) = x-5 and G(x) = x2 , what is G(F(x))?

Answers
Explanation:
Given the functions
f(x) = x-5
G(x) = x^2
We are to find the composite function G(f(x))
Jeff is 6 feet 2 inches tall. Give Jeff's height in inches
Answers
Answer:
74 inches
Step-by-step explanation:
1ft = 12 inches
6* 12 = 72
72 + 2 = 74 inches
I need help asap plssss

Answers
Answer:
x = -4
Step-by-step explanation:
(x - 5) (x + 4) = x^2 + 4x
If you expand this, you get:
x^2 - x - 20 = x^2 + 4x
graph similar terms together, the x^2 disappears:
-20 = 5x
x = -20/5 = -4
For her 1st birthday Maymay's parents invested $12,000.00 in an 13-year certificate for her that pays 10% compounded every 2 months. How much is the certificate worth on Maymay's 14 birthday? If needed, round to 2 decimal places.
Answers
Answer:
Step-by-step explanation:
Since the certificate pays 10% compounded every 2 months, the monthly interest rate is 10%/6 = 1.67%. The total number of compounding periods over the 13-year period is 13 years x 12 months/year x 1 compounding period/2 months = 78 compounding periods.
Using the formula for the future value of a present sum with compound interest:
FV = PV x (1 + r)^n
where FV is the future value, PV is the present value, r is the interest rate per period, and n is the total number of periods, we can find the value of the certificate on Maymay's 14th birthday:
FV = $12,000 x (1 + 0.0167)^78
FV = $12,000 x 2.6495
FV = $31,794.00
Therefore, the certificate will be worth $31,794.00 on Maymay's 14th birthday.
Hopes that helps :)
Please answer this question now in two minutes
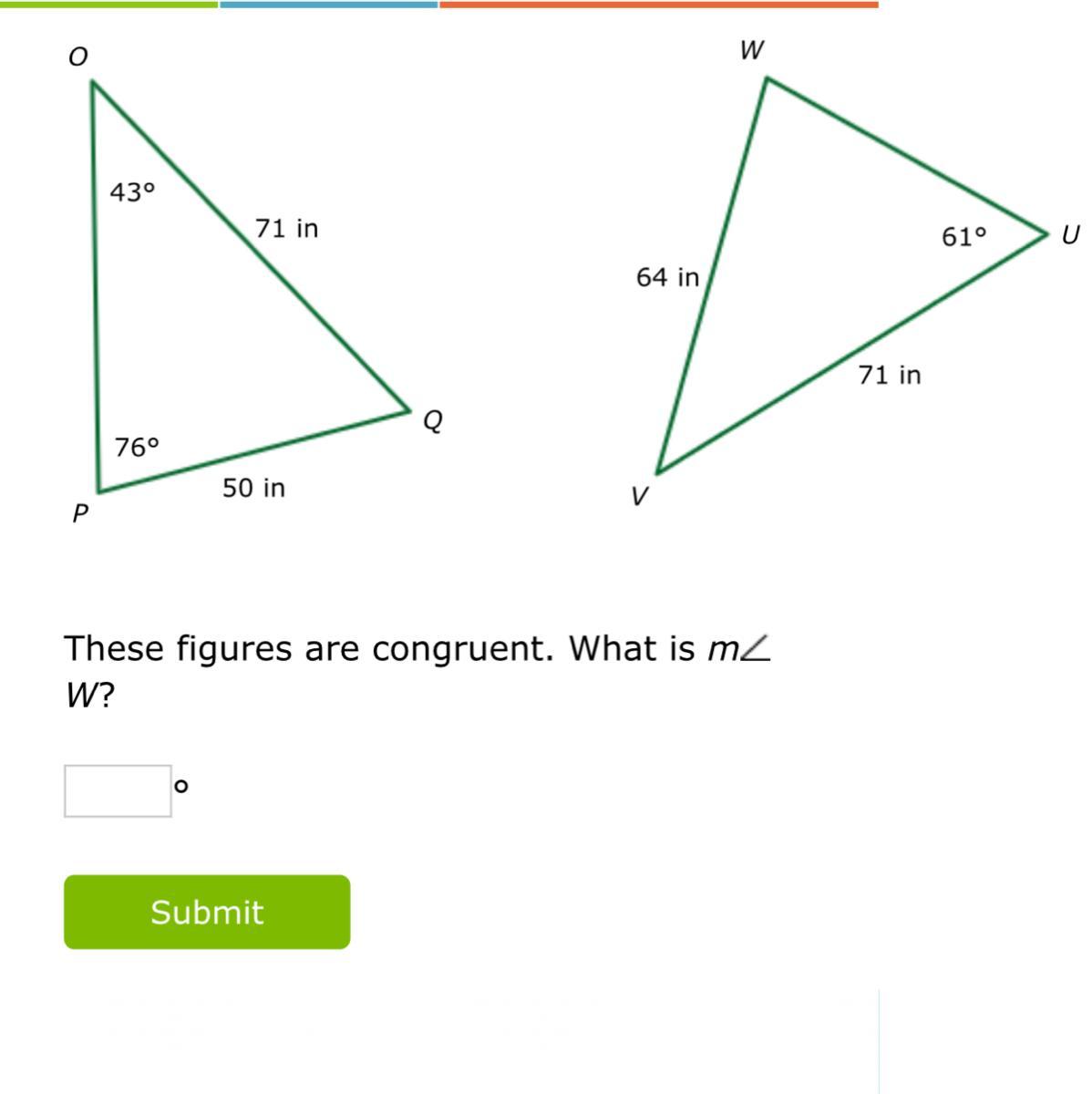
Answers
Answer:
76
Step-by-step explanation:
to check if add all angles and see if they add to 180,
then find the sides that are congruent
Xy and bd are parallel lines. x is a point ab and c is a point on bd. xb = xc
Answers
a multiple choice test consists of 160 questions with possible answers of a, b, c, and d. estimate the probability that, with random guessing, the number of correct answers is between 45 and 50, inclusive. use a ti-83, ti-83 plus, or ti-84 calculator to find the probability. round your answer to four decimal places. provide your answer below:
Answers
The estimated probability is 0.0294
How likely is it to have between 45 and 50 correct answers on a multiple-choice test with 160 questions when guessing randomly?To estimate the probability of getting between 45 and 50 correct answers on the multiple-choice test, we can use the binomial probability formula and a calculator.
The binomial probability formula is given by P(X = k) = (nCk) * p^k * q^(n-k), where n is the number of trials, k is the number of successes, p is the probability of success on a single trial.
q is the probability of failure (1 - p), and nCk represents the number of combinations.
In this case, n = 160 (number of questions), p = 0.25 (probability of guessing a correct answer), and we want to find P(45 ≤ X ≤ 50), which means the probability of getting between 45 and 50 correct answers.
Using a calculator such as TI-83, TI-83 Plus, or TI-84, we can calculate the individual probabilities for each value of X (45, 46, 47, 48, 49, 50) using the binomial probability formula.
Then, we sum up these probabilities to find the total probability of getting between 45 and 50 correct answers.
By performing the calculations, we find that the estimated probability is 0.0294, rounded to four decimal places.
This means that with random guessing, there is approximately a 2.94% chance of getting between 45 and 50 correct answers on the multiple-choice test.
Learn more about binomial distributions
brainly.com/question/29163389
#SPJ11
Help me plsss plssss plsssssss
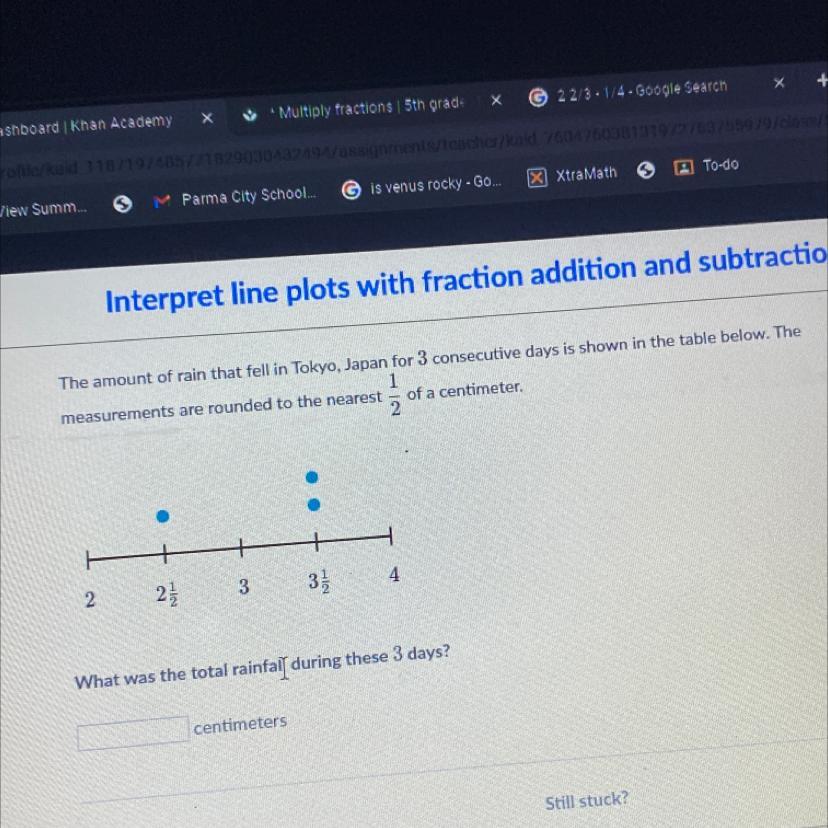
Answers
Answer:
9 1/2
Step-by-step explanation:
Add 2 1/2 plus 3 1/2 plus 3 1/2 to get 9 1/2.
Solve the initial value problem y′ 5y=t3e−5t,y(2)=0 .
Answers
To solve the initial value problem y′ 5y=t3e−5t, y(2)=0, we can use the method of integrating factors.
First, we need to identify the integrating factor, which is given by e^(∫5dt) = e^(5t).
Multiplying both sides of the differential equation by the integrating factor, we get:
e^(5t) y′ - 5e^(5t) y = t^3 e^(-t)
Using the product rule, we can rewrite the left-hand side as:
(d/dt)(e^(5t) y) = t^3 e^(-t)
Integrating both sides with respect to t, we get:
e^(5t) y = -t^3 e^(-t) - 3t^2 e^(-t) - 6t e^(-t) - 6 e^(-t) + C
where C is the constant of integration.
Using the initial condition y(2) = 0, we can solve for C:
e^(10) * 0 = -8e^(-10) + C
C = 8e^(-10)
Therefore, the solution to the initial value problem is:
y = (-t^3 - 3t^2 - 6t - 6)e^(-5t) + 8e^(-10)
and it satisfies the initial condition y(2) = 0.
To know more about initial value problem, visit:
https://brainly.com/question/30782698
#SPJ11
the number of students enrolled at a college is 15,000 and grows 4% each year
the initial amount A is ?
Answers
Answer:
15,000
Step-by-step explanation:
initial amount is basically the starting amount
what is the equation of a line when m=-7 and b=-8
Answers
(m-2)-5=8-2(m-4) ?
Answers
Answer:
m=\(\frac{23}{3}\) simplest form if you need it as a decimal its m=7.6
Step-by-step explanation:
help please i will mark brainliest

Answers
Answer:
The answer is 8.66054037 as a decimal. It's asking for a root though.
Step-by-step explanation:
of
The test scores for a group
pupils are as folows:
7, 4, 3, 9, 1,8, 4, 5, 4 what is the modal Score?
Answers
Answer:
4
Step-by-step explanation:
Modal is the most common number. There's 3 4s so 4 is the modal
HELP ME QUICK
In Shawn's class, all the students have pets. Of those pets,1/5 are cats. Of those cats, 2/3 are alley cats. What fraction of the pets are alley cats?
Answers
Answer:
2/15
Step-by-step explanation:
You want to know the fraction that is 2/3 of 1/5.
TimesIn this context, "of" means "times."
2/3 of 1/5 = (2/3)×(1/5) = (2·1)/(3·5) = 2/15
2/15 of the pets are alley cats.
Line AB passes through points A(–6, 6) and B(12, 3). If the equation of the line is written in slope-intercept form, y = mx + b, then m =–1/6 and b =____
a. -6
b. -5
c. 5
d. 6
TIMED HURRY PLS
Answers
The value of "b" is 5.
To find the value of "b" in the equation of the line y = mx + b, we need to substitute the coordinates of one of the points (A or B) and the given slope "m" into the equation and solve for "b".
Given: Point A(-6, 6), Point B(12, 3), slope m = -1/6
We can use point A(-6, 6):
y = mx + b
6 = (-1/6)(-6) + b
6 = 1 + b
b = 6 - 1
b = 5
Know more about equation here;
https://brainly.com/question/29657983
#SPJ11
Fifty eighth graders attend a
charter school. If 1/10 are
home with the flu and 2/3 of
the remaining students are
on a field trip, how many are
in school?
Answers
Answer:
15
Step-by-step explanation:
1/10 of 50 is 5, so remove that.
2/3 of 45 is 30, so remove that too.
therefore, 15 kids are in school
hope this helps!! <3
A sandwich is 5 1/2 feet long and divided into 1/2 foot pieces. How many pieces of sandwich are there?
Answers
Answer:
11
Step-by-step explanation:
Answer:
11 sandwich pieces
Step-by-step explanation:
The coach recorded the scores of nine different basketball players in their last game. ● The median number of points scored by these nine players was 13. ● The mean number of points scored by these nine players was 12. Part A: List 9 values that could represent this data set. Part B: A 10th basketball player on this team scored 12 points in the last game. If her score is added to this data set, how will the median and mean change? Explain your reasoning.
Answers
The values that could represent this data set include 5, 6, 9, 10, 12, 10, 4, 6, and 19.
How to calculate the mean?It should be noted that a mean simply means the average of a set of numbers.
In this case, the values that could represent this data set include 5, 6, 9, 10, 12, 10, 4, 6, and 19. Therefore, the mean will be:
= (5 + 6 + 9 + 10 + 12 + 4 + 6 + 19)/9
= 81/9
= 9
When a 10th basketball player on this team scored 12 points in the last game, the new mean will be:
= (81 + 12)/10
= 93/10
= 9.3
Therefore, there's an increase in mean.
Learn more about mean on:
brainly.com/question/1136789
#SPJ1
HELP I suck at algebra 1

Answers
Answer:
1. r = -4
3. n=6
5. m = -5
7. x=0.66= \(\frac{2}{3}\)
Step-by-step explanation:
1.
-52=4(7+5r)
-52=28+20r
Subtract 20r from both sides
-20r-52=28
Add 52 to both sides
-20r=80
Divide both sides by -20
r = -4
3.
8(n-5)=-5n+38
8n-40=-5n+38
Add 5n to both sides
13n-40=38
Add 40 to both sides
13n=78
Divide both sides by 13
n=6
5.
-33+5m=2(1+6m)
-33+5m=2+12m
Subtract 12m from both sides
-33-7m=2
Add 33 to both sides
-7m=35
Divide both sides by -7
m=-5
7.
2(7x-2)=2(x+4)
14x-4=2x+4
Subtract 2x from both sides
12x-4=4
Add 4 to both sides
12x=8
Divide both sides by 12
x=0.66...
True or False: If is distributed as beta with parameters and , then is Unif(, with and . Group of answer choices
Answers
False: If is distributed as a beta distribution with parameters and , then = + ( − ) is not uniformly distributed on the interval [, ].
The transformation of a beta distribution using the equation = + ( − ) does not result in a uniform distribution. Instead, follows a scaled and shifted version of the beta distribution, where the range is transformed to [, ] but the shape of the distribution remains beta-shaped.
Know more about beta distribution here:
https://brainly.com/question/32657045
#SPJ11
PleAse help me with this

Answers
Step-by-step explanation:
let this number is x
a.(x-11)/2 +7the most recent census for a city indicated that there were 909,327 residents. the population of the city is expected to increase at an annual rate of 3.6 percent each year for the next 12 years. what will the population be at that time?
Answers
Option B) 1,390,072 is correct. The population of the city after 12 years can be calculated using the formula for compound interest.
To calculate the population of a city after 12 years using the formula for compound interest, we first need to identify the initial population (P0), the annual interest rate (r), and the number of years (n). We can then plug these values into the formula P = P0(1 + r/100)ⁿ. In this case, the initial population is given as 909327, the annual interest rate is 3.6%, and the number of years is 12. By substituting these values into the formula, we get P = 909327 * (1 + 3.6/100)¹² ≈ 1390072, which represents the population of the city after 12 years. Therefore, option B) 1,390,072 is the correct answer.
Learn more about compound interest here: brainly.com/question/14295570
#SPJ4
Complete question:
The most recent census for a city indicated that there were 909,327 residents. the population of the city is expected to increase at an annual rate of 3.6 percent each year for the next 12 years. what will the population be at that time?
A) 1,491,958
B) 1,390,072
C) 1,440,114
Dan and Joe are responsible for cutting the grass on the local high school soccer field. Joe cuts a diagonal line
through the field, as shown in the diagram below, and says that each person is responsible for cutting the grass on
one side of the line. Dan says that this is not fair because he will have to cut more grass than Joe. Is Dan correct?
Why or why not?

Answers
Considering that the diagonal divided the area of the rectangle in two equal parts, Dan is not correct, as both will have to cut the same amount of grass.
What is the area of a rectangle?It is the number of square units inside of the rectangle, and for a rectangle of length l and width w it is given by:
A = lw.
The diagonal divides the area of the triangle exactly in the middle, hence Dan is not correct, as both will have to cut the same amount of grass.
More can be learned about the area of a rectangle at https://brainly.com/question/10489198
Write And equation of the parabola that has the same shape as the graph of f(x)=5x^2, but with (2,5) as the vertex
Answers
Answer:5*(x-2)^2 + 5
Step-by-step explanation:that would be the answer 5x^2-20x+25
What are the solutions of the inequality? Check the solutions. -2/5x - 9 < 9/10
Answers
We want to find the solutions for the following inequality
\(-\frac{2}{5}x-9<\frac{9}{10}\)First, we can add 9 on both sides of the inequality
\(\begin{gathered} -\frac{2}{5}x-9+9<\frac{9}{10}+9 \\ -\frac{2}{5}x<\frac{9}{10}+\frac{90}{10} \\ -\frac{2}{5}x<\frac{99}{10} \end{gathered}\)Now, we can multiply both sides by (-1). When we multiply an inequality by a negative number, it changes the sign
\(\begin{gathered} -\frac{2}{5}x\cdot(-1)<\frac{99}{10}\cdot(-1) \\ \frac{2}{5}x>-\frac{99}{10} \end{gathered}\)Multiplying both sides by 5, we have
\(\begin{gathered} \frac{2}{5}x\cdot5>-\frac{99}{10}\cdot5 \\ 2x>-\frac{99}{2} \end{gathered}\)And finally, dividing both sides by 2
\(\begin{gathered} 2x\cdot\frac{1}{2}>-\frac{99}{2}\cdot\frac{1}{2} \\ x>-\frac{99}{4} \end{gathered}\)Please help please guys I need this now
Practice and apply what you have learned:
Read the passage
"I should not have to turn the water off while I brush my teeth. First, I hate having to
brush my teeth. Plus, it's annoying to have to turn the water off when I'm brushing
my teeth. Everyone else in my family turns the water off when they brush their teeth,
so it shouldn't matter if I do or not, since I'm only one person. How much water can I
really waste?"
What is the claim?
Answers
Answer:
“I should not have to turn the water off while I brush my teeth.”
Step-by-step explanation:
A claim is a statement that expresses the main idea or position of an argument. A claim is usually supported by reasons and evidence to persuade the audience to accept it. A claim can also be challenged or refuted by counterclaims and counterarguments.
To find the claim in the passage, you need to look for the statement that expresses the author’s main idea or position on the topic of turning off the water while brushing teeth. The claim is usually found at the beginning or the end of the passage, but it can also be implied or repeated throughout. In this case, the claim is found at the beginning of the passage:
“I should not have to turn the water off while I brush my teeth.”
This is the claim because it expresses the author’s main idea or position on the topic. The rest of the passage provides reasons and evidence to support this claim, such as hating to brush teeth, finding it annoying to turn off the water, and being only one person who cannot waste much water. These reasons and evidence may not be very convincing or valid, but they still serve to support the claim.
So, the claim in the passage is I should not have to turn the water off while I brush my teeth.
if a stream drops 15 meters in 15 kilometers, what is its gradient?
Answers
The gradient of the stream is 1 meter per kilometre, which means that the stream drops 1 meter for every kilometre travelled. This is a relatively gentle slope and suggests that the stream is not flowing rapidly or eroding its bed very quickly.
The gradient of a stream is a measure of its steepness and is calculated by dividing the change in elevation by the distance travelled. In this case, the stream drops 15 meters in 15 kilometres, which means that the gradient can be calculated as follows:
Gradient = Change in elevation ÷ Distance travelled
Gradient = 15 meters ÷ 15 kilometers
Since we need to express the gradient in terms of meters per kilometre, we can simplify the above equation as follows:
Gradient = (15 meters ÷ 15,000 meters) × 1,000
Gradient = 1 meter per kilometer
Therefore, understanding the gradient of a stream is important for a range of activities, including flood control, erosion management, and habitat restoration. By monitoring changes in the gradient over time, scientists and engineers can gain insights into the health and behaviour of streams and develop strategies to protect them.
To learn more about distance travelled, refer:-
https://brainly.com/question/29055485
#SPJ11
show that if a radioactive substance has a half life of T, then the corresponding constant k in the exponential decay function is given by k= -(ln2)/T
Answers
The corresponding constant k in the exponential decay function is given by k = -(ln2)/T.
The exponential decay function for a radioactive substance can be expressed as:
N(t) = N₀\(e^{(-kt),\)
where N₀ is the initial number of radioactive atoms, N(t) is the number of radioactive atoms at time t, and k is the decay constant.
The half-life, T, of the substance is the time it takes for half of the radioactive atoms to decay. At time T, the number of radioactive atoms remaining is N₀/2.
Substituting N(t) = N₀/2 and t = T into the equation above, we get:
N₀/2 = N₀\(e^{(-kT)\)
Dividing both sides by N₀ and taking the natural logarithm of both sides, we get:
ln(1/2) = -kT
Simplifying, we get:
ln(2) = kT
Solving for k, we get:
k = ln(2)/T
for such more question on exponential decay
https://brainly.com/question/19961531
#SPJ11
The derivation of the formula k = ln2/t gives us the half life of the isotope.
What is the half life?The amount of time it takes for half of a sample's radioactive atoms to decay and change into a different element or isotope is known as the half-life. It is a distinctive quality of every radioactive substance and is unaffected by the initial concentration.
We know that;
\(N=Noe^-kt\)
Now if we are told that;
N = amount of radioactive substance at time = t
No = Initial amount of radioactive substance
k = decay constant
t = time taken
Then at the half life it follows that N = No/2 and we have that;
\(No/2 =Noe^-kt\\1/2 = e^-kt\)
ln(1/2) = -kt
-ln2 = -kt
k = ln2/t
Learn more about half life:https://brainly.com/question/31666695
#SPJ4
