Answers
it’s -0.334
then find y intercept
-6
so all together
-0.334x-6
Related Questions
[PICK ONE!]
Vocabulary How can you tell when an equation in one variable has infinitely many solutions or no solution?
When you solve for the variable, you will end up with a true statement, like 2 = 2, for an equation with no solution. You also will end up with a true statement for an equation with infinitely many solutions.
When you solve for the variable, you will end up with a false statement, like 0 = 2, for an equation with no solution. You will also end up with a false statement for an equation with infinitely many solutions.
When you solve for the variable, you will end up with a false statement, like 0 = 2, for an equation with no solution. You will end up with a true statement, like 2 = 2 for an equation with infinitely many solutions.
When you solve for the variable, you will end up with a true statement, like 2 = 2, for an equation with no solution. You will end up with a false statement, like 0 = 2 for an equation with infinitely many solutions.
Answers
Step-by-step explanation:
The answer is infinitely many solutions for both solutions.
Could someone help me with this

Answers
Answer:
first is ray
second is 5
third is 3
fourth is line
fifth is 4
Step-by-step explanation:
Line arrows on both sides
Ray dot on one side and arrow on the other side
segment dot on both sides
hope this helps!
The rabbit population in a certain area is 500% of last year's population. There are about 300 rabbits this year. How many were there last year?
Answers
Answer: 1500
Hope this helps! :)
Please mark brainliest.
Ill pay for whoever gets this right 10 dollars (if right)

Answers
Answer:
101°
Step-by-step explanation:
\(50 \degree + x \degree + (180 - 151) \degree = 180 \degree \\ \\ 50 \degree + x \degree +29 \degree = 180 \degree \\ \\ x \degree +79 \degree = 180 \degree \\ \\ x \degree = 180 \degree - 79 \degree\\ \\ x = 101 \degree\)
Another way:
x° + 50° = 151° (Alternate angles)
x° = 151° - 50°
x° = 101°
x = 101
5. Look at the two grids below How many squares can you count in each one?
Answers
You did not copy the image with the question. Sometimes you have to screenshot or use the Snip-it app to get the image.
Lavage Rapide is a Canadian company that owns and operates a large automatic car wash facility near Montreal. The following table provides estimates concerning the company’s costs:
Fixed Cost per Month Cost per Car Washed
Cleaning supplies $ 0.80
Electricity $ 1,400 $ 0.08
Maintenance $ 0.20
Wages and salaries $ 4,700 $ 0.40
Depreciation $ 8,000
Rent $ 2,100
Administrative expenses $ 1,400 $ 0.05
Answers
Lavage Rapide's total cost per car washed is $19.05.
What is equation?An equation in mathematics is a statement that states the equality of two expressions. An equation is made up of two sides that are separated by an algebraic equation (=). For example, the argument "2x + 3 = 9" asserts that the phrase "2x Plus 3" equals the value "9." The purpose of equation solving is to determine the value or values of the variable(s) that will allow the equation to be true. Equations can be simple or complicated, regular or nonlinear, and include one or more elements. The variable x is raised to the second power in the equation "x2 + 2x - 3 = 0." Lines are utilised in many different areas of mathematics, such as algebra, calculus, and geometry.
Fixed costs are expenses that do not change based on the number of units produced or sold. Variable costs, on the other hand, change with the level of production or sales. Here, the fixed costs are cleaning supplies, electricity, maintenance, wages and salaries, depreciation, rent, and administrative expenses.
The variable cost is the cost per car washed, which includes wages and salaries and administrative expenses.
To calculate the total cost per car washed, we need to add fixed costs to the variable cost per car. So, the total cost per car washed for Lavage Rapide would be:
Total Cost per Car Washed = Fixed Costs + Variable Cost per Car Washed
Total Cost per Car Washed =\(($0.80 + $1,400 + $0.20 + $4,700 + $8,000 + $2,100 + $1,400) + ($0.40 + $0.05)\)
Total Cost per Car Washed = $18,620 + $0.45
Total Cost per Car Washed = $19.05
Therefore, Lavage Rapide's total cost per car washed is $19.05.
To know more about equation visit:
brainly.com/question/649785
#SPJ1
complete question:
Fixed Cost per Month Cost per Car Washed
Cleaning supplies $ 0.80
Electricity $ 1,400 $ 0.08
Maintenance $ 0.20
Wages and salaries $ 4,700 $ 0.40
Depreciation $ 8,000
Rent $ 2,100
Administrative expenses $ 1,400 $ 0.05
Find the domain and range of the function. f(x)=24+x^2
Answers
Domain: \(x \in \mathbb{R}\)
Range: \(y \in \{ \mathbb{R} | y \geqslant 24 \}\)
Step-by-step explanation:Domain:
In finding the Domain of a function, the values for the input of the function should not make the output of the function undefined or complex. Because of this, we can think of the values for the input that make the output of the function undefined or complex so that we will not include them in our Domain. We can only make the output undefined if the input makes the denominator \(0\). In \(f(x)\), there's no value for \(x\) that makes the denominator \(0\) as it is constant, \(1\) (Note: All expressions implicitly have \(1\) as their denominator even though it's not written). We can only make the output of the function complex if the value of \(x\) makes the function take the \(n\text{th}\) root of a negative number where \(n \in \mathbb{E}\). There's no radical sign in \(f(x)\) so we shouldn't worry about the output of \(f(x)\) being complex. Because there's no value for the input, \(x\), that can make the output of \(f(x)\) undefined or complex, its Domain can be any number.
Domain: \(x \in \{\mathbb{R}\}\)
Range:
In finding the Range, it is actually the same logic as finding the Domain but first, we'll have to do a bit of rewriting for the given function.
Let \(y = f(x)\) so \(y = 24 +x^2\).
First, we need to make \(x\) the subject of the equation.
Making \(x\) the subject:
\(y = 24 +x^2 \\ y -24 = 24 +x^2 -24 \\ y -24 = x^2 \\ \pm \sqrt{y -24} = \sqrt{x^2} \\ x = \pm \sqrt{y -24}\).
In the Domain, we'll have to think of the value for the input, \(x\), that makes the output undefined or complex. In the Range, the same logic for the Domain, we'll have to think for the value of \(y\), that makes the \(x\) undefined or complex. That's why we made \(x\) in the equation the subject. In our rewritten equation, we can see that \(y -24\) is under the square root. Which means if \(y -24\) is negative, \(x\) will be complex. So we have to make \(y -24\) be greater than or equal to \(0\) (\(y -24 \geqslant 0\)) so that \(x\) won't be complex.
Solving for the inequality, \(y -24 \geqslant 0\)
\(y -24 \geqslant 0 \\ y -24 +24 \geqslant 0 +24 \\ y \geqslant 24\)
Range: \(y \in \{ \mathbb{R} | y \geqslant 24 \}\)
A university is comparing the grade point average averages of biology majors with the grade point averages of engineering majors. 25 students from each major are randomly selected. The mean and standard deviation for each sample are shown in the table.
The university wants to test if there is a significant difference in the GPAs for students in two majors. How is the appropriate test statistic calculated?
Biology Majors - (Sample Mean 3.22 , Sample Standard Deviation 0.05)
Engineering Majors - (Sample Mean 3.17 , Sample Standard Deviation 0.03).

Answers
Considering the hypothesis tested, using the t-distribution, as we have the standard deviation for the sample, it is found that the adequate test statistic is given by:
\(t = \frac{(3.22 - 3.17) - 0}{\sqrt{\frac{0.05^2 + 0.03^2}{25}}}\)
What are the hypothesis tested?At the null hypothesis, we test if there is no difference, that is, the subtraction of their means is 0, hence:
\(H_0: \mu_1 - \mu_2 = 0\)
At the alternative hypothesis, we test if there is a difference, that is, the subtraction of their means is not 0, hence:
\(H_1: \mu_1 - \mu_2 \neq 0\)
What is the distribution of the differences?For Biology Majors, we have that:
\(\mu_1 = 3.22, \sigma_1 = 0.05, n_1 = 25, s_1 = \frac{0.05}{\sqrt{25}}\)
For Engineering Majors, we have that:
\(\mu_2 = 3.17, \sigma_2 = 0.03, n_2 = 25, s_2 = \frac{0.03}{\sqrt{25}}\)
Then, for the distribution of differences, we have that:
\(\overline{x} = \mu_1 - \mu_2 = 3.22 - 3.17\)
\(s = \sqrt{s_1^2 + s_2^2} = \sqrt{\left(\frac{0.05}{\sqrt{25}}\right)^2 + \left(\frac{0.03}{\sqrt{25}}\right)^2} = \sqrt{\frac{0.05^2 + 0.03^2}{25}}\)
What is the test statistic?It is given by:
\(t = \frac{\overline{x} - \mu}{s}\)
In which \(\mu = 0\) is the value tested at the null hypothesis.
Hence:
\(t = \frac{(3.22 - 3.17) - 0}{\sqrt{\frac{0.05^2 + 0.03^2}{25}}}\)
To learn more about the t-distribution, you can take a look at https://brainly.com/question/13873630
Elroy bought a $4210 custom video gam e/ virtual sound system on a special no-interest plan. He made
Answers
The amount of the last payment that Elroy will make is $710, which includes the $200 monthly payment and a balance of $510.
How is the last payment determined?The last payment amount is the result of the mathematical operations of subtraction and multiplication.
The first mathematical operation was the subtraction of the down payment from the total cost of the video game system.
Using multiplication, the monthly payments are determined to be $3,400 for 17 months. This is subtracted from the remaining balance to obtain the last payment amount.
The cost of a custom video game/virtual sound system = $4,210
Down payment = $100
The remaining balance for monthly payment = $4,110 ($4,210 - $100)
Payment period = 18 months (1¹/₂ years)
Monthly payments = $200
Payment for the first 17 months = $3,400 (17 x 200)
Last payment = $710 ($4,110 - $3,400)
Thus, if Elroy makes the minimum monthly payment of $200 till the last payment, then he will pay $710 to settle the account.
Learn more about mathematical operations at https://brainly.com/question/20628271
#SPJ1
Question Completion:He made a $100 down payment and agreed to pay the entire purchase off in 1 1/2 years The minimum monthly payment is $200 if he makes the minimum monthly payment up until the last payment what will be the amount of his last payment?
by substituting the given values for x calculate the y value for the following equation y=x+2
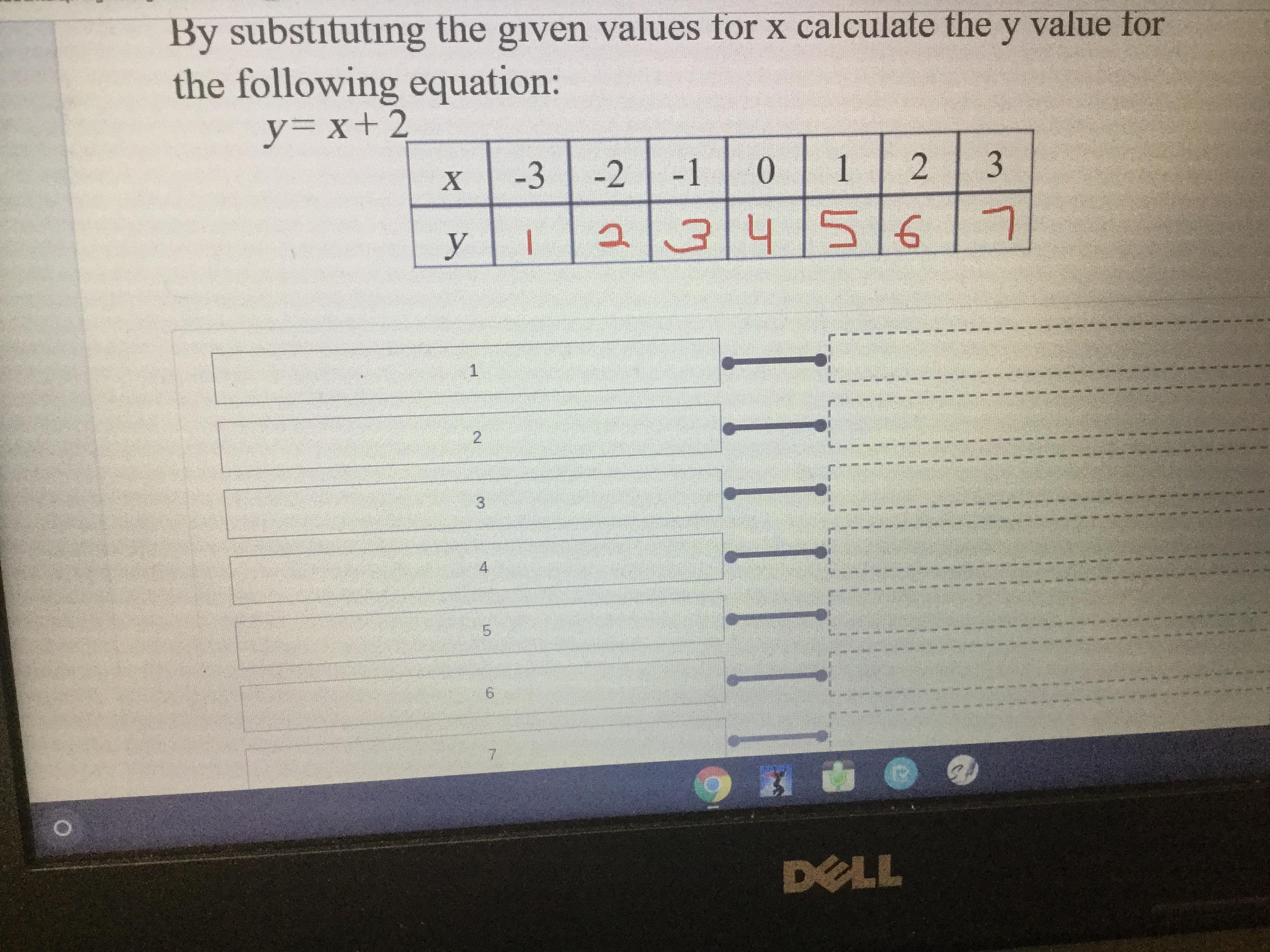
Answers
2. center (5, -6), radius 4
Answers
Answer:
(x - 5)² + (y + 6)² = 16
Step-by-step explanation:
assuming you require the equation of the circle
the equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k ) are the coordinates of the centre and r is the radius
here (h, k ) = (5, - 6 ) and r = 4 , then
(x - 5)² + (y - (- 6) )² = 4² , that is
(x - 5)² + (y + 6)² = 16
Please help. I don’t understand this math problem. I’ll mark you as brainliest if correct! Thanks

Answers
Answer:
y = (x +1)^3(x -2)
Step-by-step explanation:
The graph is generally U-shaped and opens upward. This means the polynomial is of even degree and has a positive leading coefficient.
The x-intercepts are -1 and +2, so there will be factors of (x -(-1)) and (x -2). (An x-intercept of p corresponds to a factor (x-p).)
The curve has a flat spot at x=-1, so the multiplicity of that factor will be greater than 1. Since the axis is crossed there (not just touched), the multiplicity will be odd.
The smallest exponent of the factor (x+1) that will meet all the requirements is 3. (The sum of exponents must be even, the exponent of (x+1) must be an odd number greater than 1.)
An equation could be ...
y = (x +1)^3(x -2)
_____
Comment on what's to understand?
Every x-intercept of a polynomial curve corresponds to a binomial factor with a real number constant. (Above, we called the factor (x-p) for x-intercept x=p.) If the factor has odd multiplicity, the curve will cross the x-axis; if not, the curve will "touch" the x-axis at the x-intercept point. The higher the multiplicity (exponent of the factor), the "flatter" the curve is at the x-intercept.
The leading coefficient of the polynomial tells you the sign of the y-value when x takes on large positive values. If the degree of the polynomial is even, the general shape of the curve will be U-shaped, opening upward or downward depending on the sign of the leading coefficient. If the degree of the polynomial is odd, the curve will have a / or \ general shape, again depending on the sign of the leading coefficient. (\ for negative). This description is of the shape at large scales, ignoring any wiggles on the curve.
if a is a set of real numbers which is bounded above and b is a set of real numbers which is bounded below then there is at most one real number in both a and b?
Answers
If a is a set of real numbers that is bounded above and b is a set of real numbers that is bounded below, there is at most one real number that can exist in both sets.
A real number is any number that can be expressed as a decimal or fraction and exists on the number line.
If a set of real numbers, represented by a, is bounded above, it means that there exists a real number, represented by M, such that all the numbers in the set are less than or equal to M. Similarly, if a set of real numbers, represented by b, is bounded below, it means that there exists a real number, represented by m, such that all the numbers in the set are greater than or equal to m.
Now, let's consider a real number, represented by x, that exists in both sets a and b. If x exists in a, it must be less than or equal to M and if x exists in b, it must be greater than or equal to m. Hence, x must satisfy both conditions: M >= x >= m.
From these conditions, it can be deduced that M and m must be equal to x. In other words, there can only be one real number that is simultaneously the greatest value in a and the smallest value in b.
To know more about real number here.
https://brainly.com/question/9876116
#SPJ4
The table below shows the growth of algae cells within the Chesapeake Bay. Which of the following functions models the concentration, C(d), of algae cells per milliliter in d days?
Answers
The exponential function that represent the concentration of algae cells per milliliter in d days is \(C(d) = 10(2)^d\)
What is an equation?An equation is an expression that shows the relationship between two numbers and variables.
The standard form of an exponential funtion is in the form:
y = abˣ
Where a is the initial value and b is the multiplication factor.
Let C(d) represent the concentration of algae cells per milliliter in d days
At point (1, 20)
20 = ab (1)
At point (2, 40)
40 = ab² (2)
From equations 1 and 2:
b = 2, a = 10
The exponential function that represent the concentration of algae cells per milliliter in d days is \(C(d) = 10(2)^d\)
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1

Find the missing side or angle.
Round to the nearest tenth.
C=53°
B= 80°
a=2
b=[?]
![Find the missing side or angle.Round to the nearest tenth.C=53B= 80a=2b=[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/k0pbtQdcApcIR4NTl6vx4BwP6oAvvWGt.png)
Answers
Answer:
2.69 approximately 3
Step-by-step explanation:
53⁰+80⁰+A=180⁰(sum of angles on a triangle)
133⁰+A=180
A=180-133
A=47⁰
using sine rule
2/sin 47 = b/sin 80
b sin47 = 2 sin 80
b= 1.9696/0.7314
b=2.69 approximately 3
In statistical inference for categorical data:___________.
a. Normal data is always a condition for inference.
b. Normal data is never one of the inference assumptions.
c. Normal data or large enough total sample size is one of the inference assumptions.
Answers
Answer:
b. Normal data is never one of the inference assumptions.
Step-by-step explanation:
A categorical data specifies among two or more groups, which one each observation belongs to, and one or more explanatory variables that can be used to predict this membership.
So, there are two propositions in statistical inference for categorical data
1. That each data in a cell is independent of the others.
2. That samples are randomly drawn.
Thus, there is no room for normality.
Which expression is equivalent to
ON
?
o
CUP)

Answers
Answer:
9√xy^2
Step-by-step explanation:
according to the rule of law of indices, 3√xy=xy^(1/3) like this 9√xy^2 is the correct answer
A bank requires that the Donaldson’s pay their homeowner’s insurance, property taxes,
and mortgage in one monthly payment to the bank. If their monthly mortgage payment is
$1,711.22, their annual property tax bill is $3,239, and their annual homeowner’s
insurance bill is $1880, how much do they pay the bank each month? Round to the
nearest cent.
Answers
The Donaldson's pay the bank $2,138 each month.
What is Equation?
Two or more expressions with an Equal sign is called as Equation.
we need to find the monthly property tax payment and the monthly homeowner's insurance payment.
The annual property tax bill is $3,239, so the monthly property tax payment is:
$3,239 / 12 = $269.92
The annual homeowner's insurance bill is $1,880, so the monthly homeowner's insurance payment is:
$1,880 / 12 = $156.67
Now we can add up the monthly mortgage payment, monthly property tax payment, and monthly homeowner's insurance payment:
$1,711.22 + $269.92 + $156.67 = $2,137.81
Therefore, the Donaldson's pay the bank $2,138 each month.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Complete the sentences to compare the intervals for which each function is decreasing

Answers
The intervals for which each function is decreasing are f(x) = [0, ∝) and g(x) = (-∝, ∝)
Completing the sentences to compare the intervalsFrom the question, we have the following parameters that can be used in our computation:
The functions f(x) and g(x)
From the graph of the functions, we can see that
The function g(x) decreases all through because it is a linear function with a negative slopeThe function f(x) decreases at [0, ∝) because it a quadratic function with a maximum vertex at (0, 5)Read more about functions at
https://brainly.com/question/4138300
#SPJ1
Which statements are true about the graph of y < 2x+1? Check all that apply 3 The slope of the line is 1 The line is solid The area below the line is shaded. A solution to the inequality is (2, 3) The x-intercept of the boundary line is (-2, 0) Graph y
Answers
The statements that are true about the graph of y < 2x+1 include the following:
C. The area below the line is shaded.
D. A solution to the inequality is (2, 3).
What is an inequality?In Mathematics and Geometry, an inequality simply refers to a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the inequality symbols;
Greater than (>).Less than (<).Greater than or equal to (≥).Less than or equal to (≤).Based on the information provided, we have the following equation (inequality);
y < 2x + 1
The slope of the above equation (inequality) is 2 and the y-intercept of the boundary line is (1, 0). Additionally, the area below the dashed line must be shaded because the inequality symbol is less than (<).
Read more on inequality here: brainly.com/question/27976143
#SPJ1

What are the solutions to the equation 0=|3x+3|+3
Answers
Therefore, the solutions to the equation 0 = |3x + 3| + 3 are x = -2 and x = 0.
To solve the equation 0 = |3x + 3| + 3, we need to eliminate the absolute value. Remember that the absolute value of a number is always non-negative.
First, let's isolate the absolute value term on one side of the equation:
|3x + 3| = -3
Since the absolute value cannot be negative, there are no solutions to the equation as it stands. However, if we modify the equation to make the right side positive, we can find a solution.
To eliminate the absolute value, we can rewrite the equation as two separate equations, considering both the positive and negative cases:
3x + 3 = -3
-(3x + 3) = -3
Solving equation 1:
3x + 3 = -3
3x = -6
x = -2
Solving equation 2:
-(3x + 3) = -3
-3x - 3 = -3
-3x = 0
x = 0
For such more question on equation
https://brainly.com/question/29174899
#SPJ8
(-12)^71
helppppppppppppp
Answers
Answer:
4.1866675e+76
this is the answer lol
Two athletes run a race. The first athlete starts 50 meters north of a pole and begins running towards it at 5 m/s. At the same time, the second athlete starts at the pole and begins running east at 4 m/s.
Let A (t) be the area formed by Kevin, Mary Joy, and the pole.
As a function of t, A(t)= l l
The greatest area of the triangle occurs at t= l l at which point the area
will be l l square meters.
Answers
Answer:
To find the area of the triangle formed by the two athletes and the pole at any given time t, we need to first find the position of each athlete at that time.
Let's assume that the first athlete starts at the origin (0,0) and runs towards the pole at (0,50) at a speed of 5 m/s. After time t, the first athlete will be at position (0, 5t+50).
The second athlete starts at the pole (0,50) and runs east at a speed of 4 m/s. After time t, the second athlete will be at position (4t, 50).
The area of a triangle can be calculated as half the product of its base and height. In this case, the base of the triangle is the distance between the two athletes, which can be calculated using the Pythagorean theorem:
distance = sqrt((0 - 4t)^2 + (5t)^2) = sqrt(16t^2 + 25t^2) = sqrt(41t^2)
The height of the triangle is the distance between the pole and the line connecting the two athletes. To find this distance, we need to calculate the equation of the line connecting the two athletes.
The slope of the line is (50 - 5t)/(0 - 4t) = (5t - 50)/(4t), and the y-intercept is 50. Therefore, the equation of the line is:
y = (5t - 50)/(4t) x + 50
To find the distance between the pole and the line, we need to find the perpendicular distance from the pole to the line. This can be calculated using the formula:
distance = |(ax + by + c)/sqrt(a^2 + b^2)|
where a, b, and c are the coefficients of the line equation in the form ax + by + c = 0, and x and y are the coordinates of the pole.
In this case, a = (5t - 50)/(4t), b = -1, c = 50. Plugging these values into the formula, we get:
distance = |(5t - 50)/(4t) * 0 - 1 * 50 + 50| / sqrt((5t - 50)/(4t)^2 + 1^2)
= 50 / sqrt(25/16 + 1)
= 50 / sqrt(41)
Therefore, the area of the triangle at time t is:
A(t) = 1/2 * sqrt(41t^2) * 50 / sqrt(41)
= 25t
To find the greatest area of the triangle, we need to find the value of t that maximizes the function A(t). Taking the derivative of A(t) with respect to t, we get:
dA/dt = 25
This derivative is a constant, which means that A(t) is a linear function of t and has no maximum or minimum values. Therefore, the greatest area of the triangle is infinite and occurs for any value of t.
Evaluate the integral using integration by parts with the indicated choices of u and dv. (Use C for the constant of integration.) xe7x dx; u
Answers
Answer:
\(\displaystyle \int {xe^{7x}} \, dx = \frac{e^{7x}}{7} \bigg( x - \frac{1}{7} \bigg) + C\)
General Formulas and Concepts:
Calculus
Differentiation
DerivativesDerivative NotationDerivative Property [Multiplied Constant]: \(\displaystyle \frac{d}{dx} [cf(x)] = c \cdot f'(x)\)
Basic Power Rule:
f(x) = cxⁿf’(x) = c·nxⁿ⁻¹Integration
IntegralsIntegration Property [Multiplied Constant]: \(\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx\)
U-Substitution
Integration by Parts: \(\displaystyle \int {u} \, dv = uv - \int {v} \, du\)
[IBP] LIPET: Logs, inverses, Polynomials, Exponentials, TrigStep-by-step explanation:
Step 1: Define
Identify
\(\displaystyle \int {xe^{7x}} \, dx\)
Step 2: Integrate Pt. 1
Identify variables for integration by parts using LIPET.
Set u: \(\displaystyle u = x\)[u] Basic Power Rule: \(\displaystyle du = dx\)Set dv: \(\displaystyle dv = e^{7x} \ dx\)[dv] Exponential Integration [U-Substitution]: \(\displaystyle v = \frac{e^{7x}}{7}\)Step 3: integrate Pt. 2
[Integral] Integration by Parts: \(\displaystyle \int {xe^{7x}} \, dx = \frac{xe^{7x}}{7} - \int {\frac{e^{7x}}{7}} \, dx\)[Integral] Rewrite [Integration Property - Multiplied Constant]: \(\displaystyle \int {xe^{7x}} \, dx = \frac{xe^{7x}}{7} - \frac{1}{7} \int {e^{7x}} \, dx\)Step 4: Integrate Pt. 3
Identify variables for u-substitution.
Set u: \(\displaystyle u = 7x\)[u] Basic Power Rule [Derivative Property - Multiplied Constant]: \(\displaystyle du = 7 \ dx\)Step 5: Integrate Pt. 4
[Integral] Rewrite [Integration Property - Multiplied Constant]: \(\displaystyle \int {xe^{7x}} \, dx = \frac{xe^{7x}}{7} - \frac{1}{49} \int {7e^{7x}} \, dx\)[Integral] U-Substitution: \(\displaystyle \int {xe^{7x}} \, dx = \frac{xe^{7x}}{7} - \frac{1}{49} \int {e^u} \, dx\)[Integral] Exponential Integration: \(\displaystyle \int {xe^{7x}} \, dx = \frac{xe^{7x}}{7} - \frac{e^u}{49} + C\)[u] Back-Substitute: \(\displaystyle \int {xe^{7x}} \, dx = \frac{xe^{7x}}{7} - \frac{e^{7x}}{49} + C\)Factor: \(\displaystyle \int {xe^{7x}} \, dx = \frac{e^{7x}}{7} \bigg( x - \frac{1}{7} \bigg) + C\)Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
If a die is rolled one time, find the probability of getting a six.
P(6) = ?
Answers
Answer: \(\;\;\frac{1}{6} , \;\; 0.16667,\;\; \text{or about}\;\;17\%\)
Step-by-step explanation:
A regular dice has 6 sides, and only one of those sides side has a six.
We write probability as;
\(\displaystyle \frac{\text{wanted outcomes}}{\text{possible outcomes}} = \frac{\text{number of times six is on the dice}}{\text{number of numberss on the dice}} =\frac{1}{6}\)
Hi, there!
_______
\(\boxed{\boxed{\sf{Probability=\dfrac{Favorable \ Outcomes}{Total \ Outcomes}}}}\)
Here,
» Favourable Outcome(s) -> getting a 6 on a die (1 outcome), because only one side of a die has a six on it
» Total Outcomes -> 6 (you can only get 1, 2, 3, 4, 5, 6 if you roll one die)
So,
\(\sf{Probability_{(6)}=\dfrac{1}{6}}\)
Hope the answer - and explanation - made sense to you,
happy studying!!
\(\tiny\textit{frozen \ melody}\)
Point A is located at (1, 2). Point B is located at (4, 6). Use this information to determine the length of the line, rounded to the nearest whole number.
Answers
If Point A is located at (1, 2) and Point B is located at (4, 6), the length of the line between points A and B is 5 units.
To determine the length of the line between points A and B, we can use the distance formula, which is a formula used to calculate the distance between two points in a coordinate plane. The distance formula is:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points and d is the distance between them.
Using the coordinates of points A and B, we can substitute their values into the distance formula to find the length of the line between them:
d = √((4 - 1)² + (6 - 2)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
Rounded to the nearest whole number, the length of the line is also 5 units.
In conclusion, we can use the distance formula to find the length of the line between two points in a coordinate plane. The distance formula uses the coordinates of the two points to calculate the distance between them. The resulting distance can be rounded to the nearest whole number, if needed.
To learn more about distance click on,
https://brainly.com/question/28658621
#SPJ1
Is the following relation a function?
O Yes
O No

Answers
Solve for the missing variable. Round to the nearest tenth.

Answers
Answer:
x = 4y ≈ 10.8Step-by-step explanation:
In this geometry, the triangles are similar. That means corresponding sides are proportional:
short side/long side = x/10 = 10/25
x = 100/25 = 4 . . . . multiply by 10
__
hypotenuse/short side = y/x = (x+25)/y
y² = 4(29) = 116 . . . . . use 4 for x; cross multiply
y = √116 ≈ 10.8
on certain hot summers day , 527 people used the public swimming pool. the daily prices are 1.75 for children and 2.50 for adults. the receipt for admission totaled 1054.25. how many children and how many adults swam at the public pool that day?
Answers
Explanation:
• x: number of ,children, that swam at the public pool
,• y: number of ,adults, that swam at the public pool
We can write a system of linear equations:
\(\begin{cases}x+y=527 \\ 1.75x+2.5y=1054.25\end{cases}\)Using the substitution method we can clear y from the first equation:
\(\begin{gathered} x+y=527 \\ y=527-x \end{gathered}\)Replace into the second equation:
\(\begin{gathered} 1.75x+2.5(527-x)=1054.25 \\ 1.75x+2.5\cdot527-2.5x=1054.25 \\ (1.75-2.5)x+1317.5=1054.25 \end{gathered}\)And solving for x:
\(\begin{gathered} -0.75x=1054.25-1317.5 \\ -0.75x=-263.25 \\ x=\frac{-263.25}{-0.75}=351 \end{gathered}\)Replacing x = 351 in the first equation we can find y:
\(y=527-x=527-351=176\)Answer:
• Children: ,351
,• Adults: ,176
Y=-2x-4 y=1/2x +6 what is the solution of the system of equation
Answers
Answer:
Step-by-step explanation:

Step by step
y = -2x -4 ➡️equation 1
y= 1/2x + 6 ➡️equation 2
Using substitution method, substitute the value of y from equation 1 in for y in equation 2 and solve for x
-2x -4 = 1/2x + 6
Subtract 1/2x from both sides to combine x
-2x -1/2x -4 = 1/2x - 1/2x + 6
Simplify
-2 1/2x -4 = 6
Add 4 to both sides to combine constants
-2 1/2x -4 +4 = 6 + 4
Simplify
-2 1/2x = 10
Divide both sides by -2 1/2 to solve for x
-2 1/2 / -2 1/2 x = 10 / -2 1/2
x = -4
Now substitute -4 for x in the first equation
y = -2(-4) -4
y = 8 - 4
y = 4
So your solution is ( -4, 4)
