Please help me I WILL GIVE BRAINLY IF CORRECT!!<3 Question 2(Multiple Choice Worth 2 points)
(Factoring Algebraic Expressions LC)
Rewrite 30 - 6x³ using a common factor.
O2(15-3x³)
O 2x(15-3x²)
O6(5-6x³)
O6x(5-x²)
Answers
By factorizing algebraic expression 30 - \(6x^3\) using a common factor, the result will be option (A) 2(15 - \(3x^3\))
The expression is given,
30 - \(6x^3\)
The expression is the mathematical sentence that consist of different types of variables, numbers and the mathematical operators. The mathematical operators will be addition, subtraction, division and multiplication. The expression does not contains a equal sign or inequality signs
The expression is given,
30 - \(6x^3\)
Take a common term outside
Here the common term is 2
30 - \(6x^3\) = 2((30/2) - \(6x^3\) /2)
= 2(15 - \(3x^3\))
Hence, by factorizing algebraic expression 30 - \(6x^3\) using a common factor, the result will be option (A) 2(15 - \(3x^3\))
Learn more about factorizing here
brainly.com/question/26923098
#SPJ1
Related Questions
Explain how to solve \(3^x^-^4=6\) using the change of base formula log base b of y equals log y over log b Include the solution for x in your answer. Round your answer to the nearest thousandth.
Answers
The solution of x in the equation 3^(x -4) = 6 is x = 5.63
How to determine the solution of the equation?The equation is given as
3^(x -4) = 6
Apply the law of indices on the expression 3^(x -4) to rewrite it
So, we have
3^x/3^4 = 6
The above equation becomes
3^x = 6 * 3^4
Evaluate the product
So, we have
3^x = 486
Take the logarithm of bot sides
xlog(3) = log(486)
Divide both sides by log(3)
x = log(486)/log(3)
Evaluate
x = 5.63
Hence, the solution of x in the equation 3^(x -4) = 6 is x = 5.63
Read more about equations at
https://brainly.com/question/2972832
#SPJ1
Fill The Blank ?a function is a rule that assigns to each value of the_____
Answers
In essence, a function is a rule that assigns to each value of the input set (also known as the domain), a unique value of the output set (also known as the range).
A function is a fundamental mathematical concept that is used to describe the relationship between two sets of values.
To understand the idea of a function, imagine a machine that takes in an input and produces an output. The input values are the domain of the function, and the output values are the range. A function can be represented as an equation, a graph, or a table. For example, the equation f(x) = x + 3 represents a function that takes in an input value x and produces an output value that is 3 greater than the input value.
One of the key features of a function is that each input value must have a unique output value. This means that if you input the same value into the function twice, you should get the same output value both times. In mathematical terms, we say that a function is well-defined if it has a unique output value for each input value.
Functions are used in a wide range of mathematical applications, from algebra and calculus to statistics and data analysis. They provide a powerful tool for describing and analyzing relationships between different sets of values.
To know more about function here
https://brainly.com/question/28193995
#SPJ4
I’m having problems solving this problem

Answers
D is also 55, so in the triangle there is 2 angles that are 55
To know DEF 180-55-55= 70
A phone company offers two monthly charge plans. In Plan A, there is no monthly fee, but the customer pays 9 cents per minute of use. In Plan B, the customer pays a monthly fee of $2.90 and then an additional 8 cents per minute of use. For what amounts of monthly phone use will Plan A cost more than Plan B? Use m for the number of minutes of phone use in a month, and solve your inequality for m.
Answers
A phone company offers two monthly charge plans. In Plan A, there is no monthly fee, but the customer pays 9 cents per minute of use. In Plan B, the customer pays a monthly fee of $2.90 and then an additional 8 cents per minute of use. The answer is that for m > 10,000, Plan A will cost more than Plan B.
Given: A phone company offers two monthly charge plans. In Plan A, there is no monthly fee, but the customer pays 9 cents per minute of use.
In Plan B, the customer pays a monthly fee of $2.90 and then an additional 8 cents per minute of use. To find: The amounts of monthly phone use will Plan A cost more than Plan B. Solution: We are given two plans for phone usage. A) Plan A:
There is no monthly fee, but the customer pays 9 cents per minute of use. B) Plan B: The customer pays a monthly fee of $2.90 and then an additional 8 cents per minute of use. Let m be the number of minutes of phone use in a month.(i) For Plan A, the total cost for using m minutes in a month = 0 + 0.09m = 0.09m.
(ii) For Plan B, the total cost for using m minutes in a month = 2.9 + 0.08m = 0.08m + 2.9.Now, we need to find for which values of m, Plan A is costlier than Plan B .i.e. 0.09m > 0.08m + 2.9 (As soon as plan A is more expensive than plan B we have to stop).0.01m > 2.9m > 290m > 10000So, if the number of minutes of phone use in a month is more than 10,000 minutes, then Plan A will cost more than Plan B.
Hence, we can say that if m > 10000, then Plan A will cost more than Plan B. Therefore, the answer is that for m > 10,000, Plan A will cost more than Plan B.
Note: When the inequality is solved, we get m > 10,000 which means that if the number of minutes is greater than 10,000 then Plan A will cost more than Plan B.
For more such questions on phone company
https://brainly.com/question/11716273
#SPJ8
same has 4 times as many nickels as dimes. he had 0.90 in all. how many coins of each type does he have>
Answers
The number of dimes are 2 and number of nickels are 8 according to the sum and number of coins.
Let the number of dimes be x. The number of nickels will be 4x. Also, as per the known fact, the value of dimes is 0.1 and value of nickels is 0.05. Keeping the values in formula -
0.05x + 0.1×4x = 0.90
0.05x + 0.4x = 0.90
Performing addition on Left Hand Side of the equation
0.45x = 0.9
Rewriting the equation
x = 0.9/0.45
Performing division on Right Hand Side of the equation
x = 2
Number of dimes = 2
Number of nickels = 4×2
Performing multiplication
Number of nickels = 8
Thus, there 2 dimes and 8 nickles.
Learn more about coins -
https://brainly.com/question/24342899
#SPJ4
Find the particular solution of the differential equation that satisfies the initial condition(s). f?''(x) = sin(x), f?'(0) = 2, f(0) = 3f(x)=
Answers
The particular solution of the differential equation f''(x) = sin(x) that satisfies the initial conditions f'(0) = 2, f(0) = 3 is : f(x) = -sin(x) + 3x + 3
To find the particular solution of the given differential equation, we first integrate both sides with respect to x:
f'(x) = ∫sin(x) dx = -cos(x) + C1
where C1 is the constant of integration.
Next, we integrate f'(x) again:
f(x) = ∫(-cos(x) + C1) dx = -sin(x) + C1x + C2
where C2 is the constant of integration.
To find the values of C1 and C2, we use the initial conditions:
f'(0) = -cos(0) + C1 = 2
C1 = 2 + cos(0) (Since, cos (0) = 1)
C1 = 2+1 = 3
f(0) = -sin(0) + C1(0) + C2
C2 = 0 + 0 + 3 (Since,sin(0) = 0 )
C2 = 3
Therefore, the particular solution of the differential equation that satisfies the initial conditions is:
f(x) = -sin(x) + 3x + 3
To learn more about differential equation : https://brainly.com/question/1164377
#SPJ11
Factor the expression completely. 25 a 2 − 30 a + 9 ( 5 a − 3 ) 2 ( 5 a + 3 ) 2 ( 5 a + 3 ) ( 5 a − 3 )
Answers
The factored form of the expression 25a² - 30a + 9 is (5a - 3)².
What is the factored form of the given expression?Given the expression in the question;
25a² - 30a + 9
To factor completely, first rewrite the expression as as follows;
25a² - 30a + 9
rewrite 25a² as ( 5a )²
( 5a )² - 30a + 9
rewrite 9 as 3²
( 5a )² - 30a + 3²
Now, check that the middle term is two times the product of the numbers being squared in the first and third term.
30a = 2 × ( 5a ) × 3
Next, rewrite the polynomial;
( 5a )² - 2 × ( 5a ) × 3 + 3²
( 5a )² - 2( 5a )3 + 3²
Factor using the perfect square trinomial rule.
a² - 2ab + b² = ( a - b )²
Here; a = 5a and b = 3
Hence, we have;
(5a - 3)²
Therefore, the factored form is (5a - 3)².
Learn more about factorisation here: brainly.com/question/20293447
#SPJ1
can someone please answer this

Answers
Answer:
its c
Step-by-step explanation:
Hope this helps :))
Quadrilateral KLMN is similar to quadrilateral WXYZ.
Which statement about these quadrilaterals must be true?

Answers
Angles NKL and ZWX are equal to each other
Minimize subject to Y₁+ 2y2+3y32 165 2+ Y3 $200 2y₁+ Y₁ + Y3 270 Y₁ 20. y2 20, Y3 20 Use the two-stage method to solve. The minimum is w= when y₁ - y₂- and y3 - w=2y₁ +5y2-3y3
Answers
The optimal solution and minimum value are:
y₁ = 20, y₂ = 20, y₃ = 35, w = 145.
To solve the given linear programming problem using the two-stage method, we need to follow these steps:
Step 1: Set up the initial simplex tableau by introducing slack variables and the artificial variable w.
The problem is stated as follows:
Minimize w
subject to
y₁ + 2y₂ + 3y₃ ≤ 165
2y₁ + y₂ + y₃ ≤ 200
2y₁ + y₂ + y₃ ≥ 270
y₁ ≥ 20
y₂ ≥ 20
y₃ ≥ 20
Introducing slack variables s₁, s₂, s₃, s₄, and s₅, we have:
y₁ + 2y₂ + 3y₃ + s₁ = 165
2y₁ + y₂ + y₃ + s₂ = 200
2y₁ + y₂ + y₃ - s₃ + s₄ = 270
-y₁ - y₂ - y₃ - s₅ = 0
Adding the artificial variable w, we get the following initial tableau:
| Basis | y₁ | y₂ | y₃ | s₁ | s₂ | s₃ | s₄ | s₅ | w | RHS |
|-------|----|----|----|----|----|----|----|----|---|-----|
| s₁ | 1 | 2 | 3 | 1 | 0 | 0 | 0 | 0 | 0 | 165 |
| s₂ | 2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 200 |
| s₃ | 2 | 1 | 1 | -1 | 0 | 1 | 1 | 0 | 0 | 270 |
| s₅ | -1 | -1 | -1 | 0 | 0 | 0 | 0 | -1 | 0 | 0 |
| w | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
Step 2: Perform the simplex method to obtain an optimal solution.
Using the simplex method, we perform row operations to pivot and update the tableau until we reach the optimal solution.
The optimal solution and minimum value are:
y₁ = 20, y₂ = 20, y₃ = 35, w = 145.
Learn more about row operations here:
https://brainly.com/question/17820168
#SPJ11
i need help with this problem. please?!?

Answers
Answer:
Step-by-step explanation:
B
Jake tossed a paper cup 50 times and recorded how it landed. the table shows the results:
position
open side up closed side up landing on side
1
5
44
number of times landed in position
based on the table, determine the experimental probability of each outcome (landing open side up, landing closed side up, and landing on its side). show your work
2
xd
c
e!
23
3
12 source vc
bius x, xi :-
29
ee
styles
normal
. ?
Answers
The experimental probability of each event is as follows:
Landing open side up = 1/50 = 0.02 = 2%.Landing closed side up = 5/50 = 1/10 = 0.1 = 10%.Landing on its side = 44/50 = 0.88 = 88%.The experimental probability of an event is the ratio of the number of outcomes that favored the event to the total number of outcomes in the experiment.
In the question, we are given that Jake tossed a paper cup 50 times and recorded the position how it landed, which is shown in the table:
Open-sided up: 1
Closed side up 5
On the side: 44.
We are asked to determine the experimental probability of each outcome.
The number of outcomes, when the landing is open-sided up is 1.
The number of outcomes, when the landing is closed-sided up is 5.
The number of outcomes, when the landing is on the side up is 44.
The total number of times the experiment took place is 50.
Thus, the experimental probability of each event is as follows:
Landing open side up = 1/50 = 0.02 = 2%.Landing closed side up = 5/50 = 1/10 = 0.1 = 10%.Landing on its side = 44/50 = 0.88 = 88%.Learn more about the experimental probability at
https://brainly.com/question/24298250
#SPJ4
A computer is programmed to generate a sequence of three digits, where each digit is either 0 or 1, and each of these is equally likely to occur. construct a sample space that shows all possible three-digit sequences of 0s and 1s and then find the probability that a sequence will contain exactly one 0. a. 000, 001, 010, 011, 100, 101, 110, 111; the probability is startfraction 7 over 8 endfraction. b. 001, 011, 101, 111; the probability is startfraction 2 over 8 endfraction. c. 000, 010, 011, 101, 111; the probability is startfraction 2 over 8 endfraction = one-fourth. d. 000, 001, 010, 011, 100, 101, 110, 111; the probability is startfraction 3 over 8 endfraction.
Answers
The probability that a sequence will contain exactly one 0 is 3/8.
What is probability?
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1,
We should consider sequences of three digits, where each digit is either 0 or 1. A sequence has three places .
where each place has two possibilities, i.e., 0 or 1, so, for the multiplication rule
we know that the sample space will have (2)(2)(2) = 8 sample points.
Specifically, the sample space is
S = {111, 110, 101, 011, 100, 010, 001, 000},
There are three sequences with exactly one 0.
Therefore the probability that a sequence will contain exactly one 0 is 3/8.
To know more about probability follow
https://brainly.com/question/24756209
Which equation represents a line through points (–8, 3) and (–2, –3)?
Answers
Answer:
y = -x - 5
Step-by-step explanation:
To find the equation of the line passing through two given points, we can use the point-slope form of a linear equation:
y - y1 = m(x - x1)
Where m is the slope of the line, and (x1, y1) are the coordinates of one of the points on the line.
We first need to find the slope of the line passing through the two given points. We can use the formula:
m = (y2 - y1)/(x2 - x1)
where (x1, y1) = (-8, 3) and (x2, y2) = (-2, -3)
m = (-3 - 3) / (-2 - (-8)) = -6 / 6 = -1
Now, we can use the point-slope form of the equation with one of the given points, say (-8, 3):
y - 3 = -1(x - (-8))
Simplifying:
y - 3 = -x - 8
y = -x - 5
Answer:
(-8, 3) and (-2, -3) is y = -x - 5
Step-by-step explanation:
To find the equation of a line passing through two given points, we can use the point-slope form of a linear equation:
y - y1 = m(x - x1)
Where (x1, y1) are the coordinates of one of the points on the line, and m is the slope of the line.
Given the points (-8, 3) and (-2, -3), we can calculate the slope (m) using the formula:
m = (y2 - y1) / (x2 - x1)
Substituting the coordinates into the formula:
m = (-3 - 3) / (-2 - (-8))
m = (-3 - 3) / (-2 + 8)
m = (-6) / (6)
m = -1
Now that we have the slope (m = -1) and one of the points (x1, y1) = (-8, 3), we can use the point-slope form to write the equation:
y - 3 = -1(x - (-8))
y - 3 = -1(x + 8)
y - 3 = -x - 8
y = -x - 8 + 3
y = -x - 5
Therefore, the equation that represents a line passing through the points (-8, 3) and (-2, -3) is y = -x - 5.
Hope this helped :)
At present the sum of Geetha's age and her daughter's age is 44 years. After 2 years, Geetha's age will be three times that of her daughter's age. Find their present ages.
Answers
Answer:
Geetha is 32.5 years old
her daughter is 11.5 years old
Step-by-step explanation:
sum of their ages is 44 years
G + D = 44
in two years, Geetha's age is 3 times her daughters age. (to find present age, subtract 2)
G = 3D - 2
substitute
(3D - 2) + D = 44
combine like terms
4D - 2 = 46
4D = 46
D = 11.5
plug in D to either equation
G + (11.5) = 44
G = 32.5
G = 3(11.5) - 2
G = 32.5
verify that the following equation is an identity. (sinx cosx)^2=sin2x 1
Answers
The equation \((sin(x)cos(x))^2 = sin(2x)\) is verified to be an identity.
Simplify LHS and RHS?
To verify whether the equation \((sin(x)cos(x))^2 = sin(2x)\) is an identity, we can simplify both sides of the equation and see if they are equivalent.
Starting with the left side of the equation:
\((sin(x)cos(x))^2 = (sin(x))^2(cos(x))^2\)
Now, we can use the trigonometric identity \(sin(2x) = 2sin(x)cos(x)\) to rewrite the right side of the equation:
\(sin(2x) = 2sin(x)cos(x)\)
Substituting this into the equation, we have:
\((sin(x))^2(cos(x))^2 = (2sin(x)cos(x))\)
Next, we can simplify the left side of the equation:
\((sin(x))^2(cos(x))^2 = (sin(x))^2(cos(x))^2\)
Since both sides of the equation are identical, we can conclude that the given equation is indeed an identity:
\((sin(x)cos(x))^2 = sin(2x)\)
Hence, the equation \((sin(x)cos(x))^2 = sin(2x)\) is verified to be an identity.
To know more about identity, refer here:
https://brainly.com/question/1412354
#SPJ4
Jim is buying some clothes at Kohls. He buys a jacket that costs $75 and 5 pairs of shorts that each cost the same amount. He spends a total of $175 on the shorts and jacket. Write and solve an equation to find the cost of each pair of shorts.
Answers
The equation to find the cost of each pair of shorts is 175 = 75 + 5x where each short cost $20
How to write and solve an equation?Cost of jackets= $75
Number of shorts= 5
Cost of each short = x
Total amount Jim spent= $175
Total amount Jim spent = Cost of jackets + (Number of shorts × Cost of each short)
175 = 75 + 5x
subtract 75 from both sides
175 - 75 = 5x
100 = 5x
divide both sides by 5
x = 100/5
x = $20
Ultimately, each pair of shorts cost $20
Read more on equation:
https://brainly.com/question/13729904
#SPJ1
One number exceeds another by 3. One third of their sum is 5 less than the smaller number. Find the numbers
Answers
Answer:
18 and 21 (I think)
Step-by-step explanation:
So, lets assume the equation is x + x + 3 is the 2 numbers (number 1 is x)
then divide by 3
You get: (2x+3)/3 = x-5
then, multiply both sides by 3:
2x+3=3x-15
Simplify:
18 = x
18 is the smaller number
21 is the bigger one. (18+3)
there are four bacteria in an egg salad that is left out at room temperature. after two hours, how many bacteria will be in the egg salad?
Answers
The number of bacteria in an egg salad that is left out at room temperature is 256 option D.
The bacteria would double 4 times in 2 hours, so the total number of bacteria in the egg salad would be 256.
So we have 4 bacteria after 2 hours we have,
4 x 4 x 4 x 4 = 256 bacteria.
Probability denotes the likelihood of something happening. It is a mathematical discipline that deals with the occurrence of a random event. The value ranges from zero to one. Probability has been introduced in mathematics to predict the likelihood of occurrences occurring.
Probability is defined as the degree to which something is likely to occur. This is the fundamental probability theory, which is also utilised in probability distribution, in which you will learn about the possible results of a random experiment. To determine the likelihood of a particular event occurring, we must first determine the total number of alternative possibilities.
Learn more about Number of bacteria:
https://brainly.com/question/17068291
#SPJ4
Complete question:
There are four bacteria in an egg salad that is left out at room temperature. After two hours, how many bacteria will be in the egg salad?
- 32
- 2048
- 8
- 256
the average starting salary for this year's graduates at a large university (lu) is $20,000 with a standard deviation of $8,000. furthermore, it is known that the starting salaries are normally distributed. a. what is the probability that a randomly selected lu graduate will have a starting salary of at least $30,400? b. individuals with starting salaries of less than $15,600 receive a low income tax break. what percentage of the graduates will receive the tax break? c. what are the minimum and the maximum starting salaries of the middle 95% of the lu graduates? d. if 189 of the recent graduates have salaries of at least $32,240, how many students graduated this year from this university?
Answers
(a) Probability that a randomly selected is 9.68%; (b) 29.12% will receive the tax break; (c) Minimum and the maximum starting salaries are 35,679.71 and 4,320.29. (d) 6.3% of the total number of students.
a) P(X>30,400) = P(Z>(30,400-20,000)/8,000)
= 1-P(Z<1.3)
= 0.0968
= 9.68%
b) P(X<15600) = P(Z<(15600-20000)/8000)
= 29.12%
c) Maximum of the starting salaries of the middle 95% is
(x - 20,000)/8,000 = 1,96
x = 35,679.71
Minimum of the starting salaries of the middle 95% is
(x - 20,000)/8,000 = -1,96
x = 4,320.29
d) P(X>32,240) = 1-P(Z<(32,240-20,000)/8,000)
= 0.063
Therefore, the 189 represents 6.3% of the total number of students, means that the total number is 3,000.
To know more about Probability:
brainly.com/question/13604758
#SPJ4
an equilateral triangle has a side measure of 10 in. what is the measure of each of the angles of the triangle? question 1 options: 10 degrees 60 degrees 30 degrees 18 degrees
Answers
On solving the provided question, we can say that since an equilateral triangle so, each angle will be 60
What is triangle?A triangle is a polygon since it has three sides and three vertices. It is one of the basic geometric shapes. The name given to a triangle containing the vertices A, B, and C is Triangle ABC. A unique plane and triangle in Euclidean geometry are discovered when the three points are not collinear. Three sides and three corners define a triangle as a polygon. The triangle's corners are defined as the locations where the three sides converge. 180 degrees is the result of multiplying three triangle angles.
since an equilateral triangle has a side measure of 10 in.
and it is a equilateral triangle
so, all sides will be 10
so, each angle will be 60
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ4
What is the greatest common factor of 49, 62 and 80?
Answers
Answer:
literally 1
Step-by-step explanation:
scooby ate my scooby snax
Answer:
Your answer is...
1.Step-by-step explanation:
To find the greatest common factor, you have to list the prime factors of each number. That is how you find any GCF.
Plsss guys I have it due tomorrow? Plss helpp
What's the steepest ladder you would personally be willing to climb?the shallowest?
Answers
Answer:
The steepest ladder I personally would climb: TWO STORIES
The steepest ladder I personally would climb: UP TO THE ATTIC
Explanation:
The steepest ladder I would be willing to climb, personally, is one that leads up 2 stories. 2 stories only. I am scared of heights so I don't do climbing very well. If it is an emergency then I will climb that I have to but I think that without an emergency my limit would be 2 STORIES. And there better be firefighters.
The shallowest ladder I would be willing to climb is maybe one going to the ceiling or maybe even a slide (when I was younger at least). This is because if a ladder goes higher than an attic, I don't want anything to do with it. If it is any lower, what is the point of climbing it? Where am I trying to get to? Also if the ladder is too low the ground, I am practically crawling on a nearly horizontal ladder. There is no point.
Andrea is conducting an experiment rolling a pair of number cubes, numbered from 1 through 6. She will roll the number cubes 36 times to test the prediction of a 1 out of 6 chance of rolling matching numbers; that is, both cubes show the same number. If her experiment holds true to the prediction, how many of the 36 times would matching numbers appear?

Answers
Answer:
6 times
Step-by-step explanation:
\( \frac{1}{6} \times 36 = 6\)
f(x)={10 for 0≤x≤1 elsewhere a. Select the probability density function. b. What is the probability of generating a random number between 0.25 and 0.75 (to 1 decimal place)? c. What is the probability of generating a random number with a value less than or equal to 0.3 (to 1 decimal place)? d. What is the probability of generating a random number with a value greater than 0.7 (to 1 decimal place)? e. Using 50 random numbers given below, compute the mean and standard deviation.
Answers
a. The probability density function is f(x) = 1 for 0 ≤ x ≤ 1 and f(x) = 0 elsewhere. b. The probability of generating a random number between 0.25 and 0.75 is 0.5 (50%). c. The probability of generating a random number ≤ 0.3 is 0.3 (30%). d. The probability of generating a random number > 0.7 is 0.3 (30%).
To determine the probability density function (pdf) for the given function, we need to calculate the integral of the function over its entire domain and normalize it so that the total area under the curve is equal to 1.
a. Probability Density Function (pdf):
For 0 ≤ x ≤ 1, f(x) = 10, and elsewhere, f(x) = 0.
To find the pdf, we need to calculate the integral of f(x) over its domain [0, 1]:
∫[0,1] f(x) dx = ∫[0,1] 10 dx = 10x ∣[0,1] = 10(1) - 10(0) = 10
To normalize the pdf, we divide each value by the total area:
f(x) = 10/10 = 1 for 0 ≤ x ≤ 1
f(x) = 0 elsewhere
Therefore, the pdf is:
f(x) = 1 for 0 ≤ x ≤ 1
f(x) = 0 elsewhere
b. Probability of generating a random number between 0.25 and 0.75:
To calculate the probability of generating a random number between 0.25 and 0.75, we need to calculate the integral of the pdf over this range and normalize it:
P(0.25 ≤ x ≤ 0.75) = ∫[0.25,0.75] f(x) dx
Since the pdf is constant (equal to 1) over this range, the probability is simply the width of the range:
P(0.25 ≤ x ≤ 0.75) = 0.75 - 0.25 = 0.5
Therefore, the probability of generating a random number between 0.25 and 0.75 is 0.5 (or 50%).
c. Probability of generating a random number ≤ 0.3:
To calculate the probability of generating a random number with a value less than or equal to 0.3, we need to calculate the integral of the pdf over the range [0, 0.3]:
P(x ≤ 0.3) = ∫[0,0.3] f(x) dx = ∫[0,0.3] 1 dx = x ∣[0,0.3] = 0.3 - 0 = 0.3
Therefore, the probability of generating a random number ≤ 0.3 is 0.3 (or 30%).
d. Probability of generating a random number > 0.7:
To calculate the probability of generating a random number with a value greater than 0.7, we need to calculate the integral of the pdf over the range (0.7, 1]:
P(x > 0.7) = ∫[0.7,1] f(x) dx = ∫[0.7,1] 1 dx = x ∣[0.7,1] = 1 - 0.7 = 0.3
Therefore, the probability of generating a random number > 0.7 is 0.3 (or 30%).
To know more about Probability:
brainly.com/question/32117953
#SPJ4
--The given question is incomplete, the complete question is given below " f(x)={10 for 0≤x≤1 elsewhere a. Select the probability density function. b. What is the probability of generating a random number between 0.25 and 0.75 (to 1 decimal place)? c. What is the probability of generating a random number with a value less than or equal to 0.3 (to 1 decimal place)? d. What is the probability of generating a random number with a value greater than 0.7 (to 1 decimal place)? "--
A veterinarian knows that a 50-pound dog gets 0.5 milligram of a certain medicine, and that the number of milligrams, m, varies directly with the weight of the dog, w. The vet uses these steps to find the amount of medicine to give a 10-pound dog. Step 1 Find the constant of variation. Step 2 Write the direct variation equation. Step 3 Substitute 10 into the equation to find the dosage for a 10-pound dog. Step 4 Solve for w. The 10-pound dog needs 1000 milligrams. In which step did the veterinarian make the first error? Step 1 Step 2 Step 3 Step 4
Answers
1. Divide the amount needed by the weight:
0.5 milligram / 50 pounds = 0.01 milligram per pound.
2. m = 0.01w
3. m = 0.01(10)
4 m = 0.01 x 10
0.1 milligrams
The error was step 1.
Answer:
Step 3
Step-by-step explanation:
They put the 10 in the wrong place.
In looking at an online store, I see some pants that I like. The pants come in 5 colors, 8 sizes, and 3 styles. In all, there are _____ different pants.
Answers
There are 120 different pants available in the online store.
To determine the total number of different pants, we need to multiply the number of options for each attribute: color, size, and style.
Number of colors = 5
Number of sizes = 8
Number of styles = 3
Total number of different pants = Number of colors × Number of sizes × Number of styles
= 5 × 8 × 3
= 120
Therefore, there are 120 different pants available in the online store.
To learn more on Combinations click:
https://brainly.com/question/19692242
#SPJ4
PLS ANSWER!! 30 points!

Answers
Answer:
2nd one
Step-by-step explanation:
multiply 2 and 4 to get 8
multiply -6 and 1 to get -6
Answer:
The last option as well as the second one
Step-by-step explanation:
2(-6)= -12
4(1)=4
8(-6)= -48
The diameter of a rain barrel is 1.2 meters and the surface area is 9.0432 square meters, what is height, in meters, of the barrel? Round your answer to the nearest tenth. Use 3.14 for pi
Answers
The height of the barrel with the given surface area is 1.8 meters.
What is surface area?The whole area that a three-dimensional object's surface takes up is referred to as surface area. It is the total of the areas of all the object's faces or surfaces. Depending on the measurement unit for the object's size, surface area is expressed in square units such as square inches (in2) or square metres (m2). Surface area is a crucial geometrical notion with several practical applications in the fields of construction, architecture, and engineering.
The surface area of the cylinder is given as:
A = 2πr² + 2πrh
Now, substituting the value of the surface area and r = 1.2 /2 = 0.6 we have:
9.0432 = 2(3.14)(0.6)² + 2(3.14)(0.6)h
9.0432 = 2.256 + 3.768h
6.7872 = 3.768h
h = 1.8 meters
Hence, the height of the barrel with the given surface area id 1.8 meters.
Learn more about surface area here:
https://brainly.com/question/29101132
#SPJ1
WILL GIVE BRAINLIEST + THANKS !
‘question’ 1 options: yes / no
‘question’ 2 options:
p= 5,184a
or
a = 5,184p
or
p= 0.0001929a
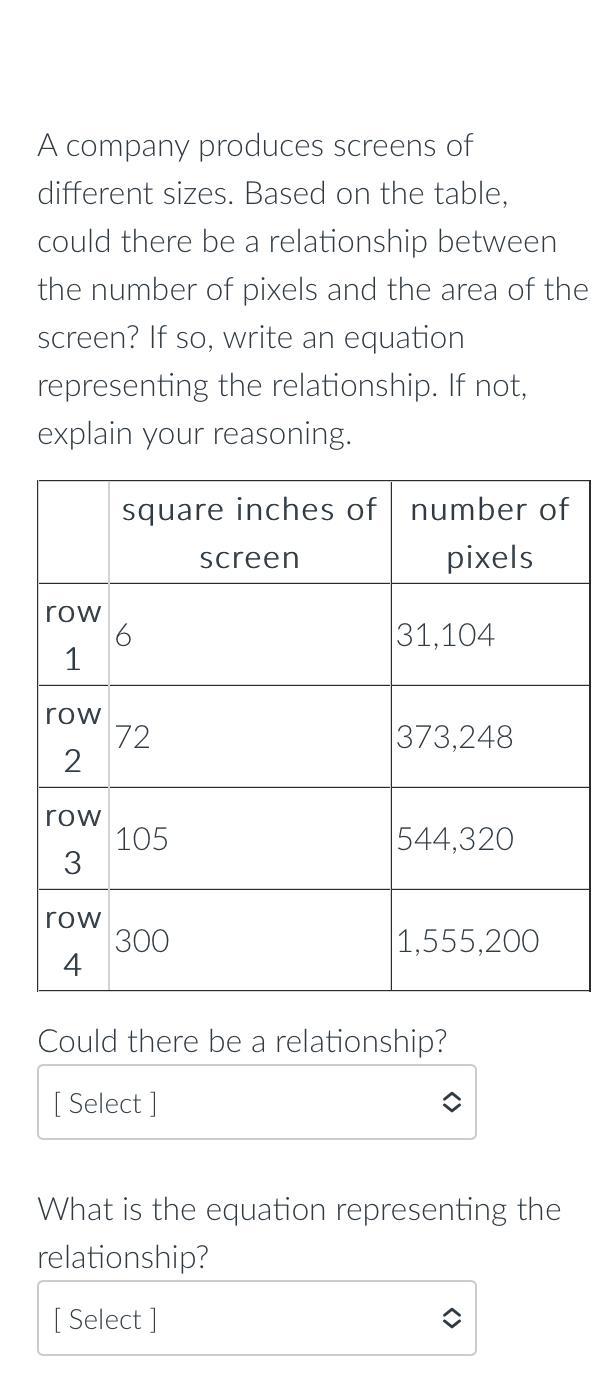
Answers
Yes, there is a relationship between the screen size and the number of pixels.
The equation representing the relationship will be a = 5,184p.
How to illustrate the information?It should be noted that the information is to simply know if there is a relationship between the screen size and the number of pixels.
The equation representing the relationship will be:
= Number of pixels / Screen size
= 31.104 / 6
= 5.184
Therefore, the equation representing the relationship will be a = 5,184p.
Learn more about numbers on:
brainly.com/question/25710806
#SPJ1