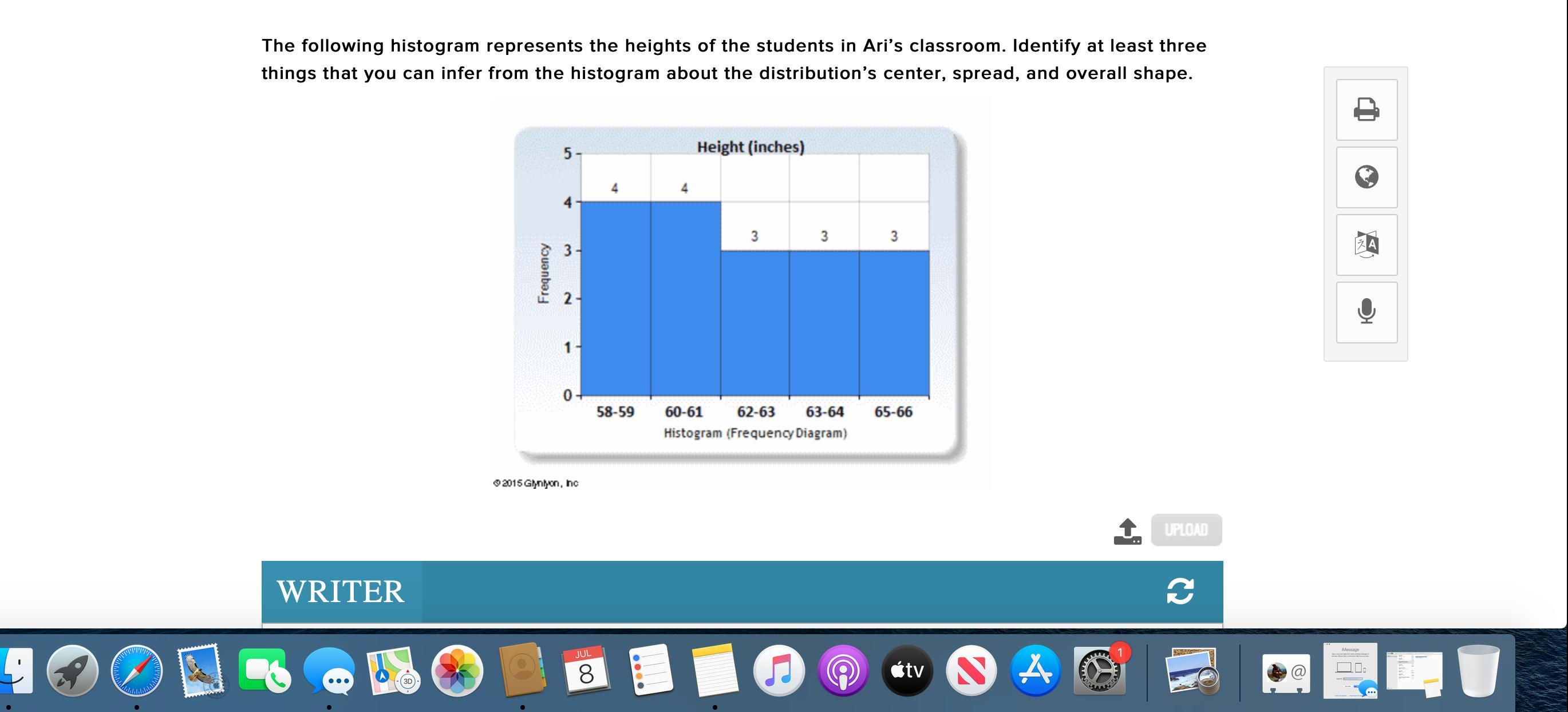
Answers
This histogram is skewed to the left and its distribution's center would be three (3).
What is a histogram?A histogram is used to graphically represent a set of data points into user-specified ranges, especially through the use of rectangular bars.
In this scenario, we can infer the following about the histogram distribution's center, spread, and overall shape:
This histogram is skewed to the left.Its distribution's center would be three (3). The spread implies that more students are between 58-59 and 60-61 inches.The shape shows that many of the values are at the lower end.Read more on histogram here: brainly.com/question/21304143
#SPJ1
Related Questions
What is the length of a rectangle that has a width of 8 centimeters and an area of 256 square centimeters
Answers
Answer:
L = 32 cm
W = 8 cm
A = 256cm square
Step-by-step explanation:
Find the equation of the line passing
through the points (4,1) and (2, 9).
y = [ ? ]x + [ ]
Answers
The equation of the line passing through the points (4, 1) and (2, 9) is:
y = -4x + 17.
To find the equation of the line passing through the points (4, 1) and (2, 9), we can use the formula for the equation of a line:
y - y₁ = m(x - x₁),
where (x₁, y₁) represents one of the points on the line, and m represents the slope of the line.
First, let's calculate the slope (m):
m = (y₂ - y₁) / (x₂ - x₁),
where (x₂, y₂) is the other point on the line.
Using the points (4, 1) and (2, 9):
m = (9 - 1) / (2 - 4) = 8 / (-2) = -4.
Now that we have the slope (m), we can choose either of the given points and substitute its coordinates into the equation:
Using (4, 1):
y - 1 = -4(x - 4).
Expanding and simplifying:
y - 1 = -4x + 16,
y = -4x + 17.
Learn more about equation here:
https://brainly.com/question/29538993
#SPJ11
derive the slope for drinks in the simple regression from the slope for drinks in the multiple regression. in other words show how you get from:
Answers
To derive the slope for a single variable regression from the slope in a multiple regression, you can use the concept of partial derivatives.
In a multiple regression model, we have several independent variables (predictors) that are used to predict a dependent variable. Let's say we have a multiple regression model with two independent variables: X1 and X2, and a dependent variable Y. The regression equation can be written as:
Y = b0 + b1X1 + b2X2
To find the slope for the variable X1, we need to hold all other variables constant and differentiate the regression equation with respect to X1. The partial derivative of Y with respect to X1 (denoted as ∂Y/∂X1) gives us the slope for X1 in the multiple regression model.
∂Y/∂X1 = b1
Therefore, the slope for X1 in the multiple regression is simply equal to b1, the coefficient of X1 in the regression equation.
So, to derive the slope for X1 in the simple regression model, you can directly use the coefficient b1 obtained from the multiple regression analysis.
To know more about variable visit-
brainly.com/question/28461635
#SPJ11
What is the difference between a discrete
probability distribution and a continuous
probability distribution?
Give your own example of each. What is the
expected value, and what does it measure?
How is it computed for a discrete probability
distribution?
Answers
A discrete probability distribution is a statistical distribution that relates to a set of outcomes that can take on a countable number of values, whereas a continuous probability distribution is one that can take on any value within a given range.Therefore, the main difference between the two types of distributions is the type of outcomes that they apply to.
An example of a discrete probability distribution is the probability of getting a particular number when a dice is rolled. The possible outcomes are only the numbers one through six, and each outcome has an equal probability of 1/6. Another example is the probability of getting a certain number of heads when a coin is flipped several times.
On the other hand, an example of a continuous probability distribution is the distribution of heights of students in a school. Here, the range of heights is continuous, and it can take on any value within a given range.
The expected value of a probability distribution measures the central tendency or average of the distribution. In other words, it is the long-term average of the outcome that would be observed if the experiment was repeated many times.
For a discrete probability distribution, the expected value is computed by multiplying each outcome by its probability and then adding the results. In mathematical terms, this can be written as E(x) = Σ(xP(x)), where E(x) is the expected value, x is the possible outcome, and P(x) is the probability of that outcome.
For example, consider the probability distribution of the number of heads when a coin is flipped three times. The possible outcomes are 0, 1, 2, and 3 heads, with probabilities of 1/8, 3/8, 3/8, and 1/8, respectively. The expected value can be computed as E(x) = (0*1/8) + (1*3/8) + (2*3/8) + (3*1/8) = 1.5.
Therefore, the expected value of the distribution is 1.5, which means that if the experiment of flipping a coin three times is repeated many times, the long-term average number of heads observed will be 1.5.
Two plumbers received a job. At first, one of the plumbers worked alone for 1 hour, and then they worked together for the next 4 hours. After this 40% of the job was complete. How long would it take each plumber to do the whole job by himself if it is known that the first plumber would take 5 more hours to finish the job than the second plumber?
Answers
Answer: https://www.algebra.com/algebra/homework/Rate-of-work-word-problems/Rate-of-work-word-problems.faq.hide_answers.1.html
Step-by-step explanation:
here use this link above to answer your question
Clara found a nickel, a quarter, two dimes, another quarter, and two pennies in her desk drawer, how much money did clara find?
Answers
Answer:77 cents Clara found 77 cents bc you just need to add up the cents and you have it
77 cents
Step-by-step explanation:So 2 quarters is 50 cents and you have a nickel: 5 cents, then you have 2 pennies (2 cents), then you have 2 dimes. Now all you have to do is add them all together to get your answer.
5 cents + 25 cents= 30 cents
30 cents + 20 cents= 50 cents
50 cents + 25 cents= 75 cents
75 cents + 2 cents= 77 cents
So Clara would have 77 cents in her desk drawer.
an architect designs a rectangular flower garden such that the width is exactly two thirds of the length. if 230 feet of antique picket fencing are to be used to enclose the garden, find the dimensions of the garden.
Answers
Answer:
length = 69 ft. width = 46 ft.Step-by-step explanation:
perimeter (p) = 2L + 2W
where P = 230 ft.
W = 2/3L
plugin values into the formula:
230 = 2L + 2(2L/3)
230 = 2L + 4/3L
230 = 10/3L
L = 690/10
L = 69
W = 2/3L
W = (2/3) 69
W = 46
P = 2(69) + 2(46)
P = 230 ft.
therefore,
the dimensions of the rectangular garden:
length = 69 ft
width = 46 ft.
Find the exact length of the third side.
30
72
Answers
Because of the special right triangles (5, 12, 13) these give numbers are multiples so by finding the common multiple i was able to determine the final side length given it is a right triangle
WILL MARK AS BRAINLEIST!! ASAP PLEASE!!
Question in picture
I have more questions on my account if u can help me out!!

Answers
For the region above x + 3y = 9 and below x + 9 = y², we have:
a = 18, b = -9, f(x) = (y² - 9)/3, and g(x) = (9 - x)/3.
For single integration: α = -6, β = 3 and h(y) = [(9 - y²)/3 - (y² - 9)].
What is the area bounded by the curves?To solve this problem, we first need to find the intersection points of the two curves x + 3y = 9 and x + 9 = y². We can do this by solving the system of equations:
x + 3y = 9
x + 9 = y²
Rearranging the first equation, we get:
x = 9 - 3y
Substituting this expression for x into the second equation, we get:
9 - 3y + 9 = y²
Simplifying, we get:
y² - 3y - 18 = 0
Factorizing, we get:
(y - 6)(y + 3) = 0
So the solutions are:
y = 6 or y = -3
Substituting these values of y into the equation x + 3y = 9, we get:
When y = 6, x = -9
When y = -3, x = 18
So the intersection points of the two curves are (-9, 6) and (18, -3).
Now we can find the area between the two curves by splitting it into two regions: the region above the curve x + 3y = 9 and below the curve x + 9 = y², and the region below the curve x + 3y = 9 and above the curve x + 9 = y².
For the region above x + 3y = 9 and below x + 9 = y², we have:
a = 18
b = -9
f(x) = (y² - 9)/3
g(x) = (9 - x)/3
Alternatively, to compute the area between the two curves x + 3y = 9 and x + 9 = y² using a single integral, we need to express the area as a function of y instead of x.
We can rearrange the equations x + 3y = 9 and x + 9 = y² to get:
x = 9 - 3y
x = y² - 9
Setting these two expressions equal to each other, we get:
9 - 3y = y² - 9
Simplifying, we get:
y² + 3y - 18 = 0
Factorizing, we get:
(y + 6)(y - 3) = 0
So the solutions are:
y = -6 or y = 3
Substituting these values of y into the equation x + 3y = 9, we get:
When y = -6, x = 27
When y = 3, x = 0
So the intersection points of the two curves are (27, -6) and (0, 3).
The area between the curves can be expressed as the difference between the integrals of the curves' respective functions with respect to y, since the curves are better expressed in terms of y.
The function representing the curve x + 3y = 9 in terms of y is:
x = 9 - 3y
We can rearrange this equation to get:
y = (9 - x)/3
Substituting x = y² - 9, we get:
y = (9 - y² + 9)/3
Simplifying, we get:
y² + 3y - 18 = 0
This is the same equation we obtained before, so we know that the bounds of integration are -6 and 3.
The function representing the curve x + 9 = y² in terms of y is:
x = y² - 9
Substituting this expression into the formula for the area of a region between two curves, we get:
Area = ∫(y=α)^(y=β) [(9 - y²)/3 - (y² - 9)] dy
Where;
α = -6 and β = 3 are the bounds of integration, and
the integrand [(9 - y²)/3 - (y² - 9)] represents the difference between the y-values of the two curves at a given x-value.
Simplifying the integrand, we get:
Area = ∫(y=-6)^(y=3) (18 - 2y²)/3 dy
Integrating, we get:
Area = [(6y - (2/3)y³)/3] |(y=-6)^(y=3)
Plugging in the limits of integration, we get:
Area = [(18 - 216)/3] - [(-36 + 216)/3]
Simplifying, we get:
Area = 66
Learn more about area of curves here: https://brainly.com/question/30452445
#SPJ1
solve the system using elimination 2x+2y=62x-2y=6
Answers
Given the system of equations:
\(\begin{gathered} 2x+2y=6 \\ 2x-2y=6 \end{gathered}\)we can solve it using elimination by directly adding both equations to get the following:
\(\begin{gathered} 2x+2y=6 \\ 2x-2y=6 \\ ---------- \\ 4x=12 \\ \Rightarrow x=\frac{12}{4}=3 \\ x=3 \end{gathered}\)now that we have that x=3, we can find y using this value on any of the two equations:
\(\begin{gathered} 2x+2y=6 \\ x=3 \\ \Rightarrow2(3)+2y=6 \\ \Rightarrow6+2y=6 \\ \Rightarrow2y=6-6=0 \\ \Rightarrow2y=0 \\ y=0 \end{gathered}\)therefore, the solution of the system is (3,0)
A segment is on a number line with endpoints at -2.5 and 6. What is the length
of the segment?
Answers
Answer:
8.5
Step-by-step explanation:
-2.5 - 6 = -8.5, but if -8.5 is the length of the line, then it wouldn't be possible to differentiate between the 2 points and find the length of the segment. So how do we tackle this issue? Simple, just count how many paces the segment has gone through from -2.5 to 6. Then, you'll find that the answer ends up being 8.5. I hope this helps :)
a group of 60 students is randomly split into 3 classes of equal size. all partitions are equally likely. jack and jill are two students belonging to
Answers
The probability that Jack and Jill will end up in the same class is 19/59.
Principles of probability and counting:
The principles of probability and counting are fundamental concepts in probability theory and combinatorics. They are used to solve problems that involve uncertain events and counting arrangements of objects, respectively.
The principles of probability include:
Sample space: The set of all possible outcomes of a random experiment.
Event: A subset of the sample space.
Probability: A measure of the likelihood of an event, expressed as a number between 0 and 1.
Here we have
A group of 60 students is randomly split into 3 classes of equal size.
All partitions are equally likely. jack and jill are two students belonging to that group
Let's assume that Jack is assigned to a class, say the first class.
There are 20 students in that class, and the remaining 40 students are split evenly between the second and third classes.
Since all partitions are equally likely, each of the 59 remaining students has an equal chance of being assigned to any of the two remaining classes.
Now, we want to know the probability that Jill is assigned to the same class as Jack. There are 19 other students in the first class besides Jack, so there are 19 possible students in that class that Jill can be assigned to.
Out of the remaining 59 students, there are 40 in the other two classes, so Jill has 40 possible students she can be assigned to if she is not in Jack's class.
Hence,
The probability that Jill is assigned to the same class as Jack
= 19/59
Therefore,
The probability that Jack and Jill will end up in the same class is 19/59.
Learn more about Probability at
https://brainly.com/question/20893068
#SPJ4
Let f(x)=22−8−9.
(i)Write down the coordinates of the vertex.
(ii)Hence or otherwise, express the function in the form f(x)=2(−ℎ)2+.
b.Solve the equation f(x)=0.
Answers
There appears to be a typo in your function.
Note: f(x) = 22-8-9 is not a function. The notation f(x) means there should at least one x on the right side. Repost.
4. Consider the function f(x)=x^2-4
Part A: Write a function that shifts f(x) left 5 units.
Part B: Write a function that shifts f(x) right 8units.
Part C: Write a function that horizontally stretches f(x) by 1/4 units.
Part D: Write a function that horizontally compresses f(x) by 6 units.
HELP!!!! PLSSSS
Answers
Using translation concepts, it is found that the modified functions are:
A. \(g(x) = x^2 + 10x + 21\)
B. \(g(x) = x^2 - 16x + 60\)
C. \(g(x) = 16x^2 - 4\)
D. \(g(x) = \frac{x^2 - 4}{6}\)
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.In this problem, the function is given by:
\(f(x) = x^2 - 4\)
Item a:
For a shift left of 5 units, we have \(f(x + 5)\), hence:
\(g(x) = f(x + 5) = (x + 5)^2 - 4 = x^2 + 10x + 25 - 4 = x^2 + 10x + 21\)
Item b:
For a shift right of 8 units, we have \(f(x - 8)\), hence:
\(g(x) = f(x - 8) = (x - 8)^2 - 4 = x^2 - 16x + 64 - 4 = x^2 - 16x + 60\)
Item c:
For a horizontal stretch by a factor of 1/4, we find \(f(4x)\), hence:
\(g(x) = f(4x) = (4x)^2 - 4 = 16x^2 - 4\)
Item d:
For a vertical compression by a factor of 1/6, we find \(\frac{1}{6}f(x)\), hence:
\(g(x) = \frac{1}{6}f(x) = \frac{x^2 - 4}{6}\)
You can learn more about translation concepts at https://brainly.com/question/4521517
minimize f(x) = |x+3| + x^3 S.t. x sum [-2, 6]
Answers
Minimization of f(x) = |x+3| + x^3 at the endpoints (-2 and 6) the minimum value of the function is approximately 3.84, which occurs at x= \sqrt{1/3}
within the given interval.
To minimize the function subject to the constraint f(x) = |x+3| + x^3 that x lies in the interval [-2, 6], we need to find the value of x that minimizes f(x) within that interval.
First, let's analyze the function f(x). The absolute value term |x+3| can be rewritten as:
|x+3| =
x+3 if x+3 >= 0
-(x+3) if x+3 < 0
Since the interval [-2, 6] includes both positive and negative values of x+3, we need to consider both cases.
Case 1: x+3 >= 0
In this case, f(x) = (x+3) + x^3 = 2x + x^3 + 3
Case 2: x+3 < 0
In this case, f(x) = -(x+3) + x^3 = -2x + x^3 - 3
Now, we can find the minimum of f(x) within the given interval by evaluating the function at the endpoints (-2 and 6) and at any critical points within the interval.
Calculating the values of f(x) at x = -2, 6, and the critical points, we can determine the minimum value of f(x) and the corresponding value of x.
Since the equation involves both absolute value and a cubic term, it is not possible to find a closed-form solution or an exact minimum value without numerical methods or approximation techniques.
For more such questions on function
https://brainly.com/question/29631554
#SPJ8
given the least squares regression line y^= -2.88 + 1.77x, and a coefficient of determination of 0.81, the coefficient of correlation is:
a) -0.88
b)+0.88
c) +0.90
d)-0.90
Answers
The coefficient of correlation can be determined using the coefficient of determination, which is given as the square of the correlation coefficient. In this case, the coefficient of determination is 0.81, indicating that 81% of the variability in the dependent variable (y) can be explained by the independent variable (x).
To find the coefficient of correlation, we take the square root of the coefficient of determination. Taking the square root of 0.81 gives us 0.9. However, the coefficient of correlation can be positive or negative, depending on the direction of the relationship between the variables.
Looking at the given regression line y^= -2.88 + 1.77x, the positive slope of 1.77 indicates a positive relationship between x and y. Therefore, the coefficient of correlation would also be positive.
Hence, the answer is (c) +0.90, indicating a positive correlation between the variables.
Learn more about square root here: https://brainly.com/question/29286039
#SPJ11
B. Prove the following using indirect proof.
1. If x = 3, then 3x + 5 ≠10
2. If a triangle is an isosceles triangle ( 2 sides are equal), then the base angles
cannot measure 92 degrees.
3. Given: 3 - 5 ≠ 13
Prove: r≠6
4.Given: x = 5
Prove: 2x + 4 12
Answers
Answer:
jsjsusjsksksisidjjdsksjks
If the rate of inflation is 2.8% per year, the future price p(t) ( in dollars ) of a certain item can be modeled by the following exponential function, where t is the number of years from today p(t) = 1200(1.028)tfind the current price of the item and the price 9 years from today. Round your answers to the nearest dollar as necessary. Current price: _$ Price 9 years from today: _$

Answers
If it's 9 years, then you have to replace t = 9 in the expression that models the price. With that we have the price 9 years from today:
\(p(t)=1200\cdot1.028^9=1200\cdot1.282=1538.577\)Rounded to the nearest dollar, the price 9 years from today is $1539
And the current price is the first number of the expression: $1200
Help me plsssssssssss

Answers
Answer:
#1: slope = 1/10
#2: slope = 5/2
#3: slope = 1/2
#4: slope = - 10/9
Sry if this is wrong but i hope i helped :)
531
x 47
Long multiplication :) please help
Answers
we are interested in testing whether the variance of a population is significantly more than 484. what is the null hypothesis for this test? h0 : 2 ≥ 484 h0 : 2 > 484 h0 : 2 ≤ 22 h0 : 2 ≤ 484
Answers
The null hypothesis for this test is: H0 : σ² ≤ 484.
In hypothesis testing, the null hypothesis (H0) is a statement that we assume to be true unless we have sufficient evidence to reject it. It is typically a statement of no effect, no difference, or no relationship between variables.
In this case, we are interested in testing whether the variance of a population is significantly more than 484. So the null hypothesis would be that the population variance is less than or equal to 484, which can be represented as:
H0: σ2 ≤ 484
This means we assume that the population variance is not significantly more than 484, unless we have sufficient evidence to reject this assumption based on the sample data.
Thus, the null hypothesis is H0 : σ² ≤ 484.
Learn more about "null hypothesis":
https://brainly.com/question/25263462
#SPJ11
9+3.5g=11−0.5g i need this anwser plz help
Answers
Answer:
g = 1/2
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASEquality PropertiesStep-by-step explanation:
Step 1: Define equation
9 + 3.5g = 11 - 0.5g
Step 2: Solve for g
Add 0.5g on both sides: 9 + 4g = 11Subtract 9 on both sides: 4g = 2Divide 4 on both sides: g = 1/2Step 3: Check
Plug in g into the original equation to verify it's a solution.
Substitute in g: 9 + 3.5(1/2) = 11 - 0.5(1/2)Multiply: 9 + 1.75 = 11 - 0.25Add/Subtract: 10.75 = 10.75Here we see that 10.75 does indeed equal 10.75.
∴ g = 1/2 is a solution of the equation.
Answer: g= 0.5
Step-by-step explanation:
Add
3.5g and 0.5g. to get
9+4g=11
then subtract 9 from the 11 and you should get 4g=2.
then divide 4 from 2 and you should get the answer of 2/4.
simplify it and you should get the answer g=0.5
What are the x-intercepts
1. (x - 12) (x + 6) = 0
Answers
( x - 12 ) ( x + 6 ) = 0
x - 12 = 0 and x + 6 = 0
x = 12 and x = -6
Answer:
\(x=12,\:x=-6\) are your x intercepts
Step-by-step explanation:
\(\left(x-12\right)\left(x+6\right)=0\\\mathrm{Using\:the\:Zero\:Factor\:Principle:\quad \:If}\:ab=0\:\mathrm{then}\:a=0\:\mathrm{or}\:b=0\:\left(\mathrm{or\:both}\:a=0\:\mathrm{and}\:b=0\right)\\\mathrm{Solve\:}\:x-12=0:\quad x=12\\x-12=0\\\mathrm{Add\:}12\mathrm{\:to\:both\:sides}\\x-12+12=0+12\\Simplify\\x=12\\\mathrm{Solve\:}\:x+6=0:\quad x=-6\\x+6=0\\\mathrm{Subtract\:}6\mathrm{\:from\:both\:sides}\\x+6-6=0-6\\Simplify\\x=-6\\The\:solutions\:to\:the\:quadratic\:equation\:are:\\x=12,\:x=-6\)
i need this asap so can someone answer

Answers
0.2
0.2y+0.4
I think this should be correct
On a chemistry quiz, there are 5 multiple choice questions with 4 choices each. What is the probability that you get a 100% if you strictly guess.
Answers
Answer:
0.097%
Step-by-step explanation:
Since this is a series of events probability question, in order to calculate the probability you need to first find the probability of getting each individual answer right and then multiplying those probabilities together. This will give you the probability of getting 100% on the entire test. Since the questions are multiple-choice with 4 choices and only 1 correct choice then the probability of getting one right is 1/4 or 25%. Now that we have that probability we simply need to multiply it 5 times for each individual question.
1/4 * 1/4 * 1/4 * 1/4 * 1/4 = 1/1024 or 0.0009765 or 0.097%
Patrick is excited to attend his son’s soccer game tomorrow
evening, but he also needs to ensure his daughter arrives at her
coding class on time. Patrick is debating whether taking the train
or his
Answers
Personal car would be the best option to manage both tasks efficiently. While the train is a reliable mode of transportation, it may have fixed schedules that might not align perfectly with Patrick's needs.
On the other hand, using his personal car provides more flexibility and allows him to tailor the departure time according to his daughter's coding class schedule.
If Patrick decides to take the train, he would need to check the train schedule to see if there are convenient departure and arrival times for both the soccer game and the coding class. This option would require planning and coordination to ensure he arrives at the game on time and can pick up his daughter afterward.
Using his personal car gives Patrick the freedom to leave at a time that accommodates both the soccer game and the coding class. He can drop off his daughter at her coding class, attend the soccer game, and then pick her up afterward without being restricted by train schedules.
Considering the circumstances, Patrick might find it more convenient to use his personal car to manage both tasks effectively and ensure he can attend his son's soccer game while also ensuring his daughter arrives at her coding class on time.
To learn more about transportation
https://brainly.com/question/32750280
#SPJ11
You are dealt one card from a standard 52-card deck. Find the probability of being dealt a five.
Answers
1/13
Explanations:Probability is the likelihood or chance that an event will occur. Mathematically;
\(\text{Probability}=\frac{Expected\text{ outcome}}{Total\text{ outcome}}\)Since there are 52 cards in a deck of cards, hence the total outcome will be 52.
Next is to get the expected outcome. Since we need the probability of being dealt a five and there 4 fives in a deck of cards. The expected outcome will be 4
The required probability is expressed as:
\(\begin{gathered} \text{ Pr(dealt with a five)=}\frac{4}{52} \\ \text{ Pr(dealt with a five)=}\frac{1}{13} \end{gathered}\)Hence the probability of being dealt a five is 1/13
The ratio of girls to boys in chess club is 3:4. There are 35 total members. How many boys were there?
Answers
4/7=x/35
Cross multiply
7x=140 divide 7 on both sides
Your answer is x= 20
Pls give brainliest, thank u
help you guys plssss and add an explanation

Answers
Answer:
100 degrees
Step-by-step explanation:
angles in a quadrilateral (4-sided shape) sum to 360 degrees
so add all the angles up together (80+75+105=260)
and then subtract it from 360 (so it's 100)
Answer:
100 degrees
Step-by-step explanation:
sum of all interior angles of a quadrilateral =360 degrees
80 + 75+ 105=260
360-260=100 degrees
The paragraph below comes from the rental agreement Susan signed when she opened her account at Super Video.
“All rentals are due back by midnight of the due date as printed on the transaction receipt. Any rental not received by midnight on the day it is due is subject to a late charge of $1.50 for each day it is late. Any rental not returned by the fifth day after the due date will be transferred to a sale. The Customer will then be required to pay the purchase price of the item in addition to five (5) days of late fees. The Customer will not be required to return the product once the total balance is paid.”
Both of Susan’s movies are three days late. According to her receipt, the purchase price of one of her movies is $12.00 while the purchase price for the other movie is $15.00. If she turns both of them in today, how much will Susan owe Super Video?
A) $4.50
B) $9.00
C) $27.00
D)$38.00
Answers
Answer:
$9
Step-by-step explanation:
(2 movies returned late)
3 days late
$1.50 per day late fee
equaling $4.50 per movie
TOTALING $9
TOTALING $9.00
Answer:
B) $9.00Step-by-step explanation:
Since its less than 5 days, Susan will have to pay only late charge fee for two movies for 3 days.
The amount to be paid:
3*2*$1.5 = $9Correct choice is B