PLEASE HELP ASAP
Write a polynomial of the smallest degree with roots 1, -3, and 4.
Answers
Answer:
x^3 - 2x^2 - 11x +12
Step-by-step explanation:
If 1 is a root, then x-1 is a factor
If -3 is a root, then x+3 is a factor
If 4 is a root, then also x-4 is a factor
A product of the three factors gives us the polynomial
(x-1)(x+3)(x-4) = (x^2 +2x - 3)(x-4)
= x^3 - 2x^2 - 11x +12
Related Questions
Find n so that T_n (trapezoid rule with n subintervals) is guaranteed to approximate integral_0^5 cos (3 x) dx/to with 0.02 a) n ≥ 34 b) n ≥ 69 c) n ≥ 63 d) n ≥ 59 e) n ≥ 17
Answers
The smallest value of n greater than 8 among the options is 17. Therefore, the correct answer is e) n ≥ 17.
To find the appropriate value of n for the trapezoid rule to approximate the integral with an error less than 0.02, we can use the error-bound formula for the trapezoid rule:
Error ≤ (b - a)³ * M / (12 * n²)
where a and b are the limits of integration, M is the maximum value of the second derivative of the function in the interval [a, b], and n is the number of subintervals.
For the function f(x) = cos(3x), the second derivative is f''(x) = -9cos(3x). The maximum value of |f''(x)| in the interval [0, 5] is 9.
Plugging in the values, we get:
0.02 ≥ (5 - 0)³ * 9 / (12 * n²)
Now we solve for n:
0.02 ≥ 125 * 9 / (12 * n²)
n² ≥ 125 * 9 / (12 * 0.02)
n² ≥ 56.25
n ≥ √56.25 ≈ 7.5
Since n must be an integer, we round up to the nearest integer: n ≥ 8.
However, this value of n is not among the given options. The smallest value of n greater than 8 among the options is 17. Therefore, the correct answer is: e) n ≥ 17
The error bound for the trapezoid rule is given by:
|error| ≤ K(b-a)³ / (12n²)
where K is the maximum value of the second derivative of the function being integrated. In this case, K = 9, since the second derivative of cos(3x) is -9cos(3x).
We want to find n such that the error is less than or equal to 0.02. So we have:
0.02 ≤ 9(5-0)³ / (12n²)
0.02 ≤ 1125 / n²
n² ≤ 56250
n ≤ 237.16
Since n has to be an integer, the smallest value of n that satisfies this inequality is n = 238. Therefore, the answer is:
n ≥ 238 which is not one of the given choices. However, the closest choice is: b) n ≥ 69 which is incorrect. So the answer is none of the above.
Learn more about Trapezoid Rule here: brainly.com/question/30514442
#SPJ11
PLEASE HELP 25 POINTS PLUS BRAINLIEST

Answers
The missing length of the triangle using Pythagoras theorem is; x = 3
How to use Pythagoras Theorem?Pythagoras Theorem is defined as the way in which you can find the missing length of a right angled triangle. The right angle triangle has three sides, the hypotenuse (which is always the longest), Opposite (which doesn't touch the hypotenuse) and the adjacent (which is between the opposite and the hypotenuse).
The formula to find the sides is;
hypotenuse² = opposite + adjacent²
We are given;
Hypotenuse = 5
Opposite = x
adjacent = 4
Thus;
5² = x² + 4²
x² = 5² - 4²
x² = 25 - 16
x = √9
x = 3
We conclude that it is the missing length of the triangle
Read more about Pythagoras Theorem at; https://brainly.com/question/231802
#SPJ1
The sum of -14 and a number is positive. Identify a possible value for that number
Explain your selection
Answers
Answer:
15
Step-by-step explanation:
Since, we need a number that if added to -14, it'll give a positive result. The first number is gonna be 15, . Because, it's the first number that can give a positive number if summed up with -14.
what is the value of 30-2(7+2)-1
Answers
Answer:
11
Step-by-step explanation:
30-2(7+2)-1
30-2(9)-1
30-18-1
12-1
11
Answer: Thy answer to ye question is 11
Step-by-step explanation:
Reuben Araújo received a $800 discount loan to purchase a washer and dryer. The loan was offered at 10% for 120 days. What are the proceeds?
$
Answers
The proceeds on the loan is $9600
Data;
Principal = $800Rate = 10% = 0.1Time = 120 daysSimple InterestSimple InterestTo solve this problem, we need to calculate the simple interest of the loan which is done by the formula below
\(S.I = PRT\)
P = principalR = rateT = timeLet's substitute the values into the equation and solve
\(S.I = 800*0.1*120\\ S.I = 9600\)
The proceeds on the loan is $9600
Learn more on simple interest here;
https://brainly.com/question/26066433
A car travels 80 millimetres in 2 1/2 hours . What is it speed in kilometres per hour
Answers
Answer:
32 Kilometers
Step-by-step explanation:
A Car travels 80 Kilometers in 2 and Half hours.
1 Hour =60 minutes, 2 & Half hours= 2.5*60= 150 minutes
Kilometers travelled by Car in a hour= 80/150*60= 32 Kilometers
How many bricks each 25 cm by 15 cm by 8 cm, are required for a wall 32 m long, 3 m high and 40 cm thick?
Answers
Answer:
8
Step-by-step explanation:
81. Volume of a cone: 1. V = (1/3)πr2h 2. Slant height of a cone: 1. s = √(r2 + h2) 3. Lateral surface area of a cone: 1. L = πrs = πr√(r2 + h2) 4. Base surface area of a cone (a circle): 1. B = πr2 5. Total surface area of a cone: 1. A = L + B = πrs + πr2 = πr(s + r) = πr(r + √(r2 + h2))
hope this helps
What does the expected value of a binomial distribution with n trials tell you? PICK ONE OF THE FOLLOWING.
1.the average number of successes
2. the average number of failures
3. the standard deviation of failures
Answers
By examining the expected value of a binomial distribution with n trials, (1) we may determine the typical number of successes.
What is binomial distribution?The binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a series of n independent experiments, each asking a yes-or-no question and each with its own Boolean-valued outcome: success (with probability p) or failure (with probability q=1-p).
This distribution is used in probability theory and statistics.
A Bernoulli trial, or experiment, is another name for a single success-or-failure experiment, and a Bernoulli process is another name for a series of results.
For a single trial, or n = 1, the binomial distribution is a Bernoulli distribution.
The popular binomial test of statistical significance is based on the binomial distribution.
We may find out the average number of successes by looking at the expected value of a binomial distribution with n trials.
Therefore, by examining the expected value of a binomial distribution with n trials, (1) we may determine the typical number of successes.
Know more about binomial distribution here:
https://brainly.com/question/9325204
#SPJ4
N architect is standing 370 feet from the base of a building and would like to know the height of the building. If he measures the angle of elevation to be 50°, what is the approximate height of the building?
Answers
Answer:
h = 440.94 feet
Step-by-step explanation:
It is given that,
An architect is standing 370 feet from the base of a building, x = 370 feet
The angle of elevation is 50°.
We need to find the approximate height of the building. let it is h. It can be calculated using trigonometry as follows :
\(\tan\theta=\dfrac{P}{B}\\\\\tan\theta=\dfrac{h}{x}\\\\h=x\tan\theta\\\\h=370\times \tan50\\\\h=440.94\ \text{feet}\)
So, the approximate height of the building is 440.94 feet
micah is 111 of 282828 students in a class. micah's teacher is going to randomly select 333 students from their class to visit a classroom of younger students. what is the probability micah is included in the group of students chosen?
Answers
0.71% is the probability micah is included in the group of students chosen.
Describe probability using an example?
By dividing the number of favorable outcomes by the total number of possible outcomes, probability—the likelihood that an event will occur—is determined.The simplest example is a coin flip. When you flip a coin there are only two possible outcomes, the result is either heads or tails.the probability micah is included in the group of students chosen =
3/28 = 10.71%
The probability of her getting picked is unlikely.
Learn more about Probability
brainly.com/question/11234923
#SPJ9
The complete question is -
Micah is 1 of 28 students in a class. Micah's teacher is going to randomly select 3 students from their class to visit a classroom of younger students. What is the probability Micah is included in the group of students chosen?
Can you help me with this please? because I am confused

Answers
Answer:
Make a line a bit close to -1
Step-by-step explanation:
-2 3/4 can be re-written as -2.75 therefore you have to mark close to the number -1
The computer was regularly priced at $1,800. If you order the computer over the Internet, you can save money as the price is only $1,100. What percent discount are you getting?
Answers
11 / 18 = 61%
39% discount given
*EXTRA PTS* how do you solve 2x^6 x 5x^3 ?
Answers
Answer:
10x^9
Step-by-step explanation:
Add the exponents together and multiply normally
2x^6+5x^3
=10x^9
Answer:
2x^6x+5x^3
Step-by-step explanation:
First you want to
Add the exponents like you would with regular numbers
Which comes out to
2
Steven and Bob both have a Pokemon card collection. The number of Pokemon cards in Steven's collection can be represented by x. The number of cards in Bob's collection is 4 times the amount in Steven's collection. The total number of Pokemon cards in both collections is 240. What is the number of cards in Steven's collection?
Answers
Answer: 48
Step-by-step explanation:
The number of Pokemon cards in Steven's collection = x
The number of cards in Bob's collection is 4 times the amount in Steven's collection= 4x
The total number of Pokemon cards in both collections = 240
x + 4x = 240
5x = 240
x = 240/5
x = 48
The number of cards in Steven's collection is 48
Billy is running away from a Wells Fargo bank at a speed of 13 kilometers per hour (units are km/h ). If the distance between the bank and the border to Mexico is 1.9 km, will he be able to get there before the cops arrive in 9 minutes? How long will it take for him to reach the border? (Hint: speed = distance / time, 1 hour =60 minutes )
Answers
No, Billy will not be able to reach the border before the cops arrive in 9 minutes.
To determine whether Billy can reach the border before the cops arrive, we need to calculate the time it would take him to cover the distance of 1.9 km.
Using the formula speed = distance / time, we can rearrange the formula to solve for time. Rearranging, we have time = distance / speed.
Given that Billy's speed is 13 km/h, we can calculate the time it would take him to cover 1.9 km.
time = 1.9 km / 13 km/h = 0.146 hours
To convert hours to minutes, we multiply by 60:
0.146 hours * 60 minutes/hour = 8.76 minutes
Therefore, it would take Billy approximately 8.76 minutes to reach the border. Since the cops are expected to arrive in 9 minutes, he would not be able to make it before they arrive.
Learn more about distance here : brainly.com/question/15256256
#SPJ11
Find h(x, y) = g(f(x, y)) and the set on which h is continuous.
g(t) = t2 + f(x, y) = 2x + 3y − 6
Answers
H(x,y) is a continuous function for all real values of x and y.
The function h(x, y) is defined as h(x, y) = g(f(x, y)) = g(2x + 3y − 6). We can calculate the value of h(x, y) by substituting f(x, y) into g(t):
h(x, y) = \((2x + 3y − 6)^2 + (2x + 3y − 6) = 4x^2 + 12xy − 24x + 9y^2 − 36y + 36 + 2x + 3y − 6 = 4x^2 + 14xy − 22x + 9y^2 − 33y + 42.\)
For h(x, y) to be continuous, the set of points at which the function is continuous must exist. This set includes all points (x, y) such that \(4x^2 + 14xy − 22x + 9y^2 − 33y + 42\) is defined, i.e. all real values of x and y. Thus, h(x, y) is continuous for all real values of x and y.
H(x,y) is a continuous function for all real values of x and y.
Learn more about continuous function here:
https://brainly.com/question/21447009
#SPJ4
a set of values for the decision variables that satisfy all the constraints and yields the best objective function value is
Answers
A set of values for the decision variables that satisfy all the constraints and yields the best objective function value is a feasible solution that optimizes the objective function.
In optimization problems, decision variables are the quantities that we can control or adjust to achieve a desired outcome. Constraints are the limitations or conditions that these decision variables must satisfy. The objective function represents the goal or objective we want to optimize.
A feasible solution refers to a set of values for the decision variables that satisfy all the given constraints. This means that the solution meets all the specified requirements and does not violate any constraints. However, there can be multiple feasible solutions that meet the constraints.
Among these feasible solutions, the one that yields the best objective function value is the optimal solution. The objective function value is a measure of how well the solution aligns with the desired objective. The goal is typically to maximize or minimize this objective function value, depending on the problem.
To know more about objective function,
https://brainly.com/question/31841664
#SPJ11
Suppose that the functions u and w are defined as follows.
u(x)=-x-1
w(x) = 2x+1
Find the following.

Answers
Step-by-step explanation:
I answered this already.
What is the length of the arc by a central angle of 85 degrees and a radius of 8cm to the nearest tenth of a cm?

Answers
9514 1404 393
Answer:
11.9 cm
Step-by-step explanation:
Arc length is given by ...
s = rθ . . . . . . θ is the central angle in radians
Your central angle is 85°, so is (85/180)π radians = 17/36π radians.
Then the arc length is ...
s = (8 cm)(17/36π) ≈ 11.9 cm
The length of the 85° arc is about 11.9 cm.
Q9.
£4000 is invested at 2% compound interest.
(a) What is the value of the investment after 3 years?
Answers
Answer:
£4244.83
Step-by-step explanation:
Use the compound amount formula:
A = P(1 + r)^t. Here, P = £4000, r = 0.02 and t = 3 yrs
So: A = £4000(1 + 0.02)^3, which comes to:
A = £4000(1.061) = £4244.83
Consider the following system of equations.
1. 75x + 1. 25y = 2. 75
7x + 5y = 9
What is the solution to the system?
Since 11 ≠ 9, there is no solution.
Since 0 = 0, there are infinitely many solutions.
There is one solution, x = 0 and y = 0.
There are two solutions (11, 0) and (0, 9)
Answers
Multiply the upper system by -4:
\( - 7x - 5y = - 11\)
\(7x + 5y = 7\)
\(0 = - 3\)
\(this \: system \: admits \: no \: solutions\)
Prove for every integer n > 7 that there exist positive integers a and b such that n = 2a + 3b.
Answers
For every integer n > 7, we have shown that there exist positive integers a' and b' such that n = 2a' + 3b'.
What is an integer?An integer is a mathematical concept used to represent whole numbers, both positive and negative, without any fractional or decimal parts. Integers include zero (0) and the positive and negative counting numbers (1, 2, 3, ... and -1, -2, -3, ...). Integers can be expressed as numbers on the number line that extend infinitely in both the positive and negative directions.
To prove that for every integer n > 7, there exist positive integers a and b such that n = 2a + 3b, we can use the concept of the Chicken McNugget theorem, also known as the Frobenius coin problem.
The Chicken McNugget theorem states that for any two relatively prime positive integers a and b, the largest integer that cannot be expressed as a non-negative integer combination of a and b is ab - a - b.
In our case, a = 2 and b = 3 are relatively prime since their greatest common divisor (GCD) is 1.
Let's consider the number 6. We can express 6 as 2 * 1 + 3 * 2, so it is possible to represent 6 using positive integers a and b.
Now, let's consider any number n > 7. We know that n - 6 is a positive integer greater than or equal to 2. Therefore, n - 6 can be expressed as a non-negative integer combination of 2 and 3, using the Chicken McNugget theorem.
So, n - 6 = 2a + 3b, where a and b are positive integers. Adding 2 * 1 + 3 * 2 to both sides of the equation, we get:
n = 2a + 3b + 6
We can see that by choosing a = a + 1 and b = b + 2, we can rewrite the equation as:
n = 2(a + 1) + 3(b + 2) = 2a' + 3b',
where a' and b' are positive integers.
Therefore, for every integer n > 7, we have shown that there exist positive integers a' and b' such that n = 2a' + 3b'.
To know more about integers follow the given link:
https://brainly.com/question/929808
#SPJ4
2. Mario moved from a city to a small town. The population of the
city is 6 x 105, which is about 15 times larger than the town. Which
expression could represent the approximate population of the small
town?
Answers
Answer:
the answer is 4 x 10^4 or 40,000
Step-by-step
the answer is 40,000 but you need to put it in scientific notation which equals 4 x 10 to the 4th power
4 x 10^4
Which of the following situations best matches the data in the table?
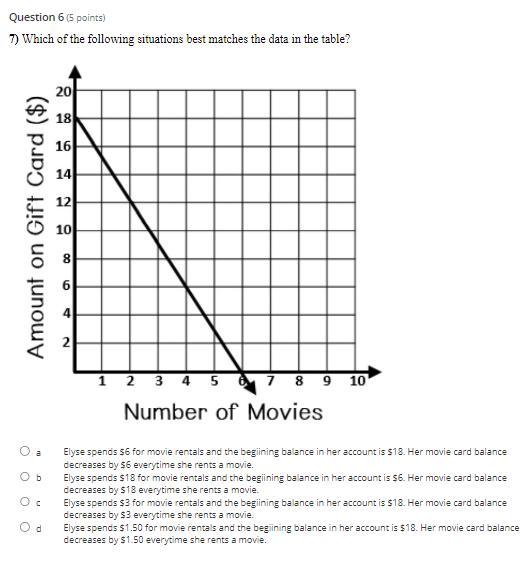
Answers
Based on the graph, the situation that best matches what the data on the table shows is C. Elyse soends $3 for movie rentals and the beginning balance in her account is $18. Her movie card balance decreases by $3 everytime she rents a movie.
What does the data on the graph show?The data on the graph shows the amount of money that was spent by Elyse for every movie she rented. She did so with the use of a gift card. Based on the fact that the graph begins at $18, this means that the amount on the gift card was $18.
The amount that Elyse spent per movie was:
= Change in amount on gift card / Change in movies rented
= (18 - 12) / (2 - 0)
= 6 / 2
= $3
Elyse therefore spent $3 whenever she rented a movie.
Find out more on matching data at https://brainly.com/question/23957040
#SPJ1
Solve by substitution. Please show work
Y=-3x-14
-2x-y=9
Answers
Answer:
The value of x is -5 and y is 1
Step-by-step explanation:
Here,
y = -3x - 14
-2x - y = 9
Substitution Method
y = -3x - 14 ...(1)
-2x - y = 9 ...(2)
Now, substitute the value of y = -3x - 14 in equation (2) we get,
-2x - y = 9
-2x - (-3x - 14) = 9
-2x + 3x + 14 = 9
x = 9 - 14
x = -5
Now, put the value of x in equation (1) we get,
y = -3x - 14
y = -3(-5) - 14
y = 15 - 14
y = 1
Thus, The value of x is -5 and y is 1
FOR VERIFICATION ONLY:y = -3x - 14
1 = -3(-5) - 14
1 = 15 - 14
1 = 1
-2x - y = 9
-2(-5) - 1 = 9
10 - 1 = 9
9 = 9
Hence, L.H.S = R.H.S
-TheUnknownScientist
The amount of money Deon earns working at a store is given in the table.
Deon's Earnings
Hours Worked
3
5
7
9
11
Money Earned $37.50 $62.50 $87.50 $112.50 $137.50
How much money does he earn for working 20 hours at the store?
O $12.50
0 $125.00
O $250.00
O $150.00

Answers
C.
Explanation:
I had the quiz as well :)
If the amount of money Deon earns working at a store is given in the table. He will earn $20 in the 20 hours.
What is a proportional relationship?It is defined as the relationship between two variables when the first variable increases, the second variable also increases according to the constant factor.
The given data is represented by a table that gives a relation between the money earned and the hour he works.
It is obtained that there is a proportional relationship obtained from the money earned and the hour he works as,
The rate when he worked for 3 hours.
r=Money earned / hour
r=$ 37.50 / 3
r=12.5
The rate when he worked for 6 hours.
r=Money earned / hour
r=$ 62.50 / 6
r=12.5
The rate when he worked for 7 hours.
r=Money earned / hour
r=$ 87.50 / 7
r=12.5
The amount he earned for 20 hour is the product of the amount he earned for the one hour and the number of hours,
=$ 12.5 × 20
= $250.00
Thus, the amount of money Deon earns working at a store is given in the table. He will earn $20 in the 20 hours.
Learn more about the proportional here:
brainly.com/question/14263719
#SPJ5
a regular hexagon has side length $6$. if the perimeter and area of the hexagon are $p$ and $a$, respectively, what is the value of $\frac{p^4}{a^2}$?
Answers
If the perimeter and area of the hexagon are $p$ and $a$, respectively, the value of $\frac{p^4}{a^2}$ is 192.
Regular hexagon has side length of 6
Perimeter of regular hexagon is given by 6*(side)
∴Perimeter = 6*(6) = 36
A closed path that covers, encircles, or outlines a one-dimensional length or a two-dimensional shape is called a perimeter.
Area of Regular hexagon is composed of 6 equilateral triangles and is given by,
= 6* (1/2)*6² * √3/2
= 3√3/2 * 36
= 54√3
The size of a patch on a surface is determined by its area. Surface area refers to the area of an open surface or the boundary of a three-dimensional object, whereas the area of a plane region or plane area refers to the area of a form or planar lamina.
So fraction \(\frac{p^4}{a^2}\) = \(\frac{36^4}{(54\sqrt{3})^2 } = \frac{36*36*36*36}{54*54*3}\) =192.
Learn more about Hexagon :
https://brainly.com/question/27178769
#SPJ4
a person bought two old scooters for rs. 9000. by selling one at a profit of 25% and the other at a loss of 20%, to neither gain nor loses. the cost of each scooter is
Answers
A person bought two old scooters for Rs. 9000. By selling one at a profit of 25% and the other at a loss of 20%, to neither gain nor lose. The cost of each scooter is Rs. 4000 and Rs. 5,000.
Let the cost price of the first scooter be Rs. x and the cost price of the second scooter = Rs. (9000 - x)
Given, the first scooter was sold at a profit of 25%.
Selling price of first scooter = x + 0.25x = 1.25x
Given, the second scooter was sold at a loss of 20%.
Selling price of second scooter = 0.8(9000 - x)
Now, according to the question, there is no profit and no loss.
Therefore, Total Selling Price = Cost Price=> (1.25x) + 0.8(9000 - x) = 9000=> 1.25x + 7200 - 0.8x = 9000=> 0.45x = 1800=> x = Rs. 4000
So, the cost price of the first scooter is Rs. 4000.
The cost price of the second scooter is Rs. (9000 - 4000) = Rs. 5000
Therefore, the cost of each scooter is Rs. 4000 and Rs. 5,000.
Know more about Profit and Loss here :
https://brainly.com/question/1358513
#SPJ11
Solve for x: 3/4x + 1/4 =2x
Answers
Answer:
x=1
Step-by-step explanation:
3/4x + 1/4 =2x
3/4x=2x-1/4
3/4x-2x= -1/4
3/4x-8/4x= -1/4
-5/4x= -1/4
x= -1/4+ 5/4
x=4/4
x=1
Answer:
x = 1/5
Step-by-step explanation:
Simplfy:
3x/4 + 1/4 = 2x
Join the denominators:
3x + 1/4 = 2x
Multiply both sides by 4:
3x + 1 = 8x
Subtract 3x from both sides:
1 = 8x - 3x
Simplify:
1 = 5x
Divide both sides by 5:
x = 1/5
How do you think mental health is similar to physical health?
Who ever answers first gets 20$ no cap
Answers
Answer:
Poor physical health can lead to an increased risk of developing mental health can negatively impact on Physical health leading to an increased risk of some conditions
Step-by-step explanation:
The association between mental and physical health are poor mental is a risk factor for chronic physical conditions . if this is not correct don't report me or blame me just trying to help ......