Answers
Answer:
Step-by-step explanation:
1. there is 4 zeros in 10 4, the product is 10,000
2. 100,000
3. 100
Answer:
its 100000
Step-by-step explanation:
10×10=100×10=1000×10=10000×10=100000
Related Questions
What is the length of Vz?
2 units
6 units
8 units
10 units
Answers
I will give brainiest to whoever answers correctly !!
Please do not steal my points I'm tired of it put a legit answer or leave!! I will give brainiest to whoever answers correctly!!

Answers
Answer:
15450
Step-by-step explanation:
Makayla’s local movie theater has a moviegoer club. The charts in the annual registration fee of $25. However movie tickets are discounted remembers at six dollars per ticket instead of the regular nine dollars per ticket. Let him represent the number of movie tickets Makayla’s purchase a need to write a function tomorrow the amount of money Makayla spent going to the movies doing the club
Answers
Answer:
m = 25 + 6n
Step-by-step explanation:
To write a function for the amount of money Makayla spent going to the movies during the club, you need to consider two things: the annual registration fee and the discounted ticket price. The annual registration fee is a fixed amount that does not depend on the number of movie tickets Makayla purchases. The discounted ticket price is a variable amount that depends on the number of movie tickets Makayla purchases. You can use a letter, such as n, to represent the number of movie tickets Makayla purchases. Then, you can write an expression for the amount of money Makayla spent on movie tickets, which is 6 times n, or 6n. To find the total amount of money Makayla spent going to the movies during the club, you need to add the annual registration fee and the amount of money spent on movie tickets. This gives you the expression 25 + 6n. You can use another letter, such as m, to represent the total amount of money Makayla spent going to the movies during the club. Then, you can write an equation that relates m and n, which is m = 25 + 6n. This equation is a function that models the amount of money Makayla spent going to the movies during the club as a function of the number of movie tickets she purchased.
Question 4 (1 point)
Cookie Monster bought four packs of chocolate cookies and three packs of butter cookies for $17. Two packs of
butter cookies cost $6. All chocolate cookies cost the same and all butter cookies cost the same. What is the ratio of
the cost of a pack of chocolate cookies to the cost of a pack of butter cookies?
Answers
2:3
6 ÷ 2 = $3 (cost of 1 pack of butter cookies)
3 x 3 = 9 (cost of 3 packs of butter cookies)
17 - 9 = 8 (cost of 4 packs of chocolate cookies)
8 ÷ 4 = 2 (cost of one pack of chocolate cookies)
The initial size of a culture of bacteria 1100. After 1 hour, the bacteria count is 9500.
Find the function n(t)=no
that models the population after
hours.
Find the population after 1.5 hours.
Then Find the number of hours when the number of bacteria will reach 20,000.
Sketch the graph of the population function.
Answers
To find the function n(t) that models the population of bacteria after t hours, we can use the exponential growth formula:
n(t) = n0 * e^(kt)
Where:
n(t) is the population after t hours,
n0 is the initial population size,
e is the base of the natural logarithm (approximately 2.71828),
k is the growth rate constant.
We can determine the value of k using the given information. After 1 hour, the bacteria count is 9500, which is the population at time t = 1. Plugging these values into the equation:
\(9500 = 1100 * e^(k*1)\)
To find k, we can divide both sides by 1100:
9500/1100 = e^k
Now, we can solve for k by taking the natural logarithm (ln) of both sides:
ln(9500/1100) = ln(e^k)
ln(9500/1100) = k
Now we have the value of k. We can plug it back into the exponential growth formula to obtain the function n(t):
\(n(t) = 1100 * e^(ln(9500/1100) * t)\)
To find the population after 1.5 hours, we can substitute t = 1.5 into the equation:
\(n(1.5) = 1100 * e^(ln(9500/1100) * 1.5)\)
To find the number of hours when the number of bacteria will reach 20,000, we can set n(t) equal to 20,000 and solve for t:
\(20,000 = 1100 * e^(ln(9500/1100) * t)\)
Finally, to sketch the graph of the population function, plot the values of t on the x-axis and the corresponding values of n(t) on the y-axis using the equation n(t) = 1100 * e^(ln(9500/1100) * t). The resulting graph will show the exponential growth of the bacteria population over time.
For more such questions on exponential
https://brainly.com/question/30166689
#SPJ8
Keiko is going for a walk.she takes 3 hours to walk 7.5 miles.what is her speed
Answers
Answer:
2.5 mph
Step-by-step explanation:
Patricia is making homemade snacks. Each snack requires 2.25 cups of almonds. Patricia buys 6 cans of almonds that each contain eight 1/3 cup servings. What is the maximum number of snack bags that Patricia can make with the almonds?
Answers
Answer: 7
Step-by-step explanation:
Patricia has 6 cans of almonds that each contain eight 1/3 cup servings, meaning that Patricia has a total of
6 cans x 8 servings x 1/3 cup = 16 cups of almonds
If she needs 2.25 cups of almonds, that would be equal to
16/2.25 = around 7.1
since you can't have a fraction of a snack bag, Patricia just has 7 snack bags.
I’m about to cry from frustration. Help please before I die

Answers
Answer:
\(\frac{1}{3}x+16=37\)
63 Jelly Beans
Step-by-step explanation:
The unknown is the number of jelly beans originally in the bag or x
First he had x jelly beans
The he ate one-third of them
\(\frac{1}{3}x\)
He then ate 16 more jelly beans
\(\frac{1}{3}x+16\)
This was equal to 37 jelly beans
\(\frac{1}{3}x+16=37\)
This is the equation
Now solve for x
Subtract 16 from both sides
\(\frac{1}{3}x=21\)
Multiply both sides by 3
\(x=63\)
63 Jelly Beans
determine the value of b²- 4ac
12x² + 5x -2=0
Answers
In this case, we have:
a = 12
b = 5
c = -2
Now we can substitute these values into the formula for b²-4ac:
b²-4ac = (5)² - 4(12)(-2)
Simplifying, we get:
b²-4ac = 25 + 96
b²-4ac = 121
Therefore, the value of b²-4ac for the quadratic equation 12x² + 5x - 2 = 0 is 121.
Does the expression x^3-1 divided by x^2 -1 simplify to x?
Answers
No, the expression (x^3 - 1) / (x^2 - 1) does not simplify to x.
To simplify the expression, let's first factorize both the numerator and denominator.
The numerator can be factorized using the difference of cubes formula: a^3 - b^3 = (a - b)(a^2 + ab + b^2). So, we have (x^3 - 1) = (x - 1)(x^2 + x + 1).
The denominator is a difference of squares: a^2 - b^2 = (a - b)(a + b). Therefore, (x^2 - 1) = (x - 1)(x + 1).
Now, we can simplify the expression by canceling out the common factors in the numerator and denominator:
[(x - 1)(x^2 + x + 1)] / [(x - 1)(x + 1)]
The (x - 1) terms cancel out, leaving us with:
x^2 + x + 1 / (x + 1)
So, the simplified form of the expression is (x^2 + x + 1) / (x + 1), which is not equal to x.
Know more about numerator here:
https://brainly.com/question/1217611
#SPJ8
in the pair of triangle, write the similarity statement and identify the postulate of theorem that justifies the similarity.
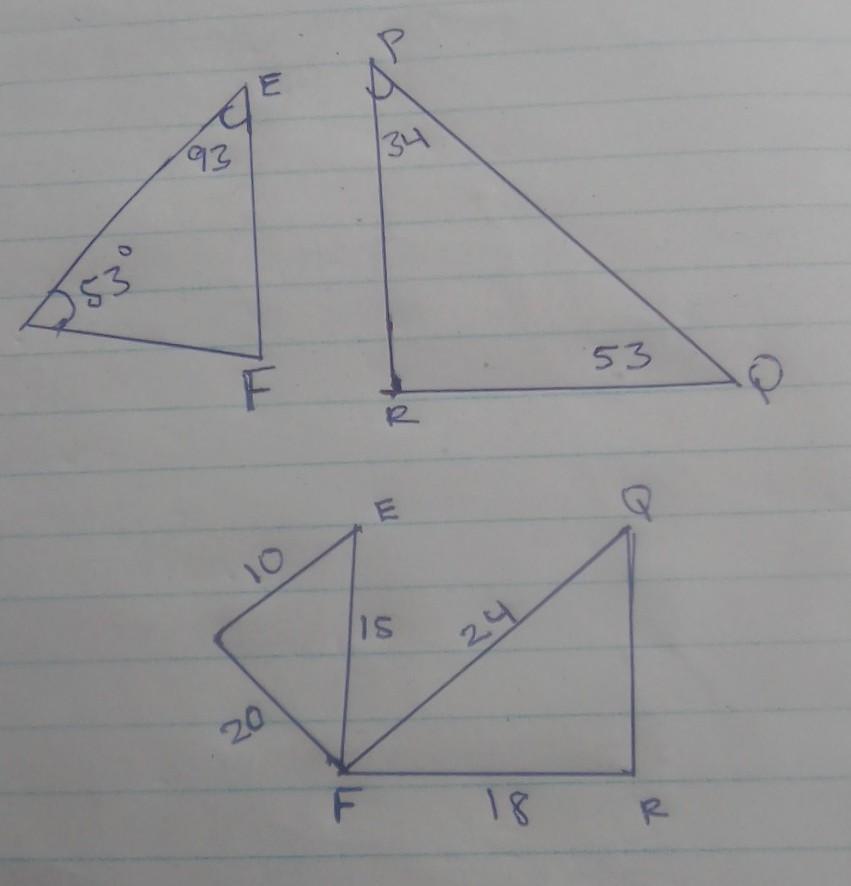
Answers
Answer:
ΔEFG ~ ΔRPQ - Angle Angle Angle Theorem
ΔEFG ~ ΔRFQ - Side Side Side Proportional Theorem
Step-by-step explanation:
First set : using triangle sum theory to find missing angle. Letters should match congruent angles when creating statement.
Second set :
\(\frac{EG}{RQ}\) = \(\frac{10}{12}\) = \(\frac{5}{6}\)
\(\frac{EF}{RF}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\)
\(\frac{FG}{FQ}\) = \(\frac{20}{24}\) = \(\frac{5}{6}\)
In the number 0.932, the value of the 3 is
3
.3
.03
.003
Please pick one of them?
Answers
.03
in 0.932, if you take away each number except 3, you'll be left with 0.030 or .03
Determine the mean, median, mode, and midrange for this collection of class test scores: 88 82 97 76 79 92 65 84 79 90 75 82 78 77 93 88 95 73 69 89 93 78 60 95 88 72 80 94 88 74 a. Mean is 84, median is 82, mode is 82, midrange is 77 b. Mean is 82, median is 88, mode is 88, midrange is 77 c. Mean is 82.4, median is 88, mode is 82, midrange is 78.5 d. Mean is 82.4, median is 82, mode is 88, midrange is 78.5
Answers
Mean of a given set of data = Sum of all observations ÷ Total number of observations
Mean of this data set = 88 + 82 + 97 + 76 + 79 + 92 + 65 + 84 + 79 + 90 + 75 + 82 + 78 + 77 + 93 + 88 + 95 + 73 + 69 89 + 93 + 78 + 60 + 95 + 88 + 72 + 80 + 94 + 88 + 74
Mean = 2729 ÷ 30
Mean = 82.4Median = the middle observation in a given set of data
Median of these test scores = 60 , 65 , 69 , 72 , 73 , 74 , 75 , 76 , 77 , 78 , 78 , 79 , 79 , 80 , 82 , 82 , 84 , 88 , 88 , 88 , 88 , 89 , 90 , 92 , 93 , 93 , 94 , 95 , 95 , 97 .
Median = 82 + 82 / 2
= 164 ÷ 2
= 82
Median = 82Mode = most frequently occurring number in a given set of data .
Mode of these test scores =
= 60 = 1 time
= 65 = 1 time
= 69 = 1 time
= 72 = 1 time
= 73 = 1 time
= 74 = 1 time
= 75 = 1 time
= 76 = 1 time
= 77 = 1 time
= 78 = 2 times
= 79 = 2 times
= 80 = 1 time
= 82 = 2 times
= 84 = 1 time
= 88 = 4 times
= 89 = 1 time
= 90 = 1 time
= 92 = 1 time
= 93 = 2 times
= 94 = 1 time
= 95 = 2 times
= 97 = 1 time
Mode = 88Midrange = average of the largest and smallest number in a given set of data
Midrange of these test scores = 97 + 60 / 2
= 97 + 60 / 2
= 157 ÷ 2
= 78.5
Midrange = 78.5Therefore , the correct option is :-
(d) Mean is 82.4 , median is 82 , mode is 88 , midrange is 78.530w-(w+6)-(5w+4)=-(5w+6)+(-8+3w) ayuda porfavor con esta ecuacion
Answers
Answer:
w=1/4
Step-by-step explanation:
30w-w-6-5w-4=5w+6-8+3w
24w-10=8w-2
24w-8w=-2+10
32w=8
w=1/4
At a swim meet, 8 different swimmers compete in the 800- meter freestyle race. How many different ways are there for these swimmers to finish
Answers
Using the arrangements formula, it is found that there are 40,320 ways for these swimmers to finish.
What is the arrangements formula?The number of possible arrangements of n elements is given by the factorial of n, that is:
\(A_n = n!\)
In this problem, there are n = 8 swimmers, hence they can finish arranged in 8! ways, that is:
\(A_8 = 8! = 40320\)
More can be learned about the arrangements formula at https://brainly.com/question/24648661
Find the indicated probability.
If P(A and B)=0.4, P(A) = 0.7, and
P(B) = 0.6, find P(A or B).
Answers
Answer:
P(A or B) = 0.9.
Step-by-step explanation:
This is a question of Venn probabilities.
We use the following relation to solve this question.
\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
The exercise states that:
\(P(A) = 0.7, P(B) = 0.6, P(A \cap B) = 0.4\)
Then
\(P(A \cup B) = P(A) + P(B) - P(A \cap B) = 0.7 + 0.6 - 0.4 = 0.9\)
The answer is:
P(A or B) = 0.9.
A person places $48800 in an investment account earning an annual rate of 3.1%,
compounded continuously. Using the formula V = Pert, where Vis the value of the
account in t years, P is the principal initially invested, e is the base of a natural
logarithm, and r is the rate of interest, determine the amount of money, to the
nearest cent, in the account after 13 years.
Answers
When a person places $48,800 in an investment account at an annual rate of 3.1% compounded continuously, using the formula, V = \(Pe^rt\), the amount of money (future value) after 13 years is $73,019.78.
What is compounding?Compounding refers to the process or interest system that computes periodic or continuous interest on both the principal and accumulated interest.
We can solve for the future value of an investment under continuous compounding using an online finance calculator as follows:
Using the formula V = \(Pe^rt\)
Principal (P) = $48,800.00
Annual Rate (R) = 3.1%
Compound (n) = Compounding Continuously
Time (t in years) = 13 years
Result:
V = $73,019.78
V = P + I where
P (principal) = $48,800.00
I (interest) = $24,219.78
Calculation Steps:
First, convert R as a percent to r as a decimal
r = R/100
r = 3.1/100
r = 0.031 rate per year,
Solving the equation for V:
V = \(Pe^rt\)
V = \(48,800.00(2.71828)^(0.031)(13)\)
V = $73,019.78
Learn more about continuous compounding at https://brainly.com/question/30460031.
#SPJ1
If electricity is billed at a rate of $0.75 per KWH and you used on average 120 KWHs per month, what would you expect to pay each month?
Answers
You would expect to pay $90 each month for electricity based on an average usage of 120 KWHs per month.
How to find the expected monthly payTo calculate the monthly cost of electricity, you can multiply the average number of kilowatt-hours (KWH) used per month by the cost per KWH.
Given:
Cost per KWH: $0.75
Average monthly usage: 120 KWHs
To find the monthly cost, you can multiply the cost per KWH by the average monthly usage:
Monthly Cost = Cost per KWH * Average monthly usage
Plugging in the values, we have:
Monthly Cost = $0.75/KWH * 120 KWHs
Calculating the result:
Monthly Cost = $90
Learn more about Monthly Cost at
https://brainly.com/question/24093839
#SPJ1
what is the value of x ?

Answers
Answer:
Since we know that the sum of the two angles equal 180, we can add them together to equal 180 degrees.
2x+10+x+26=180
Combine like terms.
3x+36=180
Subtract 36 from both sides.
3x=144
Divide 3 from both sides.
x=48
Hope this helps :)
Step-by-step explanation:
I hope this helps
Pls help, will give brainlist if u give me the answer!!
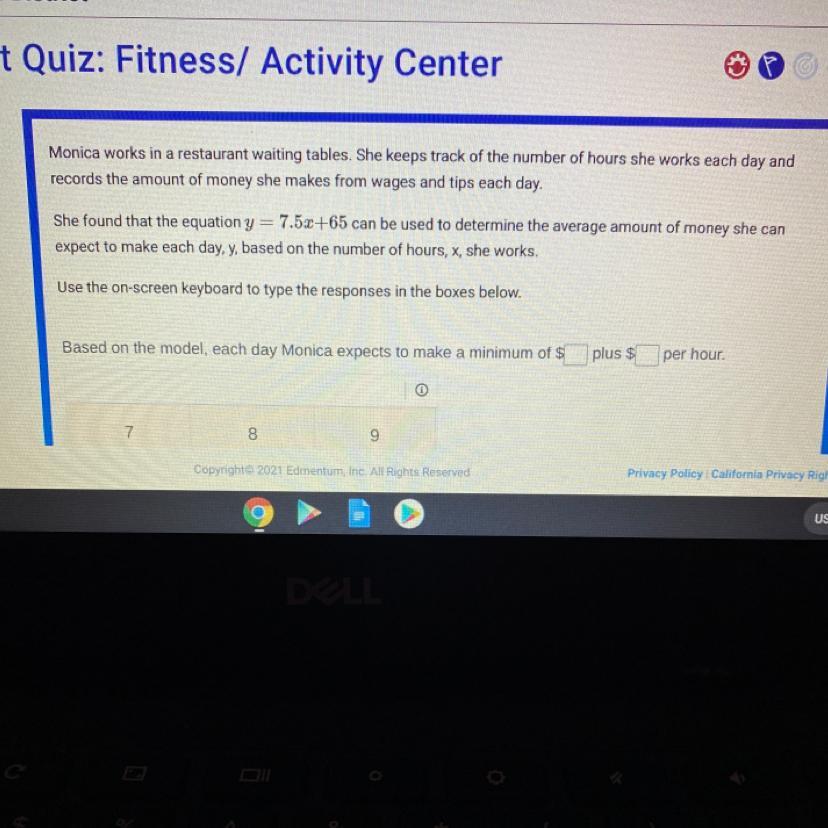
Answers
Answer:
$7.5 plus $65 per hour
Step-by-step explanation:
We are trying to find the minimum she can make in one day. The minimum amount of hours she can work is 1, so find y when x=1:
y=7.5x+65
y=7.5(1)+65
y=7.5+65
Need answer to this please

Answers
Answer:
I Think it's B 2/3
Tell me if i'm wrong
Graph the circle (x-2)^2 + (y-7)^2 = 4
Answers
Answer:
see attached
Step-by-step explanation:
You want the graph of the circle defined by the equation ...
(x-2)^2 + (y-7)^2 = 4.
Circle equationThe equation of a circle with center (h, k) and radius r is ...
(x -h)² +(y -k)² = r²
Comparing this to the given equation, we see ...
h = 2, k = 7, r² = 4
Then r = √4 = 2.
The circle will have its center at (2, 7) and will have a radius of 2. It is shown in the attached graph.
<95141404393>

What is the opposite reciprocal of 2/3?
Answers
Answer:The reciprocal of 2/3 is 3/2. The product of 2/3 and its reciprocal 3/2 is 1.
Step-by-step explanation:
9. Write the equation of the parabola in vertex form.
Vertex: (-4, 6); Point: (-2, -2)
Answers
Answer: y = − 2 ( x + 4 ) 2 + 6
Step-by-step explanation:
Find the parabola through ( − 2 , − 2 ) with vertex ( − 4 , 6 ) using the vertex form y = a ( x − h ) 2 + k .
Standard Form: y = − 2 x 2 − 16 x − 26
Vertex Form: y = − 2 ( x + 4 ) 2 + 6

Use implicit differentiation to find dy/dx and d^2y/dx^2.

Answers
Using implicit differentiation dy/dx = -(2x + y)/(x + 2y) and d2y/dx² = -2(x² - 3xy - y²)/(x + 2y)³.
Implicit differentiation is the process of differentiating an equation in which it is not easy or possible to express y explicitly in terms of x.
Given the equation x² + xy + y² = 5,
we can differentiate both sides with respect to x using the chain rule as follows:
2x + (x(dy/dx) + y) + 2y(dy/dx) = 0
Simplifying this equation yields:
(x + 2y)dy/dx = -(2x + y)
Hence, dy/dx = -(2x + y)/(x + 2y)
Next, we need to find d^2y/dx^2 by differentiating the expression for dy/dx obtained above with respect to x, using the quotient rule.
That is:
d/dx(dy/dx) = d/dx[-(2x + y)/(x + 2y)](x + 2y)d^2y/dx² - (2x + y)(d/dx(x + 2y))
= -(2x + y)(d/dx(x + 2y)) + (x + 2y)(d/dx(2x + y))
Simplifying this equation yields:
d2y/dx² = -2(x² - 3xy - y²)/(x + 2y)³
For more such questions on implicit differentiation visit:
https://brainly.com/question/25081524
#SPJ8
Please help!!!!!!!!!

Answers
The area of the triangle is 24 square meters
The area of the rectangle is 80 square meters.
24 + 80 = 104
A total of 627 tickets were sold for the school play. They were either adult tickets or student tickets. There were 73 fewer student tickets sold than adult tickets. How many adult tickets were sold?
Answers
Answer:
350
Step-by-step explanation:
Let "a" represent the number of adult tickets sold and "s" represent the number of student tickets sold. We can set up the following equation to represent the information given:
a + s = 627
s = a - 73
Substituting the second equation into the first equation gives us:
a + (a - 73) = 627
2a - 73 = 627
2a = 700
a = 350
Thus, there were 350 adult tickets sold.
Given 1 || m ||
|| n, find the value of x.
(x-6)⁰
60⁰
1
m
n

Answers
The value of x in the lines is 126 degree
We are given that;
Three parallel line and one intersecting line
Angles= (x-6) and 60
Now,
By supplementary angles property
Angle 1 + Angle 2 = 180 degree
Substituting the values of angles
x-6 + 60 = 180
x + 54 = 180
x = 180-54
x = 126
Therefore by supplementary angles answer will be 126 degree.
Learn more about supplementary angles here:
https://brainly.com/question/2882938
#SPJ1
The tables represent two linear functions in a system.
What is the solution to this system?
у
0 (43, -25)
0 - 14.-54]
O (-13, -50)
O (-14, -54)

Answers
hope that helps :)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
From left to right for the tables :
\(1) \: \: \: \: y = 4x + 2\)
And
\(2) \: \: \: \: y = 3x - 12\)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
To find the solution we need to take equal above equations .
\(4x + 2 = 3x - 12\)
Subtract sides 3x
\( - 3x + 4x + 2 = - 3x + 3x - 12 \\ \)
\(x + 2 = - 12\)
Subtract sides 2
\(x + 2 - 2 = - 12 - 2\)
\(x = - 14\)
Thus the x-coordinate of the solution must be -14 which is just in the last option.
Thus the correct answer is the last one.
Done...
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Out of 200 students in a senior class, 32 seniors are in the band and 64 seniors are in the band or on the honor roll. What is the probability that a randomly selected senior is both in the band and on the honor roll? Express your answer a fraction in simplest form.
Answers
The Probability that a randomly selected senior is both in the band and on the honor roll is 8/25.
To find the probability that a randomly selected senior is both in the band and on the honor roll, we need to divide the number of seniors who are in both categories by the total number of seniors.
Given:
Total number of seniors = 200
Number of seniors in the band = 32
Number of seniors in the band or on the honor roll = 64
Let's calculate the probability using these values:
Probability = Number of seniors in both categories / Total number of seniors
Probability = 64 / 200
To simplify this fraction, we can divide both the numerator and denominator by their greatest common divisor, which is 8:
Probability = (64 ÷ 8) / (200 ÷ 8)
Probability = 8 / 25
Therefore, the probability that a randomly selected senior is both in the band and on the honor roll is 8/25.
For more questions on Probability .
https://brainly.com/question/24756209
#SPJ8
