Is (8, –2) a solution to the equation y = 2?
Answers
Answer:
No
Step-by-step explanation:
Any point that aligns on the line of y = 2 is a solution. But (8, -2) falls below that line since the point's y-coordinate is equal to -2, not 2. Hope this helps!
Related Questions
Select all that apply
Which of the following name a line in the drawing ?

Answers
Answer:
I think FC but not sure
Step-by-step explanation:
the respn os that we looc at both sides f the line and see what the letters are
Answer:
DB
Step-by-step explanation:
just did it got it correct
See I’m in high school and my little sister needs help with this bc I’m in high school now and I forgot this stuff so please help my sisters with this 100 points

Answers
Answer:
1) S
2) U
3) K
4) B
5) Q
6) H
7) T
8) D
=
9) -6,-8
10) -8, 5
11) -3, -8
12) -5, 1
13) 5, -3
14) 7, -1
15) 7, 2
16) -7, 8
Step-by-step explanation:
1... 8. (x, y) coordinates given to point out letter
9... 16. given letter to point out (x, y) coordinates.
17.. 19.. 21.. 23.. see attached image

Answer:
1) S
2) U
3) K
4) B
5) Q
6) H
7) T
8) D
9) -6,-8
10) -8, 5
11) -3, -8
12) -5, 1
13) 5, -3
14) 7, -1
15) 7, 2
16) -7, 8
Rest I don't know dear
I hope it helps you
Mark me as the brainliest one pls
Thank you
From the simulation we learned that for a greater than alternative hypothesis, as the true mean gets farther away from the hypothesized value, the probability of a type ii error will?
Answers
As the true mean moves farther away from the hypothesized value, the probability of a Type II error decreases, leading to a higher probability of correctly detecting a true effect or difference.
As the true mean gets farther away from the hypothesized value in a hypothesis test, the probability of a Type II error (also known as a false negative) will decrease.
In a hypothesis test, the null hypothesis assumes that there is no significant difference or effect, while the alternative hypothesis suggests that there is a significant difference or effect.
A Type II error occurs when we fail to reject the null hypothesis when it is actually false. In other words, it is a failure to detect a true effect.
When the true mean is far away from the hypothesized value, the difference between the observed data and the hypothesized value becomes more pronounced.
This increases the likelihood of obtaining a test statistic that falls in the critical region (the region where we reject the null hypothesis). Consequently, the probability of correctly rejecting the null hypothesis (i.e., the probability of not making a Type II error) increases.
Learn more about probability here: https://brainly.com/question/32117953
#SPJ11
Formalize the following in terms of atomic propositions r, b, and w, first making clear how they correspond to the
English text. (a) Berries are ripe along the path, but rabbits have not been seen in the area.
(b) Rabbits have not been seen in the area, and walking on the path is safe, but berries are ripe along the path.
(c) If berries are ripe along the path, then walking is safe if and only if rabbits have not been seen in the area.
(d) It is not safe to walk along the path, but rabbits have not been seen in the area and the berries along the path are ripe.
e) For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to
pave been seen in the area.
Walking is not safe on the path whenever rabbits have been seen in the area and berries are ripe along the path.
Answers
Walking is not safe on the path whenever rabbits have been seen in the area, and berries are ripe along the path. This is formalized by using the →(if-then) and ∧(logical and) operators.
Given information and corresponding atomic propositions:
We need to formalize the given statements in terms of atomic propositions r, b, and w, which are defined as follows:
r: Rabbits have been seen in the area.
b: Berries are ripe along the path.
w: Walking on the path is safe.
Now, let us formalize each of the given statements in terms of these atomic propositions:
a) Berries are ripe along the path, but rabbits have not been seen in the area.
b: Rabbits have not been seen in the area, and walking on the path is safe, but berries are ripe along the path.
c: If berries are ripe along the path, then walking is safe if and only if rabbits have not been seen in the area.
d: It is not safe to walk along the path, but rabbits have not been seen in the area, and the berries along the path are ripe.
e) For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to have been seen in the area.
Walking is not safe on the path whenever rabbits have been seen in the area, and berries are ripe along the path.
The formalizations in terms of atomic propositions are:
a) b ∧ ¬r.b) ¬r ∧ w ∧
b.c) (b → w) ∧ (¬r → w).
d) ¬w ∧ ¬r ∧
b.e) (¬r ∧ ¬b) → w.b ∧
Berries are ripe along the path, but rabbits have not been seen in the area.
This is formalized by using the ∧(logical and) operator.
(¬r ∧ ¬b) → w: It means For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to have been seen in the area.
For more related questions on area:
https://brainly.com/question/1631786
#SPJ8
If y = 4 find slope, X-intercept and y-intercept.
Answers
Answer:
An equation in the form y = mx + b is in the 'slope y-intercept' form where m is the slope and b is the y-intercept. We can rewrite our equation, y = 4, in slope y-intercept form as follows: y = 0x + 4. Here, it is clear that the slope, or m, is zero. Therefore, the slope of the horizontal line y = 4 is zero
Chloe and eduardo are selling wrapping paper for a school fundraiser. customers can buy rolls of plain wrapping paper and rolls of holiday wrapping paper. chole sold 2 rolls of plain wrapping paper and 10 rolls of holiday wrapping paper for a total of $206. eduardo sold 3 rolls of plain wrapping paper and 5 rolls of holiday wrapping paper for a total of $129.
Answers
The cost of plain wrapping paper is $13 and the cost of holiday wrapping paper is $18
Chloe:
Number of plain wrapping paper sold = 2
Number of holiday wrapping paper sold = 10
Total income = $206
Eduardo:
Number of plain wrapping paper sold = 3
Number of holiday wrapping paper sold = 5
Total income = $129
Let x represent the cost of plain wrapping paper and y represent the cost of holiday wrapping paper:
Formulating the equations:
2x+10y = 206-----(1)
3x+5y = 129------(2)
Multiplying (2) with 2 and subtracting with (1) we get:
2x+10y = 206
6x+10y = 258
4x = 52
x = 13
So cost of plain wrapping paper is $13
holiday wrapping paper = $18
Learn more about linear equations:
https://brainly.com/question/13738061
#SPJ4
19.79 and 9.08 minutes Estimate the difference in their time?
Answers
The difference between 19.79 and 9.08 is found by subtracting the two numbers.
Hence,
\(19.79-9.08=10.71.\)The estimate of the difference is done in the following manner.
19.79 is close to 20 and 9.08 is close to 9; therefore, the easier subtraction we have to do is 20 - 9 = 11.

What greater 50% or 13/25
Answers
Answer: 13/25
Step-by-step explanation: it is equal to 52% which is greater than 50%
50% is greater than 13/25. To compare these two values, you can convert both of them to a common denominator, such as 50%. 50% is equal to 1/2, so 13/25 is equal to 52/50, which is less than 1/2 or 50%. Alternatively, you can also express both fractions as decimals and compare the two values that way. 50% is equal to 0.5, and 13/25 is equal to 0.52, so 50% is still greater than 13/25.
Solve the following equation for x = 5.

Answers
Answer: 5= 4x + 8
-8 -8
-3= 4x
the answer is x = 0.75
i don't know if I'm right if I am not I am sorry
bored hmu on twitter. handle is noclips_EMPTY
Also here is 20 points <3
Answers
Answer:
:)
Step-by-step explanation:
Answer:
nobody uses twitter anymore
Step-by-step explanation:
What is the area of this triangle? Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth.

Answers
Greetings from Brasil...
We need to use the Cosine Law in Any Triangle, so we can use Heron's formula.
AC² = AB² + BC² - 2.AB.BC.COS B
AC² = 11² + 9² - 2.11.9.COS 63
AC ≈ 10,63
Heron's Formula:
Area = √[P.(P - AB).(P - BC).(P - AC)]
where P = (AB + BC + AC)/2
P = (11 + 9 + 10,63)/2 ⇒ P ≈ 15,31
Area = √[15,31.(15,31 - 11).(15,31 - 9).(15,31 - 10,63)]
Area ≈ 44,21 u.a.
Find the slope of the line between (12,-18) and (-15,-18).
Answers
Answer:
The slope is 0
Step-by-step explanation:
The equation for slope is:
(y₂-y₁)/(x₂-x₁)
Now we plug in the coordinates into the equation:
(-18-(-18))/(-15-12)
(-18+18)/(-27)
0/-27
0
Answer:
0
Step-by-step explanation:
The slope formula is:
\(\frac{y_{1} -y_{2} }{x_{1}-x_{2} } \\\)
Let's substitute and solve:
\(\frac{-18-(-18)}{12-(-15)} = \frac{-18+18}{12+15} = \frac{0}{27} = 0\)
You just bought a 6-month straddle which pays the absolute difference between the stock price after 6 months and 42. Calculate the probability of having a positive profit after 6 months. Possible Answers A Less than 0.35 B At least 0.35 but less than 0.40 c At least 0.40 but less than 0.45 D At least 0.45 but less than 0.50 E At least 0.50
Answers
To calculate the probability of having a positive profit after 6 months, we need to consider two scenarios: the stock price being higher than 42 and the stock price being lower than 42.
If the stock price is higher than 42, then the profit will be the absolute difference between the stock price and 42. Let's call this difference "x". In this case, the profit will be x, since the call option will be in the money and the put option will be out of the money.
If the stock price is lower than 42, then the profit will be the absolute difference between 42 and the stock price. Let's call this difference "y". In this case, the profit will be y, since the put option will be in the money and the call option will be out of the money.
To calculate the probability of having a positive profit, we need to find the probability of the stock price being higher than 42, multiplied by the expected profit in that scenario, plus the probability of the stock price being lower than 42, multiplied by the expected profit in that scenario.
Let's assume that the stock price follows a normal distribution with a mean of 42 and a standard deviation of σ. The probability of the stock price being higher than 42 can be calculated as follows:
P(X > 42) = 1 - P(X < 42) = 1 - Φ((42 - 42)/σ) = 1 - Φ(0) = 0.5
Where Φ is the standard normal cumulative distribution function.
The expected profit in this scenario is x, which can be calculated as follows:
E(x) = ∫[42, +∞] x * f(x) dx
Where f(x) is the probability density function of the normal distribution.
Since the normal distribution is symmetric around the mean, we can assume that the expected profit in the lower scenario is the same as in the upper scenario, but with a negative sign:
E(y) = -E(x)
Therefore, the expected total profit is:
E(x+y) = E(x) + E(y) = 0
Since the expected total profit is zero, the probability of having a positive profit is the same as the probability of having a negative profit. Therefore, the answer is:
B At least 0.35 but less than 0.40
To answer your question, follow these steps:
Step 1: Understand the problem
You have bought a 6-month straddle that pays the absolute difference between the stock price after 6 months and 42. You need to calculate the probability of having a positive profit after 6 months.
Step 2: Identify the profit condition
For a positive profit, the payout should be greater than the cost of the straddle. Since we do not have the cost of the straddle, we cannot determine the exact probability of having a positive profit after 6 months.
However, we can infer that a higher probability of the stock price deviating significantly from 42 after 6 months will increase the likelihood of a positive profit. Unfortunately, without more information on the stock price distribution or the cost of the straddle, we cannot provide a definite answer within the given answer choices (A, B, C, D, or E).
To know more about the probability. Click on the link.
https://brainly.com/question/11234923
#SPJ11
Consider a standard normal random variable z. What is the value of z if the area to the right of z is 0.3336? Multiple Choice 0.43 0.52 O o 0.35 1.06 O
Answers
Looking up the value of 0.3336 in a standard normal distribution table, we find that the corresponding z-value is approximately 0.44.
Therefore, the answer is 0.43 (closest option).
Therefore, the value of z when the area to the right of z is 0.3336 is approximately 0.43.
Consider a standard normal random variable z. If the area to the right of z is 0.3336, the value of z can be found using the standard normal distribution table. The standard normal distribution table gives the area to the left of a given z-score. Since we are given the area to the right of z, we subtract 0.3336 from 1 to get the area to the left of z. This gives us an area of 0.6664 to the left of z on the standard normal distribution table. The closest value of z that corresponds to this area is 0.43. Therefore, the value of z when the area to the right of z is 0.3336 is approximately 0.43. The value of z, when the area to the right of z is 0.3336, is approximately 0.43.
Therefore, the value of z when the area to the right of z is 0.3336 is approximately 0.43.
To learn more about the mean and standard deviation visit:
brainly.com/question/475676
#SPJ11
In right triangle ABC, m∠B ≠ m∠C. Let sin B = r and cos B = s. What is sin C – cos C?
Answers
==================================================
Explanation:
We'll need these trig ratios
sine = opposite/hypotenusecosine = adjacent/hypotenuseRefer to the diagram below.
sin(B) = r = r/1 which tells us that the side opposite angle B is r units long. The hypotenuse is 1.
cos(B) = s = s/1 means the adjacent side to angle B is of length s
sides r and s are the two legs of the right triangle.
----------
From that diagram, we can then say:
sin(angle) = opposite/hypotenuse
sin(C) = s/1
sin(C) = s
This is identical to cos(B). We can say cos(B) = sin(C)
Also, we can say:
cos(angle) = adjacent/hypotenuse
cos(C) = r/1
cos(C) = r
So cos(C) = sin(B)
This works because B+C = 90
----------
So,
sin(C) - cos(C) = cos(B) - sin(B) = s - r

For each of the following pairs of numbers, find the gcd of the two numbers, and express the gcd as a linear combination of the two numbers.(a)56 and 42(b)81 and 60(c)259 and 77(d)72 and 42(e)80 and 61(f)630 and 147
Answers
The gcd of 630 and 147 can be expressed as 21 = (-3) x 630 + 13 x 147.
Here are the solutions for each pair of numbers:
(a) To find the gcd of 56 and 42, we can use the Euclidean algorithm:
56 = 42 x 1 + 14
42 = 14 x 3 + 0
So the gcd of 56 and 42 is 14. To express 14 as a linear combination of 56 and 42, we can use the extended Euclidean algorithm:
14 = 56 - 42 x 1
= (-1) x 56 + 1 x 42
So the gcd of 56 and 42 can be expressed as 14 = (-1) x 56 + 1 x 42.
(b) To find the gcd of 81 and 60, we can again use the Euclidean algorithm:
81 = 60 x 1 + 21
60 = 21 x 2 + 18
21 = 18 x 1 + 3
18 = 3 x 6 + 0
So the gcd of 81 and 60 is 3. To express 3 as a linear combination of 81 and 60, we can use the extended Euclidean algorithm:
3 = 21 - 18 x 1
= 21 - (60 - 21 x 2) x 1
= (-1) x 60 + 3 x 21
= (-1) x 60 + 3 x (81 - 60 x 1)
So the gcd of 81 and 60 can be expressed as 3 = (-1) x 60 + 3 x 81.
(c) To find the gcd of 259 and 77, we can use the Euclidean algorithm:
259 = 77 x 3 + 28
77 = 28 x 2 + 21
28 = 21 x 1 + 7
21 = 7 x 3 + 0
So the gcd of 259 and 77 is 7. To express 7 as a linear combination of 259 and 77, we can use the extended Euclidean algorithm:
7 = 28 - 21 x 1
= 28 - (77 - 28 x 2) x 1
= 3 x 28 - 77 x 1
= 3 x (259 - 77 x 3) - 77 x 1
So the gcd of 259 and 77 can be expressed as 7 = 3 x 259 - 10 x 77.
(d) To find the gcd of 72 and 42, we can use the Euclidean algorithm:
72 = 42 x 1 + 30
42 = 30 x 1 + 12
30 = 12 x 2 + 6
12 = 6 x 2 + 0
So the gcd of 72 and 42 is 6. To express 6 as a linear combination of 72 and 42, we can use the extended Euclidean algorithm:
6 = 42 - 30 x 1
= 42 - (72 - 42 x 1) x 1
= (-1) x 72 + 2 x 42
So the gcd of 72 and 42 can be expressed as 6 = (-1) x 72 + 2 x 42.
(e) To find the gcd of 80 and 61, we can use the Euclidean algorithm:
80 = 61 x 1 + 19
61 = 19 x 3 + 4
19 = 4 x 4 + 3
4 = 3 x 1 + 1
3 = 1 x 3 + 0
So the gcd of 80 and 61 is 1. To express 1 as a linear combination of 80 and 61, we can use the extended Euclidean algorithm:
1 = 19 - 4 x 3
= 19 - (61 - 19 x 3) x 3
= 10 x 19 - 3 x 61
= 10 x (80 - 61 x 1) - 3 x 61
So the gcd of 80 and 61 can be expressed as 1 = 10 x 80 - 13 x 61.
(f) To find the gcd of 630 and 147, we can use the Euclidean algorithm:
630 = 147 x 4 + 42
147 = 42 x 3 + 21
42 = 21 x 2 + 0
So the gcd of 630 and 147 is 21. To express 21 as a linear combination of 630 and 147, we can use the extended Euclidean algorithm:
21 = 147 - 42 x 3
= 147 - (630 - 147 x 4) x 3
= (-3) x 630 + 13 x 147
Learn more about Euclidean algorithm here:
https://brainly.com/question/13266751
#SPJ11
Select the figure that would be next in the pattern below.
1
3
6
10

Answers
Answer:
C)?
maybe....
im not sure!!
Find the lateral and total for the cone below. leave the answer in terms of pie.
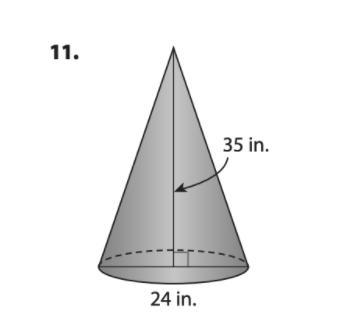
Answers
Answer:
35×24 = 840in²Step-by-step explanation:
height=35 in.base = 24in.then multiply
a^2-b^2+4b-4 please solve it step by step i will mark you brainlest
Answers
Answer:
b = a + 2 or b = 2 - a
Step-by-step explanation:
Solve for b:
-4 + a^2 + 4 b - b^2 = 0
The left hand side factors into a product with two terms:
(2 + a - b) (-2 + a + b) = 0
Split into two equations:
2 + a - b = 0 or -2 + a + b = 0
Subtract a + 2 from both sides:
-b = -a - 2 or -2 + a + b = 0
Multiply both sides by -1:
b = a + 2 or -2 + a + b = 0
Subtract a - 2 from both sides:
Answer:
b = a + 2 or b = 2 - a
find the pattern 7,10,14,19
Answers
Answer:
the answer is 25
Step-by-step explanation:
Rearrange the equation 4y - 8 = 12x + 4 into slope intercept form
Answers
Answer:
\(x = \frac{y}{3} - 1\)
Step-by-step explanation:
\(1. \: 4y - 8 - 4 = 12x \\ 2. \: 4y - 12 = 12x \\ 3. \: \frac{4y - 12}{12} = x \\ 4. \: \frac{4(y - 3)}{12} = x \\ 5. \: \frac{y - 3}{3} = x \\ 6. \: - 1 + \frac{y}{3} = x \\ 7. \: \frac{y}{3} -1 = x \\ 8. \: x = \frac{y}{3}-1\)
5. Find the area of the composite figure.
14 in.
12 in.
20 in.
10 in
(

Answers
Answer:
240 inch
Step-by-step explanation:

Help as soon as possible please. 20 points

Answers
there are 6 students in the class. one of them is to be selected as the best student and another student is to be selected as a runner-up. how many different ways can this be done?
Answers
If there are 6 students and one is selected for best student and another is selected for runner up, then 15 different ways that we can arrange the students
Total number of students in the class = 6 students
Number of students for best student = 1 student
Number of students for runner up = 1 students
Total number of students needed = 2
Here we have to use the combination
6\(C_2\) = 6! / 2!(6 - 2)!
= 6! / 2! × 4!
Split the terms and cancel it
= 6 × 5 / 2 × 1
Multiply the terms
= 30 / 2
Divide the numbers
= 15 combinations
Therefore, there are 15 combinations
Learn more about combination here
brainly.com/question/28720645
#SPJ4
Four cards are dealt at random without replacement from an ordinary deck of 52 cards. If it is known that the four cards have different face values, what is the probability that the first two cards are spades
Answers
Step-by-step explanation:
We gujra weeeeeeee
We gujra weeeeeeee
We gujra weeeeeeee
We gujra weeeeeeee
Use coordinate vectors to test the linear independence of the sets of polynomials. Explain your work.
(2-t)^3, (3-t)^2,1+6t-5t^2+t^3
Answers
The determinant of the matrix A is non-zero, the given set of polynomials is linearly independent.
To test the linear independence of the given set of polynomials {(2-t)^3, (3-t)^2, 1+6t-5t^2+t^3}, we will use coordinate vectors and perform the following steps:
1. Write the polynomials in the standard form:
(2-t)^3 = -t^3 + 6t^2 - 12t + 8
(3-t)^2 = t^2 - 6t + 9
1 + 6t - 5t^2 + t^3 = t^3 - 5t^2 + 6t + 1
2. Write the coordinate vectors for each polynomial:
v1 = (-1, 6, -12, 8)
v2 = (0, 1, -6, 9)
v3 = (1, -5, 6, 1)
3. Write the matrix A with these vectors as columns:
A = | -1 0 1 |
| 6 1 -5 |
| -12 -6 6 |
| 8 9 1 |
4. Find the determinant of the matrix A:
det(A) = -1 * (1 * (6 - 54) - (-5) * (-6 - 48)) - 0 * (...) + 1 * (6 * (...) - (-5) * (...))
det(A) = -1 * (-257) + 0 + 1 * (... - ...)
det(A) = 257
Since the determinant of the matrix A is non-zero, the given set of polynomials is linearly independent.
Learn more about linearly independent visit:
https://brainly.com/question/31086895
#SPJ11
PLEASE HELP IM CONFUSED

Answers
The cross section would be a circular sphere and a cylinder
What is a cylinder?A cylinder is defined as a shape that has there dimensional surface that is made up of two circles and a curved area.
The two flat circular bases are congruent to each other and It does not have any vertex.
A circular sphere is defined as a round object found in a space which is equally a three dimensional object.
Learn more about cylinder here:
https://brainly.com/question/27535498
#SPJ1
Peter wallpapered a wall that was 9 feet wide and 8 feet high. He had 27 square feet of wallpaper left over. How many square feet of wallpaper did he start with?
Answers
Answer:
99 square feet
Step-by-step explanation:
Because 8 times 9=72+27=99
Explanation:
1.) Find the area of the wall:
8 feet x 9 feet = 72 square feet
2.) To find out how many square feet of wallpaper he had at first, add the area of the wall to the wallpaper he has left:
72 square feet + 27 square feet = 99 ft2
SOMEBODY CORRECT ME IF IM WRONG
And if I am right (pls say if my answer was right after this) Mark me brainliest tysm!
Given m ||n, find the value of x.
+
(8x-7)
m
(9X-28)
Answers
Answer:
x = 21
Step-by-step explanation:
please help me idk what it's even asking for

Answers
Answer:
It is asking you what you would put as your statement for step 4.
Step-by-step explanation:
The answer by the way would be what you have clicked on - angle 1 + angle 4 = 180 degrees.
Answer:
marked answer is correct
Step-by-step explanation:
The problem is asking you to choose an equation that should be written as statement 4 of the proof.
Statement 4 is an algebraic expression of the verbal statement 3. The marked response is correct. It expresses the relationship that is the definition of supplementary angles.
__
Often you can gain a clue in these proofs by looking at places that use similar reasons or similar statements. Lines 5 and 6 are the algebraic and verbal representations of the relation between angles 1 and 2. This matches lines 3 and 4, which are the verbal and algebraic representation of the same relationship between angle 1 anf 4.