In reality, forecasts are typically not accurate. As such, it is typically most appropriate to use the std. deviation of demand as the primary measure of uncertainty. True/False
Answers
False. While it is true that forecasts can be subject to uncertainties and may not always be entirely accurate, it is not necessarily most appropriate to use the standard deviation of demand as the primary measure of uncertainty.
The standard deviation represents the dispersion of data points around the mean, and it is commonly used to measure variability within a dataset. However, it may not capture all the sources of uncertainty in demand forecasting.
Forecasts consider various factors such as historical data, market trends, customer behavior, and external influences to estimate future demand. Although they may not be entirely precise, they provide valuable insights and help organizations make informed decisions regarding production, inventory management, and resource allocation.
In addition to the standard deviation, other measures of uncertainty, such as confidence intervals or prediction intervals, can be used to quantify the range of possible outcomes and the associated level of uncertainty. These measures provide a more comprehensive understanding of the potential variations in demand, considering the inherent uncertainties in forecasting.
In conclusion, while forecasts may not always be completely accurate, they provide useful guidance for decision-making. The standard deviation of demand alone may not adequately capture the full range of uncertainties, and it is important to consider other measures of uncertainty when assessing the reliability and potential variations in demand forecasts.
Learn more about mean here: https://brainly.com/question/24182582
#SPJ11
Related Questions
describe in words where 35 would be plotted on the number line. between 5 and 6, but closer to 5 between 5 and 6, but closer to 6 between 6 and 7, but closer to 6 between 6 and 7, but closer to 7
Answers
According to the question 35 can be accurately placed between 5 and 6, but it is notably closer to 6 on the number line.
The number 35 would be plotted on the number line between 5 and 6, but closer to 6. When considering the interval between 5 and 6 as a whole, 35 falls closer to the 6 side. It is not exactly midway between the two numbers, but its proximity leans towards 6.
This positioning indicates that 35 aligns more closely with the value of 6 rather than 5. Visually, if we were to divide the distance between 5 and 6 into equal parts, the point representing 35 would be located at a distance closer to 6.
Therefore, 35 can be accurately placed between 5 and 6, but it is notably closer to 6 on the number line.
To know more about midway visit -
brainly.com/question/29503640
#SPJ11
WILL MARK BRAINLIEST
The number -2 is a solution to which of the following inequalities?
x + 7 > 5
-3 x 10
Answers
Answer:
-3 x 10
Step-by-step explanation:
the first one is 5
What is the value of the expression below? 2³(3³ – 6) +4 A. 214 B. 172 C. 28 D. 200
Answers
Answer:
The answer is C. 28
Im 96% sure
A teacher wants to arrange 16 chairs in equal rows in his classroom. How can he arrange the chairs? () in 4 rows, with 20 chairs in each row () in 2 rows, with 8 chairs in each row » In Brows, with 8 chairs in each row () in 3 rows, with 5 chairs in each row My Progress Sign out
Answers
Answer:
In 2 rows with 8 chairs in each row.
Step-by-step explanation:
2×8=16
The possible arrangement can be done as -
2 rows, with 8 chairs in each row.4 rows, with 4 chairs in each row.8 rows, with 2 chairs in each row.What is a Arrangement? What is equation modelling? What is a mathematical equation and expression?Arrangement numbers, more commonly called permutation numbers, or simply permutations, are the number of ways that a number of things can be ordered or arranged.Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.A mathematical expression is made up of terms (constants and variables) separated by mathematical operators.A mathematical equation is used to equate two expressions.Given is that a teacher wants to arrange 16 chairs in equal rows in his classroom.
The possible arrangement can be done as -
2 rows, with 8 chairs in each row.4 rows, with 4 chairs in each row.8 rows, with 2 chairs in each row.Therefore, the possible arrangement can be done as -
2 rows, with 8 chairs in each row.4 rows, with 4 chairs in each row.8 rows, with 2 chairs in each row.To solve more questions on equations, expressions and polynomials, visit the link below -
brainly.com/question/17421223
#SPJ2
A pool estimate that 43% of likely voters are in favor of additional restrictions on teen drivers the Poll has a margin of error of plus or minus 4%. Write and solve the absolute value equations to find the minimum and maximum percent of voters that support the restriction
Answers
Answer:
Kindly check explanation
Step-by-step explanation:
Given that :
Estimated number of voters in favor of additional restriction = 43%
Margin of Error = ±4%
Write and solve the absolute value equations to find the minimum and maximum percent of voters that support the restriction:
Minimum percentage of voters = 4% lesser than the estimated number of voters
Maximum percentage of voters = 4% greater than the estimated number of voters
Let number of voters = v
|v - 43%| = ±4%
v = - 4% + 43% = 39% = minimum percentage
v = +4% + 43% = 47% = maximum percentage
39% ≤ v ≤ 47%
Good Afternoon I am really stuck on this question whoever solves it I will give them brainliest with no unacceptable question thank you so much!

Answers
Answer:
Card picked=2
P(factors of 28)={1,2,4,7,14,28}
total cards=4
in percentage=4 x 20 + 20
80+20=100
Therefore 2 in percentage will be
2 x 20 + 20
=40+20=60%
traveling 1,200 mi in 4? unit rate
Answers
Answer:
300
Step-by-step explanation:
We divide the distance by time to get the rate. 1,200 is our distance, and 4 is our time.
1,200/4=300
Answer:
300 miles per hour
Explanation:
To find unit rate you have to divide the numerator by the denominator (miles/hours or 1,200/4 in this case). 1,200 divided by 4 is 300, so the answer is 300 miles per hour.
Solve for y in terms of v, w, x, and z.
wy=–zvx
Answers
Answer:
y = (-zvx)/w
........
determine which brands of orange juice people prefer. passerbys in a supermarket are asked to taste different brands without knowing which brand they are drinking, and which one they prefer. group of answer choices (a). experiment (b) observational study (c)unable to tell
Answers
The best way to determine which brands of orange juice people prefer is to conduct an experiment. In this experiment, passerbys in a supermarket are asked to taste different brands of orange juice without knowing which brand they are drinking, and which one they prefer.
After tasting each brand, they would be asked to indicate their preference. This type of experiment is known as a blind taste test. An observational study would not be effective in this situation, as it is unable to tell which brand people prefer.
The experiment and observational study are types of research. Observational research and experimental research are two methods of conducting research.
Observational research requires the researcher to observe participants in their natural setting, and experimental research requires the researcher to control the conditions and manipulate the independent variable. The experiment is a type of research in which the researcher manipulates one variable to determine if there is a causal relationship between the independent variable and the dependent variable.
The people at the supermarket who were asked to taste different brands of orange juice without knowing which brand they were drinking and which one they preferred are an example of an experiment.
This type of study is an example of a taste test experiment, which is a common technique used by food and drink manufacturers to determine which products consumers prefer.
To know more about experiment, refer here:
https://brainly.com/question/11256472#
#SPJ11
Which of the following correctly describes the domain of the function shown below?
Answers
Except than x = 1, all real numbers fall within the function's domain.
Why can't a domain consist entirely of real numbers?Since there are no limitations on what we can substitute for x, the domain of a function, f(x), is all real numbers because any real numbers would make f(x) a defined function. As a result, when this is not the case, the domain of a function, f(x), is not all real numbers.
The rational function r(x) = 2x/(x-1) is defined as follows.
So, we set the denominator to zero and solve for x in order to determine the domain of r(x):
x - 1 = 0
x = 1
Hence, x = 1 is the only value of x that causes the denominator to equal 0. R(x) therefore has a domain of all real numbers other than x = 1.
We can express the domain as follows in interval notation:
(-∞, 1) U (1, ∞)
Except than x = 1, all real numbers fall within the function's domain.
To know more about function visit:-
https://brainly.com/question/14830166
#SPJ1
Question:
Which of the following correctly describes the domain of the function shown below?
r(x) = 2x x-1
A. {x:x0}
B. {x: x = 1}
c. x all .real .numbers}
D. xx1}
I need alottttt of hellp

Answers
The expressions that have 3 as the greatest common factor are b + 3 + 6c, 27n + 66p, and 36 - 9j + 6k.
Thus,
b + 3 + 6c - Yes
-30 - 24z - No
27n + 66p - Yes
36 - 9j + 6k - Yes
Determining the greatest common factorFrom the question, we are to determine if 3 is the greatest common factor of the given expressions
b + 3 + 6c
3(b + 1 + 2c)
The greatest common factor is 3
-30 - 24z
6(-5 -4z)
The greatest common factor is not 3. The greatest common factor is 6
27n + 66p
3(9n + 22p)
The greatest common factor is 3
36 - 9j + 6k
3(12 - 3j + 2k)
Thus, The greatest common factor is 3
Learn more on Greatest common factor here: https://brainly.com/question/28180346
#SPJ1
(3ax + 4a) - (9x + 15a)
Answers
Answer:
3ax−11a−9x
Step-by-step explanation:
3ax+4a−(9x+15a)
Distribute the Negative Sign:
=3ax+4a+−1(9x+15a)
=3ax+4a+−1(9x)+−1(15a)
=3ax+4a+−9x+−15a
Combine Like Terms:
=3ax+4a+−9x+−15a
=(3ax)+(4a+−15a)+(−9x)
=3ax+−11a+−9x
y2-2y+6 for y=2is pls and the first will be the brainliest and I will follow them and give a like
Answers
Answer:
2*2-2*2+6
4-10
-6
Step-by-step explanation:
as we know that y=2 so i juat put the vakue of y
Answer:
put the value of 2 in the expression y2 and -2y
2sq.-2•2+6
4-4+6
0+6
6 ..
find a1 in a geometric series for which sn = 93, r = 2, and n = 5
Answers
The first term, a1, in the geometric series is -3.
What is Geometric Series?
A geometric series is a series for which the ratio of two consecutive terms is a constant function of the summation index. The more general case of a ratio and a rational sum-index function produces a series called a hypergeometric series. For the simplest case of a ratio equal to a constant, the terms have the form
To find the first term, a1, in a geometric series given the sum, Sn = 93, the common ratio, r = 2, and the number of terms, n = 5, we can use the formula for the sum of a geometric series:
Sn = a1 * (1 - r^n) / (1 - r)
Plugging in the given values, we have:
93 = a1 * (1 - 2^5) / (1 - 2)
Simplifying the expression:
93 = a1 * (1 - 32) / (-1)
93 = a1 * (-31)
Now we can solve for a1 by dividing both sides of the equation by -31:
a1 = 93 / -31
a1 = -3
Therefore, the first term, a1, in the geometric series is -3.
To learn more about Geometric Series from the given link
https://brainly.in/question/13322627
#SPJ4
Please I need help asap! A car rental company's standard charge includes an initial fee plus an additional fee for each mile driven. The standard charge (in dollars) is given by the function s=14.95+0.40M, where m is the number of miles driven. The company also offers an option to insure the car against damage. The insurance charge (in dollars) is given by the function i=5.80+0.25M. Let c be the total charge (in dollars) for a rental that includes insurance. Write an equation relating c to m. Simplify your answer as much as possible.
Answers
Answer:
a
Step-by-step explanation:
Which of the following numbers are less than -0.625
choose all that apply
A: - 8/5
B: -5/8
C:-0.5
Answers
Answer:
C
Step-by-step explanation:
C is the answer becuase it is a negative number less than -0.625
Suppose a random sample of eight students is chosen from the student body of a community college consisting of 40 % males. What is the probability that among the students in the sample no more than 7 are female ?
Answers
The probability that among the students in the sample no more than 7 are female is approximately 0.982 or 98.2%.
To calculate the probability that no more than 7 students in the sample are female, we need to consider the binomial distribution.
The community college student body consists of 40% males, which means 60% are females.
We have a random sample of 8 students.
To get the probability, we can use the binomial probability formula:
P(X ≤ k) = Σ (n choose x) * p^x * (1-p)^(n-x)
Where:
n is the number of trials (sample size)
k is the number of successes (female students)
p is the probability of success (proportion of females in the population)
(n choose x) is the binomial coefficient
In this case:
n = 8 (sample size)
p = 0.6 (proportion of females in the population)
k can take the values 0, 1, 2, 3, 4, 5, 6, or 7
We need to calculate the sum of probabilities for each value of k:
P(X ≤ 7) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7)
Calculating each term using the binomial probability formula and summing them will give us the desired probability.
Note: The binomial probability formula assumes independent and identically distributed (i.i.d.) trials and a fixed probability of success.
The community college student body consists of 40% males, which means 60% are females.
We have a random sample of 8 students.
Let's calculate the probability:
P(X ≤ 7) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7)
To calculate each term, we use the binomial probability formula:
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
Where:
n is the number of trials (sample size) = 8
k is the number of successes (female students)
p is the probability of success (proportion of females in the population) = 0.6
Let's calculate each term and sum them up:
P(X = 0) = (8 choose 0) * (0.6^0) * (0.4^8) = 0.1678
P(X = 1) = (8 choose 1) * (0.6^1) * (0.4^7) = 0.3579
P(X = 2) = (8 choose 2) * (0.6^2) * (0.4^6) = 0.3020
P(X = 3) = (8 choose 3) * (0.6^3) * (0.4^5) = 0.1463
P(X = 4) = (8 choose 4) * (0.6^4) * (0.4^4) = 0.0410
P(X = 5) = (8 choose 5) * (0.6^5) * (0.4^3) = 0.0068
P(X = 6) = (8 choose 6) * (0.6^6) * (0.4^2) = 0.0006
P(X = 7) = (8 choose 7) * (0.6^7) * (0.4^1) = 0.00003
Summing up the probabilities:
P(X ≤ 7) = 0.1678 + 0.3579 + 0.3020 + 0.1463 + 0.0410 + 0.0068 + 0.0006 + 0.00003 ≈ 0.982
Learn more about probability here, https://brainly.com/question/25839839
#SPJ11
Order of operations
1. 7 - 6 + 5
2. 31 + 19 - 8
3. 64 - 8 + 21
4. 17 + 34 - 2
5. 28 + (89-67)
6. ( 8 + 1 ) x 12 - 13
7. 63 divided by 9 + 8
8. 5 x 6 - (9 - 4)
9. 13 x 4 - 72 divided by 8
10. 16 divided by 2 + 8 x 3
11. 30 divided by ( 21 - 6) x 4
12. 6 x 7 divided by (6 + 8)
13. 88 - 16 x 5 + 2 - 3
14. (2+6) divided by 2 + 4 x 3
15. 4x4x4 - 24 divided by 8
16. I’m Done with
17. I’m Done with
18. 45 divided by 9 + 8 - 7 + 2 x 3
Answers
Step-by-step explanation:
I can help you this much....
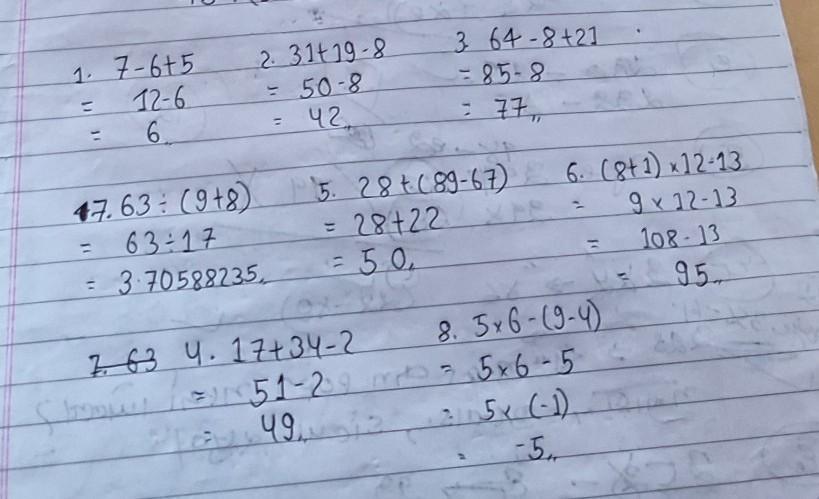
a fishing boat accidentally spills 15 barrels of diesel oil into the ocean. each barrel contains 42 gallons. if the oil film on the ocean is 2.5 x 102 nm thick, how much area in square meters will the oil slick cover? assume 1 gal
Answers
The area in square meters will the oil slick cover is 9.5×10⁶ m².
15 barrels of diesel spilt into the ocean, where each barrel contains 42 gallons. Thereby the total volume of the oil spilt by 15 barrels is calculated as follows:
The total volume of the oil spilt by 15 barrels = 15× 42 gallons.
=630 gallons
1 gallon = 3.78541 liters
Volume in L = 630 gallons × 3.78541 liters/ 1 gallon
= 2384.8083 L
1 L = 10⁻³ m³
2384.8083 L = 2384.8083 × 10⁻³ m³
= 2.3848083 m³
The area covered by the oil spill has to be determined, where the thickness of the oil spill is given to be 2.5×10² nm.
1 nm = 10⁻⁹ m
Thereby, 2.5×10² nm = 2.5×10²×10⁻⁹ m
= 2.5×10⁻⁷ m
Area (m²) = volume (m³)/thickness (m)
= 2.3848083 m³/ 2.5×10⁻⁷ m
= 0.95392×10⁷ m²
= 9.5×10⁶ m²
To know more about conversion factor, here
https://brainly.com/question/30166433
#SPJ4
Nine times the sum of a number and 8 equals 7.
Answers
Answer:
Step-by-step explanation:
9(x + 8) = 7
9x + 72 = 7
- 72
___________
- 65
\(\frac{9x}{9}\) = \(\frac{-65}{9}\)
= -7 \(\frac{2}{9}\)
A super train traveled 420 miles in 3 hours. If it maintain the same speed, how far could the train travel in 16 hours?
Answers
Answer:
We conclude that the train can travel 2240 miles in 16 hours.
Step-by-step explanation:
Given that a super train traveled 420 miles in 3 hours.
Distance covered = 420 milesTime taken = 3 hoursStep 1 of 2
Determine distance per hour
Important Tip:
The distance per hour can be determined by dividing the distance covered by the time taken.Distance per hour = Distance Covered / Time taken
= 420 / 3
= 140 miles per hour
Step 2 of 2
Determine the distance traveled in 16 hours
We already know that a super train travels 140 miles per hour. In other words, the speed of the super train is 140 miles per hour.
Important Tip:
To determine the distance covered in 16 hours, all we need to do is to multiply the distance covered per hour i.e. 140 with the total number of hours i.e. 16.Distance traveled in 16 hours = Distance per hour × 16
= 140 × 16
= 2240 miles
Conclusion:
Therefore, we conclude that the train can travel 2240 miles in 16 hours.
Is 0.75(repeating) rational or irrational?
Answers
Answer:rational
Step-by-step explanation:
Answer:
rational
Step-by-step explanation:
the event containing the outcomes belonging to a or b or both is the __________ of a and b.
Answers
The event containing the outcomes belonging to a or b or both is the union of a and b.
Let us consider two sets a and b, and say events or the elements in set a are: (x, y, z), and the elements in set b are: (o, p, q)
The union of these two sets will give:
aUb=(x, y, z, o, p, q)
Now, a union of two sets (denoted by U), for our case a and b, is the set or event containing the elements belonging to a or b or both the elements in a and b altogether.
Thus, the even containing the outcomes belonging to a or b or both in a and b altogether is the union of a and b.
Learn more about union of a set here:
https://brainly.com/question/23337676
#SPJ4
suppose abby tracks her travel time to work for 60 days and determines that her mean travel time, in minutes, is 35.6. assume the travel times are normally distributed with a standard deviation of 10.3 minutes. determine the travel time x such that 17.36% of the 60 days have a travel time that is at least x
Answers
The travel time x is 41.162 min such that 17.36% of the 60 days have a travel time that is at least x.
We have to determine the travel time such that 17.36% of the 60 days have a travel time that is at least.
Total work days to work = 60 days
The travel mean time = 35.6
Standard deviation = 10.3
For normal distribution,
P(X < A) = P(Z < (A - mean)/standard deviation)
P(X > x) = 0.2946
P(X < x) = 1 - 0.2946 = 0.7054
P(Z < (x - 35.6)/10.3) = 0.7054
Take the z value that corresponds to 0.7054 in the table of the standard normal distribution.
(x - 35.6)/10.3 = 0.54
x = 41.162 min
To learn more about standard normal distribution link is here
brainly.com/question/29509087
#SPJ4
Determine the unique solution of the following differential equations by using Laplace transforms: (1) y"(t) - 6y'(t) + 9y(t) = t^2e^3t if y'(O)=6 and y(0) = 2 (2) y"(t) + 2y'(t)- 3y (t) = e^-3t, if y(0) = 0 and y'(0)=0.
Answers
The unique solution of the following differential equations by using Laplace transforms,
(1) y(t) = 1/9 + 4/3t + 1/18\(e^{-3t}\) - 1/27t² - 1/54t\(e^{-3t}\)
(2) y(t) = (1/18)(\(e^{-3t}\) - 2t\(e^{-3t}\) - 3t + 2)
(1) To solve this differential equation using Laplace transforms, we first take the Laplace transform of both sides, using the fact that L{y'}=sY(s)-y(0) and L{y''}=s²Y(s)-sy(0)-y'(0):
s²Y(s) - 6sY(s) + 9Y(s) = (2/s³) - (6/s-3)³
Simplifying, we get:
Y(s) = (2/s^5) + (6/\((s-3)^4\)) / (s-3)²
Using partial fraction decomposition, we get:
Y(s) = (1/30s²) - (1/30s) + (1/18/(s-3)) - (1/90/(s-3)²) + (1/180/(s-3))
Taking the inverse Laplace transform of both sides, we get:
y(t) = (t²/30 - t/30) + (1/18)\(e^{(3t)}\) - (1/60)t \(e^{(3t)}\) + (1/360) t² \(e^{(3t)}\)
Therefore, the unique solution to the differential equation is:
y(t) = (t²/30 - t/30) + (1/18)\(e^{(3t)}\) - (1/60)t\(e^{(3t)}\) + (1/360) t²\(e^{(3t)}\)
(2) Following the same steps as above, we take the Laplace transform of both sides, using the fact that L{y'}=sY(s)-y(0) and L{y''}=s²Y(s)-sy(0)-y'(0):
s²Y(s) + 2sY(s) - 3Y(s) = 1/(s+3)
Simplifying, we get:
Y(s) = 1/(s+3) / (s+1)(s-3)
Using partial fraction decomposition, we get:
Y(s) = (-1/8/(s+1)) + (1/3/(s-3)) + (1/8/(s+3))
Taking the inverse Laplace transform of both sides, we get:
y(t) = (-1/8)\(e^{(-t)}\) + (1/3)\(e^{(3t)}\) + (1/8)\(e^{-3t}\)
Therefore, the unique solution to the differential equation is:
y(t) = (-1/8)\(e^{(-t)}\) + (1/3)\(e^{(3t)}\) + (1/8)\(e^{-3t}\)
Learn more about the Laplace transforms at
https://brainly.com/question/31481915
#SPJ4
HELP IM TIMED ROUND THE FACTOT AND ESTIMATE THE PRODUCT FOR EACH ONE

Answers
Answer:
The second one is 3,000 x 8,000 = 24,000,000 The first one is 700 x 100 = 70,000 then the third is 400 x 9,000 = 6,600,000 And the last is 9,000 x 57,000 = 513,000,000
Step-by-step explanation:
A box contains 2 purple marbles, 2 blue marbles, 3 green marbles, and 5 red marbles. 2 purple marbles, 2 blue marbles, 3 green marbles, and 5 red marbles. Which color marble is most likely to be picked? purple blue green red.
Answers
Answer:
the red marbles
Step-by-step explination:
Look below for work.
Specify the component functions of a vector field →F in R2 with the following property. →F is everywhere normal to the line x=2. Which of the following is one possible vector field →F ?
A. →F=(x,0)
B. →F=(−y,x)
C. →F=(x,y)
D. →F=(0,y)
Answers
Option D has a non-zero component function in the y-direction and a zero component function in the x-direction.
The vector field →F is normal to the line x=2, so it must be tangent to the line y-axis at every point. This means that the component function of →F in the x-direction should be 0 and the component function of →F in the y-direction should be non-zero.
Option D has a non-zero component function in the y-direction and a zero component function in the x-direction, so it satisfies the given property. Therefore, the answer is: D. →F=(0,y)
Learn more about y-direction here
https://brainly.com/question/14617282
#SPJ11
W X Y Z is a rhombus. If m

Answers
=====================================================
Explanation:
We can use the SSS congruence theorem to prove triangle WZX is congruent to triangle YZX. Then that leads to angle WZX = angle YZX.
In short, we've proven that ZX bisects angle WZY. Similarly, segment WY cuts angle XYZ in half. The proof is the same idea as mentioned in the first paragraph. For any rhombus, the diagonals always bisect the angles inside the rhombus.
Also, for any rhombus, the adjacent angles are supplementary.
So,
(angle WZY) + (angle XYZ) = 180
(angle WZY) + (136) = 180
angle WZY = 180 - 136
angle WZY = 44 degrees
Then we cut this in half to get the measure of angle XZY
angle XZY = (angle WZY)/2
angle XZY = (44)/2
angle XZY = 22 degrees
Set this equal to the 10x-8 expression and solve for x.
10x-8 = 22
10x = 22+8
10x = 30
x = 30/10
x = 3
\(3x - 1 \geqslant \frac{4x - 6}{2} \)
represent on a number line
Answers
Answer:[-2,+∝)
Step-by-step explanation:
we can multiply each side with 2,
2(3x-1)\(\geq\)2*((4x-6)/2)
6x-2\(\geq\)4x-6
6x-4x\(\geq\)-6+2
2x\(\geq\)-4
x\(\geq -2\)
[-2,+∝)