How does value of a affect the
parabola?
Answers
The parabola appears wider when |a| >1, the parabola appears thinner
When a is positive, the parabola opens upwards, but when a is negative parabola opens downwards
Step-by-step explanation:
brainliest?
Related Questions
A management consulting firm recommends that the ratio of middle-management salaries to management trainee salaries be 8:7. Using this recommendation, what is the annual middle-management salary if the annual management trainee salary is $17,000? (Round your answer to the nearest dollar.)
Answers
The management salary is $19,429
What is ratio?
Ratio is the quantitative relationship between two numbers which shows the number of times an amount or a number is contained within the other amount or number.
In this case, a ratio of 8:7 shows the number of times the management salaries is contained within the management trainee salary
The management salary has a value of 8 whereas the management trainee salary has a value of 7 as shown below:
salary ratio=management salary/management trainee salary
salary ratio=8/7
management salary=unknown(assume it is X)
management trainee salary=$17,000
8/7=X/$17,000
cross multiply
8*$17,000=7*X
X=8*$17,000/7
X=$19,429
The fact that annual management trainee salary is $17,000 means that the management salary is $19,429 annually.
Find out more about ratio on:https://brainly.com/question/2328454
#SPJ1
A sphere of radius r has surface area A=4πr
2
and volume V=(
3
4
)πr
3
. The radius of sphere 2 is double the radius of sphere 1 . (a) What is the ratio of the areas, A
2
/A
1
? (b) What is the ratio of the volumes, V
2
/V
1
? x
Answers
(a) The ratio of the areas, A2/A1, is: A2/A1 =\((16πr1^2)/(4πr1^2) = 4\)
(b) The ratio of the areas A2/A1 is 4, and the ratio of the volumes V2/V1 is 8.
(a) To find the ratio of the areas, A2/A1, we need to substitute the radii of sphere 2 and sphere 1 into the formula for surface area.
Let's denote the radius of sphere 1 as r1 and the radius of sphere 2 as r2, where r2 = 2r1.
For sphere 1:
A1 =\(4πr1^2\)
For sphere 2:
A2 = \(4πr2^2 = 4π(2r1)^2 = 4π(4r1^2) = 16πr1^2\)
Therefore, the ratio of the areas, A2/A1, is:
A2/A1 =\((16πr1^2)/(4πr1^2) = 4\)
(b) Similarly, to find the ratio of the volumes, V2/V1, we substitute the radii into the formula for volume.
For sphere 1:
V1 = \((4/3)πr1^3\)
For sphere 2:
V2 = \((4/3)πr2^3 = (4/3)π(2r1)^3 = (4/3)π(8r1^3) = (32/3)πr1^3\)
Therefore, the ratio of the volumes, V2/V1, is:
V2/V1 = \(((32/3)πr1^3)/((4/3)πr1^3) = 8\)
So, the ratio of the areas A2/A1 is 4, and the ratio of the volumes V2/V1 is 8.
Learn more about ratio here:
https://brainly.com/question/32531170
#SPJ11
Calculate the mode of the data set {5, 8, 2, 5, 11, 2, 5, 13}
PLS HELP

Answers
Answer:
5
Step-by-step explanation:
The mode is the most commonly occurring number in a set of numbers. In this one it is 5.
Circles of radii 3 and 6 are externally tangent to each other and are internally tangent to a circle of radius 9. The circle of radius 9 has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.
Answers
The square of the length of the chord that is a common external tangent of the other two circles with radii of 3 and 6 is 45.
Given that circles of radii 3 and 6 are externally tangent to each other and internally tangent to a circle of radius 9. The circle of radius 9 has a chord that serves as a common external tangent for the other two circles. The task is to find the square of the length of this chord.
The distance between the centers of the circles of radii 3 and 6 can be found by adding their radii: d1 = 3 + 6 = 9 units.
Since the circles are internally tangent to the circle of radius 9, the distance between their centers can be found by subtracting their radii from the radius of the larger circle: d2 = 9 - 3 - 6 = 0 units.
The chord is a common external tangent of the circles, and its length can be found by doubling the distance between the center of the circle of radius 9 and the chord: Chord length = 2 × h.
To find the height (h) of the triangle formed by the chord and the center of the circle of radius 9, we can use the formula h = (r1 + r2 - R) / 2, where r1 and r2 are the radii of the smaller circles, and R is the radius of the larger circle. In this case, h = (3 + 6 - 9) / 2 = 0.
Since h is zero, it means that the chord passes through the center of the circle of radius 9. Therefore, its length will be the diameter of the circle of radius 9.
The square of the length of the chord can be found using the Pythagorean theorem. Let's denote the length of the chord as d.
- We know that r1 + h = R, so h = R - r1 = 9 - 3 = 6.
- Using the Pythagorean theorem: d = sqrt(R² - h²) = √(9² - 6²) = √(81 - 36) = √(45).
Therefore, the square of the length of the chord is d^2 = 45.
In summary, the square of the length of the chord that serves as a common external tangent for the circles of radii 3 and 6, and is internally tangent to a circle of radius 9, is 45.
To know more about circle, click here
https://brainly.com/question/15424530
#SPJ11
I NEED HELP ON THIS ASAP! IT'S DUE TODAY!!!


Answers
Answer:
b = 8.485
c = 23.995 ≈ 24
Step-by-step explanation:
Part b:
\(\sqrt{(10-4)^2+(9-3)^2}\)
√(36 + 36)
= 8.485
Part c:
Base = \(\sqrt{(6-2)^2+(1-5)^2}\)
Base = 5.656
Area = Base x Height x 0.5
Area = 5.656 x 8.485 x 0.5
Area = 23.995 ≈ 24
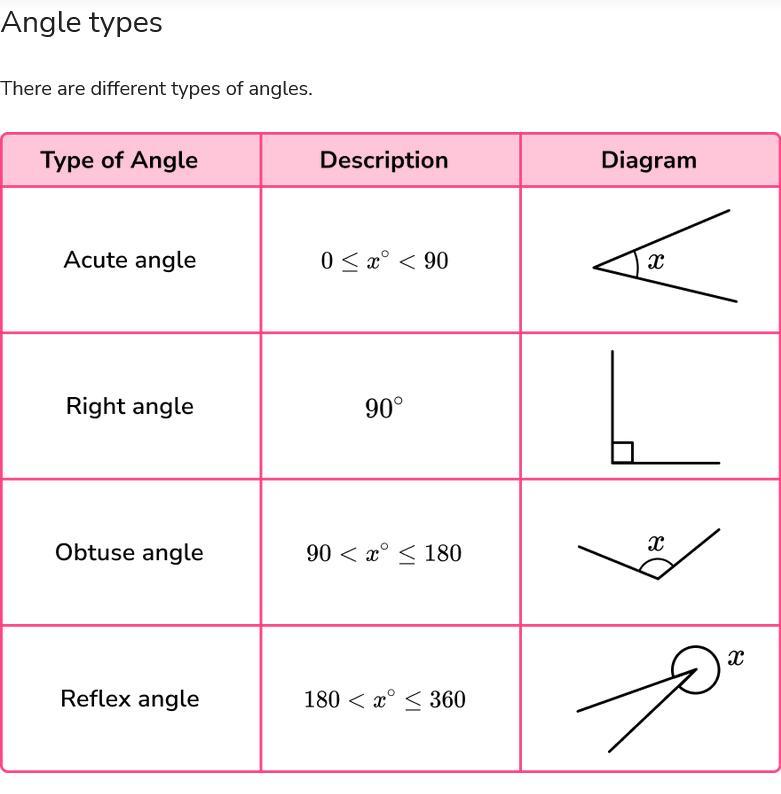
Hi I’m in fourth grade and I need help about angles can you please help me
Answers
Answer:pl z give me brainliest the crown next to the stars when two people answer :) have a good day ;)
Step-by-step explanation:
hope this helped
A geologist visits 20 volcanoes in Alaska and California.
What if 60% of the volcanoes were in California? How many volcanoes would the geologist have visited in California and how many in Alaska?
Answers
Answer:
60% of 20 is 12
40% of 20 is 8
12 in California
8 in Alaska
Which value of W makes 14=11+ w/8•6 a true statement
Answers
Answer:
w = 144
Step-by-step explanation:
11 + w/8*6 = 14
w/8*6 = 3
w/48 = 3
w = 144
Contamination is a problem in the manufacture of optical storage disks. The number of particles of contamination that occur on an optical disk has a Poisson distribution, and the average number of particles per square centimeter of media surface is 0.1. The area of a disk under study is 100 cm2. Find the probability more than 12 particles occur in the area of a disk under study.
Answers
The probability that more than 12 particles occur in the area of a disk under the study is 0.20844.
The number of particles follows a Poisson Distribution.
A Poisson Distribution over a variable X, having a mean λ, has a probability for a random variable x as \(P(X = x) = e^{-\lambda} \frac{\lambda^{x}}{x!}\) .
In the question, x = 12.
λ = 100*0.1 = 10.
To find : P(X > 12)
P(X > 12) = 1 - P(X ≤ 12) = 1 - poissoncdf(10,12)
As to find the probability of a Poisson Distribution P(X ≤ x), for a mean = λ, we use the calculator function poissoncdf(λ,x).
Therefore, P(X > 12) = 1 - 0.79156 = 0.20844.
Therefore, the probability that more than 12 particles occur in the area of a disk under the study is 0.20844.
Learn more about the Poisson Distribution at
https://brainly.com/question/7879375
#SPJ4
18x + 3y = -21 slope intercept form
Answers
Answer: y=-6x-7
Step-by-step explanation:
Slope-intercept form is y=mx+b. This means, we want to isolate y.
18x+3y=-21 [subtract both sides by 18x]
3y=-18x-21 [divide both sides by 3]
y=-6x-7
Now, our equation is in slope-intercept form.
Please help this is due in 30 mins

Answers
Answer:
im pretty sure its c or rotation
Step-by-step explanation:
Suppose that BC financial aid alots a textbook stipend by claiming that the average textbook at BC bookstore costs $$ 76. You want to test this claim.
Based on a sample of 170 textbooks at the store, you find an average of 80.2 and a standard deviation of 14.2.
The Point estimate is(to 3 decimals):
The 95 % confidence interval (use z*) is(to 3 decimals):
Answers
the 95% confidence interval for the average textbook cost at the BC bookstore is approximately $77.76 to $82.64.
The point estimate for the average textbook cost at the BC bookstore is the sample mean, which is 80.2. Therefore, the point estimate is 80.2 (to 3 decimals).
To calculate the 95% confidence interval, we need to determine the margin of error and then construct the interval using the sample mean, the margin of error, and the appropriate critical value based on the standard normal distribution.
The margin of error can be calculated using the formula:
Margin of Error = z * (standard deviation / sqrt(sample size))
Given that the sample size is 170, the standard deviation is 14.2, and we want a 95% confidence interval, we need to find the corresponding critical value, denoted as z*.
The critical value for a 95% confidence interval is found by subtracting half of the confidence level (0.05) from 1 and then finding the z-score associated with that cumulative probability. Looking up the value in a standard normal distribution table, we find that the z-score is approximately 1.96.
Now, we can calculate the margin of error:
Margin of Error = 1.96 * (14.2 / sqrt(170))
Margin of Error ≈ 2.44 (to 3 decimals)
Finally, we can construct the 95% confidence interval using the sample mean and the margin of error:
95% Confidence Interval = (Sample Mean - Margin of Error, Sample Mean + Margin of Error)
95% Confidence Interval = (80.2 - 2.44, 80.2 + 2.44)
95% Confidence Interval ≈ (77.76, 82.64) (to 3 decimals)
To know more about interval visit:
brainly.com/question/11051767
#SPJ11
i need this done quick!! help!!1!!!1

Answers
Answer:
113.1 inches squared
Step-by-step explanation:
Answer:
the answer is 113.1
Step-by-step explanation:
given
d=12
diameter is half of the radius
so
r=6
now we apply the formula
A=22/7 × 6×6
=792/7
=113.1
i hope the answer is right
PLEASE HELP I WILL MARK BRAINLIEST

Answers
Hope this helps :)
(Would love brainliest)
You must decide whether to buy new machinery to produce product X or to modify existing machinery. You believe the probability of a prosperous economy next year is 0.7. Prepare a decision tree and use it to calculate the expected value of the buy new option. The payoff table is provided below (+ for profits and - for losses).
When entering the answer, do not use the $ symbol. Do not enter the thousand separator. Enter up to 2 decimal places after the decimal point. For example, $6,525.35 must be entered as 6525.35
N1: Prosperity ($) N2: Recession ($)
A1 (Buy New) $1,035,332 $-150,000
A2(Modify) $823,625 $293,648
Answers
The expected value of the "Buy New" option is 724732.60.
Decision Tree:
To solve the given problem, the first step is to create a decision tree. The decision tree for the given problem is shown below:
Expected Value Calculation: The expected value of the "Buy New" option can be calculated using the following formula:
Expected Value = (Prob. of Prosperity * Payoff for Prosperity) + (Prob. of Recession * Payoff for Recession)
Substituting the given values in the above formula, we get:
Expected Value for "Buy New" = (0.7 * 1,035,332) + (0.3 * -150,000)Expected Value for "Buy New" = 724,732.60
Therefore, the expected value of the "Buy New" option is 724,732.60.
Conclusion:
To conclude, the decision tree is an effective tool used in decision making, especially when the consequences of different decisions are unclear. It helps individuals understand the costs and benefits of different choices and decide the best possible action based on their preferences and probabilities.
The expected value of the "Buy New" option is 724,732.60.
For more questions on expected value
https://brainly.com/question/14723169
#SPJ8
what is the relative frequency of students speaking spanish?

Answers
Answer:
Step-by-step explanation:
add all of them up, Julie, 6 + 12 + 3 + 4 = 25
there are 25 total students. now divide each of the number of people that speak that language by the total students
6/25 = .24 = 24%
12/25= .45 = 48%
3/25 = .12 = 12%
4/25 = .16 = 16%
Also, if you want to just check, see if the percentages add to 100%
Using the relative frequency concept, it is found that the relative frequencies for students speaking each language is:
Arabic: 0.24Spanish: 0.48German: 0.12Vietnamese: 0.16--------------------------------
A relative frequency of a to b is a/b, that is, the number of desired outcomes divided by the number of total outcomes.
--------------------------------
6 + 12 + 3 + 4 = 25 students.6 speak Arabic, thus, the relative frequency of students speaking Arabic is 6/25 = 0.24.12 speak Spanish, thus, the relative frequency of students speaking Spanish is 12/25 = 0.48.3 speak German, thus, the relative frequency of students speaking German is 3/25 = 0.12.4 speak Vietnamese, thus, the relative frequency of students speaking Vietnamese is 4/25 = 0.16.A similar question is given at https://brainly.com/question/20630951
Is the ordered pair (-6,3) a solution of the inequality -4x - 8y < 15 ?
A) Yes, the ordered pair is a solution
B) No, the ordered pair is not a solution.
Answers
Given:
The inequality is:
\(-4x-7y<15\)
To find:
The whether (-6,3) is a solution of given inequality of not.
Solution:
We have,
\(-4x-7y<15\)
We need to check the inequality for point (-6,3).
Substitute \(x=-6, y=3\) in the given inequality.
\(-4(-6)-7(3)<15\)
\(24-21<15\)
\(3<15\)
This statement is true. It means the point (-6,3) satisfies the given inequality.
Therefore, the correct option is A. Yes, the ordered pair is a solution.
Convert the rectangle coordinates to polar coordinates where r > 0
and 0 ≤ 2 . and Convert the polar coordinates to rectangular coordinates.
please list steps on how to solve so I can solve these in the future

Answers
Answer:
(1) - C, \((3,\frac{\pi}{6})\)
(2) - B, \((0,-2)\)
Step-by-step explanation:
\(\text{Using the following conversions:}\\\boxed{\left\begin{array}{ccc}\text{\underline{Rect. to Polar:}}\\(x,y)\rightarrow(r, \theta)\\\\r=\sqrt{x^2+y^2}\\\\\theta=\tan^{-1}(\frac{y}{x})\end{array}\right} \ \ \boxed{\left\begin{array}{ccc}\text{\underline{Polar to Rect.:}}\\(r, \theta)\rightarrow(x,y)\\\\x=r\cos \theta\\\\y=r \sin\theta\end{array}\right}\)
Note that when doing these calculations, make sure your calculator is in radians mode.
Question #2:
Given:
\((\frac{3\sqrt{3} }{2} ,\frac{3}{2} ) \ \text{in} \ (x,y)\)
\((\frac{3\sqrt{3} }{2} ,\frac{3}{2} )\\\\\Rightarrow r=\sqrt{(\frac{2\sqrt{2} }{2})^2+(\frac{3}{2})^2} \\\\\Longrightarrow r=\sqrt{\frac{27}{4} +\frac{9}{4} } \\\\\Longrightarrow r=\sqrt{9}\\\\\therefore \boxed{ r=3}\\\\\Rightarrow \theta=\tan^{-1}(\frac{\frac{3}{2}}{\frac{3\sqrt{3} }{2}})\\\\\Longrightarrow \theta=\tan^{-1}(\frac{\sqrt{3} }{3})\\\therefore \boxed{\theta=\frac{\pi}{6} }\)
Thus, the correct option is C.
\(\boxed{\boxed{(3,\frac{\pi}{6})}}\)
Question #3:
Given:
\((2,\frac{3\pi}{2} ) \ \text{in} \ (r,\theta)\)
\((2,\frac{3\pi}{2} ) \\\\\Rightarrow x=(2)\cos(\frac{3\pi}{2})\\\\\Longrightarrow x=(2)(0)\\\\\therefore \boxed{x=0}\\\\\Rightarrow y=(2)\sin(\frac{3\pi}{2})\\\\Longrightarrow y=(2)(-1)\\\\\therefore \boxed{y=-2}\)
Thus, the correct option is B.
\(\boxed{\boxed{(0,-2)}}\)
cual es la propiedad distributiva de la multiplicacion 72x(54+27)
Answers
Answer:
5832
Step-by-step explanation:
54+27=81x72=5832
Which of the following is basically a promissory note, or a promise to repay a certain amount of money at some point in the future?
-Bond
-CD
-Mutual fund
-Stock
Answers
Answer:
Bond
Step-by-step explanation:
A promissory note or a promise to repay a certain amount of money at some point in the future is basically a bond.
A bond is a debt security that represents a loan made by an investor to a borrower, which is usually a corporation or government agency. It is a fixed-income investment, meaning that the borrower promises to pay a specific amount of interest over a set period of time and return the principal amount of the loan on the date of maturity. Bonds are issued for various purposes, such as raising capital, funding new projects, or refinancing debt.
CD (Certificate of Deposit) is a savings instrument issued by a bank or credit union that generally pays a fixed rate of interest over a set term. Mutual fund is an investment vehicle that pools money from multiple investors to purchase a portfolio of securities, such as stocks, bonds, or both. Stock is an ownership share in a company that represents a claim on part of the company's assets and earnings.
Pea aphids, Acyrthosiphon pisum, are small, wingless, sapsucking insects that live on plants. They evade predators (such as ladybugs) by dropping off. A study examined the mechanism of aphid drops. Researchers placed aphids on a leaf positioned at four different heights (in centimeters, cm) above a surface covered with petroleum jelly. When a ladybug was introduced, the aphids dropped, and the petroleum jelly helped capture their landing posture (upright or not). Each aphid performed this experiment only once. The findings are given in the table. Dropping Hcight Landing Posture3 cm 5 cm10 cm20cm Upright Not upright Sample size 20 23 10 30 30 27 29 30 30 To access the complete data set, click the link for your preferred software format: Excel Minitab JMP SPSS TI R Mac-TXT PC-TXT CSV CrunchIt! The null hypothesis "no relationship" says that in the population of aphids, the proportions that land upright are the same when the dropping height is 3, 5, 10, and 20 cm. The two-way table contains expected cell counts if this hypothesis is true Landing Posture 3 cm5 cm10 cm 20 cm Total 24.75 24.75 24.75 24.75 99 Not upright 5.255.255.255.255.25 30 30 30 30 30 Upright Total (a) Use the tables to calculate the value of the chi-square statistic. (Enter your answer rounded to three decimal places.) 223.359 Question Source Baldi4e- The Practice Of Statistics In The Life Sciences Publisher: W.H. Freeman
Answers
The value of chi-square statistic (\(X^{2}\)) is 11.26
As per the given question
the sample space of all the four cases are 30
the proportions that land upright are the same when the dropping height is 3, 5, 10, and 20 cm.
the formula of chi-squared test is
\(X^2=\sum\frac{(O_i-E_i)^2}{E}\)
where
\(X^{2}\) is chi-square
\(O_i\) is the observed value
\(E_i\) is the expected value
the upright observed value are 20,23,27,29
the upright expected values are 24.75
now
the chi-square at 3cm height is
\(X^2=\(\frac{(20-24.75)^2}{24.75}\)
=> \(X^2=0.91\)
the chi- square at 5cm height is
\(X^2=\(\frac{(23-24.75)^2}{24.75}\)
=> \(X^2=0.12\)
the value of chi-square at 10cm is
\(X^2=\(\frac{(27-24.75)^2}{24.75}\)
=>\(X^2=0.20\)
the value of chi-square at 20cm is
\(X^2=\(\frac{(29-24.75)^2}{24.75}\)
=> \(X^2=1.97\)
the not upright observed values are
10,7,3,1
the not upright expected values are 5.25
the chi-square test at 3cm height is
\(X^2=\(\frac{(10-5.25)^2}{5.25}\)
=> \(X^2=4.30\)
the chi-square test at 5cm height is
\(X^2=\(\frac{(7-5.25)^2}{5.25}\)
=> \(X^2=0.58\)
the chi-square test at 10cm height is
\(X^2=\(\frac{(3-5.25)^2}{5.25}\)
=> \(X^2=0.96\)
the chi-square test at 20 cm is
\(X^2=\(\frac{(1-5.25)^2}{5.25}\)
=> \(X^2=3.44\)
now,
the total
chi-square value at 3cm height is
=>X^2=0.91+4.30
=> \(X^{2}\)= 5.21
chi-square at 5cm height is
=> \(X^{2}=0.12+0.58\)
=> \(X^2=0.71\)
chi-square at 10cm is
=> \(X^{2}=0.20+096\)
=> \(X^2=1.16\)
chi-square at 20 cm is
=> \(X^{2}=0.73+3.44\)
=> \(X^{2}=4.17\)
now ,
the total chi-square statistic is
=>\(X^{2}=\)5.21+0.71+1.17+4.17
=>\(X^{2}=\) 11.26
To learn more about chi- square statistic:
https://brainly.com/question/28284014
#SPJ4
The radius of a circle is 6 inches. What is the area of a sector bounded by a central angle measuring 120°
Answers
Knowing that a circle has a radius of 6 inches, the area of a sector with a central angle of 120º is 12π square inches.
The area of a sector can be found using the formula:
Area of sector = (Central angle/360°) × π × r²
Where "central angle" is the angle of the sector in degrees and "r" is the radius of the circle.
In this case, the central angle is 120° and the radius is 6 inches. Plugging these values into the formula, we get:
Area of sector = (120°/360°) × π × 6²
Area of sector = (1/3) × π × 36
Area of sector = 12π square inches
Therefore, the area of the sector bounded by a central angle measuring 120° in a circle with a radius of 6 inches is 12π square inches.
See more about central angle at https://brainly.com/question/10945528.
#SPJ11
5. Oshaunda buys a car that costs $21,000. It depreciates at 8.2% per year. a. Write an equation for the value of the car. V=21,000(1-0.082) V-21,000(0.918) B. Oshaunda tries to sell the car 4 years later. What is the car worth when it is 4 years old? Hint: Use your formula for part (a), and plug in t = 4. Use GEMA to finish the math.
Answers
Answer:
a.
\(f(t) = 21000( {.918}^{t} )\)
b.
\(f(4) = 21000( {.918}^{4}) = 14913.86\)
Which exrpression is equivalent using the distributive property to: 3(4x + 5y)?

Answers
Answer:
\( \sf \: c) \: 3(4x) + 3(5y) \)
Step-by-step explanation:
Now we have to,
→ find the equivalent expression.
The expression is,
→ 3(4x + 5y)
Let's solve the problem,
→ 3(4x + 5y)
→ (3 × 4x) + (3 × 5y)
→ 3(4x) + 3(5y)
Hence, option (c) is correct.
0.4141 rounded to the nearest thousandth
Answers
Answer:
0.4141 rounded to the nearest thousandth is 0.414.
Step-by-step explanation:
Since the number is 0.4141, and the number following the thousandths place is under 5, the thousandth place stays the same. If it were 5 or over, it would round up making it 0.415, but it's not so it is 0.414.
Find the 21st term of the sequence 15,8,1,-6
Answers
Answer:
-125
Step-by-step explanation:
Each term is 7 less than the previous term.
1st term: 15
2nd term: 15 - 7
3rd term: 15 - 7 - 7 = 15 - 2(7)
4th term = 15 - 7 - 7 - 7 = 15 - 3(7)
Notice that each term is 15 minus a multiple of 7. The multiple is obtained by multiplying 7 by 1 less than the term number.
The formula is:
\( a_n = 15 - 7(n - 1) \)
For the 21st term, multiply 7 by 20, and subtract from 15.
7 × 20 = 140
15 - 140 = -125
Using the formula:
\( a_{21} = 15 - 7(21 - 1) = 15 - 7(20) = 15 - 140 = -125 \)
Answer: -125
The major difference between temperate rainforests and tropical rainforests is that
A.
the rainfall of temperate rainforests is generally higher than that of tropical rainforests.
B.
the temperatures of temperate rainforests are generally higher than those of tropical rainforests.
C.
the temperatures of temperate rainforests are generally lower than those of tropical rainforests.
D.
the rainfall of temperate rainforests is generally lower than that of tropical rainforests.
Answers
Answer:
C.
the temperatures of temperate rainforests are generally lower than those of tropical rainforests.
find the radius of convergence, r, of the series. [infinity] (−1)n xn 2n ln(n) n = 2 r = incorrect: your answer is incorrect.
Answers
The radius of convergence, r, is 2. The series converges for values of x within the interval (-2, 2).
To find the radius of convergence, we can use the ratio test. Consider the series:
∑ (-1)^n * (x^n) / (2^n * ln(n))
Applying the ratio test:
lim |(-1)^(n+1) * (x^(n+1)) / (2^(n+1) * ln(n+1))| / |(-1)^n * (x^n) / (2^n * ln(n))|
= lim |x / 2 * ln(n+1) / ln(n)|
As n approaches infinity, the limit simplifies to:
| x / 2 |
For the series to converge, this limit must be less than 1:
|x / 2| < 1
Solving for x, we have:
-1 < x/2 < 1
Multiplying by 2, we get:
-2 < x < 2
Therefore, the radius of convergence, r, is 2. The series converges for values of x within the interval (-2, 2).
Learn more about convergence here:
https://brainly.com/question/14394994
#SPJ11
Got this one wrong need help

Answers
so let’s start by solving the equations:
6 + 4 = 10
2(6) - 3 = 9
3(6) - 10 = 8
then order then look at what each of the sides is opposite to:
10 = A
9 = B
8 = C
so from smallest to largest the angles are C, B, A
May 23, 8:49:32 PM
Watch help video
In physics lab, Austin attaches a wireless sensor to one of the spokes of a bicycle
wheel spinning freely on its axle. The sensor's height above the ground, in
centimeters, is given by the function h(t) = 7.46 cos(2(t-0.25)) + 38.86,
where t is time measured in seconds.
What is the minimum and what does it represent in this
context?
Answers
The minimum is 29 cm and it represents the sensor's minimum height above the ground.
How to interpret the graph of a cosine function?In Mathematics and Geometry, the standard form of a cosine function can be represented or modeled by the following mathematical equation (formula):
y = Acos(Bx - C) + D
Where:
A represents the amplitude.B = 2π/P.P represents the period.C represents the phase shift.D represents the center line (midline).By critically observing the graph which models the sensor's height above the ground (in centimeters) shown in the image attached below, we can reasonably infer and logically deduce that it has a minimum height of 29 centimeters.
In conclusion, the sensor's minimum height above the ground cannot exceed 29 centimeters.
Read more on cosine function here: brainly.com/question/26993851
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.
