Homework: Chapter 14 C Find the indicated term of the geometric sequence. 3,6, 12, 24, the 7th term The 7th term of the geometric sequence is гу Help me solve this View an example Textbook
Answers
The 7th term of the geometric sequence 3, 6, 12, 24, ... is 5184. A geometric sequence is a sequence of numbers where each term is multiplied by a constant value to get the next term.
In this case, the constant value is 2. To find the 7th term, we can use the formula:
a_n = a_1 r^(n-1)
where a_n is the nth term, a_1 is the first term, and r is the common ratio.
Plugging in the values, we get:
a_7 = 3 * 2^(7-1) = 3 * 2^6 = 3 * 64 = 5184
In words, we can solve this problem by first finding the common ratio of the geometric sequence. This is done by dividing any two consecutive terms. In this case, the common ratio is 2. Once we know the common ratio, we can use the formula above to find the 7th term. Additional Information:
The geometric sequence is a powerful tool that can be used to model a variety of real-world phenomena. For example, it can be used to model the growth of a population, the decline of a radioactive substance, or the interest earned on a savings account.
Learn more about radioactive substances here:- brainly.com/question/32673718
#SPJ11
Related Questions
Can someone help me I need it to be broken down

Answers
Answer:
\(x + 23 + x + 80 = 180 \\ 2x + 103 = 180 \\ 2x = 77 \\ x = 38.5\)
Remember that Molly has a $2500 down payment saved for this purchase. The dealer will take the $500 Cash Allowance straight off her total. How much loan does Molly need?
Using the Loan Calculator and the 1.9% APR offer, how much will Molly’s monthly payment be?
How much total interest will Molly pay using this plan?
When Molly adds all of her payments, how much will the car cost her using this plan?
Answers
To determine the loan amount Molly needs, subtract the down payment and cash allowance from the total cost of the car.
Loan amount = Total cost - Down payment - Cash allowance
To calculate Molly's monthly payment, use the Loan Calculator with the loan amount, loan term in months, and the APR of 1.9%.
To find the total interest paid, subtract the loan amount from the product of the monthly payment and the loan term.
To calculate the total cost of the car, add the down payment, cash allowance, loan amount, and total interest paid.
To calculate the loan amount Molly needs, we subtract the down payment and cash allowance from the total cost of the car. Let's assume the total cost is $X.
Loan amount = Total cost - Down payment - Cash allowance = X - $2500 - $500 = X - $3000.
To calculate Molly's monthly payment using the Loan Calculator and the 1.9% APR offer, we need to know the loan amount, the loan term in months, and the APR. Let's assume the loan term is Y months.
Using the Loan Calculator, we can determine the monthly payment based on the loan amount, loan term, and APR.
To calculate the total interest Molly will pay using this plan, we can multiply the monthly payment by the loan term in months and subtract the loan amount. This will give us the total interest paid.
Total interest = (Monthly payment * Loan term) - Loan amount.
To calculate the total cost of the car for Molly using this plan, we add the down payment, cash allowance, and the total interest paid to the loan amount.
Total cost = Loan amount + Down payment + Cash allowance + Total interest.
Please provide the values of X and Y to calculate the specific amounts.
Learn more about down payment:
https://brainly.com/question/1698287
#SPJ11
You have the following question on a survey. "What clubs are you involved in". Youselect every 25th student in all the classes to fill out the survey. Classify this survey Is this a random or non random

Answers
Answer: Random
To answer this question, let us first define what Random Sampling is.
Random Sampling describes when every elemnt in a population has an equal chance of being chosen for the sample.
There are 4 types of Random Sampling, but we are going to focus on one type which is the Systematic Random Sampling.
Systematic Random Sampling is a common technique where sample every kth element. For example, surveying every 100th person that walks in a mall.
Now based on the question, it is stated that "You select every 25th student in all the classes". This is an example of Systematic Random Sampling.
Therefore this survey is classified as Random.
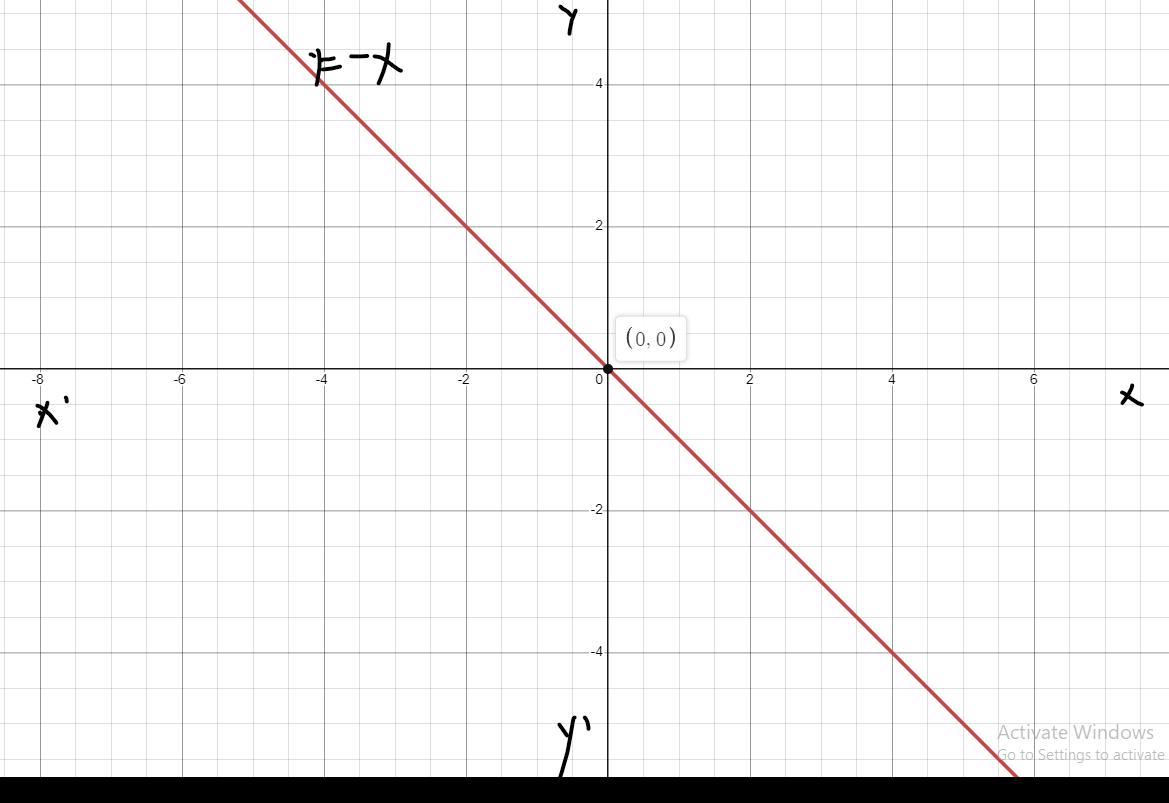
graph the linear function identify the x-intercept.
y=-x
Answers
The x-intercept of the given linear function is 0 and the graph of the linear ufnction is shown.
What is the x-intercept?A line's x-intercept and y-intercept are the points at which the x- and y-axes, respectively, are crossed.We set y = 0 and solve the equation for x to determine the x-intercept. This is due to the fact that the line crosses the x-axis at y=0. If an equation is not in the form y = MX + b, we can still solve for the intercepts by substituting 0 where necessary and then solving for the final variable.So, plot the linear function:
Plot y = -x as follows:(Refer to the graph attached below)
We can clearly see that the x-intercept is 0.Therefore, the x-intercept of the given linear function is 0 and the graph of the linear ufnction is shown.
Know more about the x-intercept here:
https://brainly.com/question/17932786
#SPJ1
Suppose a triangle has angle measures of 29 degrees and 52 degrees. What is the measure of the third angle?
Answers
Answer:
99 degrees
Step-by-step explanation:
all triangles equal 180 degrees total. add up the 2 angles you know (29+52) then subtract it from 180. 180-81=99
What type of function is f(x) = 7 * (5/4) ^ x
Answers
Answer:
exponential growth
Step-by-step explanation:
20-9x+4y+7-x
Need help
Answers
Answer:
\(-10x + 4 y + 27\)
Step-by-step explanation:
Answer: -10x+4y+27
Step-by-step explanation: first, combine the like terms
20 + 7= 27
-9x-x=-10x
4y stays the same so, if simplified this equals
-10x+2y+27
pre-calc questions (trignometry)


Answers
Answer: (1a) 250° (1b) 70° (2) see below
Step-by-step explanation:
1a) -110 + 360 (one rotation clockwise) = 250°
1b) 430 - 360 (one rotation counterclockwise) = 70°
2) sec Ф = -8/5 in Quadrant III
Quadrant III identifies that both sin (y) and cos (x) are negative.
sec = r/x --> r = 8, x = -5, and y = -√39
(Use Pythagorean Theorem x² + y² = r² to solve for y)
\(\sin\theta=\dfrac{y}{r}=\dfrac{-\sqrt{39}}{8}\) \(\csc\theta=\dfrac{r}{y}=\dfrac{-8}{\sqrt{39}}\) rationalized = \(\dfrac{-8\sqrt{39}}{39}\)
\(\cos\theta=\dfrac{x}{r}=\dfrac{-5}{8}\) \(\sec\theta=\dfrac{r}{x}=\dfrac{-8}{5}\) (GIVEN)
\(\tan\theta=\dfrac{y}{x}=\dfrac{\sqrt{39}}{5}\) \(\cot\theta=\dfrac{x}{y}=\dfrac{-5}{-\sqrt{39}}\) rationalized = \(=\dfrac{5\sqrt{39}}{39}\)
NOTE THAT YOU ARE ALLOWED A MAXIMUM OF 3 QUESTIONS PER POST. Please repost #3 and #4 as a different question and I will answer them.
Janine babysits for $14.50 per hour. She also works as a dishwasher at her family's restaurant for $9.50 per hour. Her family needs her to be at the restaurant at least 7 hours per week, but she can't work there more than 10 hours per week. She also does not want to work more than a total of 15 hours each week. She wants to make at least $140 per week.
Write a system of inequalities that represents the constraints on Janine's part-time jobs. Explain what your inequalities represent in the context of the problem.
Janine wants to earn as much money as possible next week. What combination of hours should she spend at each job to do this? Justify your reasoning.
Answers
Answer:
1) The system of inequalities are
14.5·x + 9.5·y ≥ 140
7 ≤ y ≤ 10
x + y ≤ 15
2) 14.5·x + 9.5·y ≥ 140 represents the total amount of money Janine can earn
7 ≤ y ≤ 10 represents the range of values, Janine can spend dishwashing
x + y ≤ 15 represents the total number of hours Janine will like to work each week
3) 8 hours babysitting, 7 hours dishwashing
Step-by-step explanation:
The given parameters are;
The amount per hour Janine makes from babysits = $14.50
The amount per hour Janine makes from dishwashing = $9.50
The minimum number of hours Janine can spend dishwashing = 7 hours
The maximum number of hours Janine can spend dishwashing = 10 hours
The maximum number of hours Janine can work each week = 7 hours
The minimum amount she wants to make each week = $140
Let x represent the number of hours Janine spends babysitting and let y represent the number of hours Janine spends dishwashing
1) From the question, we have;
14.5·x + 9.5·y ≥ 140
7 ≤ y ≤ 10
x + y ≤ 15
2) Where
14.5·x + 9.5·y ≥ 140 represents the total amount of money Janine can earn
7 ≤ y ≤ 10 represents the range of values, Janine can spend dishwashing
x + y ≤ 15 represents the total number of hours Janine will like to work each week
Making, y, the subject of the formula of the above inequalities and plotting as functions is given as follows;
y ≥ 140/9.5 - (14.5/9.5)·x
y ≤ 15 - x
3) In order to earn as much money as possible given that the amount Janine earns from babysitting is more than the amount she earns from dishwashing, Janine should spend the least amount of time dishwashing, which is 7 hours, as given, and then spend the remaining 8 hours babysitting to receive $14.5 × 8 + $9.5×7 = $182.5

Janine should work as a dishwasher for 7 hours, and as a babysitter for 8 hours, to earn as much money
Represent the hours babysitting with b, and the hour dishwashing with d.
So, we have the following systems of inequalities
\(14.5b + 9.5d \ge 140\) ---her earnings\(7\le d \le 10\) -- the time she can spend at the restaurant\(b + d \le 15\) --- her weekly work hoursNext, we plot the graphs of the inequalities that represent the hours she can work.
i.e. the graphs of \(7\le d \le 10\) and \(b + d \le 15\)
From the attached graph, we have the following possible values
\((b,d) =(5,10) (8,7)\)
Substitute these values in \(14.5b + 9.5d \ge 140\)
So, we have:
At (5,10):
\(Earnings = 14.5 \times 5 + 9.5 \times 10\)
\(Earnings = 167.5\)
At (8,7):
\(Earnings = 14.5 \times 8 + 9.5 \times 7\)
\(Earnings = 182.5\)
The earnings at point (8,7) is greater than (5,10).
Hence, she should work as a dishwasher for 7 hours, and as a babysitter for 8 hours, to earn as much money
Read more about inequalities at:
https://brainly.com/question/18881247

The length of a rectangular poster is 10 more inches than three times its width. The area of the poster is 88 square inches. Solve for the dimensions (length and width) of the poster.
The dimensions are ___ inches by___ inches.
Answers
Let's assume that the width of the poster is "x" inches.
According to the problem, the length of the poster is 10 more inches than three times its width. So, the length is (3x + 10) inches.
The area of a rectangle is given by the formula A = length x width. We are given that the area of the poster is 88 square inches. So, we can write:
(3x + 10) x x = 88
Simplifying the above equation, we get:
3x^2 + 10x - 88 = 0
We can solve this quadratic equation by factoring or using the quadratic formula. Let's use the quadratic formula:
x = [-b ± sqrt(b^2 - 4ac)] / 2a
where a = 3, b = 10, and c = -88
Plugging in the values, we get:
x = [-10 ± sqrt(10^2 - 4(3)(-88))] / 2(3)
x = [-10 ± sqrt(1000)] / 6
x = [-10 ± 31.62] / 6
x = 3.27 or x = -8.94
Since the width cannot be negative, we ignore the negative solution. Therefore, the width of the poster is approximately 3.27 inches.
Using this value, we can find the length:
length = 3x + 10 = 3(3.27) + 10 = 19.81 inches (rounded to two decimal places)
Therefore, the dimensions of the poster are approximately 3.27 inches by 19.81 inches.
Answer:
It's just 22
Step-by-step explanation:
22
This scene is an example of dramatic irony used to create suspense since the audience knows that.
Answers
This scene is an example of dramatic irony used to create suspense since the audience knows that this joyous occasion will ultimately lead to tragedy.
In the scene, Lord Capulet is preparing for his daughter Juliet's wedding to Paris, while the audience knows that Juliet is already secretly married to Romeo. Lord Capulet's excitement and eagerness to prepare for the wedding create suspense and tension for the audience, who knows that this joyous occasion will ultimately lead to tragedy.
Furthermore, the use of music within the scene also adds to the suspense. The audience hears the music, which signifies the arrival of the wedding party, but also knows that this will lead to the revelation of Juliet's secret marriage.
The urgency in Lord Capulet's instructions to the Nurse to wake up Juliet and make haste heightens the tension for the audience, who are aware of the impending disaster.
To know more about dramatic irony here
https://brainly.com/question/29797222
#SPJ4
Complete Question:
Read the excerpt from Act IV, scene iii of Romeo and Juliet.
Capulet Good faith! this day:
The county will be here with music straight,
For so he said he would. [Music within.] I hear him near.
35
This scene is an example of dramatic irony used to create suspense since the audience knows that
Practice Solving Distance Problems
Solve.
1. At the beginning of the year, Tonya was 54 inches tall. At the end of
the year she is 561
2 inches tall.
How many inches does Tonya grow during the year?
a. Let i represent the unknown in this problem. What does the
problem ask you to find?
Answers
\(\Huge\green{\tt{✏Answer✏}}\)
The problem asked to find how many inches Tonya grows during the year
\(\Huge\blue{\tt{✏Explanation✏}}\)
here my friend#CarryOnLearning
hit that heart and dont forget to follow hehe thx<3\(\color{blue}{⊱─━━━━━━━━⊱༻●༺⊰━━━━━━━━─⊰}\)
\(\huge{꧁༒Maizen༒꧂}\)
Tell what shape is created by each cross section...

Answers
The shapes from the cross section are square, parallelogram, trapezium, kite, triangle and rectangle.
Shapes formed from the cross sectionIt is important to note that the cross section of a cube is a square.
From the cross section visible from the figure, we have the shapes;
squareParallelogramTrapeziumTriangleKiteRectangleThus, the shapes from the cross section are square, parallelogram, trapezium, kite, triangle and rectangle.
Learn more about cross section of a cube here:
https://brainly.com/question/2156900
#SPJ1
I know the answer is -2 but I need to show my work on how I got it

Answers
Answer:
-2
Step-by-step explanation:
6x + 10 = 1x
Subtract 6x from both sides.
10 = -5x
------------ Divide by -5
-5
-2 = x
6x + 10 = 1x
Subtract 10 from both sides
6x + 10 (-10)= 1x (-10)
6x =1x - 10
Subtract 1x from both sides
6x (-x) = 1x (-x) - 10
5x = -10
Divide both sides by 5
5x (/5) = -10 (/5)
x = -2
Hope that helps :)
find x and I will give you brainliest answer award and 10 points

Answers
Answer: x = 6
Formula: \((x+5)=11\)
Step-by-step explanation:
We know that an area of a triangle is half of a rectangle.
The bottom side must equal 11, since if the figure was a rectangle, the area would be multiplied by 2, giving us 44.
What minus 5 equals 11?
6.
So x must equal 6.
How to find unique prime factorization of 10 factorial.
Answers
add r to q, then add s to the result
Answers
Answer:
(r+q)+s
Step-by-step explanation:
The parentheses make it clear that r and q need to be added first.
an envelope contains eight bills: two $ 1 bills, two $ 5 bills, two $ 10 bills, and two $ 20 bills. two bills are drawn at random without replacement. what is the probability that their sum is $ 20 or more? (a) 1 4 (b) 2 5 (c) 3 7 (d) 1 2 (e) 2 3
Answers
Probability is nothing but the ratio of favorable cases to all possible cases or in simple terms it is the ratio of sample set to all set
We are required to find all the cases in which sum of any two bills is 20$ or more
The total number of bills are two $ 1 bills, two $ 5 bills, two $ 10 bills, and two $ 20 bills.
The total case of drawing any two bills will be =
2 for $ 1 bill x two for 5$ bill x two for 10$ bill x two 20$ bills
=2 x 2x2x2 =16
Hence 16 ways in which two bills can be drawn at random
Cases in which bill can be greater than 20$= (1,20)(20,1)(5,20)(20,5)(10,10)(20,10)(10,20) (20,20)= 8 cases
Hence, total number of possible outcomes = 8
Hence the probability of bill to be 20$ or more= favorable outcome/total outcome
=8/16 =1/2
Hence the probability is 1/2
Disclaimer: the fraction sign is missing in question options
For further reference on probability:
https://brainly.com/question/743546?referrer=searchResults
#SPJ4
What are the quotient and remainder of (2x^4+5x^3-2x-8)/(x+3)

Answers
The quotient of (2x^4 + 5x^3 - 2x - 8) divided by (x + 3) is 2x^3 - x^2 + 3x - 7, and the remainder is 13.
To find the quotient and remainder, we can use polynomial long division.
First, we divide the leading term of the numerator, 2x^4, by the leading term of the denominator, x. This gives us 2x^3.
Next, we multiply the denominator, x + 3, by the quotient term we just found, 2x^3. We subtract this product, which is 2x^4 + 6x^3, from the numerator.
We then repeat the process with the new numerator, which is now -x^3 - 2x - 8.
Dividing the leading term of the new numerator, -x^3, by the leading term of the denominator, x, gives us -x^2.
We continue this process until the degree of the numerator is less than the degree of the denominator.
After finding the quotient, 2x^3 - x^2 + 3x - 7, and the remainder, 13, we can conclude our division.
For more similar questions on remainder
brainly.com/question/18191517
#SPJ8
Landon is going to invest in an account paying an interest rate of 4.3% compounded continuously. How much would Landon need to invest, to the nearest hundred dollars, for the value of the account to reach $11,300 in 14 years?
Answers
Answer:
$ 6,189.18
Step-by-step explanation:
From the above question, we can deduce that we are meant to find the Principal (Initial Amount ) invested.
The formula for the Principal of a compound interest that is compounded continuously is given as:
P = A / e^rt
Where
P = Principal
A = Totally Amount after time t = $11,300
r = Interest rate = 4.3 % = 0.043
t = 14 years
P = $11,300/ e ^0.043 × 14
P = $ 6,189.18
Hence, Landon needs to invest, $ 6,189.18
Answer:
6200
Step-by-step explanation:
Dave is making cookies for his niece. He wants to
make 1/2 batches. If the recipe calls for 2 1/4 cups of
flour for one batch, how much flour will he need to
use for 1 1/2 batches?
Answers
Answer:2.25 + 4.5 = 6.75 cups of flour
2.25
Step-by-step explanation: 1 batch is already 2.25 in decimal form so just infer from there.. divide 2.25 from .5 and get 4.5 then add to the one batch you've already received .. 4.5 + 2.25 = 6.75 and just convert into a fraction 6 3/4
what is limit definition of a derivative?
Answers
The limit definition of a derivative is a mathematical method used to calculate the instant rate of change of a characteristic at a particular point. it is based at the idea of the limit of a function because the input techniques a certain cost.
The limit definition of a derivative is expressed as follows:
\(f'(x) = lim (h → 0) [f(x + h) - f(x)] /h\)
Wherein f'(x) represents the derivative of the function f(x) at a particular factor x. The expression \(( f(x + h) - f(x)) / h\) represents the common price of alternate of the characteristic over a small interval of size h, focused at x. The limit of this expression as h approaches 0 represents the instant fee of change of the characteristic at x, or the slope of the tangent line to the function at that factor.
The limit definition of a derivative is a fundamental concept in calculus and is used to calculate the slopes of tangent lines, to find maximum and minimum factors, and to clear up optimization issues in a huge variety of packages.
Learn more about Limit definition of a derivative:-
https://brainly.com/question/30402318
#SPJ4
You want to buy a new Apple Watch. It costs $279.00, but you have to pay 6% sales tax. How much will the watch cost you with tax?
Answers
Answer:
279.06
Step-by-step explanation:
What is a solution to the system of equations that includes quadratic function f(x) and linear function g(x)?
f(x) = 3x^2 + x + 3

Answers
Answer:
-1 and 4/3
Step-by-step explanation:
So first we want to find the equation for the linear function g(x):
We know that it is linear, so it will follow the equation
y = mx + b
m is the slope, and b is the y-intercept
First, find the slope:
We can see that every time the x increases by 1, the output value is increased by 2
This means that the slope will be 2
Then, find the y-intercept:
The y-intercept is when the x value is equal to 0, so in this table, when the x value is 0, the output is 7
So putting these number into the equation will give us:
y = 2x + 7
Now to find the solutions:
You have to set these equations equal to each other and solve for x
The set up should look like this:
\(3x^{2} + x +3 = 2x+7\)
Put all of the values on one side:
\(3x^{2} -x-4 = 0\)
And then solve for x by factoring:
\(3x^{2} +3x-4x-4\) = 0
\((3x^{2} +3x)+(-4x-4)\) = 0
\(3x(x+1)-4(x+1)\) = 0
(x+1)(3x-4) = 0
Finally, to get the x values:
x + 1 = 0
x = -1
and
3x - 4 = 0
3x = 4
x = 4/3
So the answers are:
x = -1 and 4/3
The solution to the system of equations that includes quadratic function f(x) and linear function g(x) is (-1,5) and (4/3,29/3).
What is a polynomial function?A polynomial function is a relation where a dependent variable is equal to a polynomial expression. A polynomial expression is an expression including numbers and variables, where variables are raised to non-negative powers.
The general form of a polynomial expression is:
a₀ + a₁x + a₂x² + a₃x³ + ... + aₙxⁿ.
The highest power to a variable is the degree of the polynomial expression.
When degree = 2, the function is a quadratic function.
When degree = 1, the function is a linear function.
How do we solve the given question?The quadratic function is given to us:
f(x) = 3x² + x + 3.
We need to determine the linear equation g(x). Since it's a linear equation we use the two-point method to determine the equation.
The two-point formula is:
y-y₁ = ((y₂-y₁)/(x₂-x₁))*(x-x₁)
We take the points g(2) = 11, g(1) = 9
g(x) - g(1) = ((g(2)-g(1))/(2-1))*(x-1)
or, g(x) - 9 = ((11-9)/(2-1))*(x-1)
or, g(x) - 9 = 2(x-1)
or, g(x) = 2x - 2 + 9 = 2x + 7
∴ g(x) = 2x +7, is the linear function g(x)
We are asked to find the solution to the system of equations f(x) and g(x).
To find the solution we need to check what is the common solution to both f(x) and g(x).
For that, we equate f(x) and g(x).
3x² + x + 3 = 2x + 7
or, 3x² - x - 4 = 0
or, 3x² + 3x - 4x - 4 = 0
or, 3x(x+1) -4(x+1) = 0
or, (3x-4)(x+1) = 0
∴ Either 3x-4=0 ⇒ x = 4/3
or, x+1=0 ⇒ x = -1.
g(-1) = 5 (from the table)
f(-1) = 3(-1)² + (-1) + 3 = 3 - 1 + 3 = 5
g(4/3) = 2(4/3) + 7 = 8/3 + 21/3 = 29/3
f(4/3) = 3*(4/3)² + (4/3) + 3 = 16/3 + 4/3 + 9/3 = 29/3
∴ f(-1) = g(-1) and f(4/3) = g(4/3), so
The solution to the system of equations that includes quadratic function f(x) and linear function g(x) is (-1,5) and (4/3,29/3).
Learn more about linear and quadratic equations at
https://brainly.com/question/14075672
#SPJ2
a city recreation department plans to build a rectangular playground having an area of 16,900 square meters and surround it by a fence. how can this be done using the least amount of fence
Answers
On solving the provided question we can say that - Use a 130 m by 90 m fence for the playground's perimeter to use the least amount of fencing possible.
What is Perimeter?A boundary is a closed route that surrounds, encloses, or defines a one-dimensional length or a two-dimensional form. There are various real-world uses for perimeter calculation.
The playground has a 16900m2 space. We discover the factors of 16900 to get the length and width that may be attainable.
factors are - \(26*650, 1300*13, 130*90 and 65*260\)
The formula for a rectangle's perimeter is 2(l+w).
Dimensions 130 and 90 will provide the least amount of perimeter utilising all these criteria.
\(440 i.e 2(130+90)= 440.\)
Therefore, 130m by 90m is the smallest dimension for fencing the playground.
To know more about perimeter visit:
https://brainly.com/question/6465134
#SPJ4
help in don’t know what to do

Answers
Answer:
slope 4
y intercept 0, 4
Step-by-step explanation:
Answer:
Slope: -1
y-intercept: (0, 9)
Step-by-step explanation:
The slope is -1 because -1x is the same as -x and the slope is the number before x. The y-intercept is (0, 9) because the y-intercept is what y is when x is 0 so y = -1(0) + 9 which equals 9.
Consider the system of equations.
5x + 2y = 12
5x – 2y = 28
What is the solution to the system of equations? Show work using substitution or elimination to support your answer.
A (4, -4)
B (-4, 4)
C (5, -6.5)
D (4, 16)
Show how u got the answer.
Answers
Answer:
(4, -4) = (x, y) = A
Step-by-step explanation:
5x + 2y = 12
- (5x - 2y = 28)
4y = -16
y = -4
5x + 2(-4) = 12
5x - 8 = 12
5x = 20
x = 4
write the sentence as an equation 253 is the product of 69 and g
Answers
Answer:
253=69g or 253=69(g)
Step-by-step explanation:
express x in term of y:x/7+2y=6
Answers
Answer:
see explanation
Step-by-step explanation:
Given
\(\frac{x}{7}\) + 2y = 6
Multiply through by 7 to clear the fraction
x + 14y = 42 ( subtract 14y from both sides )
x = 42 - 14y
Find the percentages: 33 1/3 % of 75
Answers
The value of percent for 33 1/3% of 75 is 25.
What is mean by Percentage?A number or ratio that can be expressed as a fraction of 100 or a relative value indicating hundredth part of any quantity is called percentage.
Given that;
The expression is,
⇒ 33 1/3% of 75
Solve for value as;
⇒ 100/3% × 75
⇒ 100/(3×100) × 75
⇒ 75/3
⇒ 25
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ2