Answers
B
C
Those three are the answer
Related Questions
when mixing to colors of paint in equivalent ratios , is the resulting color always the same
Answers
We have the following:
The first thing is to calculate the ratio between both paintings.
After finding the ratios, it can be calculated for any value using a proportionality rule.
\(\frac{2}{10}=\frac{1}{5}\)for example, for 5 cups of blue paint, should be for yellow paint:
\(\begin{gathered} \frac{1}{5}=\frac{5}{x} \\ x=\frac{5\cdot5}{1} \\ x=25 \end{gathered}\)therefore, should be 25 cups of yellow paint
Find the volume of the figure. Round to the nearest tenth if necessary.
1 point
3.4 in
4.8 in
25
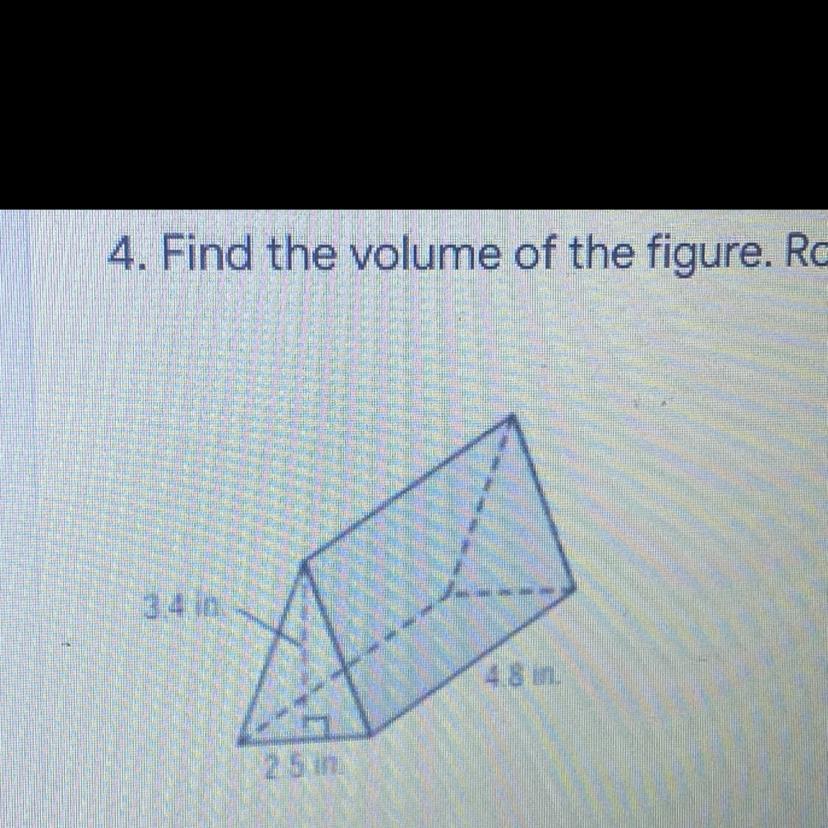
Answers
Answer: 34 in^3
Step-by-step explanation:
Surface area of triangle = 1/2 x 3.4 x 2.5 = 4.25
To find the volume of the prism, multiply the surface area of the triangle by length.
So 4.25 x 8 = 34 in^3
The 40-ft-long A-36 steel rails on a train track are laid with a small gap between them to allow for thermal expansion. The cross-sectional area of each rail is 6.00 in2.
Part B: Using this gap, what would be the axial force in the rails if the temperature were to rise to T3 = 110 ∘F?
Answers
The axial force in the rails if the temperature were to rise to T3 = 110 ∘F is approximately 84 kips.
Given data: Length of A-36 steel rails = 40 ft
Cross-sectional area of each rail = 6.00 in².
The temperature of the steel rails increases from T₁ = 68°F to T₃ = 110°F.Multiply the coefficient of thermal expansion, alpha, by the temperature change and the length of the rail to determine the change in length of the rail:ΔL = alpha * L * ΔT
Where:L is the length of the railΔT is the temperature differencealpha is the coefficient of thermal expansion of A-36 steel. It is given that the coefficient of thermal expansion of A-36 steel is
\(6.5 x 10^−6/°F.ΔL = (6.5 x 10^−6/°F) × 40 ft × (110°F - 68°F)= 0.013 ft = 0.156\)in
This is the change in length of the rail due to the increase in temperature.
There is a small gap between the steel rails to allow for thermal expansion. The change in the length of the rail due to an increase in temperature will be accommodated by the gap. Since there are two rails, the total change in length will be twice this value:
ΔL_total = 2 × ΔL_total = 2 × 0.013 ft = 0.026 ft = 0.312 in
This is the total change in length of both rails due to the increase in temperature.
The axial force in the rails can be calculated using the formula:
F = EA ΔL / L
Given data:
\(E = Young's modulus for A-36 steel = 29 x 10^6 psi = (29 × 10^6) / (12 × 10^3)\)ksiA = cross-sectional area = 6.00 in²ΔL = total change in length of both rails = 0.312 inL = length of both rails = 80 ftF = (EA ΔL) / L= [(29 × 10^6) / (12 × 10^3) ksi] × (6.00 in²) × (0.312 in) / (80 ft)≈ 84 kips
Therefore, the axial force in the rails if the temperature were to rise to T3 = 110 ∘F is approximately 84 kips.
To know more about length visit:
https://brainly.com/question/28322552
#SPJ11
evaluate the integral. 10) ∫ (2x-1) ln(3x) dx
Answers
To evaluate the integral 10) ∫ (2x-1) ln(3x) dx, we will use integration by parts, which involves the formula ∫udv = uv - ∫vdu, where u and dv are differentiable functions.
Step 1: Choose u and dv:
u = ln(3x), so du = (1/x) dx
dv = (2x - 1) dx, so v = x^2 - x
Step 2: Apply integration by parts formula:
∫ (2x-1) ln(3x) dx = uv - ∫vdu
= (x^2 - x)ln(3x) - ∫(x^2 - x)(1/x) dx
Step 3: Simplify the integral:
= (x^2 - x)ln(3x) - ∫(x - 1) dx
Step 4: Integrate the simplified integral:
= (x^2 - x)ln(3x) - (x^2/2 - x). Step 5: Add the constant of integration, C:
= (x^2 - x)ln(3x) - (x^2/2 - x) + C
So, the evaluated integral is ∫ (2x-1) ln(3x) dx = (x^2 - x)ln(3x) - (x^2/2 - x) + C.
Learn more about integrals here, https://brainly.com/question/29813024
#SPJ11
What does 1/6 + 11/12 equal
Answers
someone please help :)

Answers
Answer: 25
Step-by-step explanation:
they are corresponding angles
You are given two metal cubes that look similar. One has an edge of 3. 2 cm long and a mass of 43. 63 g. The other has an edge of 8. 34 cm long and a mass of 683. 5 g. How can you determine if both cubes are made from the same material? select the true statements.
Answers
By solving for the density of the two metal cubes, we can determine that the two metal cubes are not made from the same material.
Density, denoted by ρ, is a property of any substance that is defined as the ratio between the mass and volume of the substance.
ρ = m/v
where ρ = density
m = mass
v = volume
Solving the density of each cube.
Cube 1 :
ρ = m/v
ρ = m/e^3
ρ = 43. 63 g/(3. 2 cm)^3
ρ = 1.3315 g/cm^3
Cube 2 :
ρ = m/v
ρ = m/e^3
ρ = 683. 5 g/(8. 34 cm)^3
ρ = 1.1783 g/cm^3
If two objects have the same density, then they are made from the same material. Since the density of the two cubes are not equal, then they are not made form the same material.
Learn more about density here: https://brainly.com/question/6838128
#SPJ4
Tamar's house is greater than 472 and less than 500 which number can be on Tamar's house?

Answers
490
472 <490<500
it fits the criteria
1.Let x, y be any two numbers that satisfies the conditions x ≠0, y ≠0, and x 0
C.y/x>1
D.x/y<1
2.A pickup truck that can hold up to 3000 pounds is carrying a big machine that is 300 pounds and a few smaller ones that each weigh 60 pounds.
At least how many small machines can you fit so that it will not exceed the weight limit of the truck?
A.no more than 50
B.no less than 50
C.no less than 45
D.no more than 45
3.It usually takes Claude 40 minutes driving at 48 miles per hour to go from home to work. But due to road maintenance today, Claude has to take a detour, which makes the trip 8 miles longer than usual. What is the minimum speed Claude should travel so that he can reach the destination in less than 48 minutes?
A.30 miles per hour
B.56 miles per hour
C.50 miles per hour
D.64 miles per hour
*please make sure you answer all the questions please and thank you.
Answers
Answer:
x and y can be any two numbers greater than zero such that y is also greater than x
D.no more than 45
C.50 miles per hour
Step-by-step explanation:
Let the two numbers be such that x< y because we have been given y/x>1 and x/y< 1 .
Suppose we take y= 9 and x= 3 then
9/3 > 1
3>1
Also
3/9 < 1
1/3 < 1
x and y can be any two numbers greater than zero such that y is also greater than x
2. Total weight that can be carried is 3000 pounds.
The big machine is 300 pounds. The weight that the truck can carry beside the big machine is 3000-300= 2700 pounds.
The smaller machines weigh 60 pounds
The number of smaller machines that can be carried is 2700 ÷ 60= 45 other than the big machine.
3. Total distance = Speed * time
= 48 * (40/60) = 32 miles
New distance = 32+ 8= 40 miles
New time = 48 minutes
Speed = distance / time = 40/ 48/60= 50 miles per hour
Solve the equation 2(3x + 7) = -22.
O A.
x = 6
B.
x = -6
OC.
x=2
OD.
X = -2
Answers
Answer:
x=−6
Step-by-step explanation:
Answer:
C. x = -6
Step-by-step explanation:
\(2(3x + 7) = -22.\\Step -1: Multiply-through-by-two\\6x + 14= -22\\Collect -like-terms.\\6x= -22-14\\6x =-36\\Divide-both-sides-of-the-equation-by 6\\ = x= -6\)
If f(x)=3x-1 and g(x)= x+2 find (f-g)(x)
Answers
Answer:
\(\boxed{2x-3}\)
Step-by-step explanation:
\(f(x)=3x-1\\ g(x)= x+2\)
\((f-g)(x)\\f(x)-g(x)\)
\((3x-1)-(x+2)\\ 3x-1-x-2\\2x-3\)
a patient needs of a low-dose pain reliever. the pharmacy sends pills marked . how many should be administered? round to the nearest tenth of a pill.
Answers
The pharmacy should send two pills marked for the patient to take.
To answer this question, we can use the formula below;
Dosage = (Amount of Drug x Patient's Weight) / Time
Since we don't have any information about the patient's weight or the time, we can't calculate the dosage.
However, we can calculate the number of pills required.
So, let's proceed with the calculation.
Each pill contains 2.5 mg of the pain reliever.
We need to administer a low dose, so let's assume the dose required is 5 mg.
To administer this dose, we need to give two pills, i.e., 2 x 2.5 = 5mg.
However, the question asks us to round the answer to the nearest tenth of a pill.
Since we can't divide a pill into parts, we need to round the answer up or down to the nearest whole pill.
In this case, since we need two pills, the answer is 2 pills.
For similar question on administer.
https://brainly.com/question/13152057
#SPJ11
Please answer correctly !!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!!!

Answers
Answer:
The distance is 7 units between point D and point E

help please! thank u

Answers
b is a function because for each x you get ONLY one y
A parabola can be drawn given a focus of
(-8, 1) and a directrix of y=-1. What
can be said about the parabola?
The parabola has a vertex at
( , ) has a p-value of ( )
and it
Answers
We can say about the parabola given a focus of (-8, 1) and a directrix of y = -1 is as:
The parabola is a vertical parabola and facing up.The vertex of the parabola is v(-8, 0).p value of the parabola is 1.A parabola refers to the shape that traces the equation of the form ax² + bx + c.
A parabola's directrix is a vertical or horizontal line that never contacts the parabola and is located at p distance from the vertex and 2p distance from the focus.
The parabola created when the directrix is on the y coordinate called a vertical parabola.
If the directrix value is greater than the corresponding focus or vertex, there will be a negative p and the parabola will face downhill.
If the directrix value is less than the corresponding focus or vertex, there will be positive p and the parabola will face up.
From the given definition of the directrix, we can find the value of p;
2p = y coordinate of focus - equation of the directrix
2p = 1 - (-1)
2p = 2
p = 1
Vertex, v(h, k) compared with f(h, k + p), we will get;
k + p = 1
k = 0
Therefore, the vertex is (-8, 0).
Thus, we can say about the parabola given a focus of (-8, 1) and a directrix of y = -1 is as:
The parabola is a vertical parabola and facing down.The vertex of the parabola is v(-8, 0).p value of the parabola is 1.To learn more about directrix of a parabola visit:
https://brainly.com/question/29321376
#SPJ1
A student wants to buy 4 bottles of lemonade that cost $1.65 each . if they pay with a bill how much will they get back?
Answers
Answer:
$3.40
Step-by-step explanation:
"A bill" = "1 bill"
Possibile bills = $1, $5, $10, $20, $50, $100
4 × 1.65 = 6.6
$6.60 is more than $5, but less than $10
Since the student is only using a single bill, it must be the $10 bill
10 - 6.6 = 3.4
$3.40
The first Epistle of John was written about A.D is :
45
60-65
90-95
97
Answers
The first Epistle of John was written about AD of between 95 and 110 . So, by this our option should be 97 AD, which is true.
The Fourth of the Catholic Epistles, The First Epistle of John[a] is the first of the Johannine epistles in the New Testament. The authorship of the Johannine writings is disputed among academics. The First Epistle's author is identified as John the Evangelist, who most scholars do not consider to be the same person as John the Apostle. The three Johannine epistles are thought to have been written by the same person by the majority of scholars, however it is unclear if the same person wrote the Gospel of John.
Learn more about Epistle here:
https://brainly.com/question/30006419
#SPJ4
Tickets for a local dog show cost $9.75 each. What is the total cost c, in dollars, for t tickets?
Answers
Answer:
c=1t
Step-by-step explanation:
What is the value of -2|6x - y| when x = -3 and y = 4?
O-44
O-28
O 28
O 44
Answers
Answer:
-44
Step-by-step explanation:
-2|6 * -3 - 4|
-2|-18-4|
-2|-22|
-2 * 22
-44
The mean score on a driving exam for a group of driver’s education students is 84 points, with a standard deviation of 5 points. Apply chebychev’s theorem to the data using k= 12 interpret the results
Answers
Answer:
Step-by-step explanation: There are 8 people in the gym.
An hour later, there are double that number.
How many people are in the gym now?
convert 2 Bigha into kattha
Answers
Answer:
To convert 2 Bigha into Kattha:
If 1 Bigha = 20 Kattha:
2 Bigha = 2 * 20 Kattha = 40 Kattha
If 1 Bigha = 16 Kattha:
2 Bigha = 2 * 16 Kattha = 32 Kattha
Use the Parabola tool to graph the quadratic function.
f(x)=3x^2−6x+5
Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.

Answers
graphed below:
\(\sf f(x)=3x^2-6x+5\)
vertex: (1, 2)cuts y-axis: (0, 5)
Answer:
Given function: \(f(x)=3x^2-6x+5\)
Vertex form: \(y=a(x-h)^2+k\)
(where \((h, k)\) is the vertex)
Expand vertex form:
\(y=ax^2-2ahx+ah^2+k\)
Compare coefficients of given function with expanded vertex form
Comparing coefficient of \(x^2\):
\(3=a\)
Comparing coefficient of \(x\):
\(\ \ \ \ \ -6=-2ah\\\implies-6=-2 \cdot 3h\\\implies -6=-6h\\\implies h=1\)
Comparing constant:
\(\ \ \ \ \ \ 5=ah^2+k\\\implies5=3(1)^2+k \\\implies 5=3+k\\\implies k=2\)
Therefore, the vertex is (1, 2)
As the leading coefficient is positive, the parabola will open upwards.
Additional plot points:
\(f(0)=3(0)^2-6(0)+5=5\)
\(f(2)=3(2)^2-6(2)+5=5\)
(0, 5) and (2, 5)

Please help me, i’m stuck in this answer

Answers
Answer:
I think it stays the same.
Step-by-step explanation:
Solve
h-w
Solve m = for the
8
variable h.
I
Answers
Answer:
1) m = h - w/8
Subtract h from both sides.
m - h = -w/8
Subtract m from both sides.
-h = -m - w/8
Divide all terms by -1.
h = m + w/8.
2) m = h - w/8
Get rid of the denominator 8 by multiplying 8/1 to all terms.
8m = 8h - w
Add w on both sides and subtract 8m from both sides.
w = 8h - 8m
3) w = x + y/z
Get rid of the denominator z by multiplying it to all terms.
wz = xz + y
Subtract xz from both sides of the equation.
wz - xz = y OR y = wz - xz
4) w = x + y/z
Subtract x from both sides.
w - x = y/z
Get rid of the denominator by multiplying it to all terms.
wz - xz = y
Now factor the expression wz - xz.
z(w - x) = y
Divide both sides by w - x.
z = y / w - x
This is read as z equals to y divided by w minus x.
5) The area of a triangle is A = 1/2bh
First, get rid of the denominator by multiplying both sides by 2.
2A = bh
To find b, divide both sides by h.
2A/h = b
6) P = kt/v
Multiply both sides by v.
Pv = kt
Divide both sides by t.
Pv/t = k OR k = Pv/t.
Step-by-step explanation:
exponent rules: (6m⁸n⁹) (4mn⁷) = ?
please help
Answers
The value of the given equation is, (6m⁸n⁹) (4mn⁷) =\($$=24 m^9 n^{16}$$\)
What is exponent rules?(am)n = am*n is the exponent power rule. Exponent times power is how you raise a number with an exponent to a power. The x-n = 1/xn Negative Exponent Rule. A negative exponent can become positive by inverting the base. According to the first law, adding the exponents will multiply two exponential functions with the same base. According to the second law, we must subtract the exponents when dividing two exponential functions with the same base. The third law indicates that we must multiply the exponents in order to increase a power to a new power.Simplify\($\left(6 m^8 n^9\right)\left(4 m n^7\right): \quad 24 m^9 n^{16}$\)
steps
\($$\left(6 m^8 n^9\right)\left(4 m n^7\right)$$\)
Apply exponent rule: \($a^b \cdot a^c=a^{b+c}=0^{\prime}=$\)
\(& m^8 m=m^{8+1} \\\)
\(& =6 n^9 \cdot 4 m^{8+1} n^7\)
\end{aligned}
Add the numbers: \($8+1=9$\)
\(=6 n^9 \cdot 4 m^9 n^7\)
Apply exponent rule: \($a^b \cdot a^c=a^{b+c}$\)
\(& n^9 n^7=n^{9+7} \\\)
\(& =6 \cdot 4 m^9 n^{9+7}\)
Add the numbers: \($9+7=16$\)
\($$=6 \cdot 4 m^9 n^{16}$$\)
Multiply the numbers: 6 - \($4=24$\)
\($$=24 m^9 n^{16}$$\)
To learn more about exponent rules refer o:
https://brainly.com/question/11975096
#SPJ1
Find the value of (525)² - (475² using sutible identite
Answers
Answer:
Step-by-step explanation:
a² - b² = (a +b)(a - b)
a = 525 & b = 475
525² - 475² = (525 + 475) (525 - 475)
=1000 * 50
= 50,000
The value of (525)² - (475)² using the identity (a²- b²) = (a+b) (a-b) is 50000.
The expression given is:
(525)² - (475)²
The above expression looks similar to the expression (a²- b²).
What is the simplified form of expression (a²- b²)?The simplified form of the expression (a²- b²) is (a+b) (a-b).
So, (525)² - (475)² can be written as:
(525)² - (475)² = (525+475) (525-475)
(525)² - (475)² = 1000 * 50
(525)² - (475)² = 50000
Therefore, the value of (525)² - (475)² using the identity (a²- b²) = (a+b) (a-b) is 50000.
To get more about algebraic identities visit:
https://brainly.com/question/1528309
The super sub at Sandwich Station consists of 4 different toppings and 3 different condiments. How many different super subs can be made if there are 8 toppings, 6 condiments, and 6 types of homemade bread to choose from?
Answers
Therefore, there are 53,248 different super subs that can be made if there are 8 toppings, 6 condiments, and 6 types of homemade bread to choose from at Sandwich Station.
The super sub at Sandwich Station consists of 4 different toppings and 3 different condiments. The question is asking how many different super subs can be made if there are 8 toppings, 6 condiments, and 6 types of homemade bread to choose from.
To solve this problem, we can use the multiplication principle of counting. The multiplication principle states that if there are m ways to do one thing and n ways to do another thing, then there are m x n ways to do both things.
Let's use the multiplication principle to solve this problem. There are four different toppings, and we can choose any of the eight toppings for each of the four spots.
Using the multiplication principle, there are
8 x 8 x 8 x 8 = 4096
ways to choose the toppings. Similarly, there are
6 x 6 x 6 = 216
ways to choose the condiments. Lastly, there are 6 different types of homemade bread to choose from. Using the multiplication principle again, there are
4096 x 216 x 6 = 53,248,
which means there are 53,248 ways to make the super subs.
For such more question on multiplication
https://brainly.com/question/29793687
#SPJ8
150 decreased by 15 percent
Answers
Answer:127.5
Step-by-step explanation:
15% of 150 = 22.5
150-22.5=127.5
Answer:
Step-by-step explanation:
look at the image for the question and answers

Answers
Answer:
C
Step-by-step explanation:
Answer:
2 units
Step-by-step explanation:
Using the given formula
P = 2(l + w)
= 2(\(\frac{2}{3}\) + \(\frac{1}{3}\) )
= 2(1)
= 2 units
According to exponent rules, when we multiply terms with the same base we _______ the exponents.
a. Divide
b. Multiply
c. Subtract
d. Add
Answers
According to exponent rules, when we multiply terms with the same base add the exponents. Hence, the correct answer is option D.
Exponent rules are a set of rules that dictate how exponents (numbers written as a superscript) can be manipulated in mathematical operations. Some of the most commonly used exponent rules include:
Product of Powers: When multiplying powers with the same base, you can add the exponents.For example, \(x^4 * x^5 = x^{4+5} = x^9\)
The quotient of Powers: When dividing powers with the same base, you can subtract the exponents.For example, \(x^7 / x^3 = x^{7-3} = x^4\)
Power of a Power: When raising a power to another power, you can multiply the exponents.For example,\((x^3)^5 = x^{3*5} = x^{15}\)
Power of a Product: When raising a product to power, you can raise each factor to that power.For example,\((xy)^3 = x^3 * y^3\)
Power of a Quotient: When raising a quotient to a power, you can raise the numerator and denominator to that power separately.For example,\((x/y)^3 = x^3 / y^3\)
According to the product of the power rule, we get that we add the exponents when we multiply terms with the same base.
Read more about Exponents:
brainly.com/question/25263760
#SPJ4
