Answers
Related Questions
hii please help i’ll give brainliest if you give a correct answer!

Answers
Answer:
8
Step-by-step explanation:
Two sides of a triangle measure 17 inches and 9 inches. Which cannot be the length of the remaining side?
Answers
Answer: B. 26
Step-by-step explanation:
The options are:
A. 21
B. 26
C. 9
D. 15
Let the third side of the triangle be x.
Since the two sides of a triangle measure 17 inches and 9 inches, therefore we can form a triangle inequality with the figures given. This would be:
x + 9 > 17
x > 17 - 9
x > 8
Also,
x < 9 + 17
x < 26
Therefore, 8 < x < 26
Therefore, the answer is 26.
Answer:
see below
Step-by-step explanation:

Choose the diagram that shows the graph of the inequality.

Answers
A random sample of eleven packages was selected from a machine packaging salt in packages marked 500g. The actual weights of salt in kg were: 498 502 505 503 495 499 501 502 505 499 503 Assuming that the weights are normally distributed, calculate a 95% confidence interval for the mean weight of salt in packages marked 500g.
Answers
The 95% confidence interval for the mean weight of salt in packages marked 500g is (498.59g, 503.41g).
To calculate the confidence interval, we can use the formula:
Confidence Interval = sample mean ± (critical value * standard deviation / sqrt(sample size))
First, we need to calculate the sample mean, which is the average of the weights:
Sample Mean = (498 + 502 + 505 + 503 + 495 + 499 + 501 + 502 + 505 + 499 + 503) / 11 = 501.36g
Next, we need to calculate the standard deviation of the sample. We can use the formula for the sample standard deviation:
Sample Standard Deviation = sqrt((sum of (weight - sample mean)^2) / (sample size - 1))
Plugging in the values, we get:
Sample Standard Deviation = sqrt(((498-501.36)^2 + (502-501.36)^2 + ... + (503-501.36)^2) / (11-1)) = 3.21g
The critical value for a 95% confidence interval can be obtained from the t-distribution table or using statistical software. For a sample size of 11 and a confidence level of 95%, the critical value is approximately 2.228.
Finally, we can calculate the confidence interval:
Confidence Interval = 501.36g ± (2.228 * 3.21g / sqrt(11)) ≈ (498.59g, 503.41g)
This means that we are 95% confident that the true mean weight of salt in packages marked 500g lies between 498.59g and 503.41g.
Learn more about mean here:
brainly.com/question/31101410
#SPJ11
Given the exponential decay function f (t) = 2(0. 95) find the average
rate of change from x =0 to x =4. Show your work.
Answers
The average rate of change is -0.1295, under the condition the given exponential decay function is f (t) = 2(0. 95).
In order to find the average rate of change from x=0 to x=4 for the given exponential decay function \(f(t) = 2(0.95)^{t}\), we need to find the slope of the line that passes through the points (0,f(0)) and (4,f(4)).
f(0) = 2(0.95)⁰ = 2
f(4) = 2(0.95)⁴ ≈ 1.482
The slope of the line passing through these two points is:
(f(4) - f(0))/(4 - 0)
= (1.482 - 2)/4
≈ -0.1295
Therefore, the average rate of change from x=0 to x=4 is approximately -0.1295.
An exponential decay function is a form of a function that reduces at a constant rate over time. It is a type of mathematical model used to present many real-world phenomena such as radioactive decay, population growth, and the depreciation of assets.
To learn more about exponential decay function
https://brainly.com/question/27822382
#SPJ4
Given the sequence: -1, 2, 5, 8 what is a(2)?
Answers
Answer:
Your just going to keep adding 3 and the 2 is there because you had negative -1 and then you added 3 so hope this helps probably not what you looking for but hope this helps. Have a good day.
Step-by-step explanation:
Hhhhhhhhhhjhhjhhjhjjjjjjhhhhhhhhhh
Answers
Answer:
i know right? It's so difficult till I'm brainless when I try to solving it
Answer:
same tbh
Step-by-step explanation:
30 points. Need some help with this
Answers
Answer:
I dont see any question
Step-by-step explanation:
Answer:
where is the question????
HELLOPPPPPPPP ASAPPPPPP PLEASEEEE

Answers
Answer:
A.
Step-by-step explanation:
HELP!!!!!!!! ASAP!!!!!!!
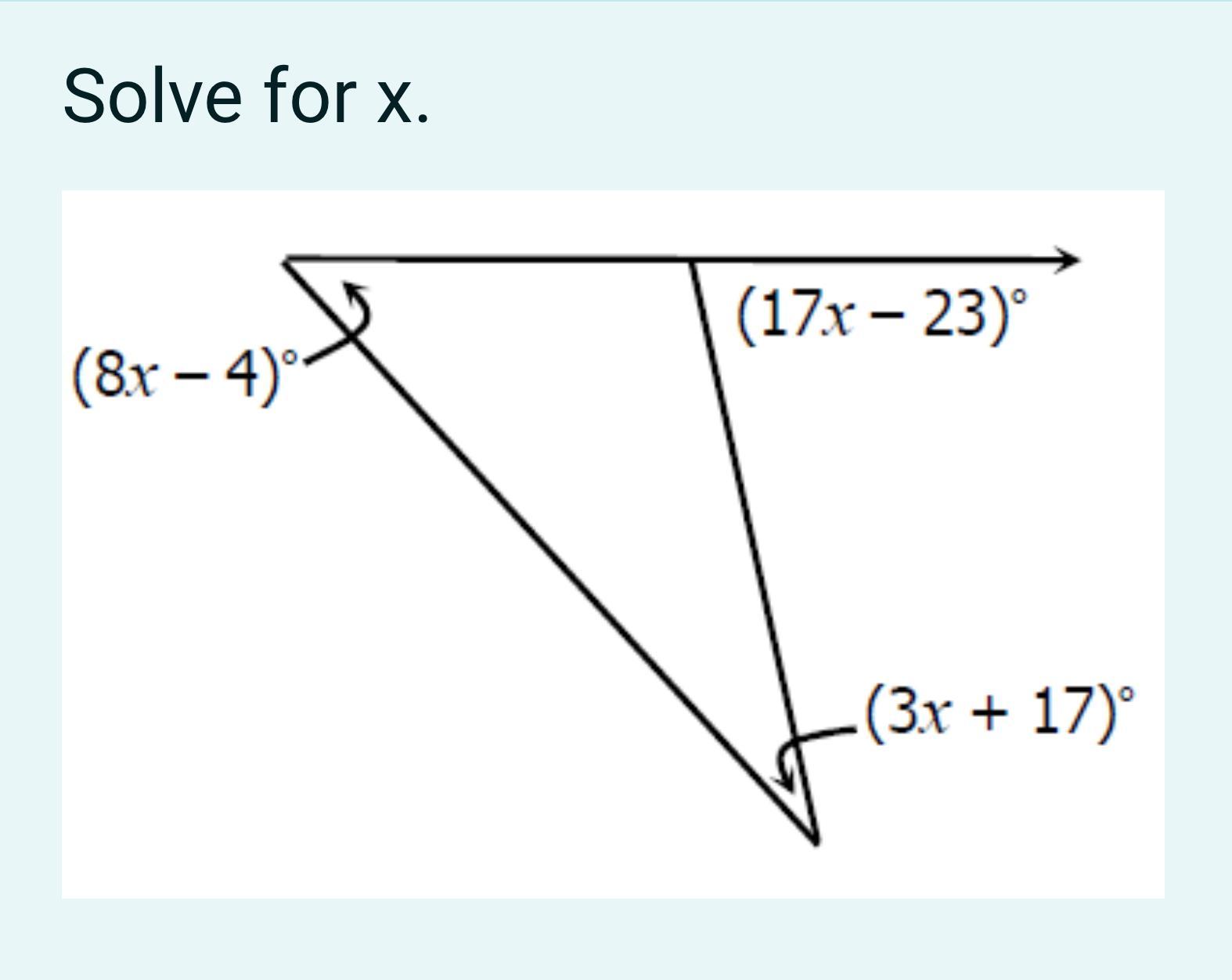
Answers
Using the exterior angle theorem of a triangle, the value of x is 6
Calculating the value of x in a triangleFrom the question, we are to determine the value of x in the given triangle
From one of triangle theorems, we have that
"In a triangle, the exterior angle is always equal to the sum of the interior opposite angle"
In the given diagram,
The exterior angle is (17x - 23)°
and
The two interior angles are (8x -4)° and (3x + 17)°
Thus,
From the theorem, we can write that
(17x - 23)° = (8x -4)° + (3x + 17)°
Now, solve for x
17x - 23 = 8x -4 + 3x + 17
Collect like terms
17x - 8x - 3x = -4 + 17 + 23
6x = 36
x = 36/6
x = 6
Hence, the value of x is 6
Learn more on Calculating the value of x in a triangle here: https://brainly.com/question/29057829
#SPJ1
what is the result of the following boolean expression, if x equals 5, y equals 3, and z equals 8? x < y and z > x
Answers
If x<y and z>x then the solution is true.
What is meant by Boolean operators?Boolean operators are straightforward words (AND, OR, NOT, or AND NOT) that are used as conjunctions in searches to combine or exclude terms, producing more specialized and useful results.
What are Boolean and examples?An expression that may only be evaluated as true or false is called a boolean expression (after mathematician George Boole). Let's examine some examples in everyday language: Pink is one of my favorite colors. I'm apprehensive about programming computers.
From the above theory we can say that
if x=5, y=3 and z=8
and if the conditions are x<y or z>x
Then it is true
as one of them is correct.
To know more about boolean expression click the following link
https://brainly.com/question/25039269
#SPJ1
if 2100 square centimeters of material is available to make a box with a square base and an open top, find the largest possible volume of the box.
Answers
The dimensions of the box that maximize the volume are x = √700 and h = 100 / √700.
To find the largest possible volume of the box, we need to optimize the dimensions of the box. Let's denote the length of each side of the square base as x and the height of the box as h.
The surface area of the box consists of the area of the square base (x^2) and the four sides of the box (4xh). Since the box has an open top, we do not consider the top surface. The total surface area is given as 2100 square centimeters, so we have:
x^2 + 4xh = 2100
To maximize the volume, we need to express the volume of the box (V) in terms of a single variable. The volume of a rectangular prism is given by V = x^2h.
We can rewrite the equation for the surface area to solve for h:
h = (2100 - x^2) / (4x)
Now we can substitute this expression for h in the volume equation:
V = x^2 * [(2100 - x^2) / (4x)]
Simplifying, we have:
V = (1/4) * (2100x - x^3)
To find the maximum volume, we need to find the critical points of this function. We take the derivative of V with respect to x and set it equal to zero:
dV/dx = 2100/4 - (3/4)x^2 = 0
Solving this equation, we find:
2100/4 = (3/4)x^2
x^2 = 700
x = √700
Substituting this value back into the equation for h, we find:
h = (2100 - 700) / (4 * √700) = 1400 / (4 * √700) = 100 / √700
Therefore, the largest possible volume of the box is:
V = (1/4) * (2100 * √700 - 700 * √700) = 350√700 cubic centimeters.
Know more about volume here;
https://brainly.com/question/1578538
#SPJ11
Which of these expression is equivalent to 10% . 10%?
A. 100'
B. 103
C. 10,000,000
D. 2010
E. 107
what expression is equivalent to

Answers
100 points to answer this

Answers
tan (0.9269428)
Decimal form=1.33235488...
Answer:
the answer is 2.4 .
Step-by-step explanation:
plug in arccos(5/13) in the calculator and u will get 67.380, then plug that value in for tan and you will get 2.4.
The ratio of the number of cars to dolls in a toy store is 3/20 . The ratio of the number of male dolls to the number of female dolls is 3:5 There are 500 female dolls. How many toys are there?
Answers
Answer:
800 dolls
Step-by-step explanation:
Step one:
given data
we are told that the ratio of the number of male dolls to the number of female dolls is 3:5 , i.e male dolls to female dolls is 3 to 5
given that there are 500 female dolls, let the number of male dolls be x
Step two:
3/5= x/500
cross multiply we have
3*500=5x
1500=5x
divide both sides by 5
x=1500/5
x=300
hence there are 300 male dolls
The total dolls is 300+500= 800 dolls
9. For which equation is the solution 6? (1 point)
Ox+6=10
04x=24
Ox-6=12
04=24
Answers
Answer:
04x=24
Step-by-step explanation:
04x=24
divide both sides by 4 to let x stand alone
04x÷4=24÷4
x=6
The table shows the average fuel mileage of Car 1. The graph
shows the average fuel mileage of Car 2. Based on the data,
which car will go farther on 25 gallons of fuel?
A) Car 1 will go farther.
B) Car 2 will go farther.
C) Both cars will travel the same distance.

Answers
Using the graph and the table given: A) Car 1 will go farther.
How to Analyze a Graph and Table of a Relationship?In the image given, the table represents the relationship between amount of fuel (x) and distance covered (y) for car 1, while the graph shows that for car 2.
Using any point on the table, (10, 370), find the unit rate for car 1:
Unit rate for car 1 = 370/10 = 37 miles per gallon.
Therefore, for 25 gallons, we would have:
37 × 25 = 925 miles
Car 1 will go 925 miles.
Using any point on the graph, (2, 52), find the unit rate for car 2:
Unit rate for car 2 = 52/2 = 26 miles per gallon.
Therefore, for 25 gallons, we would have:
26 × 25 = 650 miles
Car 2 will go 650 miles.
In conclusion, Car 1 will go farther
Learn more about graph and tables on:
https://brainly.com/question/1535327
#SPJ1
.Graded problem 1 (10pt) A CT scan uses a rotating X-ray source mounted on a circular ring to capture three dimensional images of a body (see Figure 43.2 on page 521 of the textbook). One rotation of the X-ray source produces one sliced image of the body. A specific CT scan machine has a circular ring with diameter 80 cm (radius 40 cm), and the mass of the X- ray source mounted on the circular ring is 38 kg. The time it takes to capture one sliced image is 350 milliseconds. Assume that the X-ray source rotates at a constant speed. (a) What is the translational speed of the X-ray source in m/s? (2 pt) (b) What is the angular speed of the X-ray source in rad/s? (2 pt) (c) What is the magnitude of the centripetal force on the X-ray source? (2 pt) (d) How many degrees does the X-ray source turn in 100 milliseconds? (2 pt) (e) What is the frequency of the rotation of the X-ray source? (2 pt)
Answers
(a) The translational speed of the X-ray source is approximately 8.95 m/s. (b) The angular speed of the X-ray source is approximately 17.98 rad/s. (c) The magnitude of the centripetal force on the X-ray source is approximately 13,872 N. (d) The X-ray source turns approximately 0.634 degrees in 100 milliseconds. (e) The frequency of the rotation of the X-ray source is approximately 10 Hz.
(a) The translational speed of the X-ray source can be calculated using the formula v = d/t, where d is the circumference of the circular ring (2πr) and t is the time it takes to capture one sliced image (350 milliseconds). Substituting the values, we get v = (2π * 40 cm) / (0.35 s) ≈ 8.95 m/s.
(b) The angular speed of the X-ray source can be calculated using the formula ω = θ/t, where θ is the angle covered by the X-ray source in one rotation (360 degrees or 2π radians) and t is the time it takes to capture one sliced image (350 milliseconds). Substituting the values, we get ω = (2π) / (0.35 s) ≈ 17.98 rad/s.
(c) The centripetal force on the X-ray source can be calculated using the formula Fc = mω²r, where m is the mass of the X-ray source (38 kg), ω is the angular speed (17.98 rad/s), and r is the radius of the circular ring (40 cm or 0.4 m). Substituting the values, we get Fc = (38 kg) * (17.98 rad/s)² * (0.4 m) ≈ 13,872 N.
(d) The angle covered by the X-ray source in 100 milliseconds can be calculated using the formula θ = ωt, where ω is the angular speed (17.98 rad/s) and t is the given time (100 milliseconds or 0.1 s). Substituting the values, we get θ = (17.98 rad/s) * (0.1 s) ≈ 1.798 radians. To convert to degrees, we multiply by (180/π), so the angle is approximately 0.634 degrees.
(e) The frequency of rotation can be calculated using the formula f = 1/t, where t is the time it takes to capture one sliced image (350 milliseconds or 0.35 s). Substituting the value, we get f = 1 / (0.35 s) ≈ 10 Hz.
Learn more about centripetal force here: brainly.com/question/14021112
#SPJ11
Which of the following is a root of the polynomial shown below?
f(x) = x2 + 2x2 - x-2
O A. 1
OB. 3
O c. O
O D. 2
Answers
Answer:
We conclude that option A is true as x = 1 is the root of the polynomial.
Step-by-step explanation:
Given the polynomial
\(f\left(x\right)\:=\:x^2\:+\:2x^2\:-\:x-2\)
Let us determine the root of the polynomial shown below.
\(\:0=\:x^2\:+\:2x^2\:-\:x-2\)
\(0=3x^2-x-2\)
switch sides
\(3x^2-x-2=0\)
as
\(3x^2-x-2=\left(3x+2\right)\left(x-1\right)\)
so the equation becomes
\(\left(3x+2\right)\left(x-1\right)=0\)
Using the zero factor principle
\(3x+2=0\quad \mathrm{or}\quad \:x-1=0\)
solving
\(3x+2=0\)
\(3x=-2\)
\(\frac{3x}{3}=\frac{-2}{3}\)
\(x=-\frac{2}{3}\)
and
\(x-1=0\)
\(x=1\)
The possible roots of the polynomial will be:
\(x=-\frac{2}{3},\:x=1\)
Therefore, from the mentioned options, we conclude that option A is true as x = 1 is the root of the polynomial.
The perimeter of the quadrilateral is 70inch. Find the Lengths of the sides
Each side has an equation:
X-5
X+2
X^2-3x
2x+1
Answers
The lengths of the sides are 3 inches, 10 inches, 40 inches, and 17 inches.
To find the lengths of the sides of the quadrilateral, we need to set the sum of the equations equal to the perimeter and solve for x. The equation will be:
X-5 + X+2 + X^2-3x + 2x+1 = 70
Simplifying the equation:
X^2 + X - 72 = 0
We can use the quadratic formula to solve for x:
X = (-b ± √(b^2-4ac))/(2a)
Where a = 1, b = 1, and c = -72
X = (-1 ± √(1^2-4(1)(-72)))/(2(1))
X = (-1 ± √(289))/(2)
X = (-1 ± 17)/(2)
X = 8 or X = -9
Since the length of a side cannot be negative, we will use X = 8. Now we can plug X back into the equations to find the lengths of the sides:
X-5 = 8-5 = 3 inches
X+2 = 8+2 = 10 inches
X^2-3x = 8^2-3(8) = 40 inches
2x+1 = 2(8)+1 = 17 inches
More questions on quadrilaterals and their calculation can be obtained here: https://brainly.com/question/26757123
#SPJ11
||x-4|-2|<3
Solve for X
Answers
Answer:
x<11
Step-by-step explanation:
x−4(|−2|)<3
Simplifies to:
x−8<3
Let's solve your inequality step-by-step.
x−8<3
Step 1: Add 8 to both sides.
x−8+8<3+8
x<11
write six different iterated triple integrals for the volume of the tetrahedron cut from the first octant by the plane xyz. evaluate the first integral.
Answers
The iterated triple integrals for the volume of the tetrahedron cut from the first octant by the plane XYZ is 84
The term iterated triple integrals means the result of applying integrals to a function of more than one variable (for example or ) in a way that each of the integrals considers some of the variables as given constants.
Here we have to write six different iterated triple integrals for the volume of the tetrahedron cut from the first octant by the plane XYZ and then we have to evaluate the first integral.
Here in this case we will integrate with respect to y first.
Therefore, the iterated integral that we need to compute is,
∬6xy²dA=∫⁴₂∫₁²6xy²dydx
When we per the first stage integral, then we get,
=> ∫⁴₂ (2xy³)₁²dydx
When we expand it then we get,
=> ∫⁴₂ [16x - 2x] dx
=> ∫⁴₂ 14x dx
Then we further integrate this one, then we get.,
=> ∫⁴₂ 14x dx = [7x²]₂⁴
=> [7(4)² - 7(2)²]
=> 112 - 28
=> 84
To know more about Integration here.
https://brainly.com/question/18125359
#SPJ4
a. Use Green's theorem to compute the area inside the ellipse( x²/13²)+(y²/6²)=1. Use the fact that the area can be written as
∫∫D dxdy = (1/2) ∫∂D (-ydx+xdy). Hint: x(t)=13cos(t).
The area is?
Answers
The area inside the ellipse can be computed using Green's theorem, which relates the area of a region to a line integral over its boundary.
To apply Green's theorem, we need to parameterize the boundary of the ellipse. Using x(t) = 13cos(t), we can express y in terms of t as y(t) = 6sin(t).
Next, we compute the derivatives dx/dt and dy/dt:
dx/dt = -13sin(t)
dy/dt = 6cos(t)
Substituting these values into the line integral formula, we have:
(1/2) ∫∂D (-ydx + xdy) = (1/2) ∫₀²π (-6sin(t)(-13sin(t)) + 13cos(t)(6cos(t))) dt
= (1/2) ∫₀²π (78sin²(t) + 78cos²(t)) dt
= (1/2) ∫₀²π 78(dt)
= 39π
Thus, the area inside the ellipse, computed using Green's theorem, is 39π square units.
Learn more about ellipse here : brainly.com/question/20393030
#SPJ11
please help math is an absolute pain

Answers
Answer: 3/5 cm
Step-by-step explanation:
Let the length of the base be x. Then, using the formula for the area of a triangle,
\(\frac{3}{25}=\frac{1}{2} \cdot \frac{2}{5} x\\\\\frac{3}{25}=\frac{1}{5}x\\\\x=\frac{3}{5}\)
choose the equation that represtents the graph

Answers
The equation that represents the graph is y = -(2/3)x + 6 .
The X- intercept is defined as the point at which the line crosses the x axis.
The Y- intercept is defined as the point at which the line crosses the y axis.
When a and b are the x and y intercept of a line then
the equation of line in intercept form is x/a + y/b = 1 .
Form the graph in the question
we can see that the graph crosses the x axis at 9, so it's x intercept is 9.
and the graph crosses the y axis at 6, so it's y intercept is 6.
So the intercept form of the line will be given by
x/9 + y/6 = 1
taking LCM of 6 and 9 as 18 ,
and solving further we get ,
2x/18 + 3y/18 = 1
(2x + 3y)/18 = 1
2x + 3y = 18
3y = 18 - 2x
Dividing both sides by 3 , we get
y = 18/3 - (2/3)x
y = 6 - (2/3)x
y = -(2/3)x + 6
Therefore , the equation that represents that represents the graph is y = -(2/3)x + 6 .
Learn more about Intercepts here
https://brainly.com/question/14180189
#SPJ1
The graph shows the relationship between the United States dollar and the euro, the currency of the European Union, in December 2011. Part B: Justify why the relationship shown in the graph is a proportional relationship.

Answers
Answer:
Step-by-step explanation:
Let the equation of the line representing relation between the euros and dollars is,
E = mD + b
Where 'E' = Number of euros
D = Number of dollars
m = slope of the line
b = y-intercept
Slope of a line which passes through two points (120, 90) and (400, 300) will be,
m = \(\frac{y_2-y_1}{x_2-x_1}\) = \(\frac{300-90}{400-120}\)
m = 0.75
Equation of the line passing through (120, 90),
90 = 0.75(120) + b
b = 90 - 90 = 0
Therefore, equation of the line will be,
E = mD
E ∝ D
Here m = Proportionality constant
And the relation between the numbers of Euros and US dollars is a proportional relationship.
find the inverse
will mark brainliest

Answers
Answer:
\(f^{-1} (x) = \sqrt[3]{\frac{1 - 9x^{2} }{x^{2} } }\)
Step-by-step explanation:
Let f(x) = y
Interchange x and y so
\(x = \frac{1}{\sqrt{y^{3} + 9 } }\)
\(x\sqrt{y^{3} + 9} = 1\)
\(\sqrt{y^{3} + 9 } = \frac{1}{x}\)
\(y^{3} + 9 = \frac{1}{x^{2} }\)
\(y^{3} = \frac{1}{x^{2} } - 9\) = \(\frac{1 - 9x^{2} }{x^{2} }\)
\(y = \sqrt[3]{\frac{1 - 9x^{2} }{x^{2} } }\)
\(f^{-1} (x) = \sqrt[3]{\frac{1 - 9x^{2} }{x^{2} } }\)
image down below plz and thx answer first and ill give you brailiest

Answers
Simplify the expression to a polynomial in standard form:
(4x - 5)(2x^2 – 3x - 3)

Answers
Answer:
8x³ - 22x² + 3x +15
Step-by-step explanation:
I do quick mathz
Which transformation is this an example of?
A. reflection
B. rotation
C. translation
D. None of these

Answers
Answer:
B. rotation
Step-by-step explanation:
A reflection would mean that the shape would be mirrored across the y-axis or the x-axis. A translation means that nothing about the shape changes except for the location. A dilation (not an answer option but still helpful to know) is the change in size of the shape. And finally, the correct answer for this problem, a rotation means that the shape is rotated at a specific point.
I included a picture that uses a shape to help explain this idea. I hope this helps! Have a lovely day!! :)

explanation: reflection is a mirrored version of it.
translation is where it doesn’t change at all except for where it is.
rotation is where it flips horizontal to vertical over and over.
