Given the polynomial expression 3x^2 + 3bx - 6x - 6b, factor completely.
Answers
Yw! :)
On factoring the polynomial f(x) = \(3x^{2} +3bx-6x-6b\) , we get -
3(x - 2)(x + b).
We have a polynomial expression -
f(x) = \(3x^{2} +3bx-6x-6b\)
We have to factorize this function f(x).
What is a polynomial ?Polynomials are sums of terms of the form k xⁿ, where k is any number and n is a positive integer.
According to question, we have -
f(x) = \(3x^{2} +3bx-6x-6b\)
Now -
\(3x^{2} +3bx-6x-6b\)
Take out 3 common from the expression -
\(3x^{2} +3bx-6x-6b\)
\(3(x^{2} +bx-2x-2b)\)
\(3[(x^{2} +bx) + (-2x-2b)]\\\\3[x(x + b) - 2(x + b)]\\\\3(x-2)(x+b)\)
Hence, on factoring the polynomial f(x) = \(3x^{2} +3bx-6x-6b\) , we get -
3(x - 2)(x + b).
To solve more questions on factorizing polynomials, visit the link below-
https://brainly.com/question/21325059
#SPJ2
Related Questions
Solve for x.
I will give brainliest
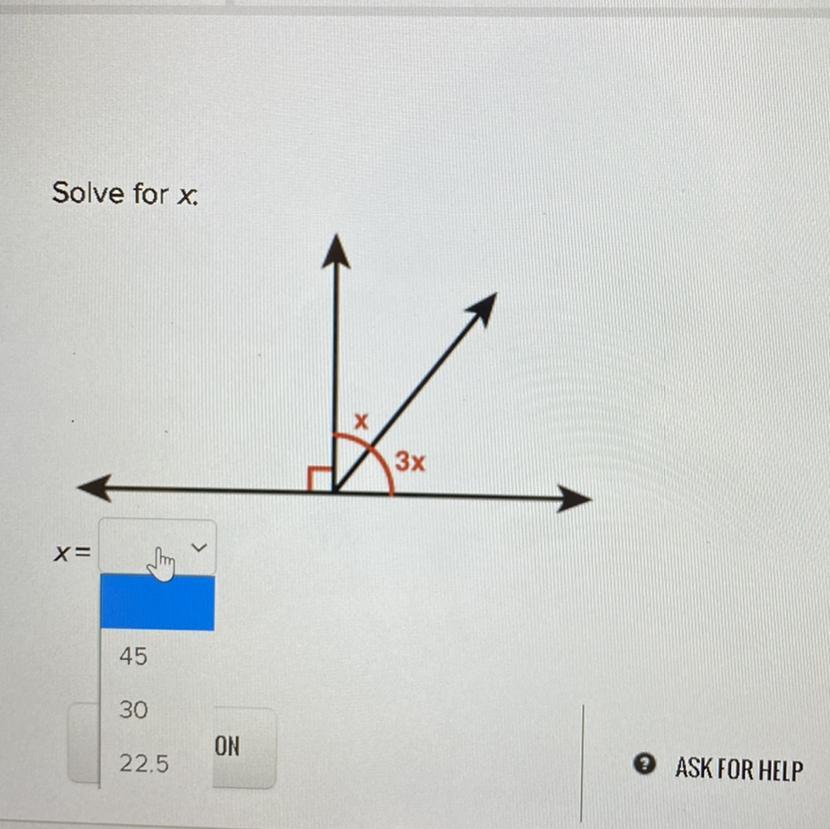
Answers
Answer:
22.5
Step-by-step explanation:
Everything equals 180. This means that the 90 degree angle creates half of that would mean that everything on the right side of the 90 degree angle, also has to equal 90 degrees. X=22.5 because you have to combine like terms meaning x + 3x = 90- 4x=90. Divide by 4 on both sides of the equals sign. Plug that into a calculator and you get 22.5 Since it is only asking for the singular x, you don't have to solve for 3x. (It would be 67.5)
The signed-rank test can be adapted for use in testing H0: μ = hypothesized value, where μ is the mean of a single population (see the last part of this section). Suppose that the time required to process a request at a bank’s automated teller machine is recorded for each of 10 randomly selected transactions, resulting in the following times (in minutes); 1.4, 2.1, 1.9, 1.7, 2.4, 2.9, 1.8, 1.9, 2.6, 2.2. Use the one-sample version of the signed-rank test and a .05 significance level to decide if the data indicate that the mean processing time exceeds 2 minutes.
Answers
Answer:
There is not enough evidence suggesting that the mean processing time exceeds 2 minutes.
Step-by-step explanation:
The hypothesis can be defined as follows:
H₀: The mean processing time is 2 minutes, i.e. μ = 2.
Hₐ: The mean processing time exceeds 2 minutes, i.e. μ > 2.
The significance level of the test is, α = 0.05.
Recorded Time (x) (x - μ) + Ranks -Ranks
1.4 -0.6 8
2.1 0.1 1
1.9 -0.1 1
1.7 -0.3 6
2.4 0.4 7
2.9 0.9 10
1.8 -0.2 4
1.9 -0.1 1
2.6 0.6 8
2.2 0.2 4
TOTAL 30 20
Sum of +Ranks = 30
Sum of -Ranks = 20
Test statistic = Min (∑+Ranks, ∑-Ranks)
= Min (30, 20)
= 20
Compute the critical value using the Wilcoxon Signed-rank test table.
Critical value = 11
As the test statistic value is more than the critical value, the null hypothesis was failed to be rejected.
Thus, there is not enough evidence suggesting that the mean processing time exceeds 2 minutes.

six times the sum of four and a number is 7. what is the number?
Answers
Step-by-step explanation:
6×(4 + x) = 7
24 + 6x = 7
6x = -17
x = -17/6 = -2.833333333... = -2 5/6
We have the number of emergency room admissions to SWTRHA hospital on 6 different Friday the 13ths along with the number of admissions to the same hospital on the previous Friday the 6th. Is there any difference between admissions on the 6th and the 13th. Conduct a depedent samples t-test to find out. What is the value of your t Stat
Answers
Answer:
Test statistic = - 2.71
Step-by-step explanation:
Table of the sample data is attached below :
Using a dependent sample t test :
H0 : μd = 0
H0 : μd ≠ 0
The difference in the 6th and 13th date data is :
Difference, d = -4, -6, -3, -1, 1, -7
The sample size, n = 6
The mean of d ; μd = Σd/ n = - 3.667
Standard deviation of difference, Sd = 3.011
The test statistic : μd/(Sd/√n)
Test statistic = - 3.33 / (3.011/√6)
Test statistic = - 3.33 / 1.2292356
Test statistic = - 2.709
Test statistic = - 2.71

Assume that the halting language \(H_T_M\) is reducible to
some language B (\(H_T_M\) \($\leq$\) \(_m\) B). Is it possible that is decidable? Answer true/false and explain. Please help me this answer?
Answers
H_TM is reduced to HALT_TM and as such, HALT_TM is undecidable.
How to Interpret Machine Language?A language is referred to as Decidable or Recursive if there is a Turing machine that accepts and halts on every input string w. This tells us that every decidable language is Turing-Acceptable.
Now, we are told that the halting language is reducible to some language B. This means that it is an undecidability via reduction.
Now, Using the idea that “ If A is undecidable and reducible to B, then B is undecidable.” Suppose R decides HALT_TM, we will construct S to decide ATM .
S = “On input (M, B)
This means that H_TM is reduced to HALT_TM and as such, HALT_TM is undecidable.
Read more about machine language at; https://brainly.com/question/28026656
#SPJ1
write and equation for the nth term of the geometric sequence for 2,8,32,128
then find a6 round to the nearest tenth if necessary.

Answers
The sixth term of the geometric sequence is 2048.
The given geometric sequence is 2, 8, 32, 128. We can observe that each term is obtained by multiplying the previous term by 4. Therefore, the common ratio (r) of the sequence is 4.
The formula for the nth term (an) of a geometric sequence is given by:
an = a1 * r^(n-1)
where a1 is the first term and r is the common ratio.
For this sequence, a1 = 2 and r = 4. Plugging in these values into the formula, we get:
an = 2 * 4^(n-1)
To find a6, we substitute n = 6 into the formula:
a6 = 2 * 4^(6-1)
= 2 * 4^5
= 2 * 1024
= 2048
For more such questions on geometric,click on
https://brainly.com/question/19241268
#SPJ8
The Probable question may be:
Write an equation for the nth term of the geometric sequence 2, 8, 32, 128,
Then find a6. Round to the nearest tenth if necessary.
a = 5×4 X
a1 = n-1 X
Evaluate
-x^2-4x-4;x=-3
11
-17
3
-1
Answers
Answer:
(-3, -1)
(11, -169)
(-17, -105)
(3, -25)
(-1, -1)
Step-by-step explanation:
-x² - 4x - 4
x = -3
-9 + 12 - 4 = -1
x = 11
-121 - 44 - 4 = - 169
x = -17
-169 + 68 - 4 = -105
x = 3
-9 - 12 - 4 = -25
x = -1
-1 + 4 - 4 = -1
Need help with this question please help !!

Answers
Answer:42
Step-by-step explanation: 84 divide it by 2= 42
hope this helps could i please have brainliest
(3 + 4)2 − 4 × 3 give me a great answer
Answers
Step-by-step explanation:
I'm pretty sure the answer is 2!
Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.
Find the area of the rectangle.
8
2
square units

Answers
16 square units
Musah stands at the centre of a rectangular field. He first takes 50 steps north, then 25 steps
west and finally 50 steps on a bearing of 3150
.
i. Sketch Musah’s movement
ii. How far west is Musah’s final point from the centre?
iii. How far north is Musah’s final point from the centre?
iv. Describe how you would guide a JHS student to find the bearing and distance of
Musah’s final point from the centre.
Answers
Answer:
ii. 75 steps
iii. 75 steps
iv. 106 steps, and \(315^{0}\)
Step-by-step explanation:
Let Musah's starting point be A, his waiting point after taking 50 steps northward and 25 steps westward be B, and his stopping point be C.
ii. From the second attachment, Musah's distance due west from A to C (AD) can be determined as;
bearing at B = \(315^{0}\), therefore <BCD = \(45^{0}\)
To determine distance AB,
\(/AB/^{2}\) = \(/50/^{2}\) + \(/25/^{2}\)
= 25000 + 625
= 3125
AB = \(\sqrt{3125}\)
= 55.90
AB ≅ 56 steps
Thus, AC = 50 steps + 56 steps
= 106 steps
From ΔACD,
Sin \(45^{0}\) = \(\frac{x}{106}\)
⇒ x = 106 × Sin \(45^{0}\)
= 74.9533
≅ 75 steps
Musah's distance west from centre to final point is 75 steps
iii. From the secon attachment, Musah's distance north, y, can be determined by;
Cos \(45^{0}\) = \(\frac{y}{106}\)
⇒ y = 106 × Cos \(45^{0}\)
= 74.9533
≅ 75 steps
Musah's distance north from centre to final point is 75 steps.
iv. Musah's distance from centre to final point is AC = AB + BC
= 50 steps + 56 steps
= 106 steps
From ΔACD,
Tan θ = \(\frac{75}{75}\)
= 1.0
θ = \(Tan^{-1}\) 1.0
= \(45^{0}\)
Musah's bearing from centre to final point = \(45^{0}\) + \(270^{0}\)
= \(315^{0}\)


Determine whether each sequence appears to be an arithmetic
sequence. If so, find the common difference and the next three terms
in the sequence.
1) 3,9,26,81 ...
2) 5,6.5,8,9.5...
Answers
HELP PLEASE M BEGGNG

Answers
Answer:
Min: 1
Q1: 2
Median: 7
Q3: 9
Max: 11.5
Step-by-step explanation:
The five bars of the box plot correspond (from left-to-right) to the numbers in the five-number summary.
The first bar represents the minimum, which in this case is 1.
The second bar represents the first quartile (Q1), which in this case is 2.
The third bar represents the median, which in this case is 7.
The fourth bar represents the third quartile (Q3), which in this case is 9.
And the fifth bar represents the maximum, which in this case is 11.5.
Answer:
Min: 1
Q1: 2
Median: 7
Q3: 9
Max: 11.5
Step-by-step explanation:
I hope it helps:)
Cuál es la circunferencia de un círculo cuyo radio es de 9 cm?
Answers
Porque C= 3.14 • 9^2
Triangles WILL GIVE BRAINLIEST

Answers
Answer:
A
Step-by-step explanation:
A
Answer:
Q9 - Option 1---- A - 15.6 Square Units
Q10 --Option --- (B) RECTANGLE
Step-by-step explanation:
Q9 --
Analyze:we know area of triangle = 1/2 ab sin theta
Where theta is the angle included between sides A and side B
Calculate:A = 5.2
B = 7
theta = 121 degrees
Area:1/2 * 5.2 * 7 * sin 121 degrees = 15.6 Square Units
Conclusion
The area of the triangle is 15.6 Square Units
Q10 - The cross-section of a right cylinder which is perpendicular to its base is a RECTANGLEOption --- (B) RECTANGLE
Hope this helps!
(6x – 30° and m
ZA and ZB are supplementary angles. If mZA
ZB (82 +28)º, then find the measure of ZA.
Answers
9514 1404 393
Answer:
48°
Step-by-step explanation:
Supplementary angles total 180°.
m∠A +m∠B = 180°
(6x -30)° +(8x +28)° = 180°
14x = 182 . . . . . . . . . . . . . . . . divide by ° and add 2
x = 13 . . . . . . . . . . . . . . . . . . . .divide by 14
Then the measure of angle A is ...
m∠A = (6·13 -30)° = 6(13 -5)° = 6·8°
m∠A = 48°
Explain how you can use an array to find partial products for 4x36.
Answers
Answer:
(4 x 30) +(4 x6)
120 + 24
144
Step-by-step explanation:
PLEASEEEE HURRY Which of the following constructions were never accomplished by the Greeks, with only a straight edge and compass
A trisecting any angle
B trisecting a line segment
C tripling a square
D doubling a cube
Answers
Therefore , the solution of the given problem of angles comes out to be Greeks failed to demonstrate that tripling a square with only a straight edge and compass was also unachievable.
An angle meaning is what?The highest and lowest walls of a skew are used to split the curved lines that make up its ends using Cartesian measurements. A collision between two poles at an intersection is a potential. Angle is another outcome of two things interacting. They resemble dihedral forms the most closely. A two-dimensional curve can be created by placing two line beams in various configurations between their ends.
Here,
The Greeks were unable to trisect a line section using only a straight edge and compass.
The Greeks proved that using only a straight edge and compass, it is impossible to trisect any angle or double a cube.
The Greeks failed to demonstrate that tripling a square with only a straight edge and compass was also unachievable.
To know more about angles visit:
https://brainly.com/question/14569348
#SPJ1
ILL GIVE BRAINLESS DUE SOON

Answers
Answer:
Its C
Step-by-step explanation:
On a 28-question test, there are 2-point questions, 4-point questions, and 5-point questions. The test is worth a total of 100 points. There are twice as many 2-point questions as 5-point questions on the test. How many 2-point questions are on the test?
3.Write a series of equations that could be used to solve this. define your varbibles
4.Solveby any algebraic method. Work must be shown.
Answers
Answer:
The test has 8 questions of 2 points, as well as 16 of 4 points and 4 of 5 points.
Step-by-step explanation:
Since, on a 28-question test, there are 2-point questions, 4-point questions, and 5-point questions, the test is worth a total of 100 points and there are twice as many 2-point questions as 5- point questions on the test, to determine how many 2-point questions are on the test, the following calculation must be performed:
18 x 2 + 9 x 5 + 1 x 4 = 36 + 45 + 4 = 85
16 x 2 + 8 x 5 + 4 x 4 = 32 + 40 + 16 = 88
14 x 2 + 7 x 5 + 7 x 4 = 28 + 35 + 28 = 91
12 x 2 + 6 x 5 + 10 x 4 = 24 + 30 + 40 = 94
10 x 2 + 5 x 5 + 13 x 4 = 20 + 25 + 52 = 97
8 x 2 + 4 x 5 + 16 x 4 = 16 + 20 + 64 = 100
Thus, the test has 8 questions of 2 points, as well as 16 of 4 points and 4 of 5 points.
how many jewelry boxes 10 cm by 6 cm by 4 cm can be packed into a box 50 dm long 4 dm wide and 3 dm high? solution pls
Answers
10 × 6 × 4
= 60 × 4
= 240 cm³
50 × 4 × 3
= 200 × 3
= 600 cm³
= 600.000 dm³
600.000 ÷ 240
= 2.500
1.What is the equation of a circle with center (-2, 2) and radius 3?
Answers
Answer:
(x + 2)² + (y - 2)² = 3²
Step-by-step explanation:
Equation of a circle is (x - a)² + (y - b)² = r²,
where a is the x-coordinate of the centre of the circle, b is the y-coordinate of the centre of the circle, r is the circle's radius.
So, we have (x - -2)² + (y - 2)² = 3²
subtract a minus means we add.
(x + 2)² + (y - 2)² = 3²
Is (-3, 1) a solution to this system of inequalities?
5x + 5y ≤ -19
10x 16y < 1
yes or no
Answers
Answer:
No
Step-by-step explanation:
5(-3)= -15
5(1)= 5
-15+5=-10
-10 is greater than -19 not less than or equal too.
Hope this helps!
Help
See the picture

Answers
Answer:
114°
Step-by-step explanation:
The measure of the central angle is going to be the same as the arc, so the answer to this is 114°.
explanation: because the person above me said it lollll
A ski set is on sale for 10% off and for today only customers get an
additional 30% off. This made the final one day sale price of $328. What
was the original seling price of the ski set? *
Answers
Answer:
1034
Step-by-step explanation:
A. Find the Mode, Median, Mean and Range. Show your work.
1. 24, 31, 12, 38, 13, 15, 46, 62.
2. 17, 66, 14, 79, 47, 95, 32, 21, 10, 58.
3. 53, 22, 76, 46, 68, 32, 15, 29.
4. 17, 24, 8, 19, 6, 34, 10, 28, 12.
5. 5, 8, 9, 10, 11, 15, 21, 32.
6. 28, 15, 15, 46, 27, 21, 24
B. Find the mode, median, and range
7) 5.2, 5.7, 5.2, 4.3, 3.6, 3.8, 2.7, 4.2, 4.3, 3.9, 4.2
8) 18.1 , 18.6, 18.2, 18.1, 18.9, 18.6, 18.7, 18.3, 18.2, 18.6, 18.6
C. Find the mode and median for each data.
9) 2/9 , 7/9, 5/9, 1/9, 3/9, 8/9
10) 1/4, 1/11, 1/6, 1/9, 1/3 , 1/10
Answers
A.
1. Mode: No mode. Median: 24. Mean: 30.875. Range: 50.
2. Mode: No mode. Median: 33.5. Mean: 43.9. Range: 85.
3. Mode: No mode. Median: 46. Mean: 43.571. Range: 61.
4. Mode: No mode. Median: 17. Mean: 18. Range: 28.
5. Mode: No mode. Median: 10.5. Mean: 13.5. Range: 27.
6. Mode: 15. Median: 22.5. Mean: 25.857. Range: 31.
B.
7. Mode: 4.3. Median: 4.2. Range: 2.1.
8. Mode: 18.6. Median: 18.6. Range: 0.8.
C.
9. Mode: No mode. Median: 4/9.
10. Mode: No mode. Median: 5/24.
2x + 8 > -4. 2.find the solution set of x and express the solutions set in number form
Answers
The solution set of this inequality is {x| x > -6.1}
How to find the solution set?Here we have the inequality:
2x + 8 > -4.2
To find the solution set, we need to isolate the variable x in one of the sides of the inequality. Doing that we will get:
2x + 8 > -4.2
2x > -4.2 - 8
2x > -12.2
x > -12.2/2
x > -6.1
So the set of all numbers larger than -6.1, this in number form is:
{x| x > -6.1}
Learn more about inequalities at.
https://brainly.com/question/24372553
#SPJ1
BRAINLIEST + 20 POINTS!!! plz help
Use the graph to answer the questions on this quiz.
Over which of the following approximate interval(s) is the water level decreasing?
Choose the correct answer(s).
A. 0 < x < 4
B. 10 < x < 16
C. 6 < x < 10
D. 4 < x < 6

Answers
Answer:
d
Step-by-step explanation:
which table represents a function

Answers
Answer:
The last one
Step-by-step explanation:
A function is where every x has only one y value.
How do you Simplify 4c+c+6c
Answers
Answer:
11c
Step-by-step explanation:
They are like terms meaning they all have the same variable you can just add them.
4c+c+6c
11c
Answer:
11c
Explanation:
We are given the expression:
4c+c+6c
We can simplify by combining like terms. All three terms have a “c” so they can all be combined.
Factor out a “c” and add the coefficients.
4c+1c+6c
(4+1+6)c
(11)c
11c
4c+c+6c simplified is 11c