Give an example of a function that is everywhere continuous

Answer:

j=76 and k=65

Step-by-step explanation:

\(j + k = 141 \\ 7x + 13 + 83 + - 2x = 141 \\ 96 + 5x = 141 \\ 5x = 141 - 96 \\ 5x = 45 \\ x = \frac{45}{5} \\ x = 9 \\ j = (7 \times 9 + 13) \\ j =76 \\ k = 83 - 2(9) \\ = 83 - 18 \\ = 65\)

Without explicitly solving for x, we can conclude that the solution to the equation 2^x - 2 = 8^4 is x = 12.

To solve the equation 2^x - 2 = 8^4 without explicitly solving for x, we can simplify the equation using exponent rules and observe the relationship between the numbers.

First, let's simplify the equation:

2^x - 2 = 8^4

We know that 8 can be expressed as 2^3, so we can rewrite the equation as:

2^x - 2 = (2^3)^4

Applying the exponent rule (a^m)^n = a^(mn), we can simplify further:

2^x - 2 = 2^(34)

Simplifying the right side of the equation:

2^x - 2 = 2^12

Now, we can observe that both sides of the equation have the same base, which is 2. In order for the equation to hold true, the exponents must be equal:

x = 12

Therefore, we may deduce that the answer to the equation 2x - 2 = 84 is x = 12 without having to explicitly solve for x.

for such more question on equation

https://brainly.com/question/17482667

#SPJ8

Answer:

no solutions

Step-by-step explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

equation of blue line is y = x + 2 , in slope- intercept form

with slope m = 1

equation of red line is y = x - 3 , in slope- intercept form

with slope m = 1

• Parallel lines have equal slopes

then the blue and red lines are parallel.

the solution to the system is at the point of intersection of the 2 lines

since the lines are parallel then they do not intersect each other.

thus the system shown has no solution.

Answer:

\(P(Cable\ TV\ only) = 50\%\)

\(P(Internet\ |\ cable\ TV) = 31.25\%\)

\(P(exactly\ 2\ services) = 23\%\)

\(P(Internet\ and\ cable\ TV \only) = 23\%\)

Step-by-step explanation:

Given

\(Cable\ TV = 80\%\)

\(Internet = 44\%\)

\(Telephone = 29\%\)

\(Cable\ TV\ and\ Internet = 25\%\)

\(Cable\ TV\ and\ Telephone = 20\%\)

\(Internet\ and\ Telephone = 23\%\)

\(All\ Services = 15\%\)

Solving (a): A) P(cable TV only).

First, we calculate n(cable TV only)

This is calculated as:

\(n(cable\ TV\ only) = (Cable\ TV) - (Cable\ TV\ and\ Internet) - (Cable\ TV\ and\ Telephone) + (All\ Services)\)

\(n(cable\ TV\ only) = 80\% - 25\% - 20\% + 15\%\)

\(n(cable\ TV\ only) = 50\%\)

The probability is:

\(P(Cable\ TV\ only) = \frac{n(Cable\ TV\ only)}{100\%}\)

\(P(Cable\ TV\ only) = \frac{50\%}{100\%}\)

\(P(Cable\ TV\ only) = 50\%\)

Solving (b): P(Internet | cable TV).

This is calculated as:

\(P(Internet\ |\ cable\ TV) = \frac{Cable\ TV\ and\ Internet}{Cable\ TV}\)

\(P(Internet\ |\ cable\ TV) = \frac{25\%}{80\%}\)

\(P(Internet\ |\ cable\ TV) = \frac{25}{80}\)

\(P(Internet\ |\ cable\ TV) = 31.25\%\)

Solving (c): P(exactly 2 services).

This is calculated as:

\(P(exactly\ 2\ services) = (Cable\ TV\ and\ Internet - All) + (Cable\ TV\ and\ Telephone - All) + (Internet\ and\ Telephone - All)\)

\(P(exactly\ 2\ services) = (25\% - 15\%) + (20\% - 15\%) + (23\%-15\%)\)

\(P(exactly\ 2\ services) = (10\%) + (5\%) + (8\%)\)

\(P(exactly\ 2\ services) = 23\%\)

Solving (d): P(Internet and cable TV only).

This is calculated as:

\(P(Internet\ and\ cable\ TV \only) = \frac{(Internet\ and\ cable\ TV \only)}{100\%}\)

\(P(Internet\ and\ cable\ TV \only) = \frac{23\%}{100\%}\)

\(P(Internet\ and\ cable\ TV \only) = \frac{23\%}{1}\)

\(P(Internet\ and\ cable\ TV \only) = 23\%\)

Answer:r=2 cos^4(theta)

Step-by-step explanation:To find the values of theta where the maximum r-values occur on the graph of the polar equation r = 2 cos^4(theta), we need to find where the derivative of r with respect to theta is equal to zero, since the maximum r-values occur at these points.

First, we can simplify the equation by using the identity cos(2theta) = 2cos^2(theta) - 1 and substituting cos^2(theta) = (1 + cos(2theta))/2. This gives:

r = 2 cos^4(theta) = 2(1/2 + 1/2 cos(2theta))^2 = 1 + cos(2theta) + cos^2(2theta)/2.

Next, we can take the derivative of r with respect to theta, using the chain rule:

dr/dtheta = -sin(2theta) - 2cos(2theta)sin(2theta).

Setting this equal to zero and factoring out sin(2theta), we get:

sin(2theta)(-1 - 2cos(2theta)) = 0.

This equation is satisfied when sin(2theta) = 0 or cos(2theta) = -1/2.

When sin(2theta) = 0, we have 2theta = k*pi for some integer k. Therefore, theta = k*pi/2.

When cos(2theta) = -1/2, we have 2theta = 2*pi/3 + 2*k*pi or 2theta = 4*pi/3 + 2*k*pi for some integer k. Therefore, theta = pi/3 + k*pi or theta = 2*pi/3 + k*pi.

These are the values of theta where the maximum r-values occur on the graph of the polar equation r = 2 cos^4(theta).

The function family of f(x) = 5x - 2 is the linear function and the comparison of the graphs of y = x and f(x) = 5x - 2 is that:

The function is given as:

f(x) = 5x - 2

Linear functions are represented as:

y = mx + c

The equation f(x) = 5x - 2 take the form of a linear function.

And the parent function of a linear function is y = x

Hence, the function family of f(x) = 5x - 2 is the linear function

The comparison of the graphs of y = x and f(x) = 5x - 2 is that:

Read more about linear functions a:

https://brainly.com/question/4025726

#SPJ1

Answer:

x = 60

Step-by-step explanation:

12 divided by 20 = 0.6

60 divided by 100 = 0.6

So x = 60

Hope I helped :)

Please consider Brainliest :)

Answer:

4005

Step-by-step explanation:

3,998 - (-7) = ?

Two negative signs will make a positive sign.

3,998 - (-7) = 3998 + 7 = 4005

So, the answer is 4005

Answer:

To solve the equation:

2/3x - 1/5x = x - 1

First, we need to find a common denominator for 2/3 and 1/5, which is 15. So we can rewrite the equation as:

(10/15)x - (3/15)x = 15/15 x - 1

Simplifying the left side:

(7/15)x = 15/15 x - 1

Multiplying both sides by 15:

7x = 15x - 15

Subtracting 7x from both sides:

-8x = -15

Dividing both sides by -8:

x = 15/8 or 1.875

Therefore, the solution to the equation is x = 1.875.

Answer:

8

Step-by-step explanation:

12-10=2

10-m=2

m=8

The given values into the equation AE = 2a + 10. Therefore, The value of AE is 3 - x.

To find the value of AE, we can substitute the given values into the equation AE = 2a + 10.

Given:

AB = 10

AE = 2a + 10

ED = x + 3

CD = 4

Since AB is a segment on the line, it can be divided into AE and ED. Therefore, AB = AE + ED.

We know that AB = 10 and CD = 4. So, if we subtract CD from AB, we get AE + ED = 10 - 4.

AE + ED = 6.

Now, we can substitute the value of ED, which is x + 3, into the equation: AE + x + 3 = 6.

To find the value of AE, we need to isolate it on one side of the equation. Let's subtract x and 3 from both sides:

AE = 6 - x - 3.

Simplifying further, we get;

AE = 3 - x.

Therefore, the value of AE is 3 - x.

for such more question on value

https://brainly.com/question/27746495

#SPJ8

The first equation is incorrect.

The second equation is correct.

The third equation is correct.

Let's go through each equation and determine whether it is correct or incorrect:

(b²+7b-9)+(4b-6b²) = -8b² + 14b-9

To determine if this equation is correct, we need to simplify both sides and check if they are equal.

On the left side:

(b²+7b-9)+(4b-6b²) = b² - 6b² + 7b + 4b - 9 = -5b² + 11b - 9

On the right side:

-8b² + 14b - 9

Comparing both sides, we can see that -5b² + 11b - 9 is not equal to -8b² + 14b - 9. Therefore, the equation is incorrect.

(4a+6)-(3a²-9a+1)=-3a²+ 13a +5

Again, we need to simplify both sides of the equation and check if they are equal.

On the left side:

(4a+6)-(3a²-9a+1) = 4a + 6 - 3a² + 9a - 1 = -3a² + 13a + 5

On the right side:

-3a² + 13a + 5

Comparing both sides, we can see that -3a² + 13a + 5 is equal to -3a² + 13a + 5. Therefore, the equation is correct.

(12c-8c²)+(5c²- 10c) = -3c²+2c

Again, let's simplify both sides and compare them.

On the left side:

(12c-8c²)+(5c²- 10c) = 12c - 8c² + 5c² - 10c = -3c² + 2c

On the right side:

-3c² + 2c

Comparing both sides, we can see that -3c² + 2c is equal to -3c² + 2c. Therefore, the equation is correct.

For more such questions on equation visit:

https://brainly.com/question/17145398

#SPJ8

Answer:

1) B. at 0 and 3 only

2) D. 2eˣcosx

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

Algebra I

Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

Derivative Property [Addition/Subtraction]:                                                          \(\displaystyle \frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}[f(x)] + \frac{d}{dx}[g(x)]\)

Derivative Rule [Product Rule]:                                                                              \(\displaystyle \frac{d}{dx} [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)\)

Trig Derivative: \(\displaystyle \frac{d}{dx}[sinu] = u'cosu\)

Trig Derivative: \(\displaystyle \frac{d}{dx}[cosu] = -u'sinu\)

eˣ Derivative: \(\displaystyle \frac{d}{dx} [e^u]=e^u \cdot u'\)

Step-by-step explanation:

*Note:

Velocity is the derivative of position.

Acceleration is the derivative of velocity.

Question 1

Step 1: Define

s(t) = t⁴ - 6t³ - 2t - 1

Step 2: Differentiate

Step 3: Solve

Question 2

Step 1: Define

f(x) = eˣ(sinx + cosx)

Step 2: Differentiate

Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives

Book: College Calculus 10e

Answer:

The cost of printing 142 more posters when 18 has already been printed is $5.57.

Step-by-step explanation:

We are given that the marginal cost (dollars) of printing a poster when x posters have been printed is given by the following equation C'(x)=x^-3/4.

The given equation is: \(C'(x) = x^{\frac{-3}{4} }\)

The cost of printing 142 more posters when 18 have already been printed is given by;

Integrating both sides of the equation and using the limits we get;

\(\int_{a}^{b} C'(x) dx=\int_{18}^{142} x^{\frac{-3}{4}}dx\)

As we know that  \(\int\limits {x}^{n} \, dx = \frac{x^{n+1} }{n+1}\) , so;

          =  \(\frac{x^{\frac{-3}{4}+1 } }{\frac{-3}{4}+1 } ]^{142} __1_8\)

          =  \(\frac{x^{\frac{1}{4} } }{\frac{1}{4} } ]^{142} __1_8\)

          =  \(4[x^{\frac{1}{4} } } ]^{142} __1_8\)

          =  \(4[(142)^{\frac{1}{4} }- (18)^{\frac{1}{4} }} ]\)

          =  $5.57

Hence, the cost of printing 142 more posters when 18 has already been printed is $5.57.

Answer:

I'm sorry but I couldn't see the hole question

The output value of (g/f)(x) is 9x/(7x + 28).

The domain of g/f is (-∞, -4) U (-4, ∞)..

In this exercise, we would determine the corresponding composite function of f(x) and g(x) under the given mathematical operations in simplified form as follows;

(g/f)(x) = (9/(x + 4)) ÷ 7/x

By rearranging the mathematical expression using the multiplication operation, we have the following:

(g/f)(x) = (9/(x + 4)) × x/7

(g/f)(x) = 9x/(7x + 28)

For the restrictions on the domain, we would have to equate the denominator of the rational function to zero and then evaluate as follows;

7x + 28 ≠ 0

7x ≠ -28

x ≠ -4

Domain = (-∞, -4) U (-4, ∞).

Read more on domain here: brainly.com/question/17440903

#SPJ1

Answer:

Step-by-step explanation:

Answer:

-18

Step-by-step explanation:

-27+9=-18

Answer:

2x-3y<-9

Step-by-step explanation:

Answer:

Step-by-step explanation:

The compound interest is represented by the following equation:

Therefore, for:

1. P=$4,000, t=7 years at r=6%

2. P= $5,000, t=20 years at r=5%

3. P=$700, t=15 years at 7%, n=2

Answer: It should be 1/10 :)

By performing the division, the jogging track is 0.45 miles long.

Division is a mathematical operation that involves the splitting of a quantity into equal parts or groups.

The problem asks us to convert a length of 792 yards to miles. To do this, we need to use a conversion factor to relate yards to miles. We know that there are 1760 yards in a mile, so we can use this relationship to convert the length in yards to miles.

To convert yards to miles, we divide the length in yards by the number of yards in a mile. This is because we want to cancel out the units of yards and be left with the corresponding number of miles.

So, 792 yards / 1760 yards/mile gives us the length of the jogging track in miles. We can simplify this expression by performing the division to get the result of 0.45 miles. Therefore, the jogging track is 0.45 miles long.

To know more about division visit:

https://brainly.com/question/28119824

#SPJ1

Answer:

  \(a=\dfrac{\Delta v}{t}\)

Step-by-step explanation:

Acceleration is the change in velocity per unit time. It is usually represented by the letter "a". An appropriate formula is ...

  \(\boxed{a=\dfrac{\Delta v}{t}}\)

The required equation for determining the acceleration from a velocity-time graph is \(a=\dfrac{\Delta v}{t}\)equation is a=delta v over t.

We know that,

Acceleration is known as the rate of change of velocity per unit time.

The velocity vs time graph is the graph plotted between the change in velocity with the change in time.

\(a=\dfrac{\Delta v}{t}\)

Hence the required equation for determining the acceleration from a velocity-time graph is \(a=\dfrac{\Delta v}{t}\).

For more details on Acceleration follow the link:

https://brainly.com/question/3072589

Answer:

my answer is negative 14/3.

Step-by-step explanation:

choice A hope that helps you if I'm wrong please tell me the right answer right away I can try another method.

The standard deviation of the sampling distribution of the mean is d)3.75; the distribution is approximately Normal.

According to the Central Limit Theorem, when the sample size is large enough (typically n > 30), the sampling distribution of the mean will be approximately normal, regardless of the shape of the population distribution.

In this case, the sample size is 16, which is larger than 30, so we can assume that the sampling distribution of the mean is approximately normal.

The standard deviation of the sampling distribution of the mean (also known as the standard error) is given by:

σm = σ/ √n

where σ is the population standard deviation and n is the sample size.

Plugging in the given values:

σm = 15/ √16 = 15/4 = 3.75

So the standard deviation of the sampling distribution of the mean for the student's sample is 3.75 minutes.

For more questions like Sampling distribution click the link below:

https://brainly.com/question/13501743

#SPJ4

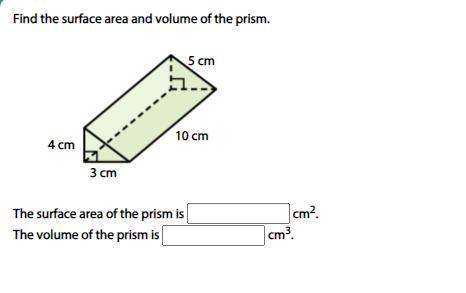
Answer:

Surface area: 92 cm2

Volume: 60 cm3

Step-by-step explanation:

Hope this helps and tell me in the comments if it is correct or not.

Answer:

f(1·2)

Step-by-step explanation:

Subbing x=1 (f(1)) into the original function f(x)=a^x will give f(1)=a^1 which is simply equal to a. Therefore, if we were to do [f(1)]^2, we would just get a^2 because f(1) is equivalent to a. Out of the choice.s present, only f(1·2) is equal to a^2, because a^(1·2)=a^2