g 6. what can you conclude based on the results of your test (hint: what does the p-value tell you?)? do you reject the null hypothesis, or fail to reject the null hypothesis? does the chis sample population have a statistically significant different average height than 68 inches tall?
Answers
The sample population has a statistically significant different average height than 68 inches tall. In general, the p-value is a measure of the strength of evidence against the null hypothesis.
A small p-value (typically less than 0.05) indicates strong evidence against the null hypothesis, while a large p-value (greater than 0.05) indicates weak evidence against the null hypothesis. If the p-value is less than the specified significance level (e.g., 0.05), then the null hypothesis is typically rejected in favor of the alternative hypothesis.
Without more information about the statistical test and the results, it is not possible to determine whether the null hypothesis should be rejected or not, or whether the sample population has a statistically significant different average height than 68 inches tall.
Learn more about " null hypothesis" : https://brainly.com/question/4436370
#SPJ11
Related Questions
Which types of life experiences have shaped your identity?
Answers
Please please help me with this question please now please

Answers
Answer with Step-by-step explanation:
Regular price=$39.79
Rounded price=$40
Discount percent=25%
Estimated Discount=25% of $40
$10
Estimated sale price= $40-$10
$30
Michael starts a website for people in his town to share news and photos. Before launching the website, he has his friends and family sign up. Then, he uses the equation shown to estimate the number of users, y, who will have signed up x weeks after he officially launches the website.
Answers
Answer:
u fking b
ur bad
How many solutions does this equation half? x=x+9
Answers
Answer:
I think it is 0 solutions
Step-by-step explanation:
it should be 0 because no matter what number you substitie x for, the right side will always be 9 higher than it, so x never equals x
May I have brainliest please? :)
Kevin earns $5 per hour at an ice rink. Which graph best represents Kevin's total earnings over time?
Answers
Answer:
If he earns 5$ an hour then just multiply how long he works over time by 5 and you get you answer C: for ex: if he worked 24h he would get 120$ because 24 x 5=120
Step-by-step explanation:
a conical water tank with vertex down has a radius of 12 feet at the top and is 26 feet high. if water flows into the tank at a rate of 10 ft3/min, how fast is the depth of the water increasing when the water is 13 feet deep?
Answers
The depth of the water increasing when the water is 13 feet deep is approximately 1.68 feet per minutes.
We know that the conical water tank has a radius of 12 feet and is 26 feet high.
We also know that water is flowing into the tank at a rate of 30ft³/min. In other words, our derivative of the volume with respect to time t is:
\(\frac{dV}{dt} = \frac{10 ft^3}{min}\)
We want to find how fast the depth of the water is increasing when the water is 13 feet deep. So, we want to find dh/ dt.
First, remember that the volume for a cone is given by the formula:
V = 1/3 π r² h
We want to find dh/dt. So, let's take the derivative of both sides with respect to the time t. However, first, let's put the equation in terms of h.
We can see that we have two similar triangles. So, we can write the following proportion:
\(\frac{r}{h} = \frac{12}{36}\)
Multiply both sides by h:
⇒ \(r = \frac{12}{36} h\)
So, let's substitute this in r:
\(V = \frac{1}{3} \pi \frac{12}{36} h^{2} h\)
Square:
\(V = \frac{1}{3} \pi \frac{144}{3888} (h^{2} ) h\)
Simplify:
\(V = \frac{144}{3888} \pi h^{2}\)
Now, let's take the derivative of both sides with respect to t:
\(\frac{d}{dt} (V) = \frac{d}{dt} [\frac{144}{3888} ] \pi h^{3}\)
Simplify:
\(\frac{dV}{dt} =\frac{144}{3888} \pi (3h^{2} ) \frac{dh}{dt}\)
We want to find dh/dt when the water is 13 feet deep. So, let's substitute 13 for h. Also, let's substitute 10 for dV/dt. This yields:
\(10 = \frac{144}{3888} \pi (3(13^{2} ) \frac{dh}{dt}\)
\(10 = \frac{144}{3888} \pi (507) \frac{dh}{dt}\)
\(10 = \frac{73008}{3888} \pi \frac{dh}{dt}\)
\(38880 = 73008 \pi \frac{dh}{dt}\)
\(\frac{dh}{dt} = \frac{38880}{73008} \pi\)
\(\frac{dh}{dt} = \frac{38880}{73008} X\frac{22}{7}\)
≈ 1.6737109 feet / min
The water is rising at a rate of approximately 1.68 feet per minute.
Learn more about depth:
https://brainly.com/question/13804949
#SPJ4
For your speech to be effective, you must carefully consider what your specific _____________ is. a. purpose b. audience c. thesis d. research Please select the best answer from the choices provided A B C D
Answers
Answer: A, Purpose
Step-by-step explanation: Nothing else makes sence In the sentence, and certain purpose makes you have a goal, which matches up with a speech being effective.
Answer: The correct answer is a. purpose
Step-by-step explanation:
What is the solution to the equation 5 (x minus 6) = 2 (x 3)? x =
Answers
the solution to the equation is x=12
The distributive property is defined as
Let us now solve the equation.
5(x - 6) = 2(x + 3)
Using the distributive property, simplify the parentheses on both sides.
5(x - 6) = 2(x + 3)
5x - 30 = 2x + 6
The parenthesis was simplified. However, we have one x term on one side and another x term on the other.
5x - 30 - 2x = 2x + 6 - 2x
3x - 30 = 6
We only have an x term on one side of the equation now.
To begin, reverse the subtraction by adding 30 to either side of the equation.
To keep an equation balanced or true, we do the identical operation on both sides.
3x - 30 + 30 = 6 + 30
3x = 36
We're getting close to an answer. Only one more step.
The x term is multiplied by 3.
We can undo the multiplication operation by dividing both sides by 3.
3x / 3 = 36 / 3
x = 12
So, x is equal to 12.
Learn more about Equations here: https://brainly.com/question/2972832
#SPJ4
This question requires TWO checkboxes to complete. Alex is building the fraction moted below to find the product of the experim 325 one-whole 4 1 ! d 공 중 중 1 a ! 1 6 중 Select the option that correctly completes each statement A 3 Alex can find the product by shading B 5 6 sections in each row. 2 6 15 The product of the expression 3 xãi is 6 f 15 풍 6 E. 75/6
Answers
Alex can find the product by shading 5 sections in each row. In this way, each shaded row represents 5/6.
Now, to find the product, Alex has to add the shaded values, that is,
\(\frac{5}{6}+\frac{5}{6}+\frac{5}{6}=\frac{5+5+5}{6}=\frac{15}{6}\)Determine if the following statement is true or false. The population will be normally distributed if the sample size is 30 or more. The statement is false
Answers
Answer: False
Step-by-step explanation: It literally says false.
The statement "The population will be normally distributed if the sample size is 30 or more" is false.
A normal distribution is a probability distribution that is bell-shaped and symmetrical around the mean. When we measure a characteristic of a large population, such as the height of adult men in the United States, the distribution of those measurements follows a normal distribution. The normal distribution is used to model a wide range of phenomena in fields like statistics, finance, and physics.
Sample size is the number of observations in a sample. The larger the sample size, the more reliable the results, which is why researchers typically aim for large sample sizes.
Therefore, it is false to say that if the sample size is 30 or more, the population will be normally distributed.
To know more about normal distribution please visit:
https://brainly.com/question/23418254
#SPJ11
what are the odds of randomly generating an even number with the first two odd numbers and unique numbers
Answers
The odds of randomly generating an even number with the first two odd numbers and unique numbers = \(\frac{10}{16}= \frac{5}{8}\).
Sum will be even if either both numbers are odd or both numbers are even .
So, Total no. of way to select numbers for making sum even
= 5C2 + 4C2 = 10 + 6 = 16
And, Total numbers of ways to select two odd numbers such that sum is even = 5C2 = 10
Probability that both numbers are odd = \(\frac{10}{16}= \frac{5}{8}\)
Hence the answer is the odds of randomly generating an even number with the first two odd numbers and unique numbers = \(\frac{10}{16}= \frac{5}{8}\).
To learn more about probability click here https://brainly.com/question/25870256
#SPJ4
Explain the statement. "All functions are relation but some relations are not functions?"
Answers
Answer:
This is because, a relation could be any set of ordered pairs where as a function is a set of ordered pairs where there is only ONE value of y for every value of x.
Another way of explaining it is:
In fact, every function is a relation. However, not every relation is a function. In a function, there cannot be two lists that disagree on only the last element. This would be tantamount to the function having two values for one combination of arguments. By contrast, in a relation, there can be any number of lists that agree on all but the last element.
The statement "All functions are relations but some relations are not functions" highlights the relationship between functions and relations and the distinction between the two concepts.
In mathematics, a relation is a set of ordered pairs that establishes a connection between elements of two sets. It can be thought of as a collection of inputs and outputs.
On the other hand, a function is a specific type of relation in which each input value (x-coordinate) is associated with exactly one output value (y-coordinate).
So, when we say "all functions are relations," we are acknowledging that functions are a subset of relations. This is because functions satisfy the property of assigning a unique output for each input, making them a special kind of relation.
However, the statement also recognizes that there are relations that do not meet the criteria of a function. This occurs when an input value is associated with multiple output values or when an input value has no corresponding output value.
In other words, some relations may have more than one output value for a given input, or they may lack a well-defined output for certain inputs. Such relations are not considered functions.
Therefore, while all functions can be classified as relations, not all relations can be classified as functions due to the specific requirement of having a unique output for each input.
To know more about functions refer here:
https://brainly.com/question/31062578
#SPJ11
2) Graph the system of inequalities
y > -2x + 1
y≤ x + 3

Answers
Translate this to english
Por favor ayúdame, no puedo tener constante y> -2x + 1
y≤ x + 3 caca es 6 pies arriba en la jaula de mi perro
Find the difference-5.6-(4.8-11.1)
Answers
Answer: 0.7
Step-by-step explanation: hope it helps
Answer:
0.7
Step-by-step explanation:
0.7
In a class, the ratio of girls to boys is 3:1
There are 18 girls in the class.
How many boys are there?
Answers
The number of boys in the class can be found by finding the solution of equation as 6.
How to write a linear equation?A linear equation for the given case can be written by assuming any variable as the unknown quantity. Then, as per the given data the required operations are done and it is equated to some value.
The ratio of boys and girls are given as 3 : 1.
As per the question the number of girls are 18.
Suppose, the number of boys be x.
Then, the following equation can be written as,
3/1 = 18/x
⇒ x = 18/3
⇒ x = 6
Hence, the number of boys in the class is given as 6.
To know more about linear equation click on,
https://brainly.com/question/11897796
#SPJ2
Pls help solve the equation

Answers
Answer:
34 boxes
Step-by-step explanation:
Please see attached picture for full solution.

3. Liquid is being poured into the top of a funnel at a steady rate of 200 cm3/s. The funnel in the shape
of an inverted cone with a radius equal to its height. There is has a small hole in the bottom where the
liquid is flowing out at a rate of 20 cm3/s. How fast is the height of the liquid changing when the liquid
in the funnel is 15 cm deep?
At the instant when the height of the liquid is 25cm, the funnel becomes clogged at the bottom and no
more liquid flows out. How fast does the height of the liquid change just after this occurs?
Answers
Just after the funnel is clogged height of the liquid remains constant at 25 cm
The given problem can be solved by differentiating and integrating the cone formulas and then applying the concept of related rates.
We will also need to use the concept of similar triangles.Let's solve the given problem -1. At 15 cm deep, the radius and height of the cone can be found as follows
We have a cone with radius r and height h.
The radius of the cone is equal to its height.
So,r = h
Volume of the cone,
V = (1/3)πr²h
⇒ V = (1/3)πh²h
⇒ V = (1/3)πh³
Since the liquid is being poured into the cone at a steady rate of 200 cm³/s, the volume of liquid in the cone is given by
V = 200t cm³ where t is the time in seconds.
Volume of the liquid at height 15 cm
Using similar triangles, we can write,
(h - 15)/h = r/R
⇒ r = (h/2)
At height h = 15 cm, radius r = h/2 = 7.5 cm
Volume of the liquid at height 15 cm = (1/3)π(7.5)²(15 - 0) cm³
= 1767.85 cm³
The volume of the liquid that has flowed out through the hole in the bottom of the cone is given by
V = 20t cm³
Equating the two volumes, we get
200t = 1767.85 + 20t
⇒ t = 8.83925 s
Differentiating the equation V = (1/3)πh³ with respect to time t, we get
dV/dt = πh² dh/dt
At the instant when the height of the liquid is 15 cm, the height of the cone is also 15 cm.
Therefore, at this instant, the rate of change of volume of the liquid with respect to time is
dV/dt = 200 cm³/s
We need to find the rate at which the height of the liquid is changing, i.e., dh/dt when h = 15 cm.
Using the relation,dV/dt = πh² dh/dt
we get, dh/dt = (dV/dt) / (πh²)
⇒ dh/dt = (200) / (π(15)²) cm/s
⇒ dh/dt = 0.02856 cm/s
So, the height of the liquid is increasing at a rate of 0.02856 cm/s when the liquid in the funnel is 15 cm deep.
2. At 25 cm deep, the radius and height of the cone can be found as follows
Using similar triangles, we can write,
(h - 25)/h = r/R
⇒ r = (h/3)
At height h = 25 cm, radius r = h/3 = 8.333 cm
Volume of the liquid at height 25 cm = (1/3)π(8.333)²(25 - 0) cm³
= 1458.33 cm³
Since the funnel becomes clogged at the bottom when the height of the liquid is 25 cm, the volume of liquid in the cone remains constant at 1458.33 cm³.
Differentiating the equation V = (1/3)πh³ with respect to time t, we get
dV/dt = πh² dh/dt
At the instant when the height of the liquid is 25 cm, the rate of change of volume of the liquid with respect to time is
dV/dt = 0
We need to find the rate at which the height of the liquid is changing just after the funnel gets clogged.i.e., dh/dt when h = 25 cm and dV/dt = 0.
From the equation,dV/dt = πh² dh/dt
we get,
dh/dt = (dV/dt) / (πh²)
⇒ dh/dt = 0 cm/s
Therefore, just after the funnel gets clogged, the height of the liquid remains constant at 25 cm.
Learn more about height of the liquid from the given link
https://brainly.com/question/29730559
#SPJ11
Kevin drew a scale drawing of a house. The scale he used was 1 millimeter : 4 meters. If the actual length of the living room is 8 meters, how long is the living room in the drawing?
Answers
If the actual length of the living room is 8 meters, according to the scale drawing living room in the sketching should be 2 millimeters
What is the scale drawing?Scale drawings are images that depict objects at a scale different from their actual size. Depending on the size of the object being represented and how the sketching will be used, they can depict objects at either a bigger or smaller scale than full size. The scale gives the proportion of a distance at full size to the distance that, at the scale in use, would have the same length.
Scale drawings are used to illustrate objects when sketching them at their true scale would not be practical or beneficial. This could be because depicting the object as its whole would be difficult or difficult to fit on a single sheet of paper.
since 4meter = 1mm
then 8meter = 2mm
To learn more about scale of drawing from the given link
https://brainly.com/question/17388747
#SPJ1
The test scores for a class of 163 students are computed. What is the location of the test score associated with the third quartile
Answers
The location of the test score associated with the third quartile is the value that corresponds to the 123rd rank in a class of 163 students.
The third quartile, also known as the upper quartile, is a statistical measure that divides a set of data into quarters. It is the point at which 75% of the data lies below it and 25% of the data lies above it. To find the location of the test score associated with the third quartile, we need to arrange the test scores in ascending order and then find the value that corresponds to the 75th percentile.
Given that there are 163 students in the class, we can determine the rank of the score associated with the third quartile as follows:
Rank of the third quartile = 0.75 x 163 = 122.25
Since we cannot have a fractional rank, we need to round up to the next whole number. Therefore, the rank of the score associated with the third quartile is 123.
Next, we need to find the value of the test score that corresponds to the 123rd rank. We can do this by using a percentile rank calculator or by manually counting the test scores from the lowest to the highest until we reach the 123rd score.
In summary, the location of the test score associated with the third quartile in a class of 163 students is the value that corresponds to the 123rd rank.
To know more about test score, refer to the link below:
https://brainly.com/question/28559172#
#SPJ11
Use an iterated integral to find the area of the region bounded by the graphs of the equations. y=10x−x ^2 ,y=x ^2 −4x
Answers
The iterated integral to find the area is:\[A = \int_{0}^{3} \int_{x^2 - 4x}^{10x - x^2} dy \, dx\]
To find the area of the region bounded by the graphs of the equations \(y = 10x - x^2\) and \(y = x^2 - 4x\), we can set up an iterated integral.
First, let's find the x-values at which the two curves intersect. Setting the equations equal to each other, we have:
\[10x - x^2 = x^2 - 4x\]
Simplifying:
\[2x^2 - 6x = 0\]
Factoring out an x:
\[x(2x - 6) = 0\]
So we have two solutions: x = 0 and x = 3. These are the x-values where the curves intersect.
To set up the iterated integral, we need to determine the limits of integration for both x and y.
For x, the limits of integration will be from x = 0 to x = 3, as these are the x-values where the curves intersect.
For y, the limits will be determined by the equations of the curves. The lower curve is \(y = x^2 - 4x\) and the upper curve is \(y = 10x - x^2\). Therefore, the limits for y will be from y = \(x^2 - 4x\) to y = \(10x - x^2\).
The iterated integral to find the area is:
\[A = \int_{0}^{3} \int_{x^2 - 4x}^{10x - x^2} dy \, dx\]
Evaluating this iterated integral will give us the area of the region bounded by the two curves.
Learn more about equation here:brainly.com/question/29657983
#SPJ11
If Tai Reed's average monthly expenditure for 4 months is $2,303.50, what is the total of his expenditures for that period? *
685.75
575.85
9,214.00
12,545.50
TIMEDD TEST!!
Answers
Answer : $9,214.00
(12x -2) - (-3x + 4) anyone got the answer?
Answers
Answer:
15x - 6
Step-by-step explanation:
(12x -2) -1 (3x+4)
(12x - 2 + 3x-4
12x-2+3x -4
12x -6 + 3x
15x - 6
Make r the subject of the formula t = r
_
r - 3

Answers
We will try to leave the letter \(r\) alone by modifying the given equation.
\(t=\frac{r}{r-3}\)\(\frac{1}{t}=\frac{r-3}{r}\)\(\frac{1}{t}=1-\frac{3}{r}\)\(\frac{1}{t}-1=-\frac{3}{r}\)\(1-\frac{1}{t}=\frac{3}{r}\)\(\frac{1}{3}-\frac{1}{3t}=\frac{1}{r}\)\((\frac{t-1}{3t} )^{-1}=(\frac{1}{r} )^{-1}\)\(\frac{3t}{t-1}=r\)This equation is defined with the following expressions.
\(t\neq 1\)\(r\neq 3\)Ans: \(r=\frac{3t}{t-1}\)
Provide an example and explain the steps to convert a fraction into a percent.
Answers
The most appropriate choice for percentage and fraction will be given by-
The process of conversion of fraction to percentage has been explained.
What is fraction and percentage?
Suppose there is a whole collection of objects and some parts of the objects are taken from the whole collection. Fraction represents those parts which are taken. In other words, part of a whole is called fraction. The upper part of the fraction is the numerator and the lower part of the fraction is the denominator.
If a number is taken as fraction of 100 then the fraction is known as percentage.
To convert a fraction into percentage, we have to simply multiply the fraction with 100.
For example.
Suppose we have a fraction \(\frac{1}{4}\), we need to convert \(\frac{1}{4}\) to percentage.
So on multiplying \(\frac{1}{4}\) by 100, we obtain = \(\frac{1}{4} \times 100\) = 25%
So, \(\frac{1}{4}\) is equivalent to 25%
To learn more about fraction and percentage, refer to the link -
https://brainly.com/question/317717
#SPJ9
A triangle is defined by the three points =(3,10), =(6,9), and =(5,2).A=(3,10), B=(6,9), and C=(5,2). Determine all angles theta, theta, and thetaθA, θB, and θC in the triangle. Give your answer in radians.
(Use decimal notation. Give your answers to three decimal places.)
Answers
The angles of the triangle is :
A = 0.506 , B = 3.692 and C = 1.850
We have the following information is:
A triangle is defined by the three points A=(3,10), B=(6,9), and C=(5,2).
We have to find the:
Determine all angles theta, theta, and thetaθA, θB, and θC in the triangle.
Now, According to the question:
The first thing we need to do, is find the length of the sides a , b and c. We can do this by using the Distance Formula.
The Distance Formula states, where d is the distance, that:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
So,
\(a=\sqrt{(6-5)^2+(9-2)^2}\)\(=\sqrt{50}\)
\(b=\sqrt{(3-5)^2+(10-2)^2} =\sqrt{66}\)
\(c=\sqrt{(6-3)^2+(9-10)^2}=\sqrt{10}\)
We now know all 3 sides, but since we don't know any angles, we will have to use the Cosine Rule.
The Cosine Rule states that:
\(a^2=b^2+c^2-2bc.cos(A)\)
Plug all the values:
\((\sqrt{50} )^2=(\sqrt{66} )^2+(\sqrt{10} )^2-2(\sqrt{66} )(\sqrt{10} ).cosA\)
50 = 66 + 10 -2\(\sqrt{66}.\sqrt{10} cosA\)
cos (A) = 50-66-10/ -2\(\sqrt{66}.\sqrt{10}\)
cos (A) = 13/25.69
A = \(cos ^ -^1 \, (cos(A))=cos^-^1\)(13/25.69) = 0.506
We rearrange the formula for angle B.
\(b^2=a^2+c^2-2bc.cos(A)\)
Angle B:
\((\sqrt{66} )^2=(\sqrt{50} )^2+(\sqrt{10} )^2-2(\sqrt{66} )(\sqrt{10} ).cosA\)
66 = 50 + 10 -2\(\sqrt{66}.\sqrt{10} cosA\)
cos (A) = 66 -50 -10/ -2\(\sqrt{66}.\sqrt{10}\)
cos(A) = 6/ -2\(\sqrt{66}.\sqrt{10}\)
cos(A) = 3.692
A = \(cos ^ -^1 \, (cos(A))=cos^-^1\)3.692
Angle C:
\(\pi -(\frac{\pi }{4} +0.506)\) = 1.850
The angles of the triangle is :
A = 0.506 , B = 3.692 and C = 1.850
Learn more about Triangle at:
https://brainly.com/question/2773823
#SPJ4
I need a good joke :D
Answers
Answer:
My life
Step-by-step explanation:
explanation: none needed
Find the value of x.
A. 4
B. 8√2/2
C. 4√2
D. 8√2
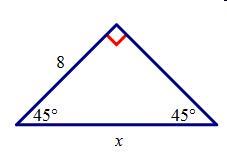
Answers
\( \sin(45) = \frac{opposite}{hypotenuse \\ } \\ \\ \sin(45) = \frac{8}{x} \\ \frac{ \sqrt{2} }{2} = \frac{8}{x} \\ x \sqrt{2} = 16 \\ \frac{x \sqrt{2} }{ \sqrt{2} } = \frac{16}{ \sqrt{2} } \\ x = \frac{16 \times \sqrt{2} }{ \sqrt{2 \times \sqrt{2} } } \\ x = \frac{16 \sqrt{2} }{2} \\ 8 \sqrt{2} \)
D is the correct answer
PLEASE GIVE BRAINLIEST
Can someone help me on this I’m confused

Answers
Step-by-step explanation:
if the goal is to have both numbers with denominator 6, then the first one is totally simple :
3 1/6 = 3 1/6
what else could it be ... ?
and the second, well, how many thirds are in a whole ?
right, 3, that's why we call them "thirds".
how many 6ths are in a whole ?
right, 6.
do you notice something ? it is easy to get from 3 to 6 by multiplying 3 by 2.
in order to keep the overall value of a fraction unchanged, when we multiply one part of the fraction by something we need to multiply the other part by the same number too.
so,
5 2/3 = 5 2/2×2/3 = 5 4/6
in short : yes, every third contains 2 6ths.
therefore, 2/3 = 4/6
What is this answer?? Please

Answers
Answer:
Linear
Step-by-step explanation:
You perform a Chi-Square test and obtain a p-value lower than 0.01. What does that mean?
Answers
Performing a Chi-Square test is a statistical tool used to determine if there is a significant difference between observed and expected data. The test helps to analyze categorical data by comparing observed frequencies to the expected frequencies. The p-value in a Chi-Square test refers to the probability of obtaining the observed results by chance alone.
If a p-value lower than 0.01 is obtained in a Chi-Square test, it means that the results are statistically significant. In other words, there is strong evidence to reject the null hypothesis, which states that there is no significant difference between the observed and expected data. This means that the observed data is not due to chance alone, but rather to some other factor or factors.
The mean, or average, is not directly related to the Chi-Square test or the p-value. The Chi-Square test is specifically used to determine the significance of the observed data. However, the mean can be used as a measure of central tendency for continuous data, but it is not applicable to categorical data.
In conclusion, obtaining a p-value lower than 0.01 in a Chi-Square test means that there is strong evidence to reject the null hypothesis, and that the observed data is statistically significant.
learn more about Chi-Square here: brainly.com/question/24976455
#SPJ11