From a survey of 100 commuters about how they get to work, 38 said they drive their cars, 47 said they take the bus, 14 said they take the subway, and 1 said they ride their bicycle. If there were 4,800 commuters total. How many drove a car out of the 4,800? How many took the bus out of the 4,800? How many took the subway of the 4,800? How many rode a bicycle out of the 4,800? PLEASE HELP
Answers
1824 drove a car
2256 take a bus
672 ride the subway
48 ride a bicycle
Related Questions
Cuál será el valor del término que ocupa el lugar 77 en la siguiente sucesión?
80, 71, 62, 53, 44, 35
Answers
Answer:
71
Step-by-step explanation:
What is the frequency of (x) = 4 sin(6 π x) +1
Answers
Answer:
Frequency is 3
Step-by-step explanation:
A sine function repeats in periods and it's frequency can be gotten using:
y(x) = sin(2πfx) where f is the frequency
We are given x = 4sin(6πx) + 1
This can be rewritten as: x = 4sin(3*2πx) + 1
Therefore, our f = 3.
Hence frequency of the sine function is 3.
2 of 6
Given that a = 12 cm and b = 17 cm, work out the area of the triangle.
Give your answer rounded to 1 DP.
Answers
Answer:
102 cm²Step-by-step explanation:
area of a triangle = 1/2 * base * height
= 1/2 * 12 * 17
= 102 cm²
ab + Bbc, a=0. b = -6, and c = 5
Answers
Answer:
180
Step-by-step explanation:
0 x -6 + -6 x -6 x 5
0 + 180 = 180
The number of degrees of freedom associated with the chi-square distribution in a test of independence is a number of populations minus number of estimated parameters minus 1. b. number of rows minus 1 times number of columns minus 1. c. number of sample items minus 1. d. number of populations minus
Answers
The correct answer to this question is option D) number of populations minus 1.
The number of degrees of freedom (df) associated with the chi-square distribution in a test of independence is determined by the number of populations from which the samples are obtained minus one.
It is calculated by the formula: df = (r - 1) x (c - 1), where r is the number of rows and c is the number of columns in the contingency table used to perform the test. The chi-square distribution is used to analyze the difference between observed and expected values in a contingency table. It provides a measure of how closely the observed frequencies match the expected frequencies if there is no association between the variables being studied.
The degrees of freedom are important because they determine the critical values for the test statistic and help to determine the probability of obtaining the observed results if the null hypothesis is true.
To know more on probability visit:
https://brainly.com/question/13604758
#SPJ11
The box plot represents the miles Emilia ran after school for 21 days.
3
4
5
9
10
6 7
8
Miles Run
Part B
Can you use the box plot to find the IQR? Explain.
Answers
This value will represent the range within which the middle 50% of Emilia's daily miles are distributed
Hi! The box plot represents the miles Emilia ran after school for 21 days. To find the IQR (Interquartile Range), you can use the box plot by identifying the values of the first quartile (Q1) and the third quartile (Q3).
The IQR is calculated by subtracting Q1 from Q3 (IQR = Q3 - Q1). By examining the box plot, locate Q1 and Q3 on the plot, and perform the subtraction to find the IQR.
This value will represent the range within which the middle 50% of Emilia's daily miles are distributed.
To know more about range refer here
https://brainly.com/question/28135761#
#SPJ11
The speed of light is about 300,000,000 meters per
second. That's about 3 * 108 meters per second. The
speed of sound in dry air is about 3 * 102 meters per
second.
Which travels faster?
Speed of Sound in Dry Air
Speed of Light
3 x 102 m/s
3 x 108 m/s

Answers
Answer: it’s speed of light
Please help ASAP!!! THANKS!

Answers
Given:
The vertices of a parallelogram GHJK are K(1,2), J(5,2), G(0,8).
To find:
The coordinate of the vertex H.
Solution:
We know that the diagonals of a parallelogram bisects each other. It means the midpoint of the diagonals are same.
Let the coordinate of the vertex H are (a,b).
Midpoint formula:
\(Midpoint=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)\)
In parallelogram GHJK ,
Midpoint of diagonal GJ = Midpoint of diagonal HK
\(\left(\dfrac{0+5}{2},\dfrac{8+2}{2}\right)=\left(\dfrac{a+1}{2},\dfrac{b+2}{2}\right)\)
\(\left(\dfrac{5}{2},\dfrac{10}{2}\right)=\left(\dfrac{a+1}{2},\dfrac{b+2}{2}\right)\)
On comparing both sides, we get
\(\dfrac{5}{2}=\dfrac{a+1}{2}\)
\(5=a+1\)
\(5-1=a\)
\(4=a\)
And,
\(\dfrac{10}{2}=\dfrac{b+2}{2}\)
\(10=b+2\)
\(10-2=b\)
\(8=b\)
Therefore, the coordinates of the vertex H are (4,8). Hence, option B is correct.
On a coordinate plane, 2 lines are shown. Line P Q has points (negative 5, 3) and (5, 1). Line R S has points (negative 4, negative 2) and (0, negative 4).
Which statement best explains the relationship between lines PQ and RS?
They are parallel because their slopes are equal.
They are parallel because their slopes are negative reciprocals.
They are not parallel because their slopes are not equal.
They are not parallel because their slopes are negative reciprocals.

Answers
Given:
Line P Q has points (-5, 3) and (5, 1).
Line R S has points (-4, -2) and (0, -4).
To find:
The relationship between lines PQ and RS.
Solution:
If a line passing through two points, then the slope of line is
\(m=\dfrac{y_2-y_1}{x_2-x_1}\)
Line P Q has points (-5, 3) and (5, 1). So, slope of line PQ is
\(m_1=\dfrac{1-3}{5-(-5)}\)
\(m_1=\dfrac{-2}{5+5}\)
\(m_1=\dfrac{-2}{10}\)
\(m_1=\dfrac{-1}{5}\)
Line R S has points (-4, -2) and (0, -4). So, slope of line RS is
\(m_2=\dfrac{-4-(-2)}{0-(-4)}\)
\(m_2=\dfrac{-4+2}{0+4}\)
\(m_2=\dfrac{-2}{4}\)
\(m_2=\dfrac{-1}{2}\)
Slopes of two parallel lines are equal.
\(m_1\neq m_2\)
They are not parallel because their slopes are not equal.
Therefore, the correct option is C.
Answer:
the correct answer is c
Step-by-step explanation:
Edu2020
simplify
(2x - 5)(x + 3) = 0
Answers
Answer:
x = 5/2, -3
or
x = 2.5, -3
or
2 1/2, -3
Step-by-step explanation:
Brainliest Please!!
- Hermionia
Answer:
x=-3, 5/2
Step-by-step explanation:
Set each parentheses equal to zero.
1. 2x-5=0
add 5 to both sides
2x=5
Divide by 2
x=5/2
2. (x+3)=0
subtract 3 from both sides
x=-3
Find all the local maxima, local minima, and saddle points of the function. 4xy-x^2-6y^2 5x 5
Answers
The function \(\(f(x, y) = 4xy - x^2 - 6y^2 + 5x + 5\)\) has a local maximum at \(\(\left(\frac{15}{2}, \frac{5}{2}\right)\)\).
To find the local maxima, local minima, and saddle points of the function \(\(f(x, y) = 4xy - x^2 - 6y^2 + 5x + 5\)\), we need to calculate its partial derivatives and analyze their critical points.
Step 1: Calculate the partial derivatives:
\(\(\frac{{\partial f}}{{\partial x}} = 4y - 2x + 5\)\)
\(\(\frac{{\partial f}}{{\partial y}} = 4x - 12y\)\)
Step 2: Set the partial derivatives equal to zero and solve for x and y to find the critical points:
For \(\(\frac{{\partial f}}{{\partial x}} = 0\)\):
4y - 2x + 5 = 0
For \(\(\frac{{\partial f}}{{\partial y}} = 0\)\):
4x - 12y = 0
Solving these two equations simultaneously, we get:
4y - 2x + 5 = 0
4x - 12y = 0
From the second equation, we have (x = 3y). Substituting this into the first equation:
\(\(4y - 2(3y) + 5 = 0\)\)
\(\(4y - 6y + 5 = 0\)\)
\(\(-2y + 5 = 0\)\)
\(\(2y = 5\)\)
\(\(y = \frac{5}{2}\)\)
Substituting the value of (y) back into (x = 3y):
\(\(x = 3 \left(\frac{5}{2}\right)\)\)
\(\(x = \frac{15}{2}\)\)
So, the critical point is \(\(\left(\frac{15}{2}, \frac{5}{2}\right)\)\).
Step 3: Analyze the critical points to determine if they are local maxima, local minima, or saddle points.
To classify the critical points, we need to calculate the second-order partial derivatives and evaluate the determinant and the discriminant of the Hessian matrix.
The Hessian matrix is given by:
\(\(H(x, y) = \begin{bmatrix} \frac{{\partial^2 f}}{{\partial x^2}} & \frac{{\partial^2 f}}{{\partial x \partial y}} \\ \frac{{\partial^2 f}}{{\partial y \partial x}} & \frac{{\partial^2 f}}{{\partial y^2}} \end{bmatrix}\)\)
Calculating the second-order partial derivatives:
\(\(\frac{{\partial^2 f}}{{\partial x^2}} = -2\)\)
\(\(\frac{{\partial^2 f}}{{\partial x \partial y}} = 4\)\)
\(\(\frac{{\partial^2 f}}{{\partial y \partial x}} = 4\)\)
\(\(\frac{{\partial^2 f}}{{\partial y^2}} = -12\)\)
Evaluating the Hessian matrix at the critical point \(\(\left(\frac{15}{2}, \frac{5}{2}\right)\)\):
\(\(H\left(\frac{15}{2}, \frac{5}{2}\right) = \begin{bmatrix} -2 & 4 \\ 4 & -12 \end{bmatrix}\)\)
The determinant of the Hessian matrix is:
\(\(\Delta = \frac{{\partial^2 f}}{{\partial x^2}} \cdot \frac{{\partial^2 f}}{{\partial y^2}} - \left(\frac{{\partial^2 f}}{{\partial x \partial y}}\right)^2 = (-2) \cdot (-12) - (4)^2 = 24 - 16 = 8\)\)
The discriminant of the Hessian matrix is:
\(\(D = \frac{{\partial^2 f}}{{\partial x^2}} = -2\)\)
Based on the determinant and discriminant, we can determine the nature of the critical point:
1. If \(\(\Delta > 0\)\) and \(\(D > 0\)\), then the critical point is a local minimum.
2. If \(\(\Delta > 0\)\) and \(\(D < 0\)\), then the critical point is a local maximum.
3. If \(\(\Delta < 0\)\), then the critical point is a saddle point.
4. If \(\(\Delta = 0\)\), further analysis is required (such as higher-order derivatives or other methods).
In this case, we have \(\(\Delta = 8\)\) and \(\(D = -2\)\).
Since \(\(\Delta > 0\)\) and \(\(D < 0\)\), we conclude that the critical point \(\(\left(\frac{15}{2}, \frac{5}{2}\right)\)\) is a local maximum.
Learn more about Hessian matrix on:
https://brainly.com/question/31379954
#SPJ11
Find the LCM (step by step!)
12r^3, 18r^2t, 24t^4
Answers
Answer:
72r^3t^4
Step-by-step explanation:
* and x = times tables btw
First you'll want to rewrite the equation:
12r^3
18r^2t
24t^4
Then factor the monomial, 12r^3=2*2*3*r*r*r
18r^2t
24t^4
Finding the lease common multiple of the expressions, write the product of all factors the greatest number of times they appear in factorization.
12r^3=2*2*3*r*r*r
18r^2t=2*3*3*r*r*t
24t^4=2*2*2*3*t*t*t*t
Your answer is
2 x 2 x 2 x 3 x 3 x r x r x r x t x t x t
simplify it and you get
72r^3t^4
If a fair die is rolled 3 times, what is the probability, to the nearest thousandth, of getting exactly 2 fives?
Answers
Answer:
The answer is .578 you just do 5/6 due to the fact that there are 6 sides on a die and 1 side is a 2 so if you don’t get a two there is 5 sides left so you do 5/6 to the power of 3 leaving you with .578 and some
Step-by-step explanation:
The probability of getting exactly 2 fives in 3 rolls of a fair die is approximately 0.0694.
What is Probability?It is a branch of mathematics that deals with the occurrence of a random event.
The probability of getting a five on a single roll of a fair die is 1/6. The probability of not getting a five on a single roll is 5/6.
To find the probability of getting exactly 2 fives in 3 rolls, we can use the binomial probability formula:
\(P(X = k) = ^nC_{k} p^k(1-p)^n^-^k\)
Where n is the number of trials, n= 3
k is the number of successes we want, k=2
p is the probability of success on a single trial (1/6)
Plugging in the values, we get:
\(P(X = 2) = ^3C_{2}.(1/6)^2(5/6)^(^3^-^2^)\)
= 3. (1/6)²(5/6)
= 0.0694
Therefore, the probability of getting exactly 2 fives in 3 rolls of a fair die is approximately 0.0694
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ3
La temperatura de un congelador bajó de 3 °C a −9 °C en 3 horas. Si la temperatura del congelador bajó en la misma cantidad de grados cada hora, ¿qué temperatura tenía el congelador al completarse la primera hora?
Answers
Usando proporciones, se encuentra que al final de la primera hora, el congelador tenía una temperatura de -1ºC.
Este problema se resuelve por proporciones. En 3 horas, la temperatura bajó 12ºC, puesto que \(3 - (-9) = 12\).La temperatura del congelador bajó en la misma cantidad de grados cada hora, o sea, en la primera hora, la cantidad que bajo es:
\(\frac{12}{3} = 4\)
4ºC bajo a 3ºC es:
\(3 - 4 = -1\)
O sea, al final de la primera hora, el congelador tenía una temperatura de -1ºC.
Un problema similar es dado en https://brainly.com/question/24617308
please help me asap

Answers
Answer:
that's the lowest term actually
Let be the linear transformation given by let be the basis of given by and let be the basis of given by find the coordinate matrix of relative to the ordered bases and.
Answers
The value of the coordinate matrix is \(\begin{bmatrix} 2&3 &0 \\ 2& 2 & 6\\ 0& 2 &4 \\0 & 0& 2\end{bmatrix}\)
To find the coordinate matrix LFE, we need to express the images of the basis vectors of E in terms of the basis vectors of F. Let's start with e₁(t) = 1, which is a constant polynomial of degree 0. Applying L to this polynomial gives us L(e₁(t)) = 5(0) + 3(0) + 2(1) + 2t(1) = 2 + 2t. We want to express this polynomial as a linear combination of the basis vectors of F, so we write:
2 + 2t = a₁f₁(t) + a₂f₂(t) + a₃f₃(t) + a₄f₄(t)
where a₁, a₂, a₃, and a₄ are unknown coefficients. We can substitute the definitions of the basis vectors of F to obtain:
2 + 2t = a₁ + a₂t + a₃t² + a₄t³.
This is a system of linear equations in the variables a₁, a₂, a₃, and a₄. We can solve this system to obtain the coefficients as follows:
a₁ = 2
a₂ = 2
a₃ = 0
a₄ = 0
Therefore, the coordinate vector of L(e₁(t)) with respect to the basis F is [2, 2, 0, 0]ᵀ. Similarly, we can find the coordinate vectors of L(e₂(t)) and L(e₃(t)):
L(e₂(t)) = 5(0) + 3(1) + 2t(1) + 2t² = 2t² + 2t + 3
⇒ [L(e₂(t))]ₘ = [3, 2, 2, 0]ᵀ
L(e₃(t)) = 5(2) + 3(2t) + 2t²(1) + 2t(t²) = 2t³ + 4t² + 6t
⇒ [L(e₃(t))]ₘ = [0, 6, 4, 2]ᵀ
Finally, we can arrange these coordinate vectors as columns of a matrix to obtain the coordinate matrix LFE:
LFE = \(\begin{bmatrix} 2&3 &0 \\ 2& 2 & 6\\ 0& 2 &4 \\0 & 0& 2\end{bmatrix}\)
This is a 4x3 matrix because the range space has dimension 4 and the domain space has dimension 3. Each column of the matrix represents the coordinates of the image of a basis vector of E in terms of the basis vectors of F.
To know more about matrix here
https://brainly.com/question/28180105
#SPJ4
Complete Question:
Let L: P2 → P3 be the linear transformation given by
L(p(t)) = 5p"(t) + 3p'(t) + 2p(t) + 2tp(t).
Let E = (e₁, e₂, e₃) be the basis of P2 given by e₁(t) = 1, e₂(t) = t, e₃(t) = t². and let F = (f₁, f₂, f₃, f₄) be the basis of P3 given by f₁(t) = 1, f₂(t) = t, f₃(t) = t² , f₄(t) =t³".
Find the coordinate matrix LFE of L relative to the ordered bases E and F.
line 1: y=-2x+4 and line 2: y=-2x the system has exactly on solution or infinite solution or no solutions.
Answers
The system of equation line 1: y=-2x+4 and line 2: y=-2x has no solution.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
A mathematical equation is a statement with two equal sides and an equal sign in between. An equation is, for instance, 4 + 6 = 10. Both 4 + 6 and 10 can be seen on the left and right sides of the equal sign, respectively.
We are given the system of equation as;
line 1: y=-2x+4
line 2: y=-2x
Here we can put x = 1
Then;
y= -2(1) + 4
y = -2 + 4
y = 2
-2x=-2x+4
x = 0
Therefore, we can see that the system of equation has no solution.
Learn more about equations here;
https://brainly.com/question/25180086
#SPJ1
Work out m and c for the line: y = 6 − x
Answers
Put this into slope intercept form.
y = 6 - x becomes y = -x + 6
"m" is the coefficient on x: -1
"c" is the number without the x: 6
Answer:
m = 1
c = -6
Step-by-step explanation:
As y = mx + c (standard form)
Eli earned $64 at his job when he worked for 8 hours. Fill out a table of equivalent ratios and plot the points on the coordinate axes provided.
Whats the answer?
Answers
The table of equivalent ratios is added below
How to determine the equivalent ratiosTo fill out a table of equivalent ratios, we can start by finding the ratio of dollars earned to hours worked:
$64 / 8 hours = $8/hour
We can then use this ratio to find other equivalent ratios by multiplying or dividing both the numerator and denominator by the same number. For example:
$16 / 2 hours = $8/hour$24 / 3 hours = $8/hour$32 / 4 hours = $8/hour$40 / 5 hours = $8/hour$48 / 6 hours = $8/hour$56 / 7 hours = $8/hourHere is the completed table of equivalent ratios:
Dollars earned Hours worked
$8 1
$16 2
$24 3
$32 4
$40 5
$48 6
$56 7
$64 8
See attachment for the graph
Read more about equivalent ratios at
https://brainly.com/question/2328454
#SPJ1

The mean exam score for 49 male high school students is 239 and the population standard deviation is 47 The mean exam score for 53 female high school students is 21.1 and the population standard deviation is 4.3. At α=001, can you reject the claim that male and female high school students ha equal exam scores? Complete parts (a) through (e). Click here to view page 1 of the standard normal distribution table. Click here to view. page 2 of the standard normal distribution table. A. Male high school students have lower exam scores than female students B. Male and temale high school students have different exam scores. C. Male and female high school students have equal exam scores D. Male high school students have greater exam scores than female students
Answers
Comparing the means of the two samples, we find that the difference between the means is significant. Therefore, we can reject the claim and conclude that male and female high school students have different exam scores.
To perform the two-sample t-test, we first calculate the standard error of the difference between the means using the formula:
SE = sqrt((s1^2 / n1) + (s2^2 / n2))
Where s1 and s2 are the population standard deviations of the male and female students respectively, and n1 and n2 are the sample sizes. Plugging in the values, we have:
SE = sqrt((47^2 / 49) + (4.3^2 / 53))
Next, we calculate the t-statistic using the formula:
t = (x1 - x2) / SE
Where x1 and x2 are the sample means. Plugging in the values, we have:
t = (239 - 21.1) / SE
We can then compare the t-value to the critical t-value at α = 0.01 with degrees of freedom equal to the sum of the sample sizes minus 2. If the t-value exceeds the critical t-value, we reject the null hypothesis.
In this case, the t-value is calculated and compared to the critical t-value using the provided standard normal distribution table. Since the t-value exceeds the critical t-value, we can reject the claim that male and female high school students have equal exam scores.
Therefore, the correct answer is:
B. Male and female high school students have different exam scores.
Learn more about hypothesis testing here: brainly.com/question/17099835
#SPJ11
if you use 1 pound of mirepoix in a recipe that yields 1 gallon of soup, how much mirepoix do you need to make 31/2 gallons of soup?
Answers
we need 31/2 pounds mirepoix to make 31/2 gallons of soup.
let we need x% (percent) of mirepoix to make 1 gallon of soup
given we have 1 pound of mirpoix which yeilds 1 gallon soup of soup
so total amount of mirepoix that required in the solution is = \(\frac{x}{100} *1 pound\)
so x/100 = 1 gallon / pound
we will use this equation for further calculation
let we need y pounds of mirepoix to make 31/2 gallon of soup ans we know that x% of mirepoix is required for this solution.
so \(\frac{x}{100} * y = 31/2\)
ans in the above equation x/100 =1 gallon / pound
so 1 * y= 31 /2
and hence y = 31/2 pounds
so we need 31/2 pounds of mirepoix to form requied amount of soup.
To know more about percent click on below link:
https://brainly.com/question/29200507?referrer=searchResults
#SPJ4
Evaluate the following
a) 5 ÷ 2 (mod 6)
b) 9 ÷ 7 (mod 7)
c) 3 × 2 ÷ 5 (mod 7)
Answers
Neither 2 nor 7 have inverses mod 6 or 7, respectively, so the expressions in (a) and (b) cannot really evaluated... At least we can evaluate (c) :
\(5\times3 \equiv 15 \equiv 1 \pmod 7 \\\\ \implies 3\times2\div5 \equiv 3\times2\times3 \equiv18 \equiv \boxed{4 \pmod{7}}\)
One brand of juice contains 0.05 of natural juice. Which is this decimal written as a percent?
A) 0.05%
B) 5%
C) 0.5%
D) 50%
Answers
Answer:
B.) 5%
Step-by-step explanation:
You'll need to multiply 0.05 by 100. Since 100 = 1, we are only multiplying by 1 and not changing the value of our number.
0.05 × 100 = 5
5/100 is 5 over 100 and means 5 per 100. 5 "per 100" means 5 "percent" or 5%
Therefore, 0.05 = 5%
I hope this helps! ^-^
0.05 x 100 = 5
What is a function in math?
if you explain I will make you brainiest!
Answers
Answer:
A function is an equation in math that connects an input to a given output.
Step-by-step explanation:
Help pleasee!!! THANK YOUUU

Answers
Answer: 5 , 5, 2, $40, $10
Step-by-step explanation:
He gets paid $10 a week minus the $2 he donates so he will have $8 times five weeks left for a total of $40
Multiply the polynomials. Express the answer as single polynomial in standard form. (6x - 7)²
Answers
the product of the polynomial (6x - 7)² is 36x² - 84x + 49, expressed in standard form.
To multiply the polynomial (6x - 7)², we can use the concept of binomial expansion or the FOIL method. Let's apply the FOIL method:
(6x - 7)² = (6x - 7)(6x - 7)
Using the FOIL method, we multiply the first terms, outer terms, inner terms, and last terms:
(6x - 7)(6x - 7) = 6x * 6x + 6x * (-7) + (-7) * 6x + (-7) * (-7)
Simplifying each term:
= 36x² - 42x - 42x + 49
= 36x² - 84x + 49
Therefore, the product of the polynomial (6x - 7)² is 36x² - 84x + 49, expressed in standard form.
Learn more about polynomial here
https://brainly.com/question/11536910
#SPJ4
What is the answer to this problem?
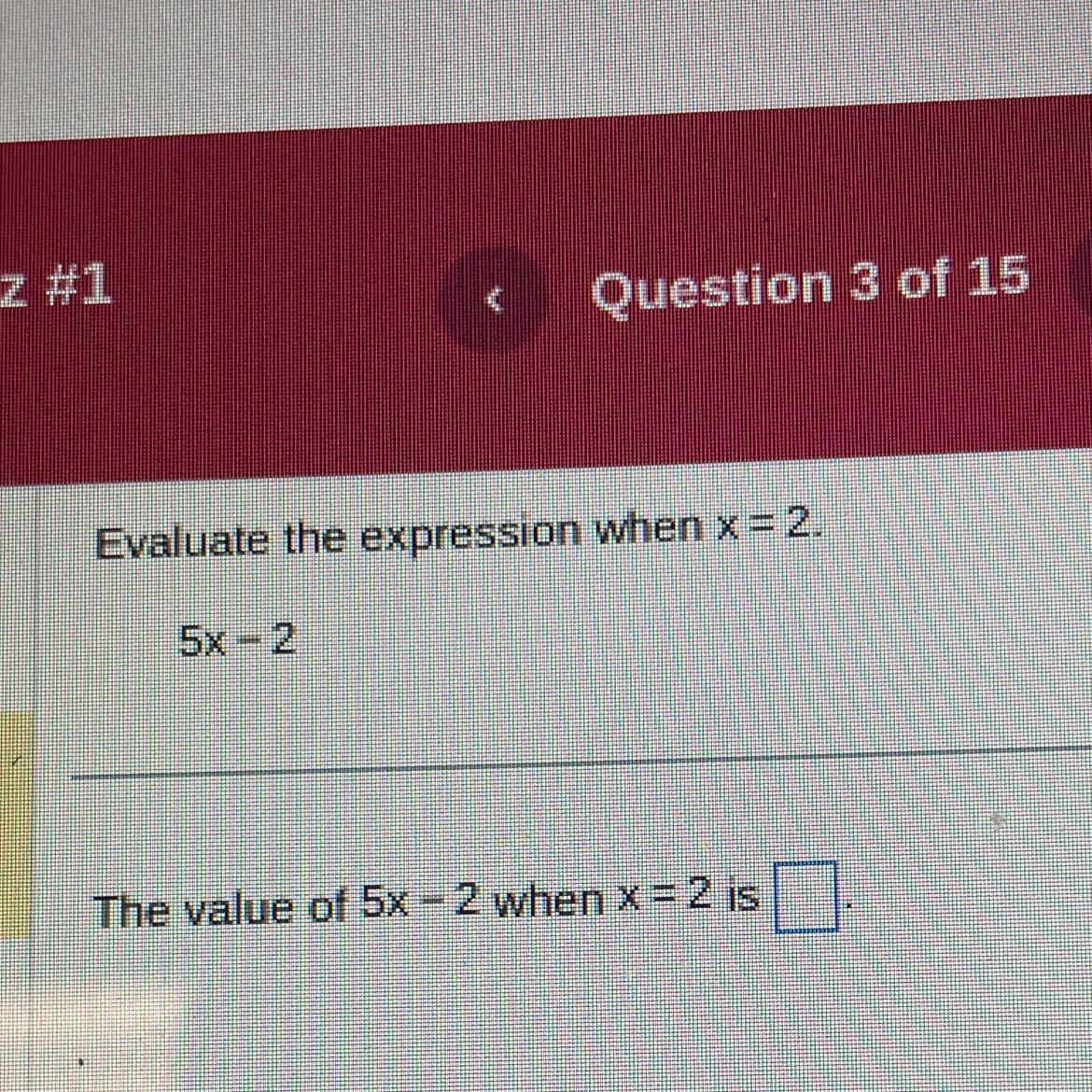
Answers
Answer:
8
Step-by-step explanation:
Given: x=2
Then,
5x-2 = 5(2)-2
= 10-2
=8
A square has a side length x and a circle has a radius (x-1). At what value of x will the two figures have the same area?
a. 1.66
b. 2.29
c. 0.5
d. 1.25
Answers
Answer:
B
Step-by-step explanation:
The area of the square can be calculated using S^2 = x^2
The area of the circle is pi * r^2
= 22/7 * (x-1)^2
= 22(x-1)^2/7
So we need the value of x, that will make;
x^2 = 22(x-1)^2/7
In this kind of scenario, since we have options, it is best to test values instead of going through long calculations
Let’s try 2.29
So;
2.29^2 = 22/7(2.29-1)^2
5.2441 = 5.23
So close , but let’s see if any other value will
give us a closer value
Let’s work with 1.66
1.66^2 = 22/7(1.66-1)^2
2.7556 = 1.369
This is far from what we need
Let’s try 0.5
0.5^2 = 22/7(0.5-1)^2
Thus gives a negative answer on the right hand side, so no need trying
And lastly 1.25
1.25^2 = 22/7(1.25-1)^2
1.5625 = 0.1946
So the first test still gives the most probable answer to a decimal place accuracy
Answer:
b. 2.29
Step-by-step explanation:
the answer above is correct please give them the brainiest
How to find a circle given its diameter
Answers
Answer:
To find a circle given its diameter, you can use the following formula:
C = πd
where C is the circumference of the circle, d is the diameter, and π (pi) is a mathematical constant approximately equal to 3.14.
If you want to find the area of the circle, you can use the following formula:
A = πr²
where A is the area of the circle, and r is the radius (which is half the diameter).
Answer:
area of circle or round of it?
i don’t understand how to do these and this assignment is due today :((

Answers
Answer:
Step-by-step explanation:
8 , 12 , 16 , 20 .......
First term = a = 8
Common difference = second term - first term = 12 - 8= 4
nth term = a + (n-1) * d
= 8 + (n -1) * 4
= 8 + 4n - 4
= 4n + 8 - 4
= 4n + 4