For the function y = 5 – 4x, given the domain {-1, 0, 1}, the range is
Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
{1, 5, 9}
»»————- ★ ————-««
Here’s why:
⸻⸻⸻⸻
\(y = 5 - 4x\\\\\rightarrow y = 5-4(-1)\\\\\rightarrow y = 5 + 4\\\\\rightarrow \boxed{y = 9}\)
⸻⸻⸻⸻
\(\rightarrow y = 5 - 4(0)\\\\\rightarrow y = 5 - 0\\\\\rightarrow \boxed{y = 5}\)
⸻⸻⸻⸻
\(\rightarrow y = 5 - 4(1)\\\\\rightarrow y = 5 - 4\\\\\rightarrow \boxed{y = 1}\)
⸻⸻⸻⸻
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
Related Questions
Jodi is going to start up a cookie baking business over the summer to make some extra money. It costs her $2.45 in supplies to make a dozen cookies. She wants to markup the price by 150%. How much should she sell a dozen cookies for? $
Answers
will give brainliest to quickest answer

Answers
Answer:
The vertex is option C: (-6, -2)
Step-by-step explanation:
The equation for a parabola is y = a(x – h)² + k where h and k are the y and x coordinates of the vertex, respectively. Thus, the vertex is (-6,2)
Pls mark brainliest.
Which is NOT a proposition
A. Marlon is eating his lunch
B. Will you be at school tomorrow.
C. The earth is rectangular
D. 10 + 5 = 15
Answers
Answer:the answer is b
Step-by-step explanation:reason being that the question will you be at school tmrw?cat be given a choice to say wether it’s true or false so Yh...I don’t know if that helped
Please look at photo and ignore already selected answer

Answers
Answer:
Question (A) firgue b is pallorgram
Question ( B) Only A is a rentengle
Question (C) is already right
Step-by-step explanation:
B. Shape A
C. Shape C
Mark as brainliest plz
Find the change in profit P for the given marginal. Assume that the number of units x increases by 5 from the specified value of x. (Round your answer to two decimal places.) Marginal Number of Units, x dP dx = 12.1 60 − 3 x x = 121
Answers
The change in profit (ΔP) when the number of units (Δx) increases by 5, based on the given marginal profit function, is -18331.50
To find the change in profit (ΔP) when the number of units (Δx) increases by 5.
we need to evaluate the marginal profit function and multiply it by Δx.
The marginal profit function is given by dP/dx = 12.1(60 - 3x).
We are given the value of x as 121, so we can substitute it into the marginal profit function to find the marginal profit at that point.
dP/dx = 12.1(60 - 3(121))
= 12.1(60 - 363)
= 12.1(-303)
= -3666.3
Now, we can calculate the change in profit (ΔP) by multiplying the marginal profit by Δx, which is 5 in this case.
ΔP = dP/dx×Δx
= -3666.3 × 5
= -18331.5
To learn more on Change in Profit click:
https://brainly.com/question/31420071
#SPJ4
The sides of a rectangle measure 14 and 21. The perimeter of a similar rectangle is 40. What are the lengths of its Sides
Answers
Answer:
8 and 12
Step-by-step explanation:
The perimeter of the given rectangle is ...
P = 2(L +W)
P = 2(14 +21) = 2(35) = 70
The scale factor to the similar triangle is ...
similar perimeter/original perimeter = 40/70 = 4/7
__
The dimensions of the similar triangle are the original triangle dimensions multiplied by this scale factor:
(14)(4/7) = 8
(21)(4/7) = 12
The sides of the similar triangle are 8 and 12.
The seventh-grade band is going to sell baked goods at the craft show. The cost to rent a booth at the craft show is $60. The band plans to charge $1.50 per baked good.
How many baked goods must they sell in order to profit at least $200?
A. 93 baked goods
B. 94 baked goods
C. 173 baked goods
D. 174 baked goods
Answers
first they need to cover the cost of the booth, 60$
to do that they would need to sell
60/1.5= 40 baked goods
then earn 200$
200/1.5=133.3333....
you cant sell part of the baked good so you would need to round up to 134
134+40= 174 baked goods
my
test, please help :/
9. [-15 Points) DETAILS LARCALCET7 5.7.042. MY NOTES ASK YOUR TEACHER Find the indefinite integral. (Remember to use absolute values where appropriate. Use for the constant of integration.) I see sec
Answers
The indefinite integral of sec(x) is (1/2) ln|(1 + tan(x/2))/(1 - tan(x/2))| + C, where C is the constant of integration.
To find the indefinite integral of sec(x), we can use a technique called substitution.
Let u = tan(x/2), then we have: sec(x) = 1/cos(x) = 1/(1 - sin^2(x/2)) = 1/(1 - u^2). Also, dx = 2/(1 + u^2) du. Substituting these into the integral, we get: ∫sec(x) dx = ∫(1/(1 - u^2))(2/(1 + u^2)) du. Using partial fractions, we can write: 1/(1 - u^2) = (1/2)*[(1/(1 - u)) - (1/(1 + u))]
Substituting this into the integral, we get: ∫sec(x) dx = ∫[(1/2)((1/(1 - u)) - (1/(1 + u))))(2/(1 + u^2))] du. Simplifying this expression, we get: ∫sec(x) dx = (1/2)∫[(1/(1 - u))(2/(1 + u^2)) - (1/(1 + u))(2/(1 + u^2))] du
Using the natural logarithm identity ln|a/b| = ln|a| - ln|b|, we can simplify further: ∫sec(x) dx = (1/2) ln|(1 + u)/(1 - u)| + C. Substituting back u = tan(x/2), we get: ∫sec(x) dx = (1/2) ln|(1 + tan(x/2))/(1 - tan(x/2))| + C. Therefore, the indefinite integral of sec(x) is (1/2) ln|(1 + tan(x/2))/(1 - tan(x/2))| + C.
to know more about natural logarithm, click: brainly.com/question/29154694
#SPJ11
The table shows a students results from spinning the pointer 30 times. Find the experimental probability that the pointer lands in a section with a number greater than or equal to 3.

Answers
Answer:
The answer is 8/15
hope it helps you
HELPPPP I NEED THIS QUICKLY!!

Answers
A) Yes it is a function and f(x)=2.80+3.50x so 2.80 is an independent function and 3.50x is dependent function
B) Domain x = (0,20] and Range y = (2.8,72.8]
A dependent function is what?
A dependent function type is one whose outcome depends on the parameters of the function.
Independent function: What is it?
Independent function (plural independent functions) as a noun (mathematics) any one of a group of functions whose value cannot be inferred from the values of all the others.
Given: The expression y = 3.5x + 2.8 calculates the y (in dollars) cost of an x-mile taxi fare. You have enough cash to take a cab for a maximum of 20 kilometres.
Domain and range to find
Solution:
y = 3.5x + 2.8
cost y (in dollars)
miles, in.
You have enough cash to take a cab for a maximum of 20 kilometres.
0 < x ≤ 20
Therefore, x = [0, 20].
Domain x = [0, 20]
y = 3.5x + 2.8
x = 0
=> y = 0 + 2.8 = 2.8
x = 20
=> y = 3.5(20) + 2.8
=> y = 70 + 2.8
=> y = 72.8
2.8 < y ≤ 72.8
y = (2.8 , 72.8 ]
Range = (2.8 , 72.8 ]
Learn More :
Find the domain and range of the function f(x)= √9-x² . OR. Let f ...
brainly.in/question/24822483
Consider this function. f(x) = |x – 4| + 6 If the domain is restricted to
brainly.in/question/23841328
#SPJ13
The ratio of dogs to all pets in a pet store was 2:3. If there were 21 total pets in the pet store, how many were dogs?
Answers
Answer:
Step-by-step explanation:
14
Answer:
14 will be your answer for that question
Help please!
What is the probability of picking a purple marble and spinning green? 2 Answer: Write the answer as a simplified fraction.
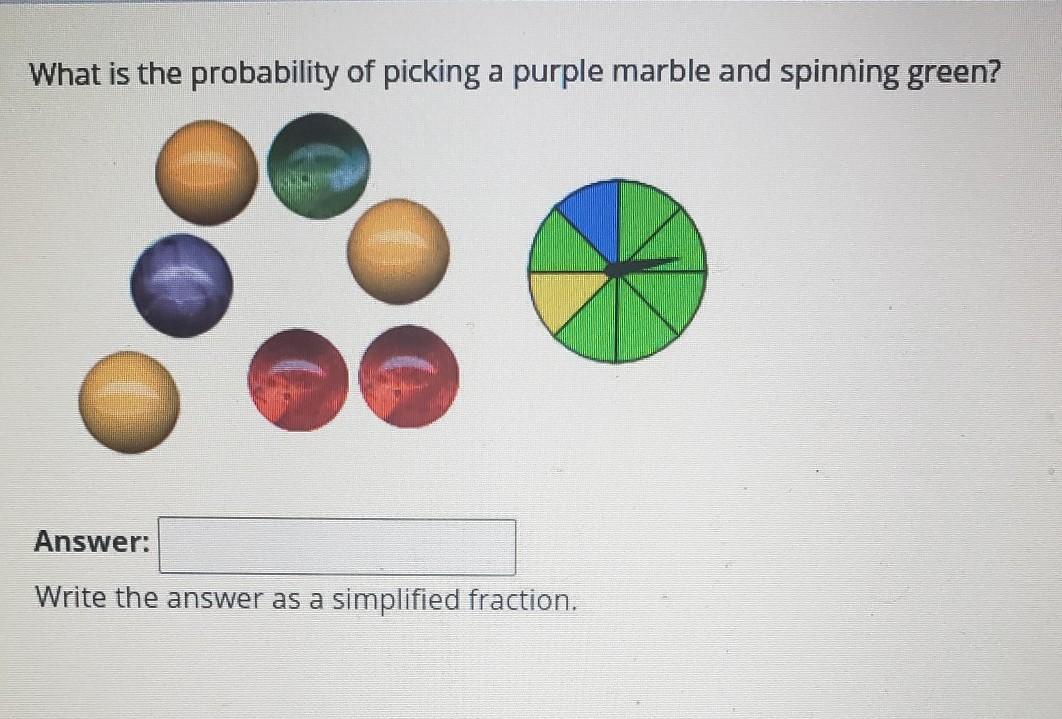
Answers
Answer:
3/28
Step-by-step explanation:
1/7 times 6/8
A rhombus has sides of length 6cm. One of its diagonals is 10cm long. Find the length of the other diagonal
Answers
Answer: The length of the other diagonal is approximately 5.83 cm (rounded to two decimal places).
Step-by-step explanation:
Label the diagonals of the rhombus as d1 and d2. Since the diagonals of a rhombus intersect at a 90-degree angle, we can use the Pythagorean theorem to relate the diagonals and the side length:
d1^2 = (6/2)^2 + (d2/2)^2
d1^2 = 9 + (d2/2)^2
We also know that the length of one diagonal is 10cm:
d2 = 10
We can substitute this value into the equation for d1:
d1^2 = 9 + (10/2)^2
d1^2 = 9 + 25
d1^2 = 34
Taking the square root of both sides, we get:
d1 = sqrt(34)
I need to know what to fill out

Answers
The function is a linear function because as x increases, the y-value changes at a constant rate . The rate of change of this equation is 2.
How to find linear functions?The difference between linear and exponential functions is that Linear functions change at a constant rate per unit interval while an exponential function changes by a common ratio over equal intervals.
We are given the function table as:
(0, -3)
(1, -1)
(2, 1)
(3, 3)
Thus, we can see that as x increases, the y-value changes at a constant rate of + 2.
Read more about Linear Functions at: https://brainly.com/question/15602982
#SPJ1
Need someone to help my on my homework will do ANYTHING please help but pls have an app to text so we can work on it it is mathematics.
Answers
Answer:
i willl maybe help but
Step-by-step explanation:
Describe the process as civilizations in Africa changed from Hunter and Gatherer communities to civilizations.
A system of equations consisting of a linear equation and a quadratic equation has infinitely many solutions. Is this statement true?.
Answers
A system of equations consisting of a linear equation and a quadratic equation has infinitely many solutions is not true.
Linear equations are equations that graph as a line, while the quadratic equations are that graph as a parabola. Lines and parabolas in the xy-plane are convenient representations of linear and quadratic systems, respectively. One solution to the system is shown by each point where the line and parabola intersect. It is possible for a line and a parabola to intersect zero, one, or two times. This indicates that a linear and quadratic system may have zero, one, or two solutions.
To learn more about linear equation and quadratic equation, click here:
https://brainly.com/question/29550670
#SPJ4
What is the difference quotient for the function f (x) = negative startfraction 1 over 5 x minus 12 endfraction?
Answers
The difference quotient of f(x) is \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\) .
According to the given question.
We have a function
f(x) = -1/(5x -12)
As we know that, the difference quotient is a measure of the average rate of change of the function over and interval.
The difference quotient formula of the function y = f(x) is
[f(x + h) - f(x)]/h
Where,
f(x + h) is obtained by replacing x by x + h in f(x)
f(x) is a actual function.
Therefore, the difference quotient formual for the given function f(x)
= [f(x + h) - f(x)]/h
= \(\frac{\frac{-1}{5(x+h)-12} -\frac{-1}{5x-12} }{h}\)
= \(\frac{\frac{-1}{5x + 5h -12}+\frac{1}{5x-12} }{h}\)
= \(\frac{\frac{-1+5h}{5x + 5h-12} }{h}\)
= \(\frac{-1+5h}{(5x +h-12)(h)}\)
= \(\frac{-1+5h}{5xh + h^{2} -12h}\)
= \(\frac{h(-\frac{1}{h}+5) }{h(5x+h-12)}\)
= \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\)
Hence, the difference quotient of f(x) is \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\) .
Find out more information about difference quotient here:
https://brainly.com/question/18270597
#SPJ4
find : a 1/2 of i 2 3/4 ii 4 2/9
Answers
1) 2 3÷4 = 11÷4
hence, 11÷8 = 1.37 .
2) 4 2÷9 =38÷9 .
hence, 38÷18 = 2.11 .
simplify 2 3÷4 = 11÷4
and
4 2÷9 = 38÷9.
now 1/2 of 11/4 = 11/8 = 1.37.
1/2 of 38/9 = 38/18 = 2.11 .
4x-3y=6
4x+y=14 type a ordered pair
Answers
Answer:
(3,2)
Step-by-step explanation:
If you graph the equations, they cross at this point.
Using proportional reasonings make a prediction about how many students you would expect to have plans to attend college
Answers
The National Center for Education Statistics estimates that 69% of high school graduates in the US plan to attend college after graduation, but this is only an estimate based on general trends and assumptions. The actual proportion of college-bound students in a given population may differ depending on socioeconomic status, location, and individual interests and goals.
In a town with 20,000 residents, 30% are high school students. If 70% of high school students plan to attend college, how many students would you predict will attend college?Assuming that the percentage of high school students who plan to attend college in the town is representative of the national average, we can use proportional reasoning to make a prediction about the number of students who would attend college.
Out of 20,000 residents, 30% or 6,000 are high school students. If 70% of these students plan to attend college, we can calculate the number of students who will attend college as follows:
6,000 x 0.70 = 4,200
Therefore, based on the given data, we can predict that around 4,200 students in the town will attend college. However, this is just an estimation, and other factors such as economic conditions and the availability of colleges and universities may affect the actual number of students who attend college.
To know more about Socioeconomic visit:
https://brainly.com/question/7291812
#SPJ1
Substititue 5 for x. Is the solution true?
3x + 4 - x = 4x - 6
Answers
Answer:
It's a true solution.
Step-by-step explanation:
\(3(5) + 4 - 5 = 4(5) - 6\)
\(15 + 4 - 5 = 20 - 6\)
\(19 - 5 = 14\)
\(14 = 14\)
what is 21000 take away two thirds
Answers
Answer:
7000
Step-by-step explanation:
21000/0.667
=14000
21000-14000
=7000
Michelle plans to install new laminate flooring. Each case of the flooring will cover 19. 63 square feet. How many cases of flooring will michelle need to buy to install new flooring in the office floor and living room floor?.
Answers
Number of cases of flooring Michelle needed to buy to install new flooring in the office floor and living room floor can be found by the equation x = (A₁ + A₂) / 19.63 where A₁ and A₂ are the area of the office floor and living room floor respectively.
What is Multiplication?Multiplication is a basic operation in mathematics where when two numbers are multiplied, one number is actually repeated to that times as that of the other number and vice versa.
In other words, a × b implies that a is added repeatedly up to b times or b is added repeatedly up to a times.
Let the area of the office floor be A₁.
Let area of the living room floor be A₂.
Then the total area Michelle needs to do the flooring will be A₁ + A₂.
Area covered by 1 case of flooring = 19.63 square feet
Let x be the number of cases which cover the total area.
Then 19.63x will be the total area A₁ + A₂.
19.63x = A₁ + A₂.
Or x = (A₁ + A₂) / 19.63
Hence, if the area of the office floor and living room floor are given, we can find the number of cases needed to do the total flooring by the equation x = (A₁ + A₂) / 19.63.
To learn more about Multiplication, click:
https://brainly.com/question/11527721
#SPJ1
Find an ordered triple that represents 65 = (2, 6, 8) and Ž = (1, -2, 6).

Answers
Answer:
< 40, 28, 72 >
Step-by-step explanation:
Given
y = < 2, 6, 8 > and z = < 7, - 2, 6 > , then
6y + 4z
= 6 < 2, 6, 8 > + 4 < 7, - 2, 6 >
Multiply each component by the scalar quantity
= < 6(2), 6(6), 6(8) > + < 4(7), 4(- 2), 4(6) >
= < 12, 36, 48 > + < 28, - 8, 24 >
Add corresponding components
= < 12 + 28, 36 - 8, 48 + 24 >
= < 40, 28, 72 >
how to prove that lines that have a product of -1 is perpendibular
Answers
To prove that lines with a product of -1 are perpendicular, we can use the concept of slopes. If the product of the slopes of two lines is -1, then the lines are perpendicular to each other.
Let's consider two lines, L₁ and L₂, with slopes m₁ and m₂, respectively. The condition for perpendicularity states that m₁ * m₂ = -1.
To understand why this condition holds true, we can examine the geometric interpretation. The slope of a line represents the tangent of the angle between the line and the x-axis. When two lines are perpendicular, their angles between them are 90 degrees, or π/2 radians. The tangent of π/2 is undefined.
If m₁ * m₂ = -1, then either m₁ or m₂ must be the reciprocal of the other. This implies that one line has a positive slope, while the other has a negative reciprocal slope. The positive and negative slopes result in lines that are perpendicular to each other, forming a right angle at their intersection.
Therefore, when the product of the slopes of two lines is -1, the lines are proven to be perpendicular.
To learn more about slopes: -brainly.com/question/3605446
#SPJ11
Explain it too and what specific polynomial subject.

Answers
Answer:
C
Step-by-step explanation:
Expand the factors and compare the coefficients of like terms.
Given
(mx + 2)(3x - 5) ← expand using FOIL
= 3mx² - 5mx + 6x - 10
Compare to 12x² - 14x - 10
For the 2 to be equal, then the coefficients of like terms must be equal.
Compare coefficients of x² terms
3m = 12 ( divide both sides by 3 )
m = 4 → C
72 POINTS PLEASE HELP ME OR I WILL GET IN TROUBLE
Solve the following equation by showing all steps.
3 ( x – 2 ) = 15
Start by using distributive property:
Answers
Answer:
x=7
Step-by-step explanation:
distributive property: multiply both terms in the parentheses by the term outside the parentheses (3)
3 times x = 3x
3 times -2= -6
3x-6=15
move -6 to other side by adding 6+15
3x=21
divide 21 by 3
x=7
Answer:
x=7
Step-by-step explanation:
Evalute to 3x-6=15, then add 6 to both sides. Then, divide 3 by both sides to get x by itself getting you a answer which becomes, x=7.
The z score associated with the highest 10% is closest to
a. .0398
b. .5398
c. 1.28
d. -1.28
Answers
The z score associated with the highest 10% is closest to: option (c) 1.28
-To find the z score associated with the highest 10%, first determine the percentage that corresponds to the lower 90%, since the z score table typically represents the area to the left of the z score.
- Look up the 0.90 (90%) in a standard normal distribution (z score) table, which will give you the corresponding z score.
-The z score closest to 0.90 in the table is 1.28, which corresponds to the highest 10% of values.
Therefore, the z score associated with the highest 10% is closest to 1.28.
To know more about "standard normal distribution" refer here:
https://brainly.com/question/29509087#
#SPJ11
Please hurry 12 people fit comfortably in a 5 by 5 feet area. Use this value to estimate the size of a crowd that is 10 feet deep on ONE side of the street along a 1 mile section of a parade route. 25344 people 25344 people 52800 people 52800 people 110000 people 110000 people 20 people 20 people
Answers
hope this helps! Its the answer key to something almost exact
The size of the crowd that is 10 feet deep on ONE side of the street along a 1-mile section of a parade route is 25344 option (A) 25344 is correct.
What is a fraction?Fraction number consists of two parts, one is the top of the fraction number which is called the numerator and the second is the bottom of the fraction number which is called the denominator.
It is given that:
12 people fit comfortably in a 5 by 5 feet area.
Let x be the size of a crowd that is 10 feet deep on ONE side of the street along a 1-mile section of a parade route.
The fractions:
12/25 = x/(5280×10)
After cross multiplication:
25x = 633600
x = 633600/25
x = 25344
Thus, the size of the crowd that is 10 feet deep on ONE side of the street along a 1-mile section of a parade route is 25344 option (A) 25344 is correct.
Learn more about the fraction here:
brainly.com/question/1301963
#SPJ2
The formula below gives the sum of the degrees, S, of the interior angles of a polygon. If n represents the number of sides, which equation solves for n?
S = (n-2) x 180
F. n = s/180 + 2
G. n = 180s + 2
H. n = s+2/180
J. n = (s+2) x 180
Answers
Answer: F. n = s/180 + 2
Step-by-step explanation:
To find the equation that solves for n, we will isolate the n variable.
Given:
S = (n - 2) x 180
Divide both sides of the equation by 180:
\(\frac{S}{180}\) = n - 2
Add 2 to both sides of the equation:
\(\frac{S}{180}\) + 2 = n
Reflexive property:
n = \(\frac{S}{180}\) + 2
F. n = s/180 + 2