find the three consecutive odd integers such that the sum of twice the first and three times the second is 67 more than twice the thirdz
Answers
Answer:
23, 25, 27
Step-by-step explanation:
It can be convenient to work "consecutive integer" problems by using a variable to represent the middle one.
__
setupLet x represent the middle integer. Then (x-2) is the first of the three odd integers, and (x+2) is the third. The given relation is ...
2(x -2) +3x = 67 +2(x +2)
solution5x -4 = 2x +71 . . . . . simplify
3x = 75 . . . . . . . . add 4-2x
x = 25 . . . . . . . divide by 3
The three integers are 23, 25, 27.
Related Questions
Cones A and B both have volume 48bold pi cubic units, but have different dimensions. Cone A has radius 6 units and height 4 units. Find one possible radius and height for Cone B. Explain how you know Cone B has the same volume as Cone A.
Answers
Cone B does not have volume 48bold pi cubic units with these dimensions, but it does have the same volume as Cone A because they both have volume 48bold pi cubic units.
what is a cone?A cone, also known as a vertex, is a three-dimensional polygonal object with a flat base and a soft tapering apex. In a plane with no vertices, a cone is formed by connecting a story arc of lines, half-lines, but rather routes those are common to all focuses on the outpost. A cone is a muti structure with just a peaceful transition from a flat, round or, base towards the vertex and apex, which represents as the base's axis. A three-dimensional polygonal shape with only an upwardly flat curved surface is known as a cone.
Because Cone A has a volume of 48bold pi cubic units, we can use the volume of a cone formula to calculate its height:
Cone volume = 1/3 * base area * height
1/3 * pi * 62 * 4 = 48bold pi
48pi = 48bold pi
As a result, Cone A's height is 4 units. The radius is also 6 units, as we can see.
Cone volume = 1/3 * base area * height
\(1/3 * pi * r2 * h = 48\\144 = r^2 * h\\144 = 8^2 * 3\\144 = 192\)
Cone B does not have volume 48bold pi cubic units with these dimensions, but it does have the same volume as Cone A because they both have volume 48bold pi cubic units.
To know more about cone visit:
https://brainly.com/question/16394302
#SPJ1
Evaluate 5.48 x 2.45 (Answer to 2 decimal places). (a) 134.26 (b) 144.26 (c) 13.43 (d) 13.42 (e) 12.426
Answers
The final value is 13.43, which represents the product of 5.48 and 2.45.
We have,
The concept being demonstrated here is the multiplication of two decimal numbers.
When multiplying decimal numbers, we follow these steps:
- Ignore the decimal points and multiply the numbers as if they were whole numbers.
In this case, we multiply 548 by 245, which gives us 134,260.
- Determine the total number of decimal places in the original numbers.
In this case, the original numbers have a total of four decimal places (two decimal places each).
- Place the decimal point in the product so that it has the same number of decimal places as the total from step 2.
In this case, we need to place the decimal point two places from the right, giving us 1,342.60.
- Round the final result if necessary.
In this case, rounding to two decimal places gives us 1,342.60 rounded to 13.43.
Therefore,
The final value is 13.43, which represents the product of 5.48 and 2.45.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Use the menu provided to answer the following question. If a student purchased 1 can of juice, 2 slices of pizza, 1 bag of peanuts, and two chocolate bars using a $20.00 bill, what was her change?

Answers
Answer:
$8.25
Step-by-step explanation:
1.25+(2.25x2)+1.00+(1.25x2)=8.25
Mrs. Aldridge spilled coffee on her Answer Key and can't see the width of
the rectangle anymore. What would be the width of a rectangle with the
given area (shown in image below)?
x +9
x² + 11x + 18
(My answer is a guess so please show your work if you answer this question!)
thank you:)

Answers
Answer:
x + 2
Step-by-step explanation:
Area = x² + 11x + 18
length = x + 9
width = ?
Area = length x width
Factor the polynomial x² + 11x + 18:
length x width = (x + 9)(x + 2) = x² + 11x + 18
The length is x + 9, therefore the width is x + 2
Need help with this

Answers
Answer:
It's B. n3 - 4n - 4
Step-by-step explanation:
Hope this helps.. ;)
Helppppppppppppppppp
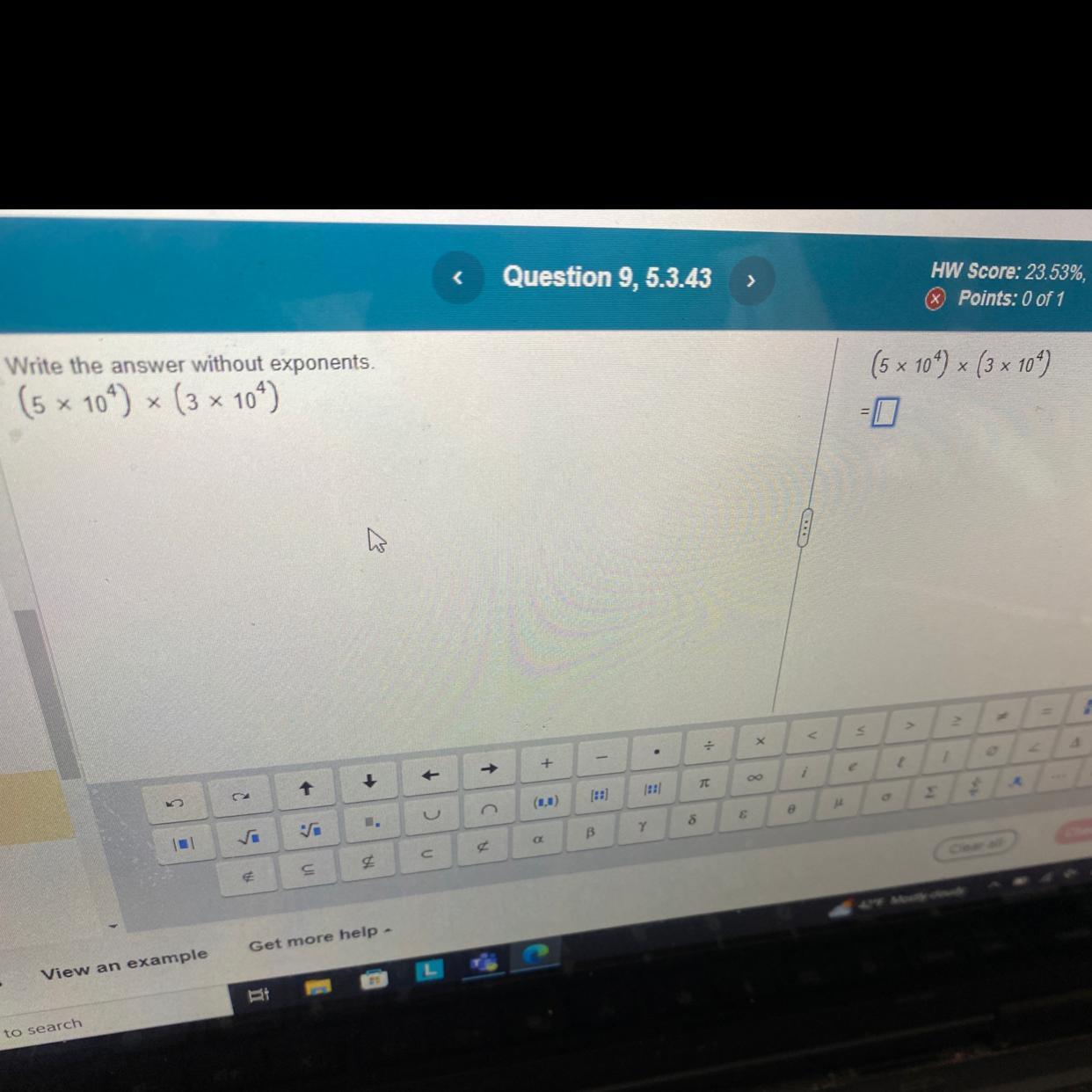
Answers
Find a polynomial function of degree 2 that has zeros at x=4

Answers
Hello there. To solve this question, we'll have to remember some properties about polynomial functions.
We have to find which option contains a polynomial function of degree 2 that has two zeros at x = 4.
Since all the options are degree 2 polynomials, this means that we want to determine a polynomial function that has discriminant zero, since its two roots are equal.
We can determine the discriminant for the equation:
\(ax^2+bx+c=0,a\ne0\)with the following formula:
\(\Delta=b^2-4ac\)Plugging in the values for each of the options, we get, in the same order:
\(\begin{gathered} \Delta_1=8^2-4\cdot1\cdot16=64-64=0 \\ \Delta_2=(-8)^2-4\cdot1\cdot16=64-64=0 \\ \Delta_3=3^2-4\cdot1\cdot(-4)=9+16=25 \\ \Delta_4=0^2-4\cdot1\cdot(-16)=64 \end{gathered}\)But as you can see, two of them have discriminant zero, so we have to determine in fact which of them have the two roots equal to 4.
In this case, we know that these kind of polynomials are of the form:
\(x^2\pm2ax+a^2=0\)And the option that gives you roots at x = a is exactly:
\(x^2-2ax+a^2=0\)Because it can be factored as:
\((x-a)^2=0\)Therefore the correct answer is:
\(x^2-8x+16\)And it is contained in the option B.
Plz help
What is |5 x -3|?
-15
⊝
-8
⊝
15
⊝
8
Answers
Answer:
What type of math is this
Step-by-step explanation:
Area = 2,800 square meters
2,800
Square meters Find the unknown measure of the rectangle
Answers
When given the area of a rectangle, and one of the sides, the unknown measure of the rectangle would be 40 meters
How to find the area of a rectangle ?To find the area of a rectangle, you can use the formula:
A = l x w
where A is the area of the rectangle, l is the length of the rectangle, and w is the width of the rectangle.
Seeing as you were given the area to be 2, 800 square meters and one of the sides measures 70 meters, the unknown measure of the rectangle would be:
70x Unknown = 2, 800
Unknown = 2, 800 / 70
Unknown measure = 40 meters
Find out more on rectangles at https://brainly.com/question/27035529
#SPJ1
Full question is:
Area = 2,800 square meters
Side A = 70 meters
Find the unknown measure of the rectangle
Rebecca David earns $427.50 per week as a manager at Marlin Department Store. She is married and claimed 1 allowance last year. She hopes to receive a refund on her next tax return by claiming no allowances this year. How much more in withholdings will be deducted weekly if she claims no allowances?
Answers
The amount that is going to be deducted as per withholdings on a per week basis is 61 dollars.
What is withholding tax?The sum of money that an employer withholds from an employee's gross salary and then sends to the government is referred to as withholding tax. In the United States, tax withholding is required of the great majority of workers. The amount withheld is credited against the employee's yearly income tax obligations.
The amount that is earned = 427.5 dollars
The period is 1 week = 7 days
withholding tax = 427.5 / 7
= 61 dollars.
Read more on withholding tax here:https://brainly.com/question/26781826
#SPJ1
The number of calories needed in a daily diet varies directly as the weight of an individual. If 1,050 calories should be consumed daily for a 105-pound person, what is the weight of an individual who consumes 1,370 calories per day?
Answers
Improper Fraction question

Answers
answer is 9/2 as an improper fraction 4(1/2)
4•2 = 8 + 1 = 9
The graph shows the relationship between the width of a sticker and the length of the sticker sold at an art store. Is the relationship represented by the graph a function?
A
function
B
not a function
C
both
D
neither

Answers
Answer:
C both is the right answer
Ferris Wheeler is a trader in entertainment services. The business reported a net loss of $18,800 for the year 2012. At the start of the year the owners’ equity was $378,800, and at the end of the year the equity was $330,000. During the year the owner took goods valued at $10,000 as well as cash for personal use.
What is the amount of cash drawings for the year?
Answers
Answer: $20000
Step-by-step explanation:
The amount of cash drawings for the year will be calculated thus:
Net loss = $18,800
Beginning owner's equity = $378,800
Ending owner's equity = $330,000
Goods withdrazwn by owner = $10,000
The Ending owner's equity is calculated as:
= Beginning owner's equity - Net loss - Goods withdrazwn by owner - Cash withdrawn by owner
We'll then slot in the values given and this will be:
330,000 = 378,800 - 18,800 - 10,000 - Cash withdrawn by owner
330,000 = 350,000 - Cash withdrawn by owner
Cash withdrawn by owner will the be:
= $350000 - $330000
= $20,000
2x {3x [40 - (I0 x 2)]} = ?
Answers
the answer its 120 hope helps you
Two student clubs were selling t-shirts and school notebooks to raise money for an upcoming school event. In the first few minut
notebooks, and made $19. Club B sold 1 t-shirt and 1 notebook, for a total of $8.
-
Use matrices to solve the equation and determine the cost of a t-shirt and the cost of a notebook. Show or explain all necessary:

Answers
Using matrices the simultaneous equation is solved to get x = 3 and y = 5
How to solve the simultaneous equation using matricesThis method required finding determinants in three occasions then dividing
The given equation
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right] \left[\begin{array}{c}x\\y\\\end{array}\right]= \left[\begin{array}{c}19\\8\\\end{array}\right]\)
the determinant is
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right]\)
3 * 1 - 2 * 1 = 3 - 2 = 1
Solving for x
determinant while replacing x values
\(\left[\begin{array}{cc}19&2&\\8&1\\\end{array}\right]\)
19 * 1 - 2 * 8 = 19 - 16 = 3
solving for x = 3/1 = 3
Solving for y
determinant while replacing y values
\(\left[\begin{array}{cc}3&19&\\1&8\\\end{array}\right]\)
3 * 8 - 19 * 1 = 24 - 19 = 5
solving for y = 5/1 = 5
Learn more about simultaneous equations at:
https://brainly.com/question/148035
#SPJ1
Solve the following quadratic inequality x^2+x-6>0
Answers
Answer:
x < -3 or x > 2
Step-by-step explanation:
x² + x - 6 > 0
Convert the inequality to an equation.
x² + x - 6 = 0
Factor using the AC method and get:
(x - 2) (x + 3) = 0
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.
x - 2 = 0
x = 2
x + 3 = 0
x = -3
So, the solution is x < -3 or x > 2
You have a cell phone plan that allows you 800 free minutes and 800 free texts. The base plan costs $55.00. Overage charges are 2 cents per extra minute and 2 cents per extra text message. If you use 899 minutes of talking and 905 text messages, what will be the cost of your bill?
Answers
Extra minutes= 99x0.02=$1.98
Extra messages=105x0.02=$2.10
Total=$2.10+$1.98+$55=$59.08
there was 506 tickets sold for the school play they were either student tickets or adult tickets there was 56 more student tickets sold than adult tickets sold how many adult tickets were sold
Answers
Answer:
A = 228 tickets
Step-by-step explanation:
We need to set up a system of equation to find the number of adult tickets sold, where A represents the adult tickets and S represents the student tickets.
Because the number of adult and student tickets together equals 506, we have A + S = 506.
Because there are 56 more student tickets than adult tickets we have A + 56 = S
And the way the system is already set up allows us to use substitution.
Thus, we have:
\(A + S=506\\A+56 = S\\\\A+A+56 =506\\2A+56=506\\2A=456\\\\A=228\\228+56=S\\278=S\)
The number of student tickets was not necessary to find in this problem, but I found anyway just in case you wanted check the work or wanted to prove the validity of the values.
can someone help me with my work so i can pass
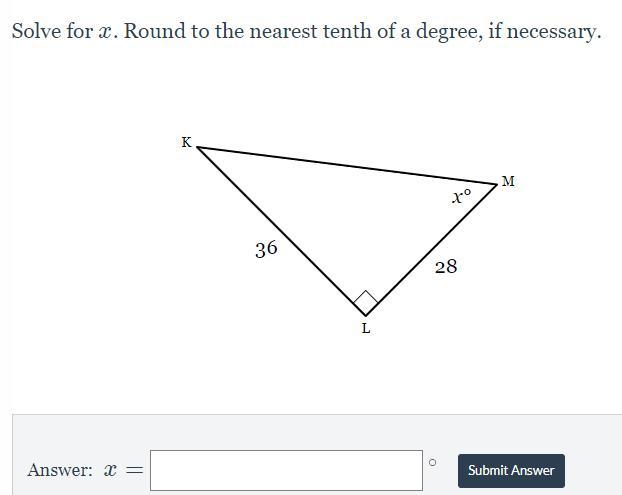
Answers
The measure of the angles are:: x = 20. so, angles are, 20°, 40°, 120°.
Here, we have,
we know that,
The sum of the angles in a triangle add to 180
x+2x+6x = 180
Combine like terms
9x= 180
Divide by 9
9x/9 = 180/9
x = 20.
Hence, The measure of the angles are:: x = 20. so, angles are, 20°, 40°, 120°.
To learn more on angle click:
brainly.com/question/28451077
#SPJ1
complete question:
The sum of the angle measures in a triangle is 180°. The angles of a certain triangle measure x°, 2x°, and 6x°. Solve for x.
NO LINKS!!! URGENT HELP PLEASE!!!
State if the given functions are inverses.
1. g(x) = 4 + (7/2)x
f(x) = 5 - (4/5)x
Find the inverses of each function.
2. g(n) = (8/3)n + 7/3
3. g(x) = 1 - 2x^3
Answers
Answer:
1) The functions are not inverses.
\(\textsf{2)} \quad g^{-1}(n)=&\dfrac{3}{8}n-\dfrac{7}{8}\)
\(\textsf{3)} \quad g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\)
Step-by-step explanation:
Question 1The inverse composition rule states that if two functions are inverses of each other, then their compositions result in the identity function.
Given functions:
\(g(x) = 4 + \dfrac{7}{2}x \qquad \qquad f(x) = 5 - \dfrac{4}{5}x\)
Find g(f(x)) and f(g(x)):
\(\begin{aligned} g(f(x))&=4+\dfrac{7}{2}f(x)\\\\&=4+\dfrac{7}{2}\left(5 - \dfrac{4}{5}x\right)\\\\&=4+\dfrac{35}{2}-\dfrac{14}{5}x\\\\&=\dfrac{43}{2}-\dfrac{14}{5}x\\\\\end{aligned}\) \(\begin{aligned} f(g(x))&=5 - \dfrac{4}{5}g(x)\\\\&=5 - \dfrac{4}{5}\left(4 + \dfrac{7}{2}x \right)\\\\&=5-\dfrac{16}{5}-\dfrac{14}{5}x\\\\&=\dfrac{9}{5}-\dfrac{14}{5}x\end{aligned}\)
As g(f(x)) or f(g(x)) is not equal to x, then f and g cannot be inverses.
\(\hrulefill\)
Question 2To find the inverse of a function, swap the dependent and independent variables, and solve for the new dependent variable.
Calculate the inverse of g(n):
\(\begin{aligned}y &= \dfrac{8}{3}n + \dfrac{7}{3}\\\\n &= \dfrac{8}{3}y + \dfrac{7}{3}\\\\3n &= 8y + 7\\\\3n-7 &= 8y\\\\y&=\dfrac{3}{8}n-\dfrac{7}{8}\\\\g^{-1}(n)&=\dfrac{3}{8}n-\dfrac{7}{8}\end{aligned}\)
Calculate the inverse of g(x):
\(\begin{aligned}y &= 1-2x^3\\\\x &= 1-2y^3\\\\x -1&=-2y^3\\\\2y^3&=1-x\\\\y^3&=\dfrac{1}{2}-\dfrac{1}{2}x\\\\y&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\\end{aligned}\)
Answer:
1.
If the composition of two functions is the identity function, then the two functions are inverses. In other words, if f(g(x)) = x and g(f(x)) = x, then f and g are inverses.
For\(\bold{g(x) = 4 + \frac{7}{2}x\: and \:f(x) = 5 -\frac{4}{5}x}\), we have:
\(f(g(x)) = 5 - \frac{4}{5}(4 + \frac{7}{2}x)\\ =5 - \frac{4}{5}(\frac{8+7x}{2})\\=5 - \frac{2}{5}(8+7x)\\=\frac{25-16-14x}{5}\\=\frac{9-14x}{5}\)
\(g(f(x)) = 4 + (\frac{7}{5})(5 - \frac{4}{5}x) \\=4 + (\frac{7}{5})(\frac{25-4x}{5})\\=4+ \frac{175-28x}{25}\\=\frac{100+175-28x}{25}\\=\frac{175-28x}{25}\)
As you can see, f(g(x)) does not equal x, and g(f(x)) does not equal x. Therefore, g(x) and f(x) are not inverses.
Sure, here are the inverses of the functions you provided:
2. g(n) = (8/3)n + 7/3
we can swap the roles of x and y and solve for y to find the inverse of g(n). In other words, we can write the equation as y = (8/3)n + 7/3 and solve for n.
y = (8/3)n + 7/3
n =3/8*( y-7/3)
Therefore, the inverse of g(n) is:
\(g^{-1}(n) = \frac{3}{8}(n - \frac{7}{3})=\frac{3}{8}*\frac{3n-7}{3}=\boxed{\frac{3n-7}{8}}\)
3. g(x) = 1 - 2x^3
We can use the method of substitution to find the inverse of g(x). We can substitute y for g(x) and solve for x.
\(y = 1 - 2x^3\\2x^3 = 1 - y\\x = \sqrt[3]{\frac{1 - y}{2}}\)
Therefore, the inverse of g(x) is:
\(g^{-1}(x) =\boxed{ \sqrt[3]{\frac{1 - x}{2}}}\)
Ver en español
Pam, the CEO of Zettabyte Tek, set up a $750,000 education fund. She wants to give each employee who takes a computer security class a $350 reimbursement toward the cost of the class. You can use a function to describe the amount of money left in the fund after x employees receive the reimbursement.
Write an equation for the function. If it is linear, write it in the form f(x)=mx+b. If it is exponential, write it in the form f(x)=a(b)x.
Answers
The formula for this linear function is f(x) = mx + b, where m is the slope (in this example, -350), and b is indeed the y-intercept (750,000 in this case).
What does a simple equation represent?An equation expressing the connection between the expressions on either side of a sign. Normally, it has an equal sign and just one variable. such as: 2x - 4 is equal to 2. The variable x is present in the example above.
Workers who complete the computer security course will each receive a reimbursement of $350.
We deduct $350x from of the initial $750,000 to determine how much money will remain inside the education fund once x employee gets the reimbursement.
Thus, f(x) = 750,000 - 350x is the equation again for function that describes that amount of money still in the fund when x employees receive the refund.
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ1
A boat is heading towards a lighthouse, whose beacon-light is 119 feet above the
water. From point A, the boat's crew measures the angle of elevation to the beacon,
5°, before they draw closer. They measure the angle of elevation a second time from
point B at some later time to be 18°. Find the distance from point A to point B.
Round your answer to the nearest foot if necessary.
Answers
Rounding to the nearest foot, the distance from point A to point B is approximately 182 feet.
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles.
Let's assume that the distance from point A to the lighthouse is x feet and the distance from point B to the lighthouse is y feet. Also, let's assume that the height of the boat's crew's eye level is h feet above the water.
From point A, we can use tangent function to find x:
tan(5°) = (119 + h) / x
From point B, we can use tangent function again to find y:
tan(18°) = (119 + h) / y
We want to find the distance between point A and point B, which is the difference between x and y:
distance AB = y - x
We need to eliminate h from these equations to solve for x and y. We can do this by solving for h in one equation and substituting it into the other equation:
h = x tan(5°) - 119
tan(18°) = (119 + x tan(5°) - 119) / y
tan(18°) = x tan(5°) / y
y = x tan(5°) / tan(18°)
distance AB = y - x = x (tan(5°) / tan(18°) - 1)
Now we can plug in the values and use a calculator to find the distance:
distance AB = x (tan(5°) / tan(18°) - 1)
distance AB = x (0.107 - 1)
distance AB = -0.893 x
Since the distance cannot be negative, we know that x must be greater than zero. Therefore, we can ignore the negative sign and solve for x:
x = distance AB / -0.893
Using a calculator, we get:
x ≈ 181.74 feet
Rounding to the nearest foot, the distance from point A to point B is approximately 182 feet.
To learn more about trigonometry from the given link:
https://brainly.com/question/29002217
#SPJ1
Find the volume common to two spheres, each with radius r, if the distance between their centers is r/2. [Hint: It may be helpful to look at the previous question and see how it relates to this one. ] intersectingspheres
Answers
Answer:
The volume common to two spheres is \(V=\frac{27 \pi r^3}{32}\)
Step-by-step explanation:
Let r be the radius of each sphere
We are given that distance between their centers is \(\frac{r}{2}\)
Let \((\frac{-r}{4},0)\) be the center of sphere 1 and \((\frac{r}{4},0)\)be the center of sphere 2 .
Using the disk points
a=0 and b =\(\frac{3r}{4}\)
\((x+(\frac{r}{4}))^2+y^2=r^2\\V=2 \int_{0}^{\frac{3r}{4}} \pi y^2 dx\\V=2 \int_{0}^{\frac{3r}{4}} \pi [r^2-(x+(\frac{r}{4}))^2]dx\\V=\frac{27 \pi r^3}{32}\)
Hence the volume common to two spheres is \(V=\frac{27 \pi r^3}{32}\)
In attached diagram, we can see 2 circumferences with radius r, and separated centers by r/2.
The solution is:
V = (11/12)×π×r³
Let´s call circumferences 1 and 2, by symmetry, rotating area A will produce a volume V₁ identical a V₂, Obtained by rotating area B ( both around x-axis), then the whole volume V will be:
V = 2× V₁
V₁ = ∫π×y²×dx (1)
Now
( x - r/2)² + y² = r² the equation of circumference 1
y² = r² - ( x - r/2)²
Plugging this value in equation (1)
V₁ = ∫π×[ r² - ( x - r/2)²]×dx with integrations limits 0 ≤ x ≤ r/2
V₁ = π×∫ ( r² - x² + (r/2)² - r×x )×dx
V₁ = π× [ r²×x - x³/3 + (r/2)²×x - (1/2) ×r×x²] evaluate between 0 and r/2
V₁ = π× [(5/4)×r²×x - x³/3 - (1/2) ×r×x²]
V₁ = π× [(5/4)×r² × ( r/2 - 0 ) - (1/3)×(r/2)³ - (1/2) ×r×(r/2)²]
V₁ = π× [ (5/8)×r³ - r³/24 - r³/8]
V₁ = π× (11/24)×r³
Then
V = 2× V₁
V = 2×π×11/24)×r³
V = (11/12)×π×r³
Related Link : https://brainly.com/question/14301190

What is the value of 3 ^ -3
Answers
Answer:
\(\frac{1}{27}\)
Step-by-step explanation:
\(3^{-3}\\=\frac{1}{3}^{3}\\=\frac{1}{27}\)
Sphenathi stated that the distance from Bloemfontein to upington is 16.3 show all calculations whether his claim is correct
Answers
The distance between Bloemfontein and Upington is a distance of 582 kilometers. The distance between two cities may vary depending on the route taken, traffic, and other factors. The distance between these two cities is measured in a straight line, which may not be the actual road distance.
To determine the distance between Bloemfontein and Upington, we used the Haversine formula, which computes the shortest distance between two points on the surface of a sphere. We first begin by finding the latitude and longitude of the two cities.Bloemfontein is located at -29.1211° latitude and 26.2140° longitude.Upington is located at -28.4478° latitude and 21.2561° longitude.Using the Haversine formula, we can determine that the distance between the two cities is about 582 kilometers.Sphenathi's statement that the distance from Bloemfontein to Upington is 16.3 kilometers is incorrect. Perhaps they mistakenly calculated the distance between two points within the cities. They could also have made a typographical mistake while writing their statement. Therefore, the statement is false, and the actual distance between Bloemfontein and Upington is 582 kilometers.For such more question on longitude
https://brainly.com/question/28173702
#SPJ8
A pair of standard dice is rolled. Find the probability that the sum of the two dice is greater than 1.
Answers
Answer:
1/1 chance
Step-by-step explanation:
The lowest sum the die could add up to is 2. 2>1
So that means that on every roll, the sum of the two die will add to a number greater than one.
a company finds the total cost of producing 25 items is $8,750, while they can produce 55 items for a total cost of $10,250. they have a revenue of $9,000 by selling 75 items. answer each of the following. enter all answers below using exact numbers, and put equations in slope-intercept form. let x be the number of items. (a) find the production cost (in dollars) per item. $ (b) find the company's linear profit function. p(x)
Answers
(a) The production cost per item can be calculated by dividing the total cost of producing 25 items ($8,750) by the number of items (25). Therefore, the production cost per item is $350 ($8,750 / 25).
(b) The company's linear profit function, p(x), can be expressed in the slope-intercept form, y = mx + b. In this case, the slope (m) is the change in profit (9,000 - 10,250 = -1,250) divided by the change in the number of items (75 - 55 = 20). Therefore, m = -62.5. The y-intercept (b) is the total revenue from selling 75 items ($9,000). Therefore, the linear profit function is: p(x) = -62.5x + 9,000.
The linear profit function suggests that the company's profit decreases by $62.50 for every additional item produced and sold. In other words, the company makes a profit of $9,000 when they produce and sell 75 items, but if they produce and sell 76 items, their profit reduces by $62.50. The equation also suggests that the company will not make any profit (in fact, they will make a loss) when they produce and sell more than 158 items.
To learn more about cost:
https://brainly.com/question/28147009
#SPJ4
Mr. Lewis is 63 years old. He wants to take out a five-year level-term life insurance
policy with a face value $700,000. The monthly premium is $72.
2. If he dies after paying for the policy for 24 months, how much will the insurance
company pay his beneficiaries?
Answers
The amount insurance company will pay is $700000.
We are given that
Age of Mr. lewis= 63
Policy value= $700,000
Now,
If Mr. Lewis dies after paying for the policy for 24 months, he would have paid a total of 24 * $72 = $1728 in premiums. Since he has a five-year level-term life insurance policy with a face value of $700,000, his beneficiaries would receive the full face value of the policy if he dies within the five-year term.
Therefore, by algebra the answer will be $700000.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ1
A student ran a distance of 3 1/2miles each day for 5 days. Then the student ran a distance of 4 1/4 miles each day for the next 5 days. What was the total distance in miles the student ran during these 10 days?
Answers
Answer:
To find the total distance, we need to add up the distance the student ran in the first 5 days and the distance the student ran in the next 5 days.
Distance for the first 5 days = 3 1/2 miles/day × 5 days = 17.5 miles
Distance for the next 5 days = 4 1/4 miles/day × 5 days = 21.25 miles
Total distance = Distance for the first 5 days + Distance for the next 5 days
Total distance = 17.5 miles + 21.25 miles
Total distance = 38.75 miles
Therefore, the student ran a total of 38.75 miles during these 10 days.