Find the radius of a circle with
circumference of 23.55 feet.
Use 3.14 for í.
Hint: C = 2πr
radius = [?] feet please explain your answer so I can understand how to do the rest
![Find The Radius Of A Circle Withcircumference Of 23.55 Feet.Use 3.14 For .Hint: C = 2rradius = [?] Feet](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/3HofDk19rNnSCRdZdxCIrId3KbvbT91F.png)
Answers
Answer:
r = 3.75
Step-by-step explanation:
C = 2(pi)r (write equation)
r = c / 2pi (rearrange for r)
r = 23.55 / 2(3.14) (plug in variables)
r = 23.55 / 6.28 (simplify)
r = 3.75 (solve)
Related Questions
Please show work
Determine the value of each variable

Answers
9514 1404 393
Answer:
k = 56°
Step-by-step explanation:
If b represents a base angle in an isosceles triangle, and 'a' represents the ap.ex angle, then the relation between them is ...
2b +a = 180°
from which we get ...
a = 180° -2b
b = (180° -a)/2
__
The angle at lower right is a base angle of the outside isosceles triangle. Its value is (180° -56°)/2 = 124°/2 = 62°.
The angle marked k is the ap.ex angle of the triangle whose base angle is 62°. We have already seen that the ap.ex angle is 180° -2(62°) = 56°.
k = 56°
_____
We don't see x anywhere on the diagram. The unmarked angle at lower left will be 62° -56° = 6°.
The obtuse angle on the right will be 180°-56°-6° = 118°. The acute angle of that linear pair is the other base angle of the smaller isosceles triangle, so is 62°.
write the equation of the line in fully simplified slope intercept form

Answers
The equation of a line can be written in both slope-intercept form and standard form.
Write the equation of the line in fully simplified slope intercept form?The equation of a line in slope intercept form is written as y = mx + b, where m is the slope of the line, and b is the y-intercept of the line.The simplified form of the equation of a line is obtained by first identifying the slope of the line. The slope of a line is the ratio of the vertical change (rise) over the horizontal change (run). The slope of a line is written as m = (y2 - y1)/(x2 - x1).Next, the y-intercept of the line is found. The y-intercept is the point where the line intersects the y-axis. To find the y-intercept, substitute the slope into the equation of the line and solve for b.Once the slope and y-intercept have been determined, the equation of the line can be written in fully simplified slope intercept form as y = mx + b.For example, if the slope of a line is 4 and the y-intercept is 6, then the equation of the line in slope intercept form is y = 4x + 6.To learn more about slope intercept form refer to:
https://brainly.com/question/1884491
#SPJ1
ace pharmaceutical has developed a drug that it believes will help lower cholesterol and blood pressure at a significantly greater rate than fish oil. researchers wish to test the new drug and compare the results to those of fish oil and of a placebo. a total of 300 volunteers suffering from hypertension and high cholesterol will participate in the study. part a explain how you would carry out this test in a completely randomized experiment.
Answers
The subjects would be randomized at random to receive the new medication, fish oil, or a placebo. The effectiveness of the new variance medicine would next be evaluated by comparing the outcomes of the various therapies.
The test would be conducted using a completely randomized experiment. This means that the 300 volunteers would be randomly assigned to the three different treatments: the new drug, fish oil, or the placebo. This ensures that any differences between the groups can be attributed to the treatments, and not any other factor. The volunteers would be monitored for a period of time, and the results of the treatments would be compared to determine the effectiveness of the new drug. This could be done through measuring changes in cholesterol and blood pressure levels, as well as any side effects of the treatments. In addition, the volunteers’ health and dietary habits should be monitored to ensure that any differences between the treatments are not caused by any other factors.
Learn more about variance here
https://brainly.com/question/13708253
#SPJ4
Write a rule for the translation.
A. ( x - 1, y + 2 )
B. ( x + 2, y - 1 )
C. ( x - 2, y + 1 )
D. ( x + 1, y - 2 )

Answers
Answer:
Option B. ( x + 2, y - 1 ) is the correct answer.
Step-by-step explanation:
First of all, we have to write the coordinates of vertices of both triangles and then compare the respective vertices to find the rule,
So the vertices are:
A(-4,2) , B(-3,4) and C(-1,1)
A'(-2,1), B'(-1,3) and C'(1,0)
By comparing respective vertices we can observe that
A(-4,2) => (x+2,y-1) => A'(-2,1)
B(-3,4) => (x+2,y-1) => B'(-1,3)
C(-1,1) => (x+2,y-1) => C'(1,0)
Hence,
Option B. ( x + 2, y - 1 ) is the correct answer.
2) The representative agent lives for infinite periods (0,1,2,…) and receives exogenous incomes of y0,y1,y2,…, respectively. The lifetime present discounted value of utility is given by: ∑t=0[infinity]βtln(ct) with β(<1) being the discount factor and ct is consumption at time t. The agent is allowed to save or borrow at the real interest rate r, but she cannot die with debt or wealth. Assume also that the initial wealth is zero. a. Solve the optimization problem of the agent using the period-by-period budget constraints. In particular, show the Euler equation. b. Using the given functional form, write the Euler equation between time 1 and time 3 . In other words, show how c1 and c3 are related. c. Write the present discounted value of optimal lifetime consumption as a function of c0 (and, potentially, other parameters or exogenous variables). d. Write the present discounted value of optimal lifetime utility as a function of c0 (and, potentially, other parameters or exogenous variables). e. Find the present discounted value of lifetime income as a function of y0 (and, potentially, other parameters or exogenous variables) when income is growing each period at the rate of γ, where 0<γ0 ? Explain!
Answers
a. U'(ct) = β(1 + r)U'(ct+1). This equation is known as the Euler equation, which represents the intertemporal marginal rate of substitution between consumption at time t and consumption at time t+1.
b. U'(c1) = β(1 + r)^2U'(c3). This relationship shows that the marginal utility of consumption at time 1 is equal to the discounted marginal utility of consumption at time 3.
c. C0 = ∑t=0[infinity](β(1 + r))^tct. This equation represents the sum of the discounted values of consumption at each period, where the discount factor β(1 + r) accounts for the diminishing value of future consumption.
d. U0 = ∑t=0[infinity](β(1 + r))^tln(ct). This equation represents the sum of the discounted values of utility at each period, where the discount factor β(1 + r) reflects the time preference and the logarithmic utility function captures the agent's preference for consumption.
Y0 = y0 + (1 + γ)y1 + (1 + γ)^2y2 + ..., where γ represents the growth rate of income.
a. The optimization problem of the representative agent involves maximizing the present discounted value of utility subject to the period-by-period budget constraint. The Euler equation is derived as follows:
At each period t, the agent maximizes the utility function U(ct) = ln(ct) subject to the budget constraint ct = (1 + r)wt + yt, where wt is the agent's wealth at time t. Taking the derivative of U(ct) with respect to ct and applying the chain rule, we obtain: U'(ct) = β(1 + r)U'(ct+1). This equation is known as the Euler equation, which represents the intertemporal marginal rate of substitution between consumption at time t and consumption at time t+1.
b. The Euler equation between time 1 and time 3 can be written as U'(c1) = β(1 + r)U'(c2), where c1 and c2 represent consumption at time 1 and time 2, respectively.
Similarly, we can write the Euler equation between time 2 and time 3 as U'(c2) = β(1 + r)U'(c3). Combining these two equations, we fin
d U'(c1) = β(1 + r)^2U'(c3). This relationship shows that the marginal utility of consumption at time 1 is equal to the discounted marginal utility of consumption at time 3.
c. The present discounted value of optimal lifetime consumption can be written as C0 = ∑t=0[infinity](β(1 + r))^tct. This equation represents the sum of the discounted values of consumption at each period, where the discount factor β(1 + r) accounts for the diminishing value of future consumption.
d. The present discounted value of optimal lifetime utility can be written as U0 = ∑t=0[infinity](β(1 + r))^tln(ct).
This equation represents the sum of the discounted values of utility at each period, where the discount factor β(1 + r) reflects the time preference and the logarithmic utility function captures the agent's preference for consumption.
e. The present discounted value of lifetime income, denoted as Y0, can be expressed as Y0 = y0 + (1 + γ)y1 + (1 + γ)^2y2 + ..., where γ represents the growth rate of income. The income in each period is multiplied by (1 + γ) to account for the increasing income over time.
This assumption of income growth allows for a more realistic representation of the agent's economic environment, where income tends to increase over time due to factors such as productivity growth or wage increases.
for such more questions on equation
https://brainly.com/question/17145398
#SPJ8
Given the following proposition:
[(X ⊃ A) • (B ⊃ ∼ Y)] ⊃ [(B ∨ Y) • (A ⊃ X)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 2A.
a.
True.
b.
False.
Answers
Therefore, the truth value of Proposition 2A is False.
To determine the truth value of Proposition 2A, let's substitute the given truth values for the variables:
A = True
B = True
X = False
Y = False
Now let's evaluate the truth value of each component of the proposition:
(X ⊃ A) • (B ⊃ ∼ Y):
(False ⊃ True) • (True ⊃ ∼ False)
(True ⊃ True) • (True ⊃ True)
True • True
True
(B ∨ Y) • (A ⊃ X):
(True ∨ False) • (True ⊃ False)
True • False
False
[(X ⊃ A) • (B ⊃ ∼ Y)] ⊃ [(B ∨ Y) • (A ⊃ X)]:
True ⊃ False
False
To know more about Proposition,
https://brainly.com/question/31979370
#SPJ11
The difference of the same side interior angles of two parrelels lines is 50 degrees find all angles
Answers
Answer:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
Step-by-step explanation:
Angle 1: Same-side interior angle of Line 1
Angle 2: Same-side interior angle of Line 2
We know that the difference between the angles is 50 degrees. Since the angles are supplementary, we can write the equation:
Angle 1 + Angle 2 = 180
Now, we need to express the difference between the angles in terms of Angle 1 or Angle 2. We can choose either angle, so let's express it in terms of Angle 1:
Angle 1 - Angle 2 = 50
We can rewrite this equation as:
Angle 1 = 50 + Angle 2
Now substitute this expression for Angle 1 into the first equation:
(50 + Angle 2) + Angle 2 = 180
Combine like terms:
2Angle 2 + 50 = 180
Subtract 50 from both sides:
2Angle 2 = 130
Divide by 2:
Angle 2 = 65
Now substitute this value back into the equation for Angle 1:
Angle 1 = 50 + Angle 2
Angle 1 = 50 + 65
Angle 1 = 115
Therefore, the angles are as follows:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
PLEASE HELP IM BEGGING Ira B. Scholar, that bizarre math teacher, put the figure at right on a recent test and said,
"If the perimeter is 25, solve for x." Show Ira B. that such a figure does not exist. Use algebra and
explain your result (why perimeter cannot equal 25).
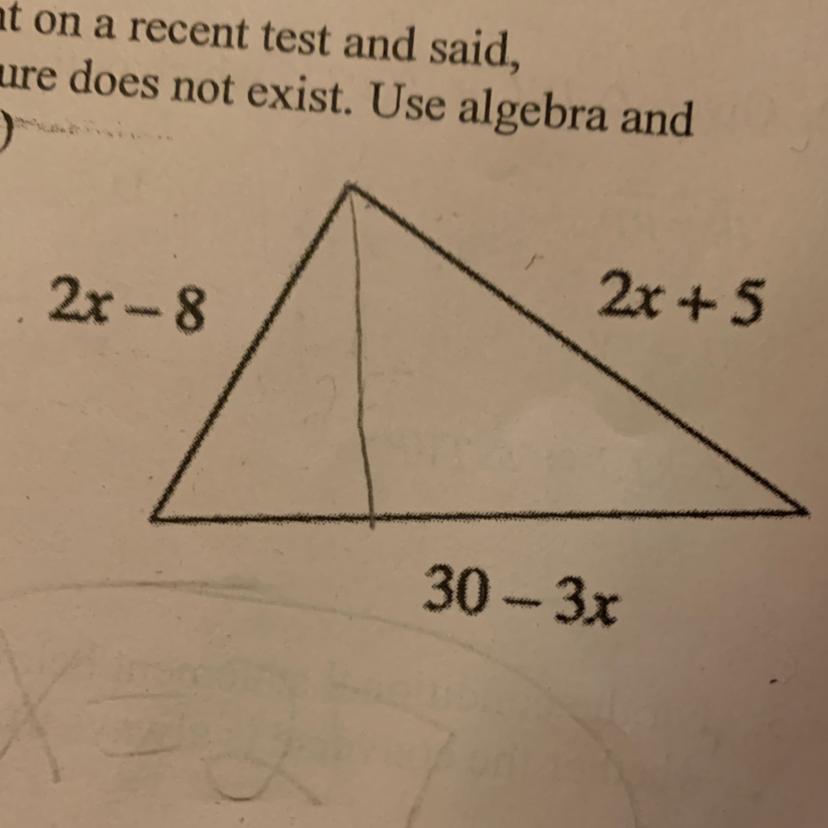
Answers
Answer:
The perimeter is the distance all the way around the outside of a 2D shape. To calculate the perimeter, sum the lengths of all the sides.
Therefore, perimeter of the triangle = (2x - 8) + (2x + 5) + (30 - 3x)
Collect like terms: 2x + 2x - 3x - 8 + 5 + 30
Combine like terms: x + 27
Therefore, perimeter of triangle = x + 27
We are told that the perimeter is 25:
x + 27 = 25
Subtract 27 from both sides: x = -2
If x = -2, then the side with equation 2x - 8 = (2 x -2) - 8 = -12
A length cannot be negative, therefore the perimeter cannot equal 25.
There is £80 in a pot which is shared out amongst 3 people. Anne gets £20 Mark gets £35 and Ben gets £25. What ratio of the money do all of the people get?
Answers
= 4 : 7 : 5 ( total 16 parts )
Anne = 4/16 x £80 = £20
Mark = 7/16 x £80 = £35
Ben = 5/16 x £80 = £25
The 16 oz jar costs per oz. and the 12oz. Jar costs per oz. Slgmund should buy the lar of mayonnaise.
Answers
Based on the given information, the cost per ounce of the 16 oz jar and the 12 oz jar is not provided. Therefore, it is not possible to determine which jar of mayonnaise Sigmund should buy.
In order to compare the cost of the two jars of mayonnaise and determine which one Sigmund should buy, we need to know the price per ounce for each jar. Without this information, we cannot make a conclusive decision.
The cost per ounce is essential because it allows us to compare the prices accurately. For example, if the 16 oz jar costs $3 and the 12 oz jar costs $2.50, we can calculate the cost per ounce for each jar. The cost per ounce for the 16 oz jar would be $3 divided by 16 oz, which is $0.1875 per ounce. Similarly, the cost per ounce for the 12 oz jar would be $2.50 divided by 12 oz, which is approximately $0.2083 per ounce.
With this information, we can determine that the 16 oz jar is more cost-effective as it has a lower cost per ounce compared to the 12 oz jar. However, without the specific prices per ounce provided in the given information, it is impossible to determine which jar of mayonnaise Sigmund should buy.
Learn more about ounce here:
https://brainly.com/question/29374025
#SPJ11
*EASY 7TH GRADE MATH*
QUESTION ABOVE
• First answer shall be marked brainliest •
Find the surface area of the prism.

Answers
Answer:
2880
Step-by-step explanation:
The base is made up of two triangles and a square, if that makes sense. Finding the area of a triangle is (base x height)/2.
The base of the tiny triangle is 4 because there is 8 inches extra to the 10 inch square. 10 x 4 = 40.
Now we have a 10 by 10 square: 10 x 10 = 100.
So, the area of the trapezoid is 140. There are two trapezoids in this prism, so both bases are 280.
The surface area of the sides are solved by 12 x 50 = 600. Together, the sides equal 1200.
The top is solved by 10 x 50 = 500.
The bottom is solved by 18 x 50 = 900.
Add them all together: 280 + 1200 + 500 + 900 = 2,880
If+you+invest+$100+at+an+interest+rate+of+15%,+how+much+will+you+have+at+the+end+of+eight+years?
Answers
Answer:
$305.9022863 or $305.90 (rounded to 2 decimal places)
Step-by-step explanation:
It is a compound interest, meaning an interest accumulates on an initial amount every period. The formula
A= P(1+R)^n
A= the total amount P=Initial amount R= rate n=time period
P=$100 R=15% or 0.15(decimal) n=8 (years)
A= 100 (1.15)^8
A= 100(3.059022863)
A=305.9022863
The amount you will have after 8 years is $220
Calculating simple interestThe formula for calculating simple interest is expressed as:
SI =PRT
P is the principal = $100
T is the time = 8 years
R is the rate. = 15%
SI = 100 * 8 * 0.15
SI = $120
Amount after 8years = $100 + $120
Amount after 8years = $220
Hence the amount you will have after 8 years is $220
Learn more on interest here: https://brainly.com/question/2151013
#SPJ12
Consider the given pseudo code. Write the function T(n) in terms of the number of operations, and then give the asymptotic (big Oh) complexity of the algorithm, show all the work you do. [ write the summation formula and solve it, or use the "Look for pattern"method. a. Matrix Multiplication
Answers
The function T(n) in terms of the number of operations is:
T(n) = 2n^3 + 3n^2 + 2n + 1 and the asymptotic complexity of the matrix multiplication algorithm is O(n^3).
To analyze the provided pseudo code for matrix multiplication and determine the function T(n) in terms of the number of operations, we need to examine the code and count the number of operations performed.
The pseudo code for matrix multiplication may look something like this:
```
MatrixMultiplication(A, B):
n = size of matrix A
C = empty matrix of size n x n
for i = 1 to n do:
for j = 1 to n do:
sum = 0
for k = 1 to n do:
sum = sum + A[i][k] * B[k][j]
C[i][j] = sum
return C
```
Let's break down the number of operations step by step:
1. Assigning the size of matrix A to variable n: 1 operation
2. Initializing an empty matrix C of size n x n: n^2 operations (for creating n x n elements)
3. Outer loop: for i = 1 to n
- Incrementing i: n operations
- Inner loop: for j = 1 to n
- Incrementing j: n^2 operations (since it is nested inside the outer loop)
- Initializing sum to 0: n^2 operations
- Innermost loop: for k = 1 to n
- Incrementing k: n^3 operations (since it is nested inside both the outer and inner loops)
- Performing the multiplication and addition: n^3 operations
- Assigning the result to C[i][j]: n^2 operations
- Assigning the value of sum to C[i][j]: n^2 operations
Total operations:
1 + n^2 + n + n^2 + n^3 + n^3 + n^2 + n^2 = 2n^3 + 3n^2 + 2n + 1
Therefore, the function T(n) in terms of the number of operations is:
T(n) = 2n^3 + 3n^2 + 2n + 1
To determine the asymptotic (big O) complexity of the algorithm, we focus on the dominant term as n approaches infinity.
In this case, the dominant term is 2n^3. Hence, the asymptotic complexity of the matrix multiplication algorithm is O(n^3).
To know more about asymptotic complexity refer here:
https://brainly.com/question/30214690#
#SPJ11
Please help!! I need to get this! Brainliest For Right Anwser!

Answers
Answer:
Data set A best fit by the regression line.
Answer:
Data Set C.
Step-by-step explanation:
Well just even by common sense, the line for "data set A" is not good for the points on the graph
What is the lateral surface area of the square pyramid represented by this net?
Enter your answer in the box
__ft²

Answers
Answer:
If you know the answer to this just put it down below
Step-by-step explanation:

Please answer!!! I’ll make brainliest

Answers
Answer:
10.3
Step-by-step explanation:
The question is asking to find the length of the hypotenuse of the triangle. This requires us to use the Pythagorean theorem. The legs measure 9 and 5, so we use these to solve for c.
\(9^{2} + 5^{2} =c^{2} \\81 + 25 = c^{2} \\106 = c^{2} \\\)
We find the square root of both sides to find the value of c.
10.295 ≈ c
Rounded to the nearest tenth, c ≈ 10.3. The answer is 10.3
If a is a bigger number than b what will (b - a) give you? positive or negative
Answers
Answer:negative
a>b
b-a<0 (negative)
only 18 percent of the peices in the box were unpainted. if 738 oieces were painted, how many pieces were in the box?
Answers
If 18% of the pieces in the box were unpainted, that means 82% of the pieces in the box were painted.
And since 738 pieces were painted, that number comprises 82% of the total number of pieces.
Therefore, the number of pieces in the box was : 738 : 82% = 900 (pieces)
what is the difference of the polynomial, write your answer in descending order. (3x^2 – 3x + 6) – (5x^2 + 2x + 9)
Answers
Answer:
-2x^2 -5x -3
Step-by-step explanation:
(3x^2 – 3x + 6) – (5x^2 + 2x + 9)
Distribute the minus sign
(3x^2 – 3x + 6) – 5x^2 - 2x - 9
Combine like terms
3x^2 – 5x^2 - 2x– 3x - 9+ 6
-2x^2 -5x -3
forestry ranger is in a stand 200 feet in the air. There is an angle of
depression of 35 degrees to a campfire. How far is it from the base of the
stand to the campfire?
Hunter ic a deer stand 10 feet above the ground. There is an angle c
Answers
The distance from the base of the stand to the campfire is 285.6 feet.
The angle of depression of 35 degrees.
Let's denote the distance from the base of the stand to the campfire as "x."
Since we know that,
The values of all trigonometric functions depending on the ratio of sides in a right-angled triangle are defined as trigonometric ratios. The trigonometric ratios of any acute angle are the ratios of the sides of a right-angled triangle with respect to that acute angle.
Using the tangent function, we have:
tan(35 degrees) = opposite/adjacent
tan(35 degrees) = 200/x
To find the value of x, we can rearrange the equation:
x = 200 / tan(35 degrees)
x ≈ 200 / 0.7002
x ≈ 285.6 feet
Therefore, the distance from the base of the stand to the campfire is 285.6 feet.
Learn more about Trigonometry here:
brainly.com/question/12068045
#SPJ1
If I drive 250 miles on Tuesday and 180 miles on Wednesday. How many miles did I drive in all? (Multiply)
Answers
The miles drive on Tuesday is , 250 miles.
The miles drive on Wednesday is , 180 miles.
The total miles drive on Tuesday and Wednesday is, the sum of drive on Tuesday and Wednesday.
\(S=250+180\)\(S=430.\)Thus, the total miles drive on Tuesday and Wednesday is, 430 miles.
Solve algebraically.
16*4^(x-2) = 64^-2x
Answers
According to given information, answer is \(x = 2/3\).
The equation is \(16 * 4^{(x - 2)} = 64^{-2x}\).
Let's begin by simplifying both sides of the equation \(16 * 4^{(x - 2)} = 64^{-2x}\).
We can write \(64^{-2x}\) in terms of \(4^{(x - 2}\).
Observe that 64 is equal to \(4^3\).
So, we have \(64^{(-2x)} = (4^3)^{-2x} = 4^{-6x}\)
Hence, the given equation becomes \(16 * 4^{(x - 2)} = 4^{(-6x)}\)
Let's convert both sides of the equation into a common base and solve the resulting equation using the laws of exponents.
\(16 * 4^{(x - 2)} = 4^{(-6x)}\)
\(16 * 2^{(2(x - 2))} = 2^{(-6x)}\)
\(2^{(4 + 2x - 4)} = 2^{(-6x)}\)
\(2^{(2x)} = 2^{(-6x)}\)
\(2^{(2x + 6x)} = 12x\)
Hence, \(x = 2/3\).
Answer: \(x = 2/3\).
To know more about equation, visit:
https://brainly.com/question/29657983
#SPJ11
For the following question, show representation, your initial equations, your algebra work, symbolic answer, and units check.
A dog is sitting at an initial position of D1= (50 m North, 10 m East) from her home. She moves in a straight line until she is at a final position of D2 = ( 5 m North, 35 m East) from her home. It takes her 15 seconds to move from the initial position to the final position; find the magnitude of her average velocity vector.
Answers
The magnitude of the average velocity vector is approximately 3.651 m/s.
To find the magnitude of the average velocity vector, we need to calculate the displacement and divide it by the time taken.
Representation:
Initial position: D1 = (50 m North, 10 m East)
Final position: D2 = (5 m North, 35 m East)
Time taken: t = 15 seconds
Equations:
Displacement vector (ΔD) = D2 - D1
Average velocity vector (\(V_{avg}\)) = ΔD / t
Algebra work:
ΔD = D2 - D1
= (5 m North, 35 m East) - (50 m North, 10 m East)
= (-45 m North, 25 m East)
|ΔD| = √((-45)^2 + 25^2) [Magnitude of the displacement vector]
\(V_{avg}\) = ΔD / t
= (-45 m North, 25 m East) / 15 s
= (-3 m/s North, 5/3 m/s East)
|\(V_{avg}\)| = √((-3)^2 + (5/3)^2) [Magnitude of the average velocity vector]
Symbolic answer:
The magnitude of the average velocity vector is approximately 3.651 m/s.
Units check:
The units for displacement are in meters (m) and time in seconds (s). The average velocity is therefore in meters per second (m/s), which confirms the units are consistent with the calculation.
Therefore, the magnitude of the average velocity vector is approximately 3.651 m/s.
Learn more about vector here: https://brainly.com/question/24256726
#SPJ11
Suppose a and b are mutually exclusive events, and that p(b)=0.48 and p(a or b)=0.98. find p(a).
Answers
The value of p(a) is 0.5
Mutually exclusive events are those events that do not occur at the same time
Given,
The a and b are mutually exclusive events
P(a AND b)=0
P(a)=0.48
p(a or b)=0.98
We know that,
P(a or b)=P(a)+P(b)-P(a AND b)
P(a or b)=P(a)+P(b)-0
P(a or b)=P(a)+P(b)
P(a)=P(a or b)-P(b)
Substitute the given values
P(a)= 0.98-0.48
P(a)=0.5
Hence, the value of P(a) is 0.5
Learn more about Mutually exclusive events here
brainly.com/question/5492865
#SPJ4
Which expression is equivalent to 5y^-3

Answers
Answer:
5/y^3
Step-by-step explanation:
For each of the following scenarios, determine if a confidence interval for a single population or between two populations is appropriate in the context of answering the proposed question: A researcher wants to determine whether the height of 50 twins ( 25 sets of twins) is significantly different than 70 inches. The Environmental Protection Agency is looking to compare the average ages of Coastal Redwoods and Giant Sequoias in Californian National Parks and Forests. A UCSB student wants to get a 'likely" range for the average height of waves at campus point beach. UCSB wants to compare the income of students before and after graduating from the school. The Economics department studies whether student GPAs are different for Seniors and Freshmen in the department.
Answers
1. A confidence interval for the single population of the 50 twins is necessary to determine the average height and likely range.
2. A confidence interval between the two populations is necessary to compare the average ages of the two different tree species.
3. A confidence interval for the single population of the waves at the beach is necessary to determine the average height and likely range.
4. A confidence interval between the two populations is necessary to compare the incomes of the students before and after graduating.
5. A confidence interval between the two populations is necessary to compare the average GPAs of the Senior and Freshmen students.
For the first scenario, a confidence interval for a single population is appropriate in the context of answering the proposed question. The researcher wants to determine whether the height of 50 twins (25 sets of twins) is significantly different than 70 inches, and therefore a confidence interval for the single population of the 50 twins is necessary to determine the average height and likely range.
For the second scenario, a confidence interval between two populations is appropriate in the context of answering the proposed question. The Environmental Protection Agency is looking to compare the average ages of Coastal Redwoods and Giant Sequoias in Californian National Parks and Forests, and therefore a confidence interval between the two populations is necessary to compare the average ages of the two different tree species.
For the third scenario, a confidence interval for a single population is appropriate in the context of answering the proposed question. A UCSB student wants to get a "likely" range for the average height of waves at Campus Point Beach, and therefore a confidence interval for the single population of the waves at the beach is necessary to determine the average height and likely range.
For the fourth scenario, a confidence interval between two populations is appropriate in the context of answering the proposed question. UCSB wants to compare the income of students before and after graduating from the school, and therefore a confidence interval between the two populations is necessary to compare the incomes of the students before and after graduating.
For the fifth scenario, a confidence interval between two populations is appropriate in the context of answering the proposed question. The Economics department studies whether student GPAs are different for Seniors and Freshmen in the department, and therefore a confidence interval between the two populations is necessary to compare the average GPAs of the Senior and Freshmen students.
To know more about confidence interval: https://brainly.com/question/29576113
#SPJ11
Mrs.Galicia bakes and then sells cookies and brownies from her bakery. Her revenue for each baked good (in
dollars) is modeled by the equations, where x is the number of days since the bake goods started to sell.
Brownies: M (d) = 2x² + 8x - 4
Cookies: R(d) = 2x + 4
(a) Solve the system algebraically. After how many days is the revenue for each item the same? Show
your work and explain your answer.
(b) Graph this system to show both solutions. Label each axis appropriately.
Answers
a) After 1 day, the revenue for each item is the same.
b) Graph is shown in the attachment.
What is an equation?
An equation is a mathematical statement that proves two mathematical expressions are equal in algebra, and this is how it is most commonly used. In the equation 3x + 5 = 14, for instance, the two expressions 3x + 5 and 14 are separated.
M(d) = 2x² + 8x - 4
R(d) = 2x + 4
a) Find x by taking y=M(d)=R(d). ( same revenue=y)
y= 2x² + 8x - 4
y= 2x + 4
This shows that right-side expressions are equal.
2x² + 8x - 4 = 2x + 4
2x² + 8x - 4 - 2x - 4=0
2x² +6x-8=0
Find the factors
2(x-1)(x+4)=0
x-1=0, x+4=0
x= 1, x=-4
consider positive value for days
So, after 1 day, the revenue for each item is the same
b) The equations:
y= 2x² + 8x - 4
y= 2x + 4
By taking some random values for x and finding the corresponding y values, we get the ordered pairs in the form of (x,y).
By plotting and joining those points, we get the graph as shown in the attachment.
To learn more about the equation from the given link
https://brainly.com/question/28218072
#SPJ1

What expression is equivalent to 7.2x7.2x7.2
Answers
Step-by-step explanation: 7.2^3 or 7.2 cubed=373.248. I hope I helped.
what percentage of the variation in y can be explained by the corresponding variation in x and the least-squares line?
Answers
The percentage of the variation in y can be explained by the corresponding variation in x and the least - squares line
The value of the coefficient of determination r2 = 0.9617*0.9617 = 0.9249
percentage of the variation in y can be explained by the corresponding variation in x and the least - squares line is = 92.49%
So, percentage is unexplained = (100 - 92.49)%
= 7.51%
Therefore, the percentage of the variation in y that can be explained by the corresponding variation in x and the least-squares line is 92.49% . The percentage which is unexplained is 7.51% i.e. (100%−92.49%) .
Hence the variation in X and the least-squares line is 7.51%
To learn more about percentage, click here https://brainly.com/question/24877689
#SPJ4
Lal less than 4,5 minoten (b) less than 2.5 minutes
Answers
The probabilities, using the normal distribution, are given as follows:
a) Less than 4.5 minutes: 0.7486 = 74.86%.
b) Less than 2.5 minutes: 0.0228 = 2.28%.
How to obtain the probabilities with the normal distribution?The parameters for the normal distribution in this problem are given as follows:
\(\mu = 4, \sigma = 0.75\)
The z-score formula for a measure X is given as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The probability is item a is the p-value of Z when X = 4.5, hence:
Z = (4.5 - 4)/0.75
Z = 0.67
Z = 0.67 has a p-value of 0.7486.
The probability is item b is the p-value of Z when X = 2.5, hence:
Z = (2.5 - 4)/0.75
Z = -2
Z = -2 has a p-value of 0.0228.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ4

Lal is less than 675 minutes and (b) is less than 375 minutes.
The given statement is Lal is less than 4.5 minutes and (b) is less than 2.5 minutes.
Let us assume Minoten = 150
Therefore, Lal is less than 4.5 minutes = 150 × 4.5 = 675
and (b) is less than 2.5 minutes = 150 × 2.5 = 375
Therefore, Lal is less than 675 minutes, and (b) is less than 375 minutes.
Note:
Minoten is not used anywhere in the question except for as an additional term in the prompt.
learn more about minutes at:
https://brainly.com/question/27388265
#SPJ11