Find the area of the square (A = length width) field. Write an expression which
represents the area of this rectangle, then simplify the expression.
- (x + 4) feet
Answers
The area of a square is given by the formula A = s^2, where s is the length of one side of the square. Since the field is a square, we can write the expression for its area as A = s^2, where s is the length of one side of the square. We are given that one side of the square is (x + 4) feet, so we can substitute s = x + 4 into the expression for the area to get A = (x + 4)^2.
To simplify the expression for the area of the square, we can expand the square of a binomial as follows:
A = (x + 4)^2
= x^2 + 8x + 16
So, the area of the square field is given by the expression x^2 + 8x + 16 square feet.
Learn more about binomials here:- brainly.com/question/30339327
#SPJ11
Related Questions
What is the image of (-6,-5) after a reflection over the x-axis?
Answers
Answer:
6,5
Step-by-step explanation:
CAN SOMEONE HURRY AND DO THIS AND TY !!!!!

Answers
Answer:
8.324
Step-by-step explanation:
The 8 serves as the first digit and the "and " represents a decimal point the remaining numbers go behind that decimal point therefore 8.324.
given f(x)=x^2+2x-5 and the values of the linear function g(x) in the table, what is the range of (f+g)(x)
x: -6 -3 -1 4
g(x): 16 10 6 -4
Answers:
(infinity,1]
[-1,1]
R

Answers
The range of the function (f+g)(x) = x² - 1 will be ( -1, ∞ ). The correct option is B.
What are a domain and range?The range of values that we are permitted to enter into our function is known as the domain of a function.
The x values for a function like f make up this set (x). A function's range is the set of values it can take as input. After we enter an x value, the function outputs this set of values.
Given that the function is f(x) = x²+2x-5. The function g(x) will be calculated by the data given in the table.
x -6 -3 -1 4
g(x) 16 10 6 -4
The function g(x) will be:-
g(x) = mx + c
m = ( 10 - 16 ) / ( -3 + 6 )
m = -6 / 3
m = -2
c = y - mx
c = 10 - 6
c = 4
g(x) = -2x + 4
The function ( f + g)(x) will be:-
( f + g)(x) = f(x) + g(x)
( f + g)(x) = x²+ 2x - 5 - 2x + 4
( f + g)(x) = x² - 1
At x = 0, the value ( f + g)(x) is -1. The range of the function is ( -1, ∞).
To know more about domain and range follow
https://brainly.com/question/2264373
#SPJ1

Pleaseeeee answer correctly !!!!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!

Answers
Answer:
let the third side be x
Using pythagoras theorem we get,
(58)^2 = (42)^2 + (x)^2
3364=1764+x^2
x^2=3364-1764
x^2= 1600
x=√(1,600)
x=40
\(\pink{\sf Third \: side \: of \: the \: triangle = 40}\)
Solution :As, the given triangle is a right angled triangle,
Hence, We can use the Pythagoras' Theorem,
\(\star\:{\boxed{\sf{\pink {H^{2} = B^{2} + P^{2}}}}}\)
Here,
H = Hypotenuse of triangleB = Base of triangle P = Perpendicular of triangleIn given triangle,
Base = 42Hypotenuse = 58Perpendicular = ?Now, by Pythagoras' theorem,
\(\star\:{\boxed{\sf{\pink {H^{2} = B^{2} + P^{2}}}}}\)
\( \sf : \implies (58)^{2} = (42)^{2} + P^{2}\)
\( \sf : \implies 58 \times 58 = 42 \times 42 + P^{2} \)
\( \sf : \implies 3364 = 1764 + P^{2}\)
\( \sf : \implies P^{2} = 3364 - 1764\)
\( \sf : \implies P^{2} = 1600\)
By squaring both sides :
\( \sf \sqrt{P^{2}} = \sqrt{1600}\)
\( \sf : \implies P^{2} = \sqrt{1600}\)
\( \sf : \implies P^{2} = \sqrt{(40)^{2}}\)
\( \sf : \implies P^{2} = 40 \)
\(\pink{\sf \therefore \: Third \: side \: of \: the \: triangle \: is \: 40}\)
━━━━━━━━━━━━━━━━━━━━━
On the graph below, draw any line with a slope of *positive* 2 and draw any line with a slope of *negative* 2.
Answers
Refer to the image for the graph of the lines.
The common form of the equation of a line is y = mx + c, where m is the slope of the line and c is a constant.
We need to draw any line with a slope m = 2, and
another line with a slope m = -2.
Disclaimer: Let us assume that the constant c = 0.
Then the equation to the line with a slope of "positive" 2 is given by
y = 2x
Then the equation to the line with a slope of "negative" 2 is given by
y = -2x
Refer to the attached image for the graph of the lines with the slope of "positive" 2 and "negative" 2.
f: green line indicates a line with a slope of "positive" 2.
g: blue line indicates a line with a slope of "negative" 2.
Learn more at:
https://brainly.com/question/28360812
#SPJ9

ASAP! I’m so confused! Please help me on the problem in the picture, thanks!!!!
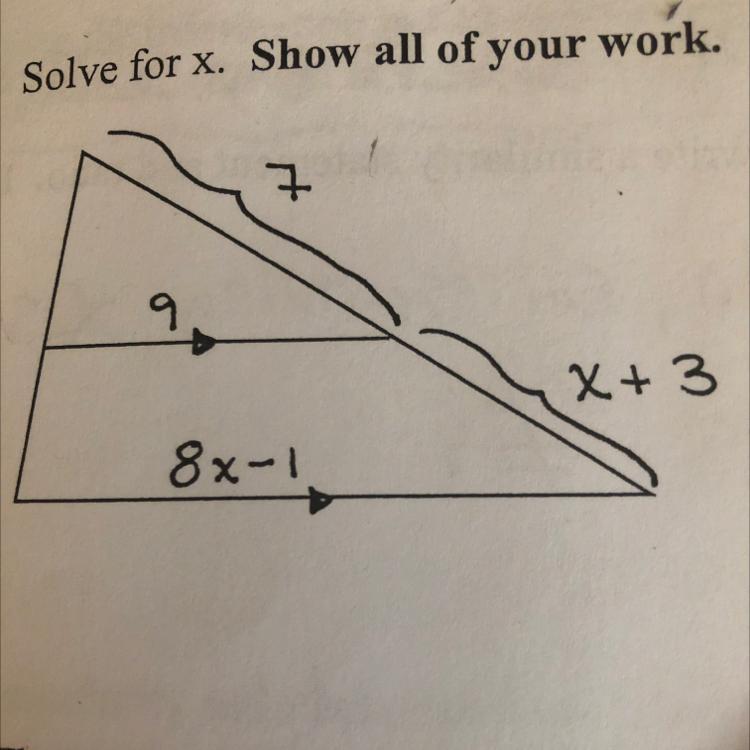
Answers
Given : tan A =4/3, find : cosec A / cot A - sec A
Answers
The value of cosec A / cot A - sec A, we'll first express cosec A, cot A, and sec A in terms of the given value of tan A.The value of cosec A / cot A - sec A, using the given value of tan A = 4/3, is 1 + √(9/7)/3.
We know that cosec A is the reciprocal of sin A, and sin A is the reciprocal of cosec A. Similarly, cot A is the reciprocal of tan A, and sec A is the reciprocal of cos A.
Using the Pythagorean identity, sin^2 A + cos^2 A = 1, we can find the value of cos A. Since tan A = 4/3, we can find sin A as well.
Given:
tan A = 4/3
Using the Pythagorean identity:
sin^2 A + cos^2 A = 1
We can solve for cos A as follows:
(4/3)^2 + cos^2 A = 1
16/9 + cos^2 A = 1
cos^2 A = 1 - 16/9
cos^2 A = 9/9 - 16/9
cos^2 A = -7/9
Taking the square root of both sides, we get:
cos A = ± √(-7/9)
Since cos A is positive in the first and fourth quadrants, we take the positive square root:
cos A = √(-7/9)
Now, using the definitions of cosec A, cot A, and sec A, we can find their values:
cosec A = 1/sin A
cot A = 1/tan A
sec A = 1/cos A
Substituting the values we found:
cosec A = 1/sin A = 1/√(1 - cos^2 A) = 1/√(1 - (-7/9)) = 1/√(16/9) = 1/(4/3) = 3/4
cot A = 1/tan A = 1/(4/3) = 3/4
sec A = 1/cos A = 1/√(-7/9) = -√(9/7)/3
Now, let's calculate the expression cosec A / cot A - sec A:
cosec A / cot A - sec A = (3/4) / (3/4) - (-√(9/7)/3)
= 1 - (-√(9/7)/3)
= 1 + √(9/7)/3
Therefore, the value of cosec A / cot A - sec A, using the given value of tan A = 4/3, is 1 + √(9/7)/3.
Learn more about cosec here
https://brainly.com/question/29479188
#SPJ11
Can someone help me I don't understand

Answers
Step-by-step explanation:
Hey there!
From the above right angled triangle ABC;
Taking Angle ABC as reference angle;
Angle ABC = ???
Perpendicular (p) = AC = 15
Base (b) = AB = 47
Now;
Taking ratio of sin;
\( \tan( \alpha ) = \frac{p}{b} \)
Keep value;
\( \tan( \alpha ) = \frac{15}{47} \)
Simplify it;
\( \tan( \alpha ) = 0.3191489\)
Take tan to next side;
Angle ABC (alpha) = tan'(0.3191489)
Therefore, the measure of angle ABC is 17.70°.
Hope it helps!

Help if your good at math I’ll mark brainliest:)
D.)10units sorry I couldn’t get it in the picture

Answers
Answer:
14
Step-by-step explanation:
-4,-5
2,3
-4-2= -6
-5-3= -8
-6+-8= 14
Answer:
the answer to this question is 10
Step-by-step explanation:
May i have brainliest
A park has a large circle painted in the middle of the playground area. The circle is divided into 444 equal sections, and each section is painted a different color. The radius of the circle is 10 \text{ meters}10 meters10, start text, space, m, e, t, e, r, s, end text. What is the area aaa of each section of the circle? give your answer in terms of pi.
Answers
The area of each section of the given circle of radius 10 meter is 25π sq. meter
What is circle?
A circle is a shut two-layered figure wherein the arrangement of the relative multitude of focuses in the plane is equidistant from a given point called "center". Each line that goes through the circle frames the line of reflection evenness. Additionally, it has rotational balance around the middle for each point.
According to question:there are 4 sections of the circle, radius of circle(r)=10 meter
We know that
Area of circle(A) = π(r)^2
A = π(10)^2
A = 100π sq. meter
Now the area of each section = area of circle/4
area of each section = 100π sq. meter/4 = 25π sq. meter
Thus, required area of section is 25π sq. meter.
To know more about circle visit:
brainly.com/question/12711347
#SPJ4
Jolene has 30 days to prepare for a
bicycle race. She will bicycle 15 miles
each day. How many miles will
Jolene have bicycled during her
training?

Answers
Answer:
450 miles in total during her training
Step-by-step explanation:
Since it does say she has 30 days to train and she said she will ride her bike 15 miles everyday she trains so she will have ridden her bike for 450 miles in total
30 days to train x 15 miles per day = 450 miles in total
can anyone help with this ??

Answers
Select the expression that is equivalent to 4x2 – 25.
Help
Answers
Answer:
Factor form: (2x-5)(2x+5)
If you olny simplify: 8x-25
Step-by-step explanation:
it is known that a certain kind of algae in the dead sea can double in population every 4 days. suppose that the population of algae grows exponentially, beginning now with a population of 3,000,000. (a) how long it will take for the population to quadruple in size? days (b) how long it will take for the population to triple in size? days
Answers
Since the algae grow exponentially with doubling time of 4 days, then the population will be quadruple in size in 8 days and will be triple in size in 6.34 days.
The easiest way is to consider the situation as a geometric sequence. If the population doubles its size in 4 days, then it will be quadruple in:
2 x 4 days = 8 days.
In general, we can use the growth formula:
P(t) = Po . 2^(t/Td)
Where:
P(t) = population at time t
Po = initial population
Td = doubling time
Parameters given:
Td = 4 days
P(t) = 3Po
Plug those parameters into the formula:
3 Po = Po . 2^(t/4)
3 = 2^(t/4)
log 3 = (t/4) log 2
t = 4 . log 3 / log 2 = 6.34 days.
Learn more about growth formula here:
https://brainly.com/question/27161222
#SPJ4
Which equation shows the commutative property of addition?

Answers
Answer:
the one that shows the commutative property of addition is
m + n = n + m
a group of 8 people are ordering pizza. Each person wants 3 slices and each pizza has 10 slices how many pizzas should they order
Answers
Answer:
3
Step-by-step explanation:
8 people
3 slices per person
8 × 3 = 24
They need 24 slices.
1 pizza has 10 slices.
24/10 = 2.4
They need 2.4 pizzas. Since they need to order a whole number of pizzas, they need to order 3 pizzas.
Answer: 3
use a graph and a table to solve the equation. round to the nearest thousandth if necessary x2 – 7x - 5 = 1/2x - 4
Answers
Answer:The nearest thousand is 6,0000Step-by-step explanation:
true or false. the x-intercept and the y-intercept for a line will never be the same ordered pair.
Answers
True, the x-intercept and the y-intercept will never be the same ordered pair because they have different x- and y-coordinates
Explanation:The statement is true. The x-intercept and the y-intercept for a line will never be the same ordered pair because they are two distinct points. The x-intercept is the point where a line crosses the x-axis, which means that the y-coordinate of this point is zero.
The y-intercept, on the other hand, is the point where the line crosses the y-axis, which means that the x-coordinate of this point is zero. Therefore, the x-intercept and the y-intercept will never be the same ordered pair because they have different x- and y-coordinates.
See more about intercept at: https://brainly.com/question/26233
#SPJ11
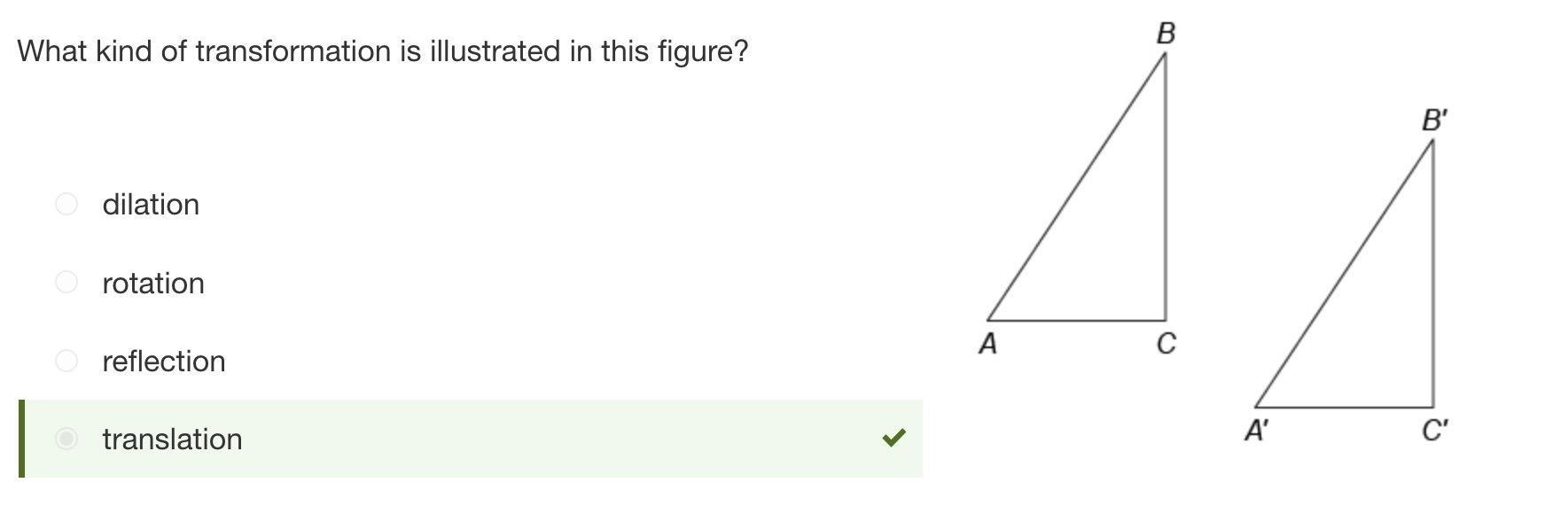
What kind of transformation is illustrated in this figure? Responses reflection reflection translation translation dilation dilation rotation rotation The image shows 2 congruent quadrilaterals A B C D and I J K L where A B C D is on the left side and quadrilateral I J K L is on the right side. An arrows is between the two figure indicating that A B C D slide over to be I J K L.
Answers
The transformation shown is Translation.
What is Geometric Transformation?Transformation of geometrical figures or points is the manipulation of a given figure to some other way.
Different types of transformations are Rotation, Reflection, Glide reflection, Translation and Dilation.
Given options are rotation, reflection, translation and dilation.
Rotation of a figure is when we rotate a figure about a certain degree.
So it is not rotation.
Reflection of a figure occurs when the figure is reflected over a line.
So it is not rotation.
Dilation is the enlarging or reduction of the size of figures.
So it is not dilation.
Translation of a figure is when we slide a figure in any direction.
Given transformation is translation.
Hence the transformation illustrated in the graph is translation.
Learn more about Geometric Transformation here :
https://brainly.com/question/10390366
#SPJ1
Diagram 2 is: Translation
yw^^

If two out of every fifteen trick or treaters that came to your house last halloween were dressed as spider-man, what proportion of trick or treaters were not dressed as spider-man?
Answers
Given:
The fraction of treaters dressed up us halloween, x=2/15.
Let the total trickers be taken as 1.
Now, the proportion of treakers that were not dressed up as spiderman is,
\(\begin{gathered} y=1-x \\ =1-\frac{2}{15} \\ =\frac{15-2}{15} \\ =\frac{13}{15} \end{gathered}\)Question 4 (3 points)
Timmy and Tommy are each earning money to go on a trip for school. In one weekend, Timmy earns a certain amount and tommy earns twice
what Timmy earned plus $24. Altogether, they earned $174.
How much did Timmy make?
Timmy made $
Answers
Answer:
$75
Step-by-step explanation:
let the amt. earned by timmy be x.
amt. earned by timmy=x
amt. earned by tommy=x +$24
therefore, x+x+$24=$174
or,2x +$24=$174
2x=$174-$24
2x=$150
x=$150/2
therefore, x or amt. earned by timmy=$75
Answer:
$75
Step-by-step explanation:
let the amt. earned by timmy be x.
amt. earned by timmy=x
amt. earned by tommy=x +$24
therefore, x+x+$24=$174
or,2x +$24=$174
2x=$174-$24
2x=$150
x=$150/2
therefore, x or amt. earned by timmy=$75
On Eduardo's workbench are the following
paint cans.
• 3 cans of red paint
• 5 cans of blue paint
• 8 cans of green paint
• 4 cans of yellow paint
Eduardo will randomly choose one can of
paint. What is the probability that he will
choose a can of red paint or a can of blue
paint? (71A, 7.1B, 7.1F)
Answers
Answer: 2/5
Step-by-step explanation:
Number of cans of red paint = 3
Number of cans of blue paint = 5
Number of cans of green paint = 8
Number of cans of yellow paint = 4
Total number of cans of paint = 20
The probability that Eduardo will
choose a can of red paint or a can of blue will be:
= P(red) + P(blue)
= 3/20 + 5/20
= 8/20
= 2/5
The probability is 2/5.
solve the equation
pic:

Answers
The solution to the equation \((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\) is 10.3891
How to solve the equationFrom the question, we have the following parameters that can be used in our computation:
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\)
Using the following trigonometry ratio
sin²(x) + cos²(x) = 1
We have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = (\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + 1 + e^2\)
The sum to infinity of a geometric series is
S = a/(1 - r)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = \frac{1/2}{1 - 1/2} + \frac{9/10}{1 - 1/10} + 1 + e^2\)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 1 + 1 + 1 + e^2\)
Evaluate the sum
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 3 + e^2\)
This gives
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 10.3891\)
Hence, the solution to the equation is 10.3891
Read more about summation notation at
brainly.com/question/15973233
#SPJ1
9.) Paul makes $300 a day and works 20 days a month, but he is fined $20 every day he is late. How
many days can he be late if he wants to make at least $5,910?
Answers
Answer:
3 days
Step-by-step explanation:
20 day x 300 dollar =6000 dollars
6000 dollar - 5910 dollar =90 dollar
Can be fined 80 dollar because 20 is even number
So,days can be fined:
60 dollar divide 20 dollar =3 days
olve the following differential equation by finding h and k so that the substitutions x equal suplush, y equal svplusk transform it into the homogeneous equation StartFraction dv Over du EndFraction equals StartFraction u minus v Over u plus v EndFraction dy/dx= (x-y-1)/(x+y+1)
Answers
We get: v - h + k - s = Ce^(-s/2) or y - x - (h - k) = Ce^(-(x-h-s)/2).
This is the general solution to the original differential equation, in terms of h, k, and C.
Homogeneous equation substitutionTo solve the differential equation
dy/dx = (x-y-1)/(x+y+1)
We can make the substitution x = h + s and y = v + k, where h and k are constants to be determined. This gives us:dy/dx = dv/ds + k
x - y - 1 = h + s - v - k - 1 = s - v + (h - k - 1)
x + y + 1 = h + s + v + k + 1 = s + v + (h + k + 1)
Substituting these into the differential equation and simplifying, we get:dv/ds + k = [(h + s - v - k - 1) - (s - v + (h - k - 1))] / [(h + s + v + k + 1) -
(s + v + (h + k + 1))]
Simplifying further, we get:dv/ds + k = [(2h - 2k - 2)s - 2v] / [-2]
or
dv/ds = (v - h + k - s) / 2
This is a homogeneous differential equation, which we can solve using the substitution u = v - h + k - s. Then,dv/ds = du/ds
and the equation becomes:
du/ds = -u/2
which has the general solution u = Ce^(-s/2). Substituting back, we get:v - h + k - s = Ce^(-s/2)
or
y - x - (h - k) = Ce^(-(x-h-s)/2)
This is the general solution to the original differential equation, in terms of h, k, and C.
Learn more about Homogeneous equation substitution here:
https://brainly.com/question/28170364
#SPJ4
Seven Friends divide three bags of apples equally between them. Enter the division represented by this situation as a fraction .
Answers
Answer:
7/3
Step-by-step explanation:
Specify the component functions of a vector field →F in R2 with the following property. →F is everywhere normal to the line x=2. Which of the following is one possible vector field →F ?
A. →F=(x,0)
B. →F=(−y,x)
C. →F=(x,y)
D. →F=(0,y)
Answers
Option D has a non-zero component function in the y-direction and a zero component function in the x-direction.
The vector field →F is normal to the line x=2, so it must be tangent to the line y-axis at every point. This means that the component function of →F in the x-direction should be 0 and the component function of →F in the y-direction should be non-zero.
Option D has a non-zero component function in the y-direction and a zero component function in the x-direction, so it satisfies the given property. Therefore, the answer is: D. →F=(0,y)
Learn more about y-direction here
https://brainly.com/question/14617282
#SPJ11
Pls help me ;-; I'm not very smart
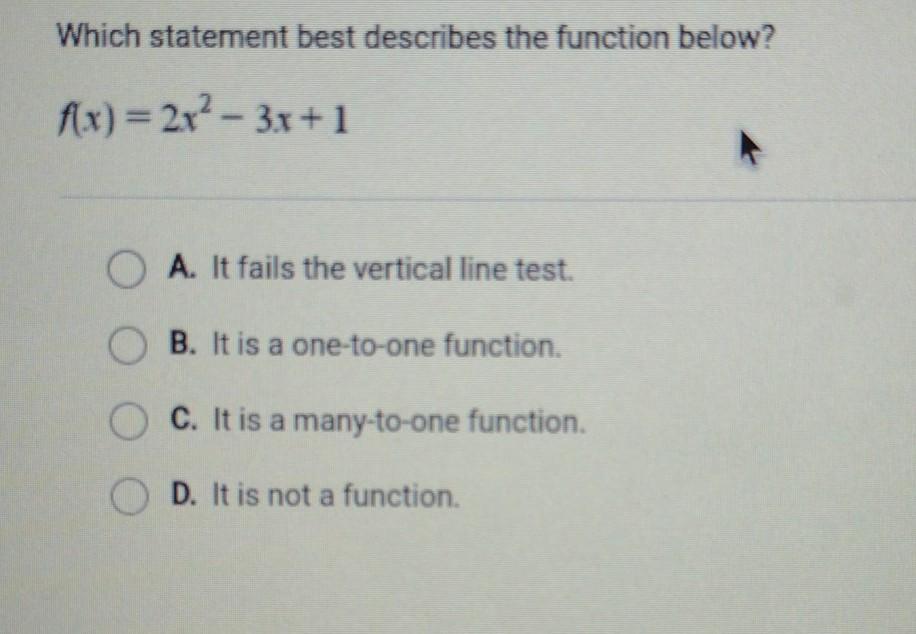
Answers
Answer:
It is one to one function
hope this will help you ☺️☺️
f(x)=2/3x^3-3/2x^2+x+C
Step-by-step explanation:
thus it's B
The flight of a cannonball toward a hill is described by the parabola y=2+0.12x- 0.0004x^2
Answers
The computation shows that the placw on the hill where the cannonball land is 3.75m.
How to illustrate the information?To find where on the hill the cannonball lands
So 0.15x = 2 + 0.12x - 0.002x²
Taking the LHS expression to the right and rearranging we have:
-0.002x² + 0.12x -.0.15x + 2 = 0.
So we have -0.002x²- 0.03x + 2 = 0
I'll multiply through by -1 so we have
0.002x² + 0.03x -2 = 0.
This is a quadratic equation with two solutions x1 = 25 and x2 = -40 since x cannot be negative x = 25.
The second solution y = 0.15 * 25 = 3.75
Learn more about computations on:
https://brainly.com/question/4658834
#SPJ4
Complete question:
The flight of a cannonball toward a hill is described by the parabola y = 2 + 0.12x - 0.002x 2 . the hill slopes upward along a path given by y = 0.15x. where on the hill does the cannonball land?
The coordinates of the midpoint of line GH are M(−132,−6) and the coordinates of one endpoint are G(−4, 1). The coordinates of the other endpoint are
Answers
Answer:
Since, the coordinates of the midpoint of line GH are M(\frac{-13}{2}, -6)(
2
−13
,−6) .
The coordinates of endpoint G are (-4,1)
We have to determine the coordinates of endpoint H.
The midpoint of the line segment joining the points (x_1, y_1)(x
1
,y
1
) and (x_2, y_2)(x
2
,y
2
) is given by the formula (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})(
2
x
1
+x
2
,
2
y
1
+y
2
) .
Here, The endpoint G is (-4,1) So, x_1 = -4 , y_1=1x
1
=−4,y
1
=1
Let the endpoint H be (x_2,y_2)(x
2
,y
2
)
The midpoint coordinate M is (\frac{-13}{2}, -6)(
2
−13
,−6) .
So, \frac{-13}{2} = \frac{-4+x_2}{2}
2
−13
=
2
−4+x
2
{-13} = {-4+x_2}−13=−4+x
2
{-13}+4 = {x_2}−13+4=x
2
{x_2}=9x
2
=9
Now, -6 = \frac{1+y_2}{2}−6=
2
1+y
2
-12 = {1+y_2}−12=1+y
2
y_2= -13y
2
=−13
So, the other endpoint H is (-9,-13).