Answers
Answer:
a = 64°
b = 138.7°
Step-by-step explanation:
First, Let's find the measure a,
180° = 116° + a180 - 116 = aa = 64°______
Now,
90° + a + 82° + x + x + x = 360°90+ 64 + 82 + 3x = 360° 236 + 3x = 360 3x = 124/ 3x = 41.3°______
Now that we found out what x equals, let's find 'b'-
b + x = 180°b + 41.3 = 180b = 180 - 41.3b = 138.7°Related Questions
The picture below shows Annie and her younger brother Tommy’s money.
They want to combine their money to buy something together. How much do they have in all?
Annie has 4 dollar bills, 11 dimes, and 4 pennies. Tommy has 3 times and 3 pennies.
Answers
Step-by-step explanation:
Annie: 4 dollars = $4 11 dimes = 11 x 0.10 = $1.1 ( since 1 dime = 0.10 dollars)
4 pennies =4 x 0.01= $0.04 ( since 1 penny = 0.01 dollars)
Tommy 3 dimes = 3 x 0.10 = $0.3 3 pennies = 3x 0.01 = $0.03
Adding the values: 4 +1.1+0.04+0.3+0.03 = $5.47
On a joint school visit, lan travels on his motor bike at an average speed of 24 km per
hour. Sarah travels in her car using the same route at an average speed of 5 meters per
second.
A) Who will arrive first?
(b) The journey time for Sarah is 20 mins. How far is the journey?
km
(c) How long did the journey take lan?
minutes
Answers
Answer:
A) Ian will arrive first.
B) 6 Kilometers
C) 15 Minutes
Step-by-step explanation:
In a math class of 32 students, 18 boys and 14 are girls. On a unit test, 5 boys and 7 girls made an A grade. A student is chosen at random from the class. What is the probability of choosing a girl or an A student?
Answers
Answer:
14+7=21
The probability is 21/32 or 65,625%
Step-by-step explanation:
You just add the number of girl students (including the ones that got an A) with the number of boys that got an A
Then you divide that number by the total of students (32)
The probability of choosing a girl or an A grade student is 19/32.
What is probability ?Probability is the chance or possibility to occur any selected event.
If the number of possible outcomes of an event is divided by the total number of outcomea of the event then it is called probability of that particular event.
What is the required probability ?In a maths class,
The total number of students = 32
No. of boys = 18 & no. of girls = 14
On an unit test, 5 boys made an A grade whereas 7 girls made an A grade.
The probability of choosing a girl = 14/32 = P(A) (say)
And, The probability of choosing an A grade student = 12/32 = P(B) (say)
Hence, the probability of choosing an A grade student who is a girl = P(A∩B) = 7/32
∴ The probability of choosing a girl or an A grade student =
P(A∪B) = P(A)+P(B)-P(A∩B)
= 14/32+ 12/32-7/32
= 26/32-7/32
= 19/32
Hence, The required probability is 19/32.
Learn more about probability here :
https://brainly.com/question/251701
#SPJ2
Brooklyn is going to invest in an account paying an interest rate of 3.5% compounded continuously. How much would Brooklyn need to invest, to the nearest ten dollars, for the value of the account to reach $64o in 9 years?
Answers
Brooklyn needs to invest $432.43, rounded to the nearest ten dollars.
To determine how much Brooklyn needs to invest in an account that pays a continuously compounded interest rate, we can use the formula:
A = \(Pe^(^r^t^)\)
where A is the future value of the account, P is the principal investment, e is the mathematical constant approximately equal to 2.71828, r is the interest rate, and t is the time in years.
In this case, we want the future value of the account to be $640, the interest rate is 3.5% (or 0.035 as a decimal), and the time is 9 years. We can substitute these values into the formula and solve for P:
640 = \(Pe^(^0^.^0^3^5^*^9^)\)
640 = Pe^0.315
P =\(640/e^0^.^3^1^5\)
P = 432.43
Therefore, to have a future value of $640 in 9 years with a continuously compounded interest rate of 3.5%.
For such more questions on invest
https://brainly.com/question/29227456
#SPJ8
Consider the polynomial
(4mn^2n - 2mn + 6) + (6mn^2 - 1) - (mn^2 - 2 + 9mn)
Combine all like terms and enter the coefficients for each term into the blanks below

Answers
(4mn^2n - 2mn + 6) + (6mn^2 - 1) - (mn^2 - 2 + 9mn)
First, let's remove the parentheses:
4mn^2 - 2mn + 6 + 6mn^2 - 1 - mn^2 + 2 - 9mn
Next, let's combine like terms by adding or subtracting coefficients of the same variables:
(4mn^2 + 6mn^2 - mn^2) + (-2mn - 9mn) + (6 + 2 - 1)
Simplifying further:
9mn^2 - 11mn + 7
So, the coefficients for each term are:
9, -11, 7
Christina’s savings account grows at a rate of 2% compounded quarterly. If her initial deposit is $750, write a function A(t)
that models the balance of the savings account after t years.
Answers
Answer:
Step-by-step explanation:
A = P * (1 + r/n)^(n*t
The function that gives the amount of money in dollars, J(t), in Jamie's account t years after the initial deposit is A = 750(1.0002)^4t. (in dollars)
How to calculate compound interest's amount?If the initial amount (also called as principal amount) is P, and the interest rate is R% per unit time, and it is left for T unit of time for that compound interest, then the interest amount earned is given by:
For this case, we're given that:
Initial amount Christina deposits = P = $750
Rate of interest = 2% compounding quarterly
Time = t years
Rate of interest is compounding quarterly.
Each year has 4 quarters.
Quarterly interest rate compounding quarterly = 2%.
t years has 4t quarters = T
Thus, we get the final amount in Christina’s account as
A = P * (1 + r/n)^(n*t)
A = 750(1 + 0.02/100)^4t
A = 750(1.0002)^4t
Thus, the function that gives the amount of money in dollars, J(t), in Christina’s account t years after the initial deposit is A = 750(1.0002)^4t (in dollars)
Learn more about compound interest here:
brainly.com/question/11897800
#SPJ1
Select ALL the correct answers.
For ΔABC, which two relationships are true?
An Image of a right-angle triangle BAC with B at the right angle. With an angle of (90 minus theta).
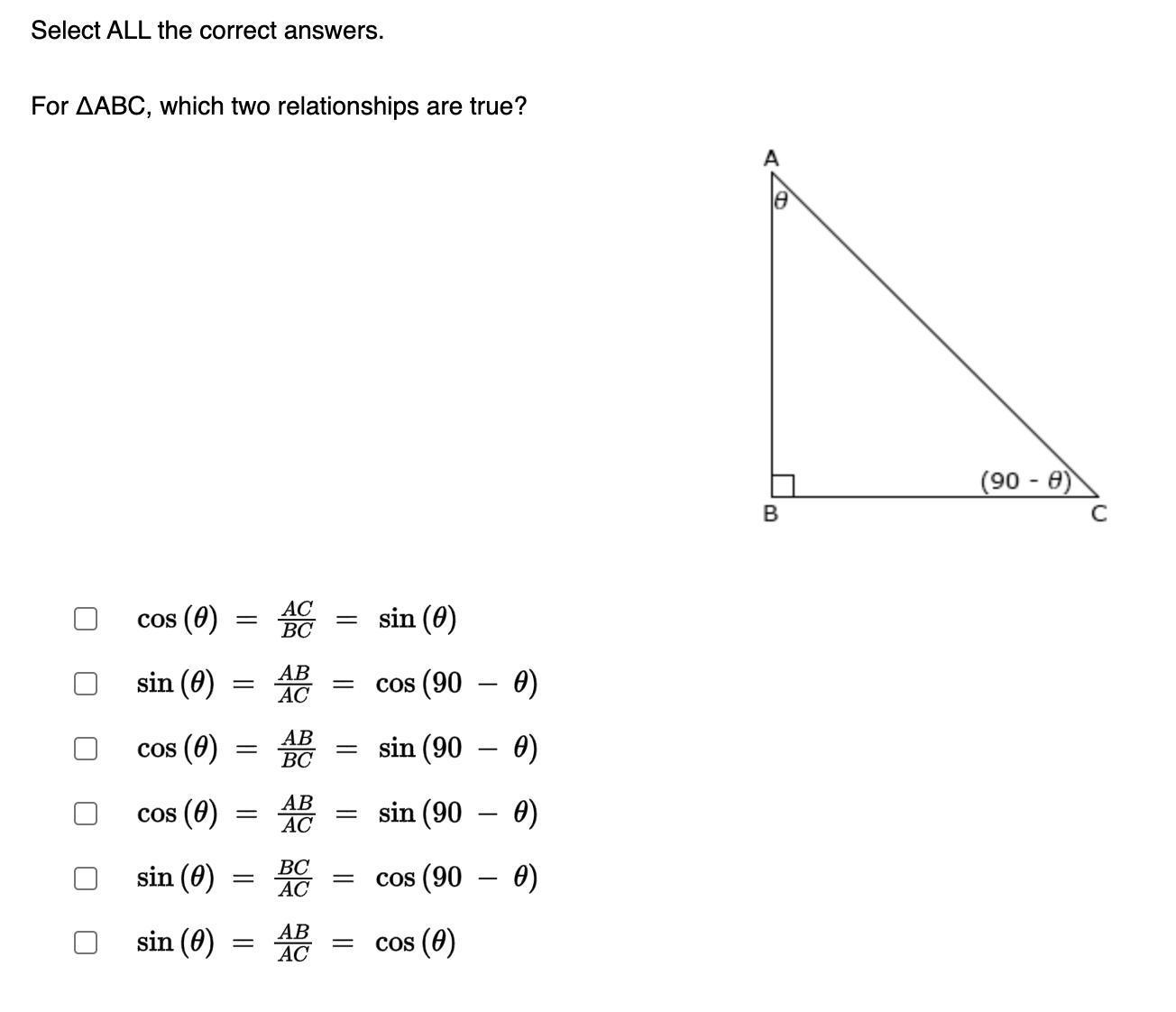
Answers
Answer:
Step-by-step explanation:
An Image of a right-angle triangle BAC with B at the right angle. With an angle of (90 minus theta).Refers to the attachment given below

What’s the correct answer for this question?

Answers
Answer:
The last option is the correct choice 33.5
Step-by-step explanation:
\(V=\pi r^2\frac{h}{3} \\=\pi 2^2\frac{8}{3} \\=33.51\\=33.5\)
Answer:
D
Step-by-step explanation:
In the attached file

Help help help help help

Answers
Answer:
Option 2: \(f^{(-1)}(x) = -\frac{3}{4x}\) is the correct answer.
Step-by-step explanation:
Given function is:
\(f(x) = -\frac{3}{4x}\)
There are few steps to find inverse of a function. We will apply them one by one onto the function
Step 1: Replacing f(x) with y
\(y = -\frac{3}{4x}\)
Step 2: Replacing y with x and x with y
\(x = -\frac{3}{4y}\)
Step 3: Solving the equation in step 2 for y
\(x = -\frac{3}{4y}\\y = -\frac{3}{4x}\)
Step 4: Replacing y with inverse of f
\(f^{(-1)}(x) = -\frac{3}{4x}\)
Hence,
Option 2: \(f^{(-1)}(x) = -\frac{3}{4x}\) is the correct answer.
After x hours of rainfall today, Yvette recorded the amount of rain in inches, y, in a rain gauge. The table shows the
linear relationship for the recorded rainfall.
Rain Gauge
Time, x (hours)
3 4 5
Amount of Rain in Gauge, y (inches) 3.75 4.5 5.25
How many inches of rain was in the gauge before the rain began today, and what was the rate at which the rain fell
in inches per hour?
A. There was 0 inches in the rain gauge before the rain began, and the rain fell at a rate of 1.25 inches per hour.
B. There was 2.5 inches in the rain gauge before the rain began, and the rain fell at a rate of 1.25 inches per hour.
C. There was 3 inches in the rain gauge before the rain began, and the rain fell at a rate of 0.75 inch per hour.
D. There was 1.5 inches in the rain gauge before the rain began, and the rain fell at a rate of 0.75 inch per hour.
Answers
The correct option is D, There was 1.5 inches in the rain gauge before the rain began, and the rain fell at a rate of 0.75 inch per hour.
How to write the linear equation?A general linear equation is written as:
y = ax + b
Where a is the slope and b is the y-intercept.
If a line passes through two points (x₁, y₁) and (x₂, y₂), then the slope is:
a = (y₂ - y₁)/(x₂ - x₁)
We can use the first two points:
a = (4.5 - 3.75)/(4 - 3)
a = 0.75
Then we can write:
y = 0.75x + b
replacing the values of the first point we will get:
3.75 = 0.75*3 + b
3.75 - 0.75*3 = b = 1.5
Then the rate is 0.75 and the initial amount is 1.5
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
If $a = 4$, $b = 2$, and $c = -5$, then what is the value of $\sqrt[3]{4a^4b^5} + \dfrac{a - c}{(b+c)^2}$?
Answer is not 13 or 31.
Answers
\(\sqrt[3]{4 a^4 b^5} = \sqrt[3]{4 \times 4^4 \times 2^5} = \sqrt[3]{(4\times 2)^5} = \sqrt[3]{(2^2\times2)^5} = \sqrt[3]{(2^3)^5} = \sqrt[3]{2^{15}} = \sqrt[3]{(2^5)^3} = 2^5 = 32\)
\(\dfrac{a-c}{(b+c)^2} = \dfrac{4-(-5)}{(2+(-5))^2} = \dfrac{4+5}{(2-5)^2} = \dfrac9{(-3)^2} = \dfrac99 = 1\)
Then the expression evaluates to 32 + 1 = 33.
The value of the expression
\($\sqrt[3]{4a^4b^5} + \dfrac{a - c}{(b+c)^2}$\)
is 33 when $a = 4$, $b = 2$, and $c = -5$.
How did we get the values?Let's substitute the given values into the expression and calculate the result:
Given:
$a = 4$
$b = 2$
$c = -5$
Substituting the values:
\($\sqrt[3]{4a^4b^5} + \dfrac{a - c}{(b+c)^2} = \sqrt[3]{4(4)^4(2)^5} + \dfrac{4 - (-5)}{(2+(-5))^2}$\)
Calculating the values within the cube root:
\($\sqrt[3]{4(4)^4(2)^5} = \sqrt[3]{4 \cdot 256 \cdot 32} = \sqrt[3]{32768} = 32$\)
Calculating the values within the fraction:
\($\dfrac{4 - (-5)}{(2+(-5))^2} = \dfrac{4 + 5}{(-3)^2} = \dfrac{9}{9} = 1$\)
Now we can substitute the calculated values back into the expression:
\($\sqrt[3]{4a^4b^5} + \dfrac{a - c}{(b+c)^2} = 32 + 1 = 33$\)
Therefore, the value of
\(\sqrt[3]{4a^4b^5} + \frac{a - c}{(b+c)^2} \: is \: 33 \: when \: a = 4, \: b = 2, and \: c = -5\)
learn more about cube root: https://brainly.com/question/24486461
#SPJ2
Solve the following equation for b. 1/2HB=d2
Answers
Steps to solve:
1/2hb = d²
~Divide 1/2h to both sides
b = 2d²/h
Best of Luck!
the formula of ONE INTERIOR ANGLE of a REGULAR polygon.
Answers
Answer:
180° - (360/n)°, where n is the number of sides of the polygon.
Step-by-step explanation:
Polygon has n sides.
Divide the polygon radially into n congruent, isosceles triangles.
For each triangle:
vertex angle = (360/n)°
sum of base angles = 180° - vertex angle = 180° - (360/n)°
Each interior angle of the n-gon = 180° - (360/n)°
Help I hope you can see both

Answers
Answer:
15 degrees for the first one
90 degrees for the second one
Step-by-step explanation:
A system of equations is shown below.
Equation A: 4x - y = -5
Equation B: x + 2y = 1
Which method eliminates one of the variables?
1.
Multiply equation A by 2 and add the result to equation B.
2.
Multiply equation B by 4 and add the result to equation A.
3.
Multiply equation A by 2 and equation B by 4, and add the results toge
4.
Multiply equation B by 2 and equation A by 4, and add the results toge
Answers
Answer:
this one has to be answer 1
Step-by-step explanation:
4x - y = -5
x + 2y =1
8x - 2y = -10
x + 2y = 1
9x = -9
Which statements are true about the angles in the diagram? Select three options. Angle ACE is supplementary to angle BCD. Angle BCE is supplementary to angle ACE. Angle BCD is supplementary to angle BCE. Angle ACE is congruent to angle BCE. Angle BCD is congruent to angle ACE.
Answers
Answer:
angle bce is supplementary to angle ace
angle bcd is supplementary to angle bce
angle bcd is congruent to angle ace
Step-by-step explanation:
I just took the test
Answer:angle bce is supplementary to angle ace
angle bcd is supplementary to angle bce
angle bcd is congruent to angle ace
Step-by-step explanation:
5. A length of rope is 20m long. If I cut it into 10 equal length pieces, how long is
each piece? *
what is given
Answers
20m / 10 = 2m
Each piece is 2m long.
Answer:
each piece is = 3 m long
Step-by-step explanation:
20 /10= 2
From the information given, (a) construct the indicated sample space and (b) answer the probability question.
a. A couple planning to have three children.
b. Find the probability of having exactly one girl.
Answers
Answer:
(a) 3 (b) 1/3
Step-by-step explanation:
The probability is defined as the ratio of number of elements in event to the number of elements in sample space.
(a) As the total number of child is 3, so the number of elements in sample space = 3
(b) The sample space is { boy, boy, girl}
So, the probability is 1/3.
Thank you everybody in advance for your kind attention and cooperation!
Seats for Sale
State's football program has risen to the ranks of the elite with postseason bowl games in each of the past 10 years, including a national championship game. The Bruins (as the fans are called) fill the stadium each game. Season tickets are increasingly difficult to find. In response to the outstanding fan support, State has decided to use its bowl revenues to expand the stadium to 75,000 seats.
The administration is confident that all 75,000 seats can be sold at the normal price of $40 per game ticket; however, Frank Pinto's job, as athletic director, is to get as much revenue out of the stadium expansion as possible. In addition to stadium boxes for wealthy alums, Frank would like to take this opportunity to repurpose existing seats. A certain number of seats (yet to be determined) would be set aside for premium ticket holders who would pay $200 per ticket for the privilege of 50-yard line seats with chair backs and access to indoor concessions. The question is, how many fans would be willing to pay such a premium? If too many seats are designated in the premium sections, they could remain vacant. Too few premium seats would lose potential revenue for the program.
Frank has decided that if the plan has any chance of success, unsold premium seats should not be sold at reduced rates. It would be better to donate them to local charities instead. Gathering data from his cohorts at peer institutions, Frank has put together the following probability distribution of premium ticket holders. The data begin with 1000 tickets since Frank already has requests for 999 tickets from alumni donors. He is asking for your help in performing the analysis.
No. of Premium Tickets Probability
1,000 0.10
5,000 0.30
10,000 0.24
15,000 0.15
20,000 0.10
25,000 0.06
30,000 0.05
a. Using revenue management, determine how many seats should be reserved for premium ticket holders.
b. Considering your answer to part (a) and the possible outcomes listed above, how much total revenue (i.e., regular and premium) can be expected from ticket sales?
c. The administration is unsure about Frank's plan. The VP of finance thinks an expected value of the number of premium seats would produce better results. How would the number of premium seats change using expected value? Considering the possible outcomes, which approach yields the most potential revenue?
Answers
Answer:
b. Considering your answer to part (a) and the possible outcomes listed above, how much total revenue (i.e., regular and premium) can be expected from ticket sales?
Jonathan has 30 chocolates. He gives some chocolates to his friend David. He then gives Sarah half the number of chocolates that he gave David and gives Lily two-thirds of what he gave David. After giving away the chocolates, Jonathan has 4 chocolates left. If the number of chocolates Jonathan gives David is x, which equation represents the situation? How many solutions does this equation have?
Answers
Answer:
equation which represent this situation is 30 - 13x/6 =4
Solution to this equation is x = 12
As we see that there is one equation and degree of x is one thus there is one solution.
Step-by-step explanation:
Total no. of chocolates with Jonathan = 30
no. of chocolates given to David IS x
Given
He then gives Sarah half the number of chocolates that he gave David
no. of chocolates given to Sarah = 1/2 of no. of chocolates given to David
no. of chocolates given to Sarah = 1/2 of x = x/2
Again given
gives Lily two-thirds of what he gave David. After giving away the chocolates
no. of chocolates given to Lily = 2/3 of no. of chocolates given to David
no. of chocolates given to Lily = 2/3 of x = 2x/3
Total no. of chocolates given to David , Sarah and lily = x+x/2+2x/3
LCM of 2 and 3 is 6
Total no. of chocolates given to David , Sarah and lily =( 6x + 3x+ 4x)/6
Total no. of chocolates given to David , Sarah and lily =13x/6
Now, additional information in the problem is
After giving away the chocolates, Jonathan has 4 chocolates left
Chocolate left with Jonathan = Total no. of chocolates with Jonathan - Total no. of chocolates given to David , Sarah and lily
4 = 30 - 13x/6
=> 4 + 13x/6 = 30
=> 13x/6 = 30-4 = 26
=> x = 26*6/13 = 2*6 =12
Thus, equation which represent this situation is 30 - 13x/6 =4
Solution to this equation is x = 12
As we see that there is one equation and degree of x is one thus there is one solution.
The best approximation for square root of 10 Is
25
03.1
05
100
Answers
If △ EFG ∼ △ ABC
, What value of x will make the two triangles similar?

Answers
Answer:
the value of x will be 9 they all are similar so we will just take ratios and do cross multiplication
HELP JIMTHOMPSON5910

Answers
Answers:
Answer for problem 12) Approximately 200.96 square inchesAnswer for problem 13) Approximately 150.72 inchesEach approximate value used pi = 3.14
=====================================================
Explanations:
Problem 12
The larger circle has a diameter of 48 inches. Each smaller circle has a diameter of 48/3 = 16 inches because we have three identical smaller circles stacked on top of each other to exactly the height or diameter of the larger circle.
That 16 inch diameter cuts in half to 8 inches, which is the radius of any given smaller circle. We'll plug r = 8 into the area formula below to get the following result:
A = pi*r^2
A = 3.14*8^2
A = 200.96
This is the approximate area of one smaller circle. The value is approximate because pi = 3.14 is approximate. To get a more accurate answer, use more decimal digits of pi.
The units for the area are in "square inches" which we can write as "square in" or as "in^2".
-----------------------------------------
Problem 13
The diameter is d = 48 which is plugged into the circumference formula below
C = pi*d
C = 3.14*48
C = 150.72
The perimeter of the larger circle is roughly 150.72 inches
The circumference is the perimeter of the circle, i.e. the distance around the circle's edge.
9(7/4)-2= what in fraction form ? Can someone please help ?
Answers
Answer:
55/4
Step-by-step explanation:
Which value of a would make the expression 5
13÷4a
equivalent to a whole number?
5
7
9
11
Answers
A value of a that would make the expression 5 1/3 ÷ 4/a equivalent to a whole number include the following: C. 9.
How to determine the value of that would make the expression equivalent to a whole number?In order to use the given expressions to determine the value of a (a-value) that makes the expression equivalent to a whole number, we would have to substitute the values of a (a-value or domain) into each of the expressions and then evaluate as follows;
First of all, we would re-write the mixed fraction as an improper fraction and then evaluate the given expression;
16/3 ÷ 4/a
16/3 × a/4
When a = 5, we have the following:
16/3 × a/4
16/3 × 5/4 = 20/3 (not a whole number).
When a = 7, we have the following:
16/3 × a/4
16/3 × 7/4 = 28/3 (not a whole number).
When a = 5, we have the following:
16/3 × a/4
16/3 × 9/4 = 36/3
36/3 = 12 (a whole number).
When a = 11, we have the following:
16/3 × a/4
16/3 × 11/4 = 44/3 (not a whole number).
Read more on expressions and whole number here: https://brainly.com/question/18864049
#SPJ1
Complete Question:
Which value of a would make the expression 5 1/3 ÷ 4/a equivalent to a whole number?
5
7
9
11
Which expression could be used to find any term in the following pattern?
1,8, 27, 64, ...
Select one:
a. 3x
b. 4x
C. x^2
d. x^3
pls answer :)
Answers
Answer:
MATH. I'm sorry
Step-by-step explanation:
3. An arithmetic sequence a begins 11, 7,...
a. Write a recursive definition for this sequence using function notatio
b. Sketch a graph of the first 5 terms of a
Answers
We get the function notation as aₙ = 15 - 4 n for the arithmetic sequence beginning with 11, 7,...
We are given an arithmetic sequence:
11, 7, …
We get from the sequence that:
a = 11 ( initial term )
d = 7 - 11 = - 4 ( common difference )
Now the nth term will be given as:
aₙ = a + (n - 1) d
aₙ = 11 + (n - 1) ( - 4 )
aₙ = 11 - 4 n + 4
aₙ = 15 - 4 n
Third term = 7 - 4 = 3
Fourth term = 3 - 4 = - 1
Fifth term = - 1 - 4 = - 5
Therefore, we get the function notation as aₙ = 15 - 4 n for the arithmetic sequence beginning with 11, 7,...
Learn more about arithmetic sequence here:
https://brainly.com/question/6561461
#SPJ9

Find the value of x in the figure below.
Write an equation and solve for x.
Choose the best answer.
x = 35
x = - 35
x = 33.5

Answers
Answer:
x=33.5
Step-by-step explanation:Sorry I only know the answer
Renee is designing a logo for an airline. She starts by making a figure with angle measures as shown. She
measures AB and finds that the length of the segment is 5 inches. Can she determine the length of DB
without measuring? Complete the explanation of how she can or cannot.
А
17°
B
110°
110°
C С
17°
D
AABC (select) ADBC by the (select) Triangle Congruence Theorem AB and D8 are
corresponding parts, and corresponding parts of congruent triangles are congruent, so she can conclude
that DB
inches

Answers
Hi :) I was wondering if you could help, I'm mixed up about this one.

Answers
Answer:
the image is sideways
Step-by-step explanation:
Answer:
well buddy see you thinking to hard its right there just relax and look closely
Step-by-step explanation:
