Fill in the blanks to make the statement true.
Pi the ratio of the (choose your answer...) of a circle to its ( choose your answer....)
Answers
Pi is the ratio of the circumference of a circle to its diameter.
Related Questions
LetVbe the vector space of continuous functions defined on the interval[0,1]. Define an inner product onVby the following rule:⟨f,g⟩=∫01f(x)g(x)dx.Use the Gram-Schmidt orthonormalization procedure to produce an orthonormal basis for the subspace spanned by1,x,x2. Use the results to find the closest-point projection ofx3into this subspace.
Answers
The closest projection will have a value of -29/360.
we will follow these steps to use the Gram-Schmidt orthonormalization procedure for producing an orthonormal basis for the subspace spanned by 1, x, and x²,
Set u₁ = 1, a unit vector.
Set v₂ = x and u₂ = v₂ / ||v₂||.
Set v₃ = x² - (x², u₁)u₁ - (x², u₂)u₂, and u₃ = v₃ / ||v₃||.
Thus we get the orthonormal basis for the subspace spanned by 1, x, and x² to be {u₁, u₂, u₃}.
Now we will use the formula for the projection of a vector onto a subspace to find the closest-point projection of x³ into this subspace,
proj_subspace(x³) = (x³, u₁)u₁ + (x³, u₂)u₂ + (x³, u₃)u₃
The inner products will be calculated as follows:
(x³, u₁) = ∫x³ X 1 dx = 1/4
(x³, u₂) = ∫ x³ X x dx = 1/5
(x³, u₃) = ∫ x³ * (x² - (x², u₁)u₁ - (x², u₂)u₂) dx
Here all the integrals will have limits of 0 and 1.
Hence we get
= 1/9 - 1/4 X 1/2 - 1/5 X 1/3
= 1/9 - 1/8 - 1/15
= (40 - 45 - 24)/360
= -29/360
Thus, the projection of x³ onto the subspace spanned by 1, x, and x² is:
proj_subspace(x³) = 1/4 X u₁ + 1/5 X u₂ + (1/9 - 1/4 X 1/2 - 1/5 X 1/3) X u₃
This projection is the closest point in the subspace to x³, in the sense that the distance between x³ and proj_subspace(x³) is minimized.
To know more about Gram-Schmidt orthonormalization visit
https://brainly.com/question/16034815
#SPJ4
PLEASE SHOW HOW YOU GOT THE ANSWER THANKS!
GIVING BRAINLIEST!!!

Answers
Answer:
a) 5 b) 1 c) 0 d) -4
Explanation:
a) 10[(1/2+1/4) + 2(1/8)] ÷ 2
Ok, there's a lot going on. You will want to follow PEMDAS, the acronym of the Order of Operations. It stands for Parentheses, Exponents, Multiplication/Division, and Addition/Subtraction. The M/D can be switched depending on what comes first from left to right, and same goes for A/S.
First, start off by doing everything in the brackets.
Let's add 1/2 and 1/4. To add fractions, they have to have a common denominator. I'm making 1/2 into 2/4 but multiplying the top and bottom by 2. Now it is 2/4 + 1/4 so we can add to get 3/4.
The other thing inside the brackets is 2(1/8). We can just multiply straight across and get 2/8. This can be simplified to 1/4.
Now, we add 3/4 and 1/4. The denominators are already the same, so we can just add them together to get 4/4 or 1.
Rewriting the equation, we now have 10(1)÷2
10•1 = 10
10 ÷ 2 = 5
The answer to question a is 5.
b) √(0.6)² + (0.8)²
First, we need to square both terms. Squaring is the same as multiplying the number by itself.
0.6 • 0.6 = 0.36
0.8 • 0.8 = 0.64
Add them together: 0.36 + 0.64 = 1
√1 = 1
The answer to question b is 1.
c) (1/5 - 3/5) • √6•3/2 + (√36 ÷ √5²)
Let's start with the first bit: (1/5 - 3/5)
The denominators are the same, so just subtract and you get -2/5
The second bit now: \(\sqrt{6 *\frac{3}{2} }\)
Multiply across and you get 18/2, which can be simplified to 9
√9 = 3
The third section: (\(\sqrt{36}\)÷ \(\sqrt{5^{2} }\))
The square root of 36 = 6 (because 6•6=36, so it's right)
The square root and the square cancel each other out, so the second part is 5.
6 ÷ 5 = 1.2
Now put it all together: -2/5 • 3 + 1.2
I'm making the 1.2 into a fraction so it is the same as the fraction: 1.2 = 6/5
We now have -2/5 • 3 + 6/5
First we multiply -2/5 and 3 across:
-2/5 • 3 = -6/5
Now we add -6/5 and 6/5 across:
-6/5 + 6/5 = 0
d) [-1.5 + √0.25 - (-0.75)] • 2^4
Doing the brackets first:
The square root of 0.25 = 0.5 (because 0.5 • 0.5 = 0.25)
-1.5 + 0.5 - -0.75
-1 + 0.75 (subtracting a negative make a positive)
-0.25
-0.25 • 2^4
2^4 = 16 (this is saying 2•2•2•2 which is 16)
-.25 • 16 = -4
What is the solution to the system of equations?
OA. (1,4)
OB. (4,1)
OC. (4, -1)
OD. (-1,4)

Answers
Answer:
a(1,4)
Step-by-step explanation:
This is the point where the two lines meet. When x = 1 and y = 4
(1,4)
What is the area of the drawing of the trophy shown?

Answers
Answer:
The area of the drawing is 12 Squares
PLS HELP ASAP WILL GIVE YOU BRAINLIEST
Which of the equations below represents a line parallel to the x-axis?
o
A.
5
B.
11
C.
y
T
OD
Y
= 5
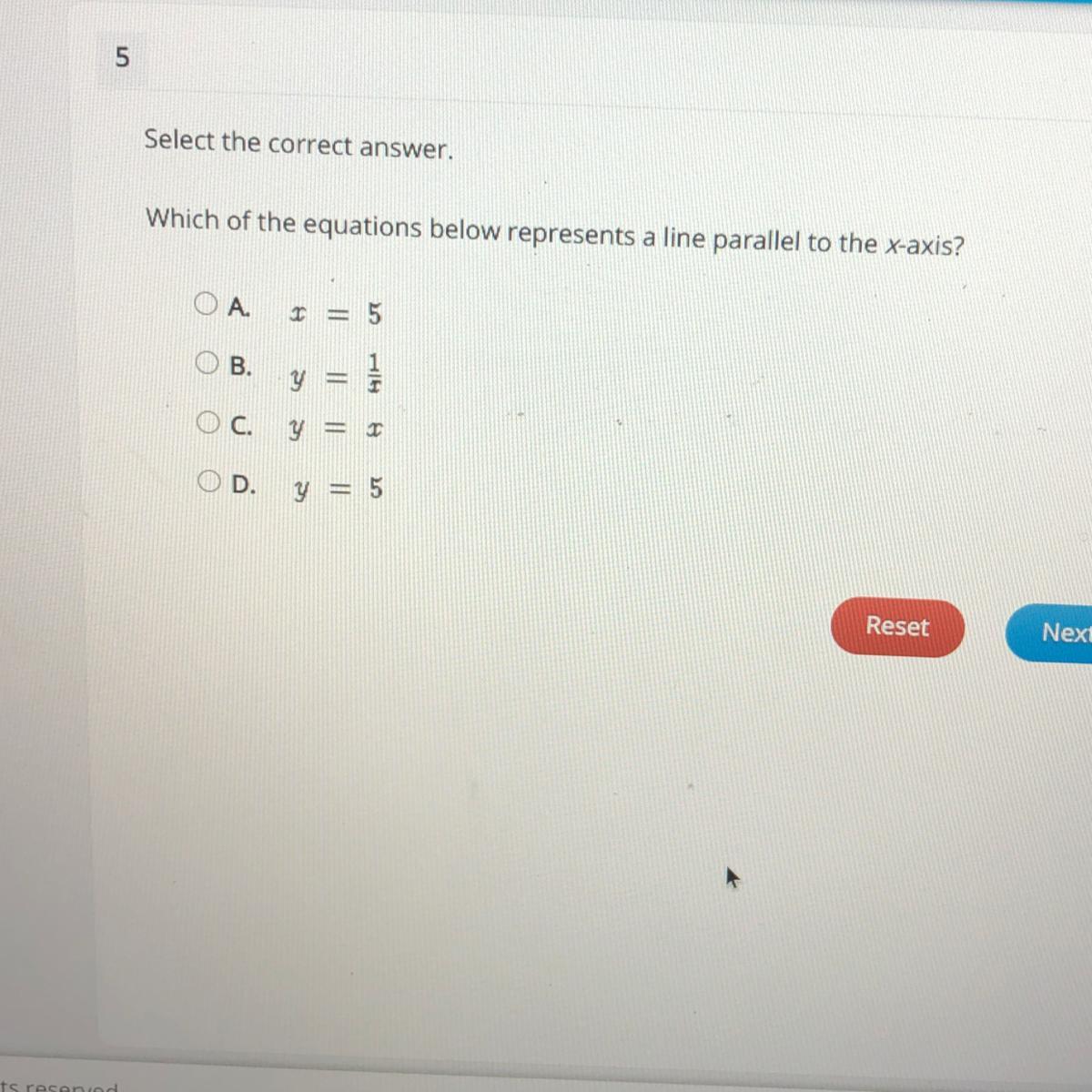
Answers
Answer:
y=5 is the correct answer
Step-by-step explanation:
it would be paralell because the x variable goes across in a straight line
Answer:
A) x=5
Step-by-step explanation:
I would recommend using desmos as well :)
An electrician has the following lengths of cable:
21 inches, 39 inches, and 8 feet.
How much cable does he have in feet?
Answers
Answer:
13 feet of cable
Step-by-step explanation:
Convert 8 ft to inches (96 in)
96+39+21= 156
156/12= 13
In AOPQ, the measure of angle Q=90°, the measure of angle O=66°, and QO = 4.5 feet. Find the length of OP to the nearest tenth of a fo
Answers
Answer:11.1 feet
Step-by-step explanation:
7. A floor is covered by 800 tiles measuring 10 squared cm. How many square tiles of side 8 cm would be needed to cover the same floor?
Answers
Answer:
1000 tiles
Step-by-step explanation:
Determine total floor space
800 x 10 = 8000 squared cm total floor space.
Divide floor space by size of tile
8000 / 8 = 1000 tiles now required to cover the floor.
help help help........

Answers
Answer: D
Step-by-step explanation:
Range affects y-coordinates
Range starts from -8 and ends at 7. -8 is included in the range, but 7 isn't.
Hence, the answer is -8<=y<7, but the best matching answer is -8<=y<8 since these two inequalities share the most number of solutions.
Hence, the answer is D
The instructor noted the following scores on the last quiz of the semester for 8 students. Find the range of this data set 59,61,83,67,81,80,81,100
Answers
answer: the range is 41.
to find the range of this data set, we first need to find the minimum and maximum values - which are 59 and 100.
then we subtract the minimum from the maximum.
59 - 100 = 41.
What is the value of this expression?
8-4x3^3+11
Answers:
119
23
-89
-17
Answers
\(8 - 4( {3}^{3} ) + 11 \\ 8 - 4(27) + 11 \\ 8 - 108 + 11 \\ 8 - 97 \\ - 89\)
Solve the puzzle and add the colors

Answers
Answer:
43
Step-by-step explanation:
Green: 9 - 2(-3) = 9 + 6 = 15
Red: -2(-3) + 4 = 6 + 4 = 10
Dark blue: 7x + 5 = 19
7x = 19 - 5 = 14
x = 14/7 = 2
Light blue: 6x + 3 = 21
6x = 21 - 3 = 18
x = 18/6 = 3
Red(Lt blue) - Dk blue + Green = 10(3) - 2 + 15 = 43
about how many times large is 7.9x10^4 than 2.1x10^3
Answers
3.76 many times large is 7.9 x 10⁴ than 2.1 x 10³. This can be solved using scientific notation method.
What is scientific notation?A method of writing numbers that combines a power of 10 with a number between 1 and 10. Using scientific notation, one may express extremely big or extremely small values. Once a number between 1 and 10 has been multiplied by such a power of 10, it is then expressed in scientific notation. For instance, 6.9 × 10⁸ can be used to represent the number 690,000,000.
The main goal of scientific notation is to simplify computations using numbers that are abnormally big or tiny. When a number is written in scientific notation, all of the digits are important since zeros are no longer utilized to set the decimal point.
For: 7.9 x 10⁴
= (79/10) x 10⁴
= 79 x 10³
on the other hand for: 2.1 x 10³
Thus, 3.76 many times large is 7.9 x 10⁴ than 2.1 x 10³.
To know more about scientific notation refer to:
https://brainly.com/question/1767229
#SPJ1
Shane spent 25% less buying her English reading book than Carissa. John spent 8% less than Carissa. John spent more than Shane by what percent?
Answers
Answer:
17%
Step-by-step explanation:
Let's say Carissa spent $100 on her English reading book. Shane spent 25% less, so she spent $75. John spent 8% less than Carissa, so he spent $92. John spent $17 more than Shane, so the answer is 17%
help help help help

Answers
Answer:
1372 cm^3
Step-by-step explanation:
\(\frac{4}{3} (3)(7^3)=\frac{4}{3} (3)(343)=\frac{4}{3} (1029)=1372\)
The estimated population is 1242 and the actual population is 1378.
The percent error is approximately
Answers
The percentage error is approximately 10%
How to estimate the percent error?We have:
Estimated = 1242
Actual = 1378
The change in the measurement is:
Change = Actual - Estimate
So, we have:
Change = 1378 - 1242
Evaluate
Change = 136
The percentage error is then calculated as:
Percentage error = Change * 100%/Actual
This gives
Percentage error = 136 * 100%/1378
Evaluate
Percentage error = 9.869%
Approximate
Percentage error = 10%
Hence, the percentage error is approximately 10%
Read more about percentage error at:
https://brainly.com/question/10892002
#SPJ9
Which equation represents the graphed function?

Answers
The linear function graphed is defined as follows:
y = 3x/2 - 3.
(third option).
What is a linear function?The slope-intercept definition of a linear function is given as follows:
y = mx + b.
In which:
The slope m represents the rate of change.The intercept b represents the value of y when the graph crosses the y-axis.The graph crosses the y-axis at y = -3, hence the intercept b is given as follows:
b = -3.
When x increases by 2, y increases by 3, hence the slope m is given as follows:
m = 3/2.
Then the function is defined as follows:
y = 3x/2 - 3.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Find the magnitude and direction of the vector using the given information. V=<6,7>

Answers
Answer:
The magnitude of the vector is 9.165 and it's direction is 40.6°
Step-by-step explanation:
Vector Quantities:A vector quantity is a quantity that has both size (magnitude) and direction. Examples of vector quantities are force, velocity and impulse.
Magnitude of vector v is given by
|v| = √6²+7²
= √36+49
= √84
= 9.165
Direction of vector v is obtained by:
\( \tan( \theta) = \frac{x}{y} \)
\(\theta = {tan}^{ - 1} ( \frac{6}{7}) \)
\(\theta = {40.6°}\)
Learn more about vector quantities from: https://brainly.in/question/3437975
#SPJ1
Find the area of the triangle
3 m
8 m
Answers
area - 1/2 x 3 x 8
Answer:
3×8 =24
24÷2=12
Area of triangle=12m²
Step-by-step explanation:
3×8 =24
24÷2=12
find the value of each expression when z=1,when z=2 and when z =3. then identify which expression are equivalent. 9z - 4-3z and 2(3z-2) and 9z-4z-3
Answers
Answer: the answer is :z^3+5z-7
Step-by-step explanation:
Find Matrix mixed questions

Answers
The only matrix that is certainly symmetric is a)\((a^2 - b^2).\)
We know that a matrix A is symmetric if it is equal to its transpose, that is \(A = A^T.\)
a) \((a^2 - b^2)\)
We can write the transpose of this matrix as
\((a^2 - b^2)^T = (a^2)^T - (b^2)^T = a^2 - b^2\), which is equal to the original matrix. Therefore, this matrix is symmetric.
b) (A+B)(A-B)
Expanding this expression, we get \((A+B)(A-B) = A^2 - AB + BA - B^2.\)
Taking the transpose of this, we get \((A^2)^T - (AB)^T + (BA)^T - (B^2)^T = A^2 - BA + AB - B^2.\)
Since AB and BA may not be equal, we cannot say for certain that this matrix is symmetric.
c) ABA
Taking the transpose of this matrix, we get\((ABA)^T = A^T B^T A^T\). Since \(A^T and B^T\) may not commute, we cannot say for certain that this matrix is symmetric.
d) ABAB
Taking the transpose of this matrix, we get \((ABAB)^T = B^T A^T B^T A^T\). Again, since \(A^T and B^T\) may not commute, we cannot say for certain that this matrix is symmetric.
Therefore, the only matrix that is certainly symmetric is a) \((a^2 - b^2).\)
for such more question on matrix
https://brainly.com/question/25581637
#SPJ11
CO
A charity bingo game costs $2 per round and has a $13 entry fee for an adult. It costs $3 per round and a $10 entry
fee for a child. For how many rounds of bingo are the costs the same for an adult and a child?
02
3
4
5
Nex
Save and Exit
Subm
Mark this and return
Answers
Answer:
3 rounds of bingo
Step-by-step explanation:
Let x represent the number of bingo rounds
For adults, the total cost can be represented by 2x + 13, since it is $2 per game and there is a $13 entry fee
For children, the cost can be represented by 3x + 10, since it is $3 per round and there is a $10 entry fee
To find how many rounds are needed to make the cost the same, set these expressions equal to each other and solve for x:
2x + 13 = 3x + 10
13 = x + 10
3 = x
So, costs will be the same with 3 rounds of bingo
Find the value of x in the parallelogram

Answers
The value of x in the parallelogram is 112°.
In a parallelogram, adjacent angles are always supplementary. This means that the sum of two adjacent angles in a parallelogram is always 180 degrees.
To understand this concept, let's consider a parallelogram ABCD. The opposite sides of a parallelogram are parallel and equal in length, and the opposite angles are congruent. Adjacent angles are those that share a side. Let's say angle A and angle B are adjacent angles in the parallelogram.
Since opposite angles of a parallelogram are congruent, we have angle A is congruent to angle C, and angle B is congruent to angle D.
Now, let's consider angle A and angle B. The sum of angle A and angle B is equal to the sum of angle C and angle D because opposite angles are congruent.
Therefore, we can conclude that angle A + angle B = angle C + angle D = 180 degrees.
This property holds true for all parallelograms. So, in any parallelogram, the adjacent angles are always supplementary, meaning their sum is 180 degrees.
For the given question, we know x° + 68° = 180°.
Then x° = 180° - 68°
x° = 112°
For more such questions on parallelogram
https://brainly.com/question/20526916
#SPJ8
A relation R on a set A is defined to be irreflexive if, and only if, for every x ∈ A, x R x; asymmetric if, and only if, for every x, y ∈ A if x R y then y R x; intransitive if, and only if, for every x, y, z ∈ A, if x R y and y R z then x R z. Let A = {0, 1, 2, 3}, and define a relation R2 on A as follows. R2 = (0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (2, 3) Is R2 irreflexive, asymmetric, intransitive, or none of these? (Select all that apply.) R2 is irreflexive. R2 is asymmetric. R2 is intransitive. R2 is neither irreflexive, asymmetric, nor intransitive.
Answers
Answer:
OMG IM ON THE SAME QUESTION
Step-by-step explanation:
Distributive property, i think the answer is either (A) or (B).

Answers
SOLUTION
From Distributive property, we have that
\(a(b+c)=a(b)+a(c)\)So apply this to the question, we have that
\(9(5\frac{2}{3})\)Becomes
\(\begin{gathered} 9(5\frac{2}{3})= \\ 9(5)+9(\frac{2}{3}) \end{gathered}\)Hence the answer is option B
A sales person starts working 40 hours per week at a job with 2 options for being paid . Option A is an hourly wage of $19. Option B is a commission rate of 8% on weekly sales.
How much does the sales person need to sell in a given week to earn the same amount with each option?
A. $9,500
B. $4,750
C. $760
D. $320
Answers
Given, Option A: Hourly wage is $19 and the salesperson works 40 hours per week. So, he will earn in a week \(\sf = 19 \times 40 = \$760\)
Now, according to option b, he will get 8% commission on weekly sales.
Let. x = the amount of weekly sales.
To earn the same amount of option A, he will have to equal the 8% of x to $760
So, \(\sf \dfrac{8x}{100}=760\)
Or, \(\sf 8x= 76000\)
Or, \(\sf x= \dfrac{76000}{8}=9500\)
the salesman needs to make a weekly sales of $9,500 to earn the same amount with two options.
Use the graph below to find the following:
A) what is the slope of the line?
B) what is the y intercept of the line?
C) what is the equation of the line in slope intercept form?

Answers
B.) The y-intercept is b=-5
C.) The equation is: y=-2x-5
f a vector coincides with its orthogonal projection onto a subspace, then the vector must be in the subspace.
Answers
The Orthogonal projection of A on Z i.e subspace formed by X and Y is A cos (90- θ) = A sin (θ).
A figure projected in parallel rays. In this projection, tangencies are preserved. On parallel lines, parallel lines converge. Both the length-to-area ratio and the length-to-area ratio of parallel segments are maintained. Any triangle can be positioned so that an orthogonal projection results in an equilateral shadow.
Let's say we have a vector. A and vector X and Y
Consider the subspace that is vector-formed. X and Y are perpendicular to the subspace vector Z, where Z = X + Y.
Cos = (X * Y) can be used to calculate the angle between X * Y and A.
A/|(X * Y)| * |A|
Now, Z and A are at a 90° angle.
As a result, A's projection onto Z, or the subspace created by X and Y, is given by A cos (90 - ) = A sin ().
The angle between the subspace and the vector whose projection we are trying to find must be determined in order to find the projection.
Use MATLAB Code for locating a projection on vector a on the subspace defined by vectors x and y. so that it will be more easy to understand
% cross product of x and y vector
xCrossY = cross(x, y);
% angle between xCrossY and vector 'a'
angle_radian = dot(xCrossY,a)/(norm(xCrossY)*norm(a));
% angle in degrees
angle_deg = rad2deg(angle_radian);
% projection of a on subspace made by x and y is asin(angle_deg)
projection = norm(a)*sin(angle_deg);
A cos (90- ) = A sin () is the orthogonal projection of A on Z, i.e. the subspace created by X and Y.
To learn more about Orthogonal projection visit:
brainly.com/question/2292926
#SPJ4
5. A baker had 2 pans of corn bread. He served 1 1/4 pans. What fraction of a pan was left?
Answers
Answer:
3/4 a pan
Step-by-step explanation:
2 - 1 1/4 = 3/4
two seperated into fourths would look like this
1/4 1/4 1/4 1/4
1/4 1/4 1/4 1/4
one seperated into fourths would look like this
1/4 1/4 1/4 1/4
so take one and one extra fourth away from two and you're left with
1/4 1/4 1/4
add that together and you have 3/4
1 peso = $ .075. How many pesos (whole number) do you get for $100 ?
Answers
Answer:
133
Step-by-step explanation:
100/.75 = 133.33 = 133